ESTIMASI RISIKO PASAR DENGAN LVaR DAN EXPECTED SHORTFALL MENGGUNAKAN SIMULASI MONTE CARLO

E-Jurnal Matematika Vol. 11(2), Mei 2022, pp. 87-93

DOI: https://doi.org/10.24843/MTK.2022.v11.i02.p365

ISSN: 2303-1751

ESTIMASI RISIKO PASAR DENGAN LVaR DAN EXPECTED SHORTFALL MENGGUNAKAN SIMULASI MONTE CARLO

I Putu Yudhi Pratama^1§ , Komang Dhamawan², Kartika Sari³

¹Program Studi Matematika, FMIPA — Universitas Udayana [Email: yudhiskater@gmail.com]

²Program Studi Matematika, FMIPA — Universitas Udayana [Email: k.dharmawan@unud.ac.id]

³Program Studi Matematika, FMIPA — Universitas Udayana [Email: ksarigerard@gmail.com]

^§Corresponding Author

ABSTRACT

Value at Risk (VaR) is a statistical technique used to manage and calculate the level of financial risk within a certain period of time and a certain level of confidence. VaR can be adjusted to liquidity risk which is called Liquidity adjusted Value at Risk (LVaR). Another alternative calculation is the Expected Shortfall (ES) which is a loss beyond the confidence limit that can occur due to liquidity. This study aims to estimate market risk with LVaR and ES on a stock portfolio incorporated in the LQ45 index using a Monte Carlo simulation. Furthermore, back-testing is carried out using the Kupiec test. The data used in this study are two stocks that are included in the LQ45 index which have the largest sales volume in a period of three years, namely ANTM and BBRI shares. As a result, it was found that the stock portfolio of ANTM and BBRI in the initial fund of Rp. 10,000,000.00 with a 95% confidence level, obtained ES of Rp.496.470,00 per day and an LVaR value of Rp 499.174,00 per day. The ES model obtained is less accurate while the LVaR model is accurate.

Keywords: Liquidity, VaR, LVaR, ES, Monte Carlo Simulation.

• 1.    PENDAHULUAN

Pasar modal (Capital Market) adalah pasar untuk berbagai instrumen keuangan jangka panjang seperti surat utang (obligasi), reksa dana, ekuiti (saham), instrumen derivatif maupun instrumen lainnya. Menurut (Sudirman, 2015) pasar modal merupakan tempat pertemuan antara pihak yang memiliki kelebihan dana (investor) dengan pihak yang membutuhkan dana dengan cara memperjualbelikan sekuritas. Tingkat pengembalian (return) yang tinggi adalah hal yang diharapkan oleh investor dalam berinvestasi. Namun investor perlu melakukan manajemen risiko karena di balik return yang tinggi terdapat risiko yang tinggi juga.

Salah satu teknik statistika yang dapat digunakan untuk mengelola dan menghitung tingkat risiko keuangan bagi perusahaan ataupun portofolio aset dalam jangka waktu tertentu adalah Value at Risk (VaR) (Damiyanti, 2018). VaR dapat digunakan untuk menghitung perkiraan kerugian maksimum yang tidak akan melampaui tingkat kepercayaan yang ditentukan selama jangka waktu yang telah ditentukan.

Pasar modal dikatakan likuid apabila penjualan dan pembelian aset dilakukan dengan cepat. Namun realitanya pasar modal tidak seratus persen likuid (Chordia, 2001). Oleh karena itu, VaR perlu disesuaikan dengan risiko likuiditas yang merupakan salah satu jenis risiko investasi. Risiko likuiditas memiliki dua bentuk, yaitu risiko likuiditas pendanaan dan risiko likuiditas aset atau pasar. Risiko likuiditas pasar muncul ketika transaksi tidak dapat dilakukan pada harga pasar yang berlaku karena ukuran posisi relatif tinggi terhadap lot perdagangan normal (Jorion, 2007).

Metode VaR yang disesuaikan dengan risiko likuiditas dinamakan Liquidity adjusted Value at Risk (LVaR) merupakan penambahan ukuran tingkat risiko likuiditas yang disebut Cost of Liquidation (COL) ke dalam model VaR (Orlova, 2008). Selain mengabaikan risiko yang diakibatkan likuiditas, VaR juga memiliki kelemahan lainnya yaitu tidak memenuhi sifat subaditif karena nilai VaR portofolio bisa saja melebihi nilai VaR saham yang dijumlahkan. Jika tidak memenuhi subaditif maka VaR tidak

memenuhi syarat koheren. Oleh karena itu, pengukuran risiko berdasarkan VaR belum tentu tepat. Untuk mengatasi masalah tersebut, maka risiko dihitung menggunakan Expected Shorfall (ES).

Artzner, et al. (1999) menunjukkan bahwa ES bersifat subaditif dengan asumsi fungsi distribusi portofolio adalah fungsi kontinu (Danielsson, 2011). ES menghitung tingkat kerugian di luar batas keyakinan yang mempertimbangkan peristiwa ekor dengan menghitung rata-rata kerugian di atas tingkat tertentu. Perhitungan ES bersifat subaditif dan koheren (Aktas, 2012).

Perhitungan VaR dan ES menggunakan simulasi Monte Carlo mensimulasikan skenario masa depan yang berdistribusi normal menggunakan pembangkitan bilangan acak yang diperoleh dari parameter distribusi return dan menggunakannya untuk mengevaluasi kembali portofolio. Metode ini mengasumsikan bahwa faktor risiko return berdistribusi normal (Madapati, 2003). Keunggulan dari simulasi Monte Carlo adalah tidak ada asumsi tentang normalitas dari return, meskipun parameter yang diestimasi berasal dari data historis (Purnamasari, 2017).

Pada index saham Indonesia terdapat index LQ45 yang memiliki tingkat likuiditas yang tinggi. Indeks LQ45 merupakan Indeks yang mengukur kinerja harga dari 45 saham yang memiliki likuiditas tinggi dan kapitalisasi pasar besar serta didukung oleh fundamental perusahaan yang baik (www.idx.co.id). Tingkat likuiditas yang tinggi pada setiap saham yang tergabung di indeks LQ45 membuat penelitian ini dilakukan untuk mengestimasi nilai risiko VaR, LVaR dan ES.

Berdasarkan uraian di atas, tujuan dari penelitian ini untuk mengetahui hasil estimasi risiko pasar dengan LVaR dan ES pada portofolio dua saham dengan likuiditas tinggi yang tergabung di indeks LQ45 dari pengaruh risiko likuiditas.

Return merupakan perubahan pada harga dari aset finansial selama jangka waktu tertentu (Danielsson, 2011). Perhitungan return dapat menggunakan rumus:

^r'=^lnG⅛) (1)

Pada metode simulasi Monte Carlo digunakan return baru yang mengikuti karakteristik return aktual saham yang diperoleh

dari pembangkitan bilangan acak. Sebelum membangkitkan bilangan acak untuk return portofolio, diperlukan parameter distribusi normal multivariat. Parameter yang dibutuhkan sebagai berikut:

• a.    Mean setiap aset

T

E(η) =⅛∑r_lιt         (2)

t = 1

• b.    Varian

T

1

^σi =γ-[∑[^rit^-E(rit)]2(3)

t = 1

• c.    Kovarian

1

^σij = f-ι∑{[^ri-t ^{- E}(^ri,t^)][rj,t(4)

t = 1

^-E(rj,t)^])

• d.    Korelasi antar aset

  Pxy =

  
  

  ^σχγ

  ^σχ^σγ

  
  

  (5)

  
  

• e.    Matriks Varian-Kovarian

Iσ11

σ21

^σN1■"

^σ1W^l . I ^σNNj

(6)

Parameter yang diperoleh digunakan untuk membangkitkan bilangan acak. Setelah itu dapat dihitung return portofolio sebagai berikut:

R_p = w₁r₁ + w₂r₂ +-----+ w_Nr_N

= [^w1  ^w2      W_n]∖ 2

(7)

VaR merupakan metode pengukuran risiko. Secara umum VaR merupakan kemungkinan terburuk yang terjadi pada suatu periode yang nilainya tidak akan melampaui pada suatu tingkat kepercayaan tertentu (Jorion, 2007). Nilai VaR dengan tingkat kepercayaan (1 — α) dengan periode t dirumuskan sebagai:

VaR(₁-_α>(Δt) = W₀R* √t

(8)

Expected Shortfall adalah kerugian yang diharapkan melebihi kerugian VaR (Danielsson, 2011):

ES = -E[Q∣Q ≤ -VaR(p)]    (9)

denagn Q merupakan profit dan kerugian dalam VaR. dan VaR (p) merupakan perhitungan VaR pada probabilitas p.

Setelah perhitungan VaR dan ES, dapat dihitung nilai risiko likuiditas portofolio. Risiko likuiditas dapat dihitung dengan mencari nilai bid-ask spread portofolio (Hull, 2018) menggunakan rumus berikut:

Ask Price — Bid Price Mid — market Price

(10)

Dari hasil perhitungan bid-ask spread, selanjutnya dapat dihitung nilai Cost of Liquidation (COL) dengan rumus berikut:

n

Σ SilZi     ,  ,

(11)

i=1

dengan Si adalah perkiraan dari proporsional bid-ask spread dalam kondisi pasar normal untuk instrumen keuangan ke-i yang dipegang

oleh lembaga keuangan dan ai adalah nilai aset

dari posisi di instrumen keuangan ke-i. dan 'n adalah jumlah posisi.

VaR dapat disesuiakan dengan risiko

likuiditas yang disebut LVaR dengan

penjumlahan VaR dan COL (Hull, 2018). LVaR

dapat dirumuskan sebagai berikut: n

^ ^si^ai i=i

LVaR = VaR +

(12)

Setiap model risiko perlu dicek keakuratannya dengan uji validasi atau backtesting. Back-testing pada penelitian ini menggunakan Uji Kupiec dengan rumus sebagai berikut:

LLR = —2ln[(1 — p)^T-Np^N]

+ 2^-(⅛^ ⁽1³⁾

dengan p adalah tingkat signifikansi, N adalah jumlah kegagalan (failures) dan T adalah jumlah sampel. hipotesis nol dari Uji Kupiec adalah model perhitungan VaR baik atau akurat. LR secara asimtotik berdistribusi χ² dengan derajat bebas 1. Jika nilai statistik LR melebihi daerah kritis dan dari distribusi chi-square maka H₀ ditolak yang artinya perhitungan VaR tidak valid.

• 2.    METODE PENELITIAN

Jenis data yang digunakan merupakan jenis data sekunder yang diperoleh dari website yahoofinance.com berupa data kuantitatif yaitu harga penutupan saham harian dari 1 Januari 2018 - 4 Januari 2021. Data saham yang

digunakan adalah dua saham yang dipilih dengan acuan volume penjualan tertinggi dalam enam bulan dari Januari - Juni 2021 di indeks LQ45. Adapun langkah-langkah penelitian ini yaitu:

• 1.    Memilih 2 saham yang tergabung dalam indeks LQ45 dengan acuan volume penjualan terbesar.

• 2.    Menghitung log return harian dari masing-masing saham yang diperoleh di langkah (1) menggunakan persamaan (1) dengan bantuan softwere Matlab.

• 3.    Menentukan nilai parameter beserta korelasi sesuai distribusi return aset pembentuk portofolio untuk pembangkitan bilangan acak. Dengan distirbusi return aset pembentuk portofolio merupakan distribusi normal multivariat sehingga parameter yang dibutuhkan yaitu:

• a.    Menghitung expected return (μ) menggunakan persamaan (2).

• b.    Menghitung varian   menggunakan

persamaan (3).

• c.    Menghitung  kovarian  menggunakan

persamaan (4).

• d.    Menghitung korelasi antar aset menggunakan persamaan (5).

• e.    Membentuk matriks varian-kovarian menggunakan persamaan (6).

• 4.    Mensimulasikan      return      dengan

membangkitkan bilangan acak sesuai parameter yang diperoleh di langkah (3) sebanyak n buah dengan bantuan software matlab R2016b.

• 5.    Nilai return masing-masing aset yang diperoleh pada langkah (4) digunakan untuk menghitung return portofolio menggunakan persamaan (7).

• 6.    Mengestimasi nilai kerugian maksimum pada tingkat kepercayaan (1 — a) yaitu sebagai nilai kuantil ke - a dari distribusi empiris return portofolio yang diperoleh pada langkah (5).

• 7.    Menghitung nilai VaR pada tingkat kepercayaan (1 — a) dalam periode waktu t menggunakan persamaan (8).

• 8.    Menghitung nilai ES dari return yang melebihi kerugian dari kuantil  ke-a

menggunakan persamaan (9).

• 9.    Mengulangi langkah (4) sampai langkah (8) sebanyak m₁ = 100, m2 = 1000, dan m₃ = 10000 sehingga mendapatkan berbagai kemungkinan nilai VaR dan ES portofolio yaitu       VaR₁, VaR₂...., VaR_jn       dan

  ES1,ES2,.

  
  

  ,ES

  
  

  n^.

  
  

• 10.    Menghitung rata-rata hasil nilai dari langkah (9) untuk menstabilkan nilai VaR dan ES yang diperoleh dari tiap simulasi karena memiliki nilai yang berbeda.

• 11.    Menghitung nilai bid-ask spread portofolio saham guna mencari nilai Cost of Liquidation (COL) untuk perhitungan LVaR menggunakan rumus pada persamaan (10).

• 12.    Menghitung COL pada portofolio untuk mengetahui risiko akibat dari likuiditas dengan menggunakan rumus pada persamaan (11)

• 13.    Mengestimasi nilai LVaR pada portofolio menggunakan persamaan (12)

• 14. Setelah mendapatkan perhitungan LVaR dan ES, akan dilakukan back-testing untuk mengecek akurasi perhitungan kerugian model dengan kerugian aktual menggunakan Uji Kupiec pada persamaan (13).

• 15.I nterpretasi hasil penelitian.

• 3.    HASIL DAN PEMBAHASAN

Data yang digunakan pada penelitian ini adalah dua saham dengan volume penjualan tertinggi selama 6 (enam) bulan pada Januari – Juni 2021. Dua saham dengan volume penjualan tertinggi tersebut adalah saham PT Aneka Tambang Tbk (ANTM) dengan jumlah volume penjualan sebesar 30.791.772.400 lot dan saham PT Bank Rakyat Indonesia Tbk (BBRI) dengan jumlah volume penjualan sebesar 14.501.640.600 lot.

Selanjutnya menghitung nilai log return setiap saham pembentuk portofolio dengan data harga penutupan masing-masing saham menggunakan persamaan (1) pada periode 1 Januari 2018 – 4 Januari 2021.

Setelah mendapatkan nilai log return setiap saham, dihitung parameter portofolio saham untuk menghitung return baru masing-masing saham dengan membangkitkan bilangan acak.

• 3.1    Menghitung Parameter untuk

Pembangkitan Bilangan Acak

Pertama-tama parameter yang dihitung yaitu nilai expected return saham ANTM dan BBRI dari nilai log return menggunakan persamaan (2). Secara berturut-turut nilai expected return saham ANTM dan BBRI adalah 0,0016 dan 0,00002231.

Setelah mendapatkan nilai expected return, dihitung nilai varian saham portofolio dengan persamaan (3). Hasil perhitungan varian saham ANTM dan BBRI secara berturut-turut adalah 0.00106044 dan 0.00567.

Selanjutnya dihitung nilai kovarian portofolio saham, Berdasarkan varian saham yang    diperoleh sebelumnya dengan

menggunakan persamaan (4) diperoleh nilai kovarian portofolio yaitu

• ^oANTM BBRI = 0.⁰⁰⁰⁷⁷8 karena  o^awtm bbri = ^obbri antm ^, sehingga

diperoleh nilai Obbri awtm = °antm bbri yaitu ^c⅛_{br1 a}w_tm = 0.000778. Nilai Kovarian yang positif menandakan return saham ANTM dan BBRI cenderung bergerak beriringan.

Selanjutnya dapat dihitung nilai korelasi antar saham menggunakan persamaan (5), diperoleh nilai korelasi antar saham ANTM dan BBRI yaitu

Pantm bbri = 0.4⁰⁸⁴

nilai korelasi yang positif menandakan bahwa saham ANTM dan BBRI ada hubungan keterkaitan dalam pergerakan return yang cenderung searah.

Setelah diperoleh nilai parameter dan korelasi, dapat dibentuk matriks varian-kovarian menggunakan persamaan (6) sebagai berikut:

_{y =} Γ0.0010604  0.00003171

∑   [0.0000317   0.00567 ]

Setelah memperoleh parameter μ dan ∑, dihitung return baru dari membangkitkan bilangan acak menggunakan bilangan acak normal multivariat dengan μ dan ∑ yang telah diperoleh sebelumnya. Simulasi dilakukan dengan bantuan software Matlab R2016b. Return baru yang dibangkitkan sebanyak n = 760 dengan n adalah return ke-n saham sehingga terbentuk distribusi empiris dari return yang dihasilkan dari simulasi.

Setelah mendapatkan return baru dari hasil pembangkitan bilangan acak, dihitung return portofolio saham dengan bobot masing masing saham w = 0,5 . Perhitungan return portofolio saham menggunakan persamaan (7).

• 3.2    Menghitung Risiko Pasar dengan VaR dan ES

Setelah mendapatkan return baru portofolio dari hasil pembangkitan bilangan acak, selanjutnya return diurut dari nilai terkecil ke nilai terbesar untuk mencari nilai kuantil ke-a. Nilai kuantil yang diperoleh dinotasikan R* sebagai kerugian maksimum harian. Sebagai contoh R* simulasi pertama dengan a = 5%, diperoleh yaitu sebesar R* = -3,99%.

Setelah diperoleh kerugian maksimum dari nilai kuantil ke-a, dihitung kerugian portofolio pada perhitungan VaR. VaR dihitung menggunakan persamaan (8). Dengan dana awal investasi portofolio saham Rp. 10.000.000, diperoleh nilai VaR simulasi pertama sebagai berikut:

VaR(ι-ou₅)(1) = V √i

VaR(₀.95)(1) = 10.0 0 0.0 0 0 × -3,99%√1 VaR₍₀.₉₅₎(1) = 10.0 0 0.0 0 0 × -3,99% VaR(o.9₅)(1) = -39 9.0 0 0

Karena VaR merupakan bilangan positif sehingga nilai VaR₁ = 399.000. nilai VaR₁ ini menjelaskan bahwa kerugian portofolio saham dalam satu hari perdagangan tidak akan melebihi Rp.399.000.

Setelah mendapatkan VaR, dapat dihitung nilai ES dengan menghitung rata-rata dari kuantil yang melebihi nilai VaR atau kerugian terburuk yang melebihi nilai VaR. Dengan menggunakan persamaan (9) nilai ES portofolio saham pada simulasi pertama dengan dana awal portofolio saham sebesar Kk₀ = Rp. 10.000.000 diperoleh ES₁ = 479.900 yang artinya portofolio saham memiliki potensi kerugian yang melebihi kerugian maksimal sebesar Rp. 479.900 dalam seharai diakibatkan oleh kerugian yang tidak terduga.

Pada pehitungan sebelumnya telah diperoleh nilai VaR dan ES dari simulasi pertama, dikarenakan return diperoleh dengan pembangkitan bilangan acak sehingga perlu dilakukan simulasi ulang untuk mendapatkan berbagai kemungkinan nilai VaR dan ES. Selanjutnya dilakukan pengulangan simulasi. Pada penelitian ini digunakan tiga skenario simulasi dengan jumlah simulasi yang digunakan      yaitu      m₁ = 100, m2 =

1000 dan m3 = 10000.

Setelah mendapatkan seluruh nilai VaR dan ES yang dihasilkan setiap simulasi dirata-ratakan untuk menstabilkan nilai VaR dan ES dikarenakan hasil setiap simulasi berbeda.

VaR_mi

VaR1 + VaR2 + ∙∙∙ + VaR100

100

-3,84611

100

= -0,038461

VaR_mi(1) = 10.000.000 × -3,8461%√1

VaR_mi (1) = -384.610

dan

_ ^ES1 ⁺ ES2 ⁺ '" ⁺ ES100

^mi =        100

= -0,049647

= 10.000.000 × -4,9647%√1

ES_mι(1) = -496.470

Karena nilai VaR dan ES merupakan bilangan positif sehingga VaR = 384.610 dan ES = 496.470 yang artinya portofolio saham memiliki potensi kerugian maksimal sebesar Rp.384.610 perhari pada tingkat kepercayaan 95% dan portofolio saham memiliki potensi kerugian yang melebihi kerugian maksimal sebesar Rp.496.470 pada tingkat signifikan 5% yang diakibatkan oleh kerugian tidak terduga. Dengan cara yang sama dihitung rata-rata VaR dan rata-rata ES pada skenario m2 = 1000 dan m3 = 10000. Secara berturut-turut diperoleh VaR_m = 380.000 dan   ES_m = 497.000

sedangkan VaR_m = 380.000  dan ES_m =

497.000 .

• 3.3    Menghitung LVaR

Sebelum menghitung nilai LVaR, perlu dihitung biaya untuk melikuidasi aset yaitu nilai Cost of Liquidation (COL) yang diperoleh dari perhitungan nilai bid-ask spread. Bid-ask spread digunakan untuk mengukur tingkat likuiditas suatu aset dihitung menggunakan persamaan (1010).

Selanjutnya dapat dihitung nilai COL harian portofolio menggunakan persamaan (11). Setelah diperoleh nilai COL harian portofolio saham pada periode 1 Januari 2018 – 4 Januari 2021, dihitung rata-rata COL harian portofolio saham sebagai berikut:

'∙'^ul rata-rata

COL1 + ••• + COL760

760

C∩I. . rata-rata

COLrata-rata

90.572.285,11

=    760

= 119174,06

Sehingga diperoleh nilai COL_rata-_rata = Rp. 119.174,06 yang artinya investor perlu menyediakan biaya rata-rata melikuidasi portofolio saham per hari sebesar Rp. 119.174,06 untuk mengantisipasi risiko likuiditas portofolio.

LVaR merupakan ukuran risiko dengan penambahan risiko likuiditas pada suatu aset atau nilai VaR yang dijumlahkan dengan COL pada suatu aset. Perhitungan LVaR portofolio saham menggunakan persamaan (12) sebagai berikut:

LVaR = VaR + COL

1^1

= 384.610 + 119.174,06

LVaR_mi = 503.784

Pada skenario m₁ diperoleh nilai VaR yang disesuaikan dengan risiko likuiditas sebesar Rp. 503.784 yang artinya dalam sehari portofolio saham memiliki potensi kerugian maksimal dengan biaya melikuidasi aset sebesar Rp. 503.784 pada tingkat kepercayaan 95%. Dengan cara yang sama dihitung LVaR pada skenario m2 = 1000 dan m₃ = 10000. Secara berturut-turut diperoleh LVaR_m2 Rp. 499.174 dan LVaR_m Rp.499.174.

• 3.4    Back-testing Model Risiko

Sebelumnya, telah dihitung nilai risiko VaR, ES dan LVaR. Selanjutnya setiap model risiko perlu dilakukan back-testing untuk mengecek keakuratan model risiko atau validasi model. Dicari return aktual yang melebihi nilai dari setiap model atau disebut pelanggaran hari.

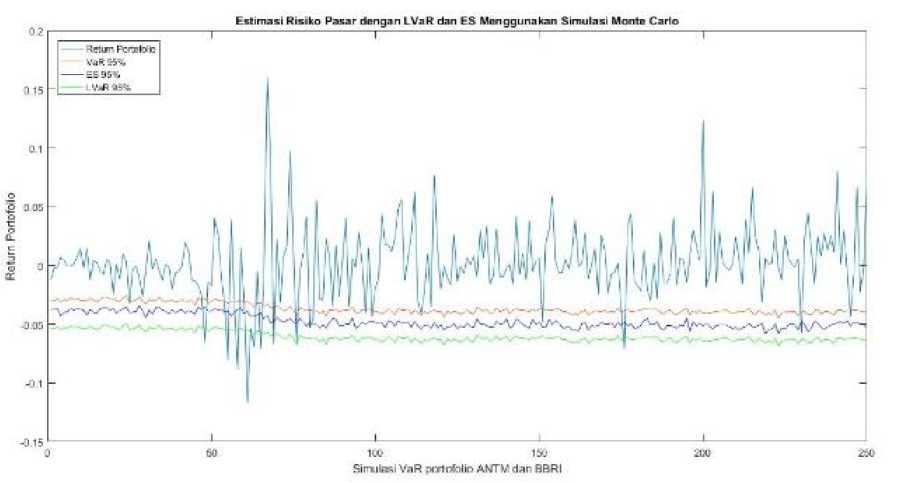
Gambar 1. Pelanggaran Hari Return Aktual yang Melebihi Nilai VaR, ES dan LVaR.

Dapat dilihat dari Gambar 1. Garis biru bagian atas menunjukkan return portofolio saham ANTM dan BBRI yang dignakan untuk mengecek validasi model. Selanjutnya garis merah menunjukkan nilai VaR dengan tingkat kepercayaan 95%, garis biru pada bagian bawah menunjukkan nilai ES dengan tingkat kepercayaan 95%, dan garis hijau menunjukkan LVaR dengan tingkat kepercayaan 95%. Dari Gambar 1. diketahui bahwa terdapat return portofolio saham yang melebihi model risiko. Terdapat 19 hari pelanggaran untuk return portofolio yang melebihi VaR 95% , 12 hari pelanggaran untuk return portofolio yang

melebihi ES 95%, dan sembilan hari pelanggaran untuk return portofolio yang melebihi LVaR 95%.

Dari pelanggaran hari  yang diperoleh

dilakukan uji statistik dengan Uji Kupiec untuk mengetahui model risiko akurat atau tidak menggunakan persamaan (13). Dengan tingkat probabilitas p = 5% diperoleh nilai Likelihood Rasio (LR) VaR dan ES secara berturut-turut adalah LR = 1,90571 dengan p — value = 0,17 dan LR = 9,2822dengan  p — value =

0,002.

Nilai LR dibandingkan dengan chi-square dengan derajat kebebasan sebesar 1 (satu)

untuk tingkat kepercayaan model risiko. Nilai chi-square untuk tingkat kepercayaan 95% adalah 3,84.

Hasil back-testing diketahui bahwa VaR akurat sedangkan ES tidak akurat. Sedangkan LVaR akurat karena LVaR menggunakan dasar model VaR dengan model VaR yang sudah akurat sehingga tidak mengharuskan model LVaR untuk melakukan back-testing lagi.

• 4.    KESIMPULAN DAN SARAN

Pada penelitian ini, saham pembentuk portofolio dipilih dua saham dengan volume penjualan saham tertinggi selama bulan Januari - Juni 2021 pada indeks LQ45 yaitu saham ANTM dan BBRI. Perhitungan risiko pasar dalam penelitian ini menggunakan metode Simulasi Monte Carlo. Pada dana awal Rp.10.000.000 dengan tingkat kepercayaan 95% diperoleh VaR sebesar Rp. Rp.380.000, ES sebesar Rp.497.000, dan LVaR sebesar Rp.499.174 dalam satu hari perdagangan. Hal ini mengindikasikan risiko maksimal harian portofolio dengan adanya risiko likuiditas sebesar Rp.499.174 dan kerugian yang diharapkan di luar batas tingkat kepercayaan sebesar Rp.497.000. Setelah mendapatkan nilai risiko setiap model, perlu dilakukan validasi model atau back-testing. Pada penelitian ini back-testing menggunakan Uji Kupiec dengan pendekatan loglikelihood ratio. Hasil yang diperoleh ES tidak akurat dengan jumlah pelanggaran 12 hari dan LVaR akurat dikarekan model VaR yang akurat dengan jumlah pelanggaran LVaR 9 hari. Untuk itu, investor dapat menggunakan LVaR dalam mengukur risiko pasar pada portofolio dengan adanya penyesuaian likuiditas.

Untuk penelitian selanjutnya, penulis menyarankan untuk menggunakan penyesuaian likuiditas ke model risiko lainnya seperti VaR yang diestimasi dengan metode selain simulasi monte carlo atau penyesuaian likuiditas ke model ES.

DAFTAR PUSTAKA

Aktas, C., Cortuk, O., Teker, S., & Yildirim, B.

D. 2012. Measurement of Liquidity-Adjusted Market Risk by VaR and Expected Shortfall: Evidence from Turkish Banks. Journal of Applied Finance and Banking. Vol. 2. No. 5. 137-147.

Chordia, T., Roll, R., & Subrahmanyam, A. 2001. Market Liquidity and Trading Activity. The Journal of Finance. Vol LVI. No. 2. 501-530.

Danielsson, J. 2011. Financial Risk Forecasting: The Theory and Practice of Forecasting    Market Risk    with

Implementation in R and Matlab. John Wiley & Sons. United Kingdom.

Damiyanti,D.P.D., Dharmawan, K., Harini, L.P.I. 2018. Perhitungan Value at Risk dengan Penduga Volatilitas Stokastik Heston. E-Jurnal Matematika Universitas Udayana. Vol. 7(4). 317-318.

Hull, J. 2018. Risk Management and Financial Institutions. John Wiley & Sons. Hokoben, New Jersey.

Jorion, P. 2007. Value at Risk: The New Benchmark for Managing Financial Risk. The McGraw-Hill Companies, Inc.. United States of America.

Orlova, E. 2008. Estimation of Liquidity-Adjusted VaR from Historical Data (Master's thesis, Humboldt-Universität zu Berlin,      Wirtschaftswissenschaftliche

Fakultät).

Purnamasari, N. A. 2017. Backtesting untuk Value at Risk Pada Return Saham Bank Syariah     Menggunakan     Quantile

Regression.. Tesis.  Institut  Teknologi

Sepuluh Nopember, Program Magister

Jurusan Statistika Fakultas Matematika dan Ilmu Pengetahuan Alam, Surabaya

Sudirman. 2015. Pasar Modal dan Manajemen Portofolio. Sultan Amai Press IAIN Sultan Amai Gorontalo. Gorontalo.

93