PENENTUAN KEPUTUSAN INVESTASI SAHAM MENGGUNAKAN CAPITAL ASSET PRICING MODEL (CAPM) DENGAN PENAKSIR PARAMETER STOKASTIK
on
E-Jurnal Matematika Vol. 10(4), November 2021, pp. 251-257
DOI: https://doi.org/10.24843/MTK.2021.v10.i04.p351
ISSN: 2303-1751
PENENTUAN KEPUTUSAN INVESTASI SAHAM MENGGUNAKAN CAPITAL ASSET PRICING MODEL (CAPM) DENGAN PENAKSIR PARAMETER STOKASTIK
Icha Winda Dian Safira1§, Komang Dharmawan2, Desak Putu Eka Nilakusmawati3
1Program Studi Matematika, FMIPA, Universitas Udayana [Email: ichawindadiansafira@gmail.com] 2Program Studi Matematika, FMIPA, Universitas Udayana [Email: k.dharmawan@unud.ac,id] 3Program Studi Matematika, FMIPA – Universitas Udayana [Email: nilakusmawati@unud.ac.id]
§Corresponding Author
ABSTRACT
CAPM is a method of determining efficient or inefficient stocks based on the differences between individual returns and expected returns based on the CAPM’s positive value for efficient and negative value for inefficient stocks. The move to share prices in the process can influence investors's decisions in investing funds, so that it can be formulated in stochastic differential equations that form the Geometric Brownian Motion model (GBM). The purpose of the study is to determine return value using the CAPM based on share estimates and historical stock prices. The study uses secondary data that data a monthly closing of stock prices from December 2017 to December 2020. The GBG model's estimated stock price is used to determine the expected value return using the CAPM. In this case, it is called CAPM-Stochastic. Then the results of the CAPM-Stochastic was compared to the results of the CAPM-Historical to define efficient stocks and inefficient stocks. The results of research using CAPM-Stochastic obtained that HMSP, ICBP, KLBF, and WOOD shares are efficient stock while UNVR shares are inefficient. The results of CAPM-Historical obtained that HMSP, ICBP, KLBF, and UNVR shares are inefficient stocks and WOOD is an efficient stocks.
Keywords: Geometric Brownian Motion, CAPM-Stochastic, Efficient Stock
Dunia investasi di Indonesia akhir-akhir ini mulai banyak dilirik oleh masyarakat dari berbagai kalangan, tidak hanya dari kalangan investor tetapi juga banyak menarik perhatian kalangan masyarakat dan generasi muda zaman sekarang. Salah satu jenis instrumen keuangan yang paling banyak diperdagangkan di pasar modal adalah saham. Dalam kegiatan investasi, pergerakan harga saham ditandai oleh adanya indeks harga saham. Salah satu indeks harga saham di Indonesia adalah indeks Sektor Industri Barang Konsumsi.
Investasi saham pada pasar modal untuk memperoleh tingkat pengembalian (return). Dalam berinvestasi investor mengusahakan agar memperoleh tingkat pengembalian terbesar dengan risiko tertentu. Sehingga dalam berinvestasi saham pada pasar modal, investor diharapkan dapat menentukan keputusan investasi sesuai dengan profil risikonya untuk meminimalkan risiko yang akan diperoleh.
Oleh karena itu, diperlukan model keseimbangan untuk menentukan hubungan antara risiko dan tingkat pengembalian yang diharapkan untuk setiap aset dalam keadaan pasar yang seimbang. Model tersebut adalah capital asset pricing model (CAPM). CAPM dapat digunakan untuk menentukan saham-saham efisien pada suatu sekuritas berdasarkan tingkat pengembalian yang diharapkan lebih kecil dari tingkat pengembalian saham individu (Tandelilin, 2017). Risiko dalam CAPM diukur oleh variabel yang disebut beta (β).
Penelitian terdahulu yang menggunakan CAPM dalam menentukan saham efisien yaitu pada penelitian Liadi, dkk. (2020) dan Haidiati, dkk. (2016). Kedua penelitian tersebut menggunakan CAPM dengan perhitungan beta langsung menggunakan data harga saham historis. Ameliah dkk. (2017) membandingkan perhitungan risiko (beta) dengan CAPM dengan perhitungan beta diestimasi menggunakan GARCH dan EGARCH.
Sedangkan penelitian ini akan menentukan CAPM berdasarkan data harga saham yang diestimasi terlebih dahulu.
Fluktuasi harga saham yang selalu berubah dapat memengaruhi keputusan investor dalam menginvestasikan dananya. Pergerakan harga saham tersebut mengikuti proses stokastik sehingga dapat dirumuskan dalam persamaan diferensial stokastik. Berdasarkan Yunita dkk. (2015), persamaan diferensial stokastik disajikan dalam model matematis untuk mengestimasi harga saham yang akan membentuk suatu model dinamakan Gerak Brown Geometri (GBG). Model GBG digunakan karena model ini sesuai untuk mengestimasi harga saham pada masa yang akan datang dalam investasi (Abidin dan Jaffar, 2014).
Pada penelitian ini perolehan harga saham yang telah diestimasi menggunakan GBG menjadi bahan kajian selanjutnya dalam menentukan CAPM. Kemudian, hasil yang diperoleh akan dibandingkan berdasarkan hasil perhitungan CAPM menggunakan GBG dan CAPM menggunakan data historis.
Husnan (2015), menentukan persamaan CAPM untuk menghitung tingkat pengembalian yang diharapkan dari suatu sekuritas adalah sebagai berikut:
E(rl) = τf + (e(tm) - rf}βi (1)
dengan E(rl) adalah tingkat pengembalian yang diharapkan dari saham ke-i, Tf adalah tingkat pengembalian bebas risiko, E(tm) adalah tingkat pengembalian indeks pasar, dan βl adalah risiko dari saham ke-i. Berikut ini adalah cara untuk mengukur beta dari suatu saham:
„ Et=i(ri-fl).(,rM -rM))
βl = ∑T=ι(rM-fM)2 (2)
Mengacu pada Dmouj (2006), model GBG dapat ditentukan sebagai berikut:
dSt = μStdt + σStdWs (3)
dengan St adalah harga saham pada saat t, μ adalah ekspektasi return saham, σ adalah standar deviasi dari return saham dan Ws adalah Gerak Brown yang dimulai pada W0 = 0.
Pada ruas kanan persamaan (3) adalah proses Gerak Brown yang merupakan unsur stokastik sehingga untuk menyelesaikan persamaan (3) digunakan penerapan dari Lemma Ito, fungsi G = G(S, t) yaitu:
dG = (^‘ + T.+-^-^ + ∂G-σSldW,(4)
∂j t
Dari Lemma Ito, fungsi G = G(S, t) pada persamaan (4) akan diperoleh:
St = St-1exp[(μ-1σ-)∆t + σdWs](5)
Sehingga dapat dinyatakan bahwa harga saham pada masa depan mengikuti model GBG seperti pada persamaan (5).
-
2. METODE PENELITIAN
Data yang digunakan adalah data penutupan harga saham bulanan pada perusahaan di sektor industri barang konsumsi periode Desember 2017 hingga Desember 2020. Perusahaan-perusahan yang akan diteliti berada di kelima subsektor tersebut, yaitu PT. Indofood CBP Sukses Makmur Tbk. (ICBP), PT. H.M. Sampoerna Tbk. (HMSP), PT. Kalbe Farma Tbk. (KLBF), PT. Unilever Indonesia Tbk. (UNVR), dan PT. Integra Indocabinet Tbk. (WOOD).
Langkah-langkah yang digunakan dalam penelitian ini adalah:
-
1. Mengumpulkan data harga saham bulanan pada masing-masing saham periode Desember 2017 hingga Desember 2020.
-
2. Menghitung tingkat pengembalian (return) dari masing-masing saham.
-
3. Menentukan CAPM menggunakan GBG pada masing-masing saham.
-
a. Melakukan estimasi harga saham terhadap masing-masing saham menggunakan model GBG.
-
b. Menghitung tingkat pengembalian (return) pada masing-masing saham berdasarkan perolehan data harga saham estimasi menggunakan model GBG.
-
c. Menghitung tingkat pengembalian pasar.
-
d. Menghitung beta masing-masing saham dengan CAPM setelah memperoleh hasil return berdasarkan perolehan harga saham estimasi.
-
e. Menentukan tingkat pengembalian yang diharapkan dari masing-masing saham berdasarkan CAPM
menggunakan GBG.
-
4. Menentukan CAPM pada masing-masing saham menggunakan data historis.
-
5. Membandingkan hasil perhitungan tingkat pengembalian yang diharapkan dari CAPM menggunakan GBG dan CAPM
menggunakan data historis.
-
3. HASIL DAN PEMBAHASAN
Berdasarkan Gambar 1 harga saham HMSP dan UNVR mengalami penurunan yang signifikan hingga akhir periode. Kemudian harga saham ICBP dan KLBF cenderung datar dengan fluktuatif. Sedangkan harga saham WOOD mengalami fluktuasi yang signifikan pada seluruh periode.
-
3.2 Menentukan Nilai Return Pada Masing-masing Saham
Perhitungan nilai return pada masing-masing saham, sebagai contoh pada saham
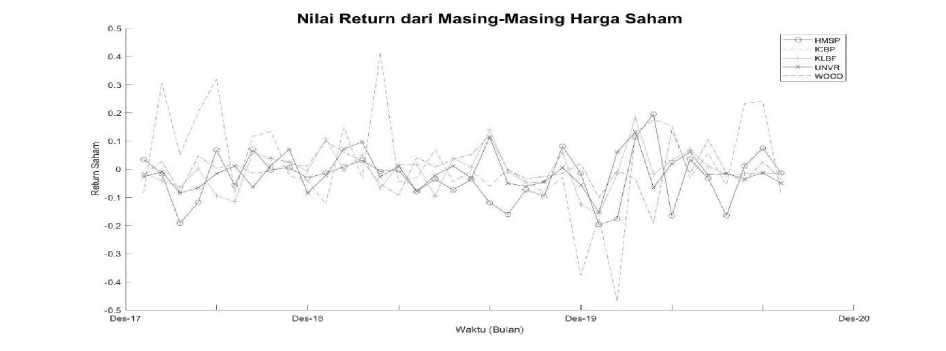
Gambar 2. Nilai Return Saham HMSP, ICBP, KLBF, UNVR, dan WOOD
Pada Gambar 2 dapat dilihat bahwa return saham HMSP, ICBP, KLBF, dan UNVR cenderung mengalami fluktuasi yang naik turun hingga akhir periode. Return saham WOOD pada Bulan Januari hingga April 2020 mengalami fluktuasi naik turun yang cukup signifikan.
ICBP harga saham pada bulan Januari 2018 adalah Rp 8900 dan bulan Desember 2017 adalah Rp 8725 maka tingkat pengembalian (return) saham ICBP adalah:
8900∖
rι = l"fe) r1 = -0,01986
Nilai r1 = -0,01986 menunjukkan bahwa return saham mengalami penurunan sebesar 1,986% dibandingkan dengan sebelumnya.
Nilai return dapat disajikan pada Gambar 2.
Dalam proses estimasi harga saham, data yang digunakan adalah data harga penutupan saham bulanan dari Bulan Desember 2017 hingga Desember 2020 dalam menentukan parameter untuk membangun model simulasi harga saham.
-
3.3.1 Menentukan Parameter dalam Model Gerak Brown Geometri
Dalam bentuk model estimasi harga saham terdapat dua parameter yaitu parameter μ dan parameter σ. Hasil perhitungan parameter dalam membangun model GBG disampaikan pada Tabel 1.
Tabel 1. Estimasi Parameter dalam Model GBG
|
Saham |
μ |
σ |
|
HMSP |
-0,0318 |
0,0910 |
|
ICBP |
0,0020 |
0,0635 |
|
KLBF |
-0,0037 |
0,0702 |
|
UNVR |
-0,0117 |
0,0608 |
|
WOOD |
0,0231 |
0,1764 |
-
3.3.2 Estimasi Harga Saham Menggunakan Model Gerak Brown Geometri
Setelah diperoleh nilai parameter pada uraian sebelumnya, kemudian langkah selanjutnya adalah menyubstitusikan nilai parameter tersebut ke dalam model GBG dengan dengan ∆t = 1/242 merupakan periode untuk mengestimasi harga selama 242 hari dalam satu tahun dan harga saham awal menggunakan data harga Bulan Desember 2020 yang disajikan pada Tabel 2.
Harga yang diestimasi dengan periode 242 hari selama satu tahun pada setiap saham menghasilkan 242 harga yang diubah ke bulanan dengan mengambil harga pada akhir bulan. Sehingga terdapat 12 harga saham bulanan pada setiap saham.
Tabel 2. Model Estimasi Harga Saham dengan Gerak Brown Geometri
|
No. |
Saham |
Model Estimasi Harga Saham dengan Gerak Brown Geometri | ||
|
1. |
HMSP |
St = (1505)exp |
(-W318^0,0910)2)^^^ | |
|
2. |
ICBP |
St= (9575) exp |
(0,0020 -1 (0,0635)2)(^) + (0,0635)ε J^ | |
|
3. |
KLBF |
St = (1480)exp |
(-0,0037-∣(M702)2)(242) + ^^^ | |
|
4. |
UNVR |
St = (7350)exp |
(-°,0117- !(O,0608)2^) + (0,0608)eJΣ | |
|
5. |
WOOD |
St = (560)exp |
(0,0231-2(0,l764)∙)(242) + (0Λ764)≈J242 | |
-
3.4 Menentukan Capital Asset Pricing
Model (CAPM)
Setelah memperoleh data harga saham bulanan pada masing-masing saham yaitu data harga saham estimasi dan data harga saham historis selanjutnya data harga saham-saham tersebut digunakan untuk menentukan CAPM-Stokastik dan CAPM-Historis.
-
3.4.1 Return Berdasarkan Harga Saham Estimasi
Hasil perhitungan return berdasarkan harga saham estimasi diperoleh bahwa nilai rata-rata return saham HMSP adalah -0,00297, ICBP adalah -0,00007, KLBF adalah -0,00057, UNVR adalah -0,00091, dan WOOD adalah 0,00203. Dari kelima saham tersebut nilai rata-rata return tertinggi dimiliki oleh saham
WOOD dan nilai rata-rata return terendah dimiliki oleh saham HMSP.
-
3.4.2 Return Berdasarkan Harga Saham
Historis
Hasil perhitungan return berdasarkan harga saham historis diperoleh bahwa nilai rata-rata return saham HMSP adalah -0,03181, ICBP adalah 0,00203, KLBF adalah -0,00369, UNVR adalah -0,01165, dan WOOD adalah 0,02308. Dari kelima saham tersebut nilai rata-rata return tertinggi dimiliki oleh saham WOOD dan nilai rata-rata return terendah dimiliki oleh saham HMSP.
-
3.4.3 Nilai Return Pasar Historis dan Pasar Estimasi
Berdasarkan perhitungan diperoleh nilai rata-rata tingkat pengembalian pasar historis
(E(RmJ) sebesar -0,00047 dan nilai rata-rata tingkat pengembalian pasar estimasi (E(Rm)) sebesar -0,00022.
Beta merupakan suatu pengukur volatilitas return suatu sekuritas terhadap return pasar. Hasil perhitungan nilai beta CAPM-Stokastik dan beta CAPM-Historis dapat dilihat pada Tabel 3. Salah satu contoh proses perhitungan nilai Beta (βi) CAPM-Stokastik pada saham HMSP adalah sebagai berikut:
_ ∑t=ι(ri - rl).(rM - Γm))
‘ ∑t=ι(rM-rM)2
((0,00017- (-0,0029 7).(0,00148- (-0,00022))+■ +
„ ((-0,00663- (-0,00297).(-0,00222-(-0,00022))
βi = (0,00148- (-0,00022))2 + ∙ +
(-0,00222- (-0,00 022))2
(0,00314).(0,0017)+ ■+ ((-0,00366).(-0,00199))
?i = (0,0017)2+ •••+ (-0,00199)2
0,00003108
β = 0,00001635
βf =1,90030
Tabel 3. Hasil Perhitungan Beta CAPM-Stokastik dan CAPM-Historis Pada Masing-masing Saham
|
Saham |
Beta CAPM-Stokastik |
Beta CAPM-Historis |
|
HMSP |
1,90030 |
1,18075 |
|
ICBP |
1,29882 |
0,20786 |
|
KLBF |
1,44293 |
0,67198 |
|
UNVR |
0,38044 |
0,27375 |
|
WOOD |
1,05731 |
1,67418 |
Pada Tabel 3 perhitungan beta berdasarkan CAPM-Stokastik pada saham HMSP, ICBP, KLBF, dan WOOD memiliki nilai beta lebih besar dari satu sedangkan pada CAPM-Historis dimiliki oleh saham HMSP dan WOOD, artinya saham tersebut berisiko lebih besar dari risiko pasar. Begitu juga jika memiliki nilai beta lebih kecil dari satu, maka saham tersebut berisiko lebih kecil dari risiko pasar.
Variabel yang memenuhi pada persamaan CAPM adalah tingkat pengembalian yang diharapkan dari saham ke-i (E(ri)), tingkat pengembalian bebas risiko (rz) menggunakan suku bunga Bank Indonesia sebesar 3,5%; tingkat pengembalian indeks pasar (E(rM)), dan risiko dari saham ke-i (βi). Hasil
perhitungan CAPM dapat disajikan pada Tabel 4 dan Tabel 5.
Tabel 4. Hasil Perhitungan Nilai Return Yang Diharapkan Pada Masing-masing Saham Menggunakan Beta CAPM-Stokastik
|
Saham |
rZ |
eom) |
Beta (βi) |
E(r;) = Tz + (E(T-M) - rf)βi |
|
HMSP |
0,035 |
-0,00022 |
1,90030 |
-0,03194 |
|
ICBP |
0,035 |
-0,00022 |
1,29882 |
-0,01075 |
|
KLBF |
0,035 |
-0,00022 |
1,44293 |
-0,01583 |
|
UNVR |
0,035 |
-0,00022 |
0,38044 |
0,02160 |
|
WOOD |
0,035 |
-0,00022 |
1,05731 |
-0,00224 |
Tabel 5. Hasil Perhitungan Nilai Return Yang Diharapkan Pada Masing-masing Saham Menggunakan Beta CAPM-Historis
|
Saham |
rZ |
E(Tm) |
Beta (βi) |
E(r;) = T + (E(Tm) - rf)βi |
|
HMSP |
0,035 |
-0,00047 |
1,18075 |
-0,00688 |
|
ICBP |
0,035 |
-0,00047 |
0,20786 |
0,02763 |
|
KLBF |
0,035 |
-0,00047 |
0,67198 |
0,01116 |
|
UNVR |
0,035 |
-0,00047 |
0,27375 |
0,02529 |
|
WOOD |
0,035 |
-0,00047 |
1,67418 |
-0,02439 |
Berdasarkan Tabel 4 dapat disimpulkan bahwa hasil perhitungan dengan CAPM-Stokastik pada saham UNVR nilai return yang diharapkan memiliki nilai terbesar yaitu 0,02160 dengan nilai risiko beta sebesar 0,38044. Sedangkan nilai return yang diharapkan paling kecil sebesar -0,03194 dengan nilai risiko beta sebesar 1,90030 dimiliki oleh saham HMSP. Pada Tabel 5 hasil perhitungan dengan CAPM-Historis pada saham ICBP memiliki nilai return yang diharapkan paling besar yaitu 0,02763 dengan nilai risiko beta sebesar 0,20786. Sedangkan nilai return yang diharapkan paling kecil yaitu -0,02439 dengan nilai risiko beta 1,67418 dimiliki oleh saham WOOD.
-
3.5 Penentuan Saham Efisien Berdasarkan
CAPM
Penentuan saham efisien dan tidak efisien berdasarkan perhitungan CAPM-Stokastik dan CAPM-Historis dapat disajikan pada Tabel 6.
Pada Tabel 6 hasil evaluasi dengan menggunakan CAPM-Stokastik diperoleh bahwa pada saham HMSP, ICBP, KLBF, dan WOOD termasuk ke dalam saham yang efisien sedangkan pada CAPM-Historis diperoleh
bahwa saham WOOD adalah saham yang efisien.
Tabel 6. Saham Efisien dan Tidak Efisien Berdasarkan CAPM
|
No. |
Saham |
CAPM-Stokastik | ||
|
ri |
e (r) |
Evaluasi | ||
|
1. |
HMSP |
-0,00297 |
-0,03194 |
Efisien |
|
2. |
ICBP |
-0,00007 |
-0,01075 |
Efisien |
|
3. |
KLBF |
-0,00057 |
-0,01583 |
Efisien |
|
4. |
UNVR |
-0,00091 |
0,02160 |
T idak Efisien |
|
5. |
WOOD |
0,00203 |
-0,00224 |
Efisien |
|
No. |
Saham |
CAPM-Historis | ||
|
ri |
Eft) |
Evaluasi | ||
|
1. |
HMSP |
-0,03181 |
-0,00688 |
Tidak Efisien |
|
2. |
ICBP |
0,00203 |
0,02763 |
Tidak Efisien |
|
3. |
KLBF |
-0,00369 |
0,01116 |
Tidak Efisien |
|
4. |
UNVR |
-0,01165 |
0,02529 |
Tidak Efisien |
|
5. |
WOOD |
0,02308 |
-0,02439 |
Efisien |
Dikatakan saham yang efisien karena nilai rata-rata return saham individu (ri) lebih besar daripada nilai return yang diharapkan (E(ri)). Hasil evaluasi CAPM-Stokastik pada saham UNVR termasuk saham yang tidak efisien sedangkan CAPM-Historis pada saham HMSP, ICBP, KLBF, dan UNVR termasuk saham yang tidak efisien. Disebut saham yang tidak efisien karena nilai rata-rata return saham individu (ri) lebih kecil daripada nilai return yang diharapkan (E(ri)). Sehingga perhitungan dengan menggunakan CAPM-Stokastik menghasilkan empat saham yang efisien dan satu saham yang tidak efisien sedangkan CAPM-Historis menghasilkan satu saham yang efisien yaitu saham WOOD, selain itu saham yang lain merupakan saham yang tidak efisien.
CAPM merupakan metode untuk menentukan saham efisien dan tidak efisien berdasarkan selisih antara nilai return individu dengan nilai return yang diharapkan berdasarkan CAPM. Dalam menentukan nilai return saham menggunakan CAPM dengan parameter stokastik langkah pertama adalah menentukan harga estimasi pada masing-masing saham menggunakan model GBG. Model ini dipengaruhi oleh beberapa parameter
yaitu harga saham awal, nilai rata-rata return saham (μ), dan nilai risiko saham (σ). Setelah memperoleh harga estimasi saham kemudian menghitung nilai return (ri) baru dari harga estimasi saham tersebut, kemudian menghitung nilai return pasar (rM\ selanjutnya menghitung nilai beta masing-masing saham (βi), dan menghitung nilai return yang diharapkan (E(ri) berdasarkan CAPM. Perhitungan CAPM-Stokastik diperoleh hasil evaluasi bahwa saham HMSP, ICBP, KLBF, dan WOOD termasuk ke dalam saham yang efisien sedangkan saham UNVR termasuk saham yang tidak efisien. Pada hasil evaluasi menggunakan CAPM-Historis menghasilkan bahwa pada saham HMSP, ICBP, KLBF, dan UNVR adalah saham yang tidak efisien sedangkan saham WOOD merupakan saham efisien.
Saran yang dapat diberikan peneliti untuk penelitian selanjutnya adalah memperluas objek penelitian mengenai perusahaan-perusahaan pada sektor lain sehingga dapat mengambil sampel lebih banyak dan periode penelitian yang berbeda sehingga memperoleh hasil yang lebih baik serta menerapkan model GBG dengan lompatan menggunakan beberapa parameter seperti parameter mu (μ), sigma (σ), dan gamma (γ) dalam mengestimasi harga saham
DAFTAR PUSTAKA
Abidin, S.N.Z. dan Jaffar, M.M. 2014. Forecasting Share Prices of Small Size Companies in Bursa Malaysia Using Geometric Brownian Motion. Applied Mathematics and Information Sciences. Vol. 8 No. 1, pp. 107-112. DOI: 10.12785/amis/080112
Ameliah, V., Dharmawan, K., dan Widana, I.N. 2017. Membandingkan Risiko Sistematis Menggunakan CAPM-GARCH dan CAPMEGARCH. E-Jurnal Matematika. Vol. 6 No. 4, pp. 241-247. DOI:
10.24843/MTK.2017.v06.i04. p172
Dmouj, A. 2006. Stock Price Modelling: Theory and Practice. Amsterdam: BMI Paper. DOI: 10.2139/ssrn.1109160
Haidiati, D., Topowijono., dan Azizah, D.F. 2016. Penerapan Metode Capital Asset Pricing Model (CAPM) Sebagai Dasar Pengambilan Keputusan Investasi Saham (Studi pada Perusahaan yang Terdaftar di
Indeks IDX30 Periode Juli 2012-Juni 2015). Jurnal Administrasi Bisnis. Vol. 37 No. 2.
Husnan, S. 2015. Dasar-Dasar Teori Portofolio dan Analisis Sekuritas. Yogyakarta: UPP STIM YKPN.
Liadi, E., Dharmawan, K., dan Nilakusmawati, D.P.E. 2020. Menentukan Saham Yang Efisien dengan Menggunakan Metode Capital Asset Pricing Model (CAPM). E-Jurnal Matematika. Vol. 9 No. 1, pp.23-30. DOI:10.24843/MTK.2020.v09.i01.p274
Tandelilin, E. 2017. Pasar Modal: Manajemen Portofolio & Investasi. Yogyakarta: Kanisius.
Yunita, R., Dharmawan, K., dan Harini, L.P.I. 2015. Menentukan Portofolio Optimal Pada Pasar Saham Yang Bergerak Dengan Model Gerak Brown Geometri Multidimensi. E-Jurnal Matematika. Vol. 4 No. 3, pp. 127134. DOI:
10.24843/MTK.2015.v04.i03.p100
257
Discussion and feedback