PENENTUAN PREMI DAN CADANGAN PADA ASURANSI PENDIDIKAN DENGAN MEMERHATIKAN PELUANG HIDUP ANAK

Written by NI LUH DE SISKA SARI DEWI, I NYOMAN WIDANA, KETUT JAYANEGARA
on November 30, 2021

E-Jurnal Matematika Vol. 10(4), November 2021, pp. 246-250

DOI: https://doi.org/10.24843/MTK.2021.v10.i04.p350

ISSN: 2303-1751

PENENTUAN PREMI DAN CADANGAN PADA ASURANSI PENDIDIKAN DENGAN MEMERHATIKAN PELUANG HIDUP ANAK

Ni Luh De Siska Sari Dewi^1§, I Nyoman Widana², Ketut Jayanegara³

¹Program Studi Matematika, Fakultas MIPA — Universitas Udayana [Email: [email protected]] ²Program Studi Matematika, Fakultas MIPA — Universitas Udayana [Email: [email protected]] ³Program Studi Matematika, Fakultas MIPA — Universitas Udayana [Email: [email protected]]

^§Corresponding Author

ABSTRACT

Education insurance provides services in the field of education. In education insurance, the insured not only gets protection benefits but also education funds. These benefits will be received if they have paid premiums. Insurance companies also need to set the exact amount of policy value. The purpose of this study is to determine the premium and policy value of education insurance by taking into account the child's life chances. In this study, used secondary data from the 2011 Indonesian Mortality Table and illustrated data in the form of education fund data. Premium is obtained using the equivalence principle and policy value is obtained using the prospective method. In the calculation of premiums and policy values for education insurance premiums by taking into account the child's life chances, modifications are made, the amount of education funds multiplied by the child's life chances. The results given in this study are the amount of education insurance premium by taking into account the child's life chances is Rp 6.946.456,00. Policy value increases during the disbursement of education funds and decreases at the end of coverage.

Keywords: Child’s life chances, Education insurance, Policy value, Premium.

1. PENDAHULUAN

Perencanaan masa depan merupakan upaya untuk meminimalkan risiko. Menurut Kamus Besar Bahasa Indonesia (KBBI), definisi dari risiko adalah akibat yang kurang menyenangkan (merugikan, membahayakan) dari suatu perbuatan atau tindakan. Salah satu produk yang dapat menjadi solusi dalam upaya perencanaan masa depan adalah asuransi. Asuransi adalah pemindahan risiko dari tertanggung kepada perusahaan asuransi (Rejda & McNamara, 2017). Pada asuransi, peserta asuransi atau yang disebut sebagai pihak tertanggung wajib membayar sejumlah uang yaitu premi kepada pihak penanggung (perusahaan asuransi).

Salah satu penunjang masa depan yang harus direncanakan dengan baik adalah pendidikan. Dalam menempuh pendidikan terdapat risiko yang mungkin terjadi. Mengingat pentingnya pendidikan dan risiko yang menyertainya maka perlu adanya suatu produk yang menjamin pendidikan seperti asuransi pendidikan yaitu asuransi jiwa yang memberikan pelayanan pada bidang pendidikan (Darmawi, 2006).

Perhitungan premi asuransi pendidikan dalam artikel ini dilakukan dengan memerhatikan peluang hidup anak. Hal ini berarti dana pendidikan hanya cair apabila anak masih hidup. Prinsip yang digunakan dalam perhitungan premi asuransi pendidikan dengan memerhatikan peluang hidup anak adalah prinsip ekuivalensi (jumlah uang yang masuk ke perusahaan sama dengan jumlah uang yang keluar dari perusahaan). Selain premi, dalam artikel ini juga ditentukan cadangan premi asuransi pendidikan. Menurut Sembiring (1986), cadangan premi adalah selisih nilai santunan dan nilai tunai pembayaran pada waktu pertanggungan. Metode yang digunakan untuk menentukan cadangan premi asuransi pendidikan dalam artikel ini adalah metode prospektif, yaitu metode yang didasarkan pada nilai sekarang dari total pendapatan di waktu yang akan datang (Futami, 1993). Tujuan dari penelitian ini yaitu menentukan premi dan cadangan pada asuransi pendidikan dengan memerhatikan peluang hidup anak.

Dalam artikel ini akan ditentukan nilai premi yang dibayarkan setiap tahun hingga akhir kontrak dengan syarat yang menjadi tertanggung masih hidup disebut sebagai premi tahunan bersih asuransi jiwa endowment. Perhitungan dilakukan dengan menggunakan simbol-simbol komutasi yaitu bentuk sederhana dari persamaan asuransi. Menurut Futami (1993), simbol-simbol komutasi yaitu sebagai berikut:

D_x — υ^χl_χ

n_x = d_x + d_x+1+d_x+2 + -

C_x = v^χ+1d_χ

^Mx — ^Cx ⁺^cx+i

⁺^cx+2

+ ∙∙∙

Besar premi tahunan bersih asuransi jiwa

endowment adalah:

A

P _ X:n\

^^χ-ⁿ∖ ^— a —

^X:n\

(1)

dengan anuitas berjangka awal tahun:

Nχ-Nχ+n

^X:n\ ∩

^dx

dan besarnya manfaat asuransi jiwa endowment adalah sebagai berikut:

Mχ-Mχ+n + Dχ+n

^Ax:n\ r∖

^u χ

Menurut Futami (1994), premi tahunan pada asuransi joint life dwiguna adalah:

A _ xy:ⁿ\

^χy.n∖ ^— p (2)

^χy.n∖

dengan anuitas berjangka awal tahun:

Nχy ^χ+n,y+n

∏ --------------

^χy.n∖ n

^u χy

dan besarnya manfaat asuransi jiwa endowment adalah:

_λ ^Mxy ^Mx+ny+n ^{+ D}x+ny+n

^Axyn\ ^— 5

^u χy

Simbol-simbol komutasi untuk asuransi

joint life adalah sebagai berikut:

y

Dχy=Vl^lχy

Nχy ^Dxy ^{+ D}x+1,y+1 ⁺ ∙

Cχy — V^⁺1dχy

^Mxy ^Cxy ^{+ C}x+1,y+1 ⁺ "'

Setelah dilakukan perhitungan premi, dapat ditentukan nilai dari cadangan premi. Cadangan premi yang didasarkan pada nilai sekarang dari total pengeluaran perusahaan di waktu yang akan datang dikurangi nilai sekarang dari total pendapatan perusahaan di waktu yang akan datang disebut metode prospektif. Besar

cadangan premi pada tahun ke-t berdasarkan metode prospektif adalah:

t^vχ∙-n∖ x_χ+t,∙.n-t∖ Xχ∙.rL∖Xχ+tnn-t∖ (3)

Cadangan premi untuk asuransi joint life dengan

metode prospektif:

U-A -r

t^v Xχ+ty+r-ι-t∖

xy:n\^x+ty+l:n-l\

(4)

2. METODE PENELITIAN

Dalam penelitian ini, data yang digunakan adalah data sekunder. Data tersebut berupa data peluang kematian yang bersumber dari Tabel Mortalitas Indonesia 2011. Selain itu, penelitian ini juga menggunakan data ilustrasi berupa dana pendidikan yang akan diperoleh tertanggung bersumber dari polis perusahaan asuransi. Langkah-langkah yang digunakan dalam penelitian ini adalah:

1. Menggunakan polis perusahaan asuransi terkait dana pendidikan pasti.
2. Menggunakan Tabel Mortalitas Indonesia 2011 untuk memperoleh tabel komutasi asuransi pendidikan.
3. Menghitung premi tahunan pada asuransi pendidikan tanpa memerhatikan peluang hidup anak (berdasarkan persamaan (1)).
4. Menentukan formula premi pada asuransi pendidikan dengan memerhatikan peluang hidup anak menggunakan prinsip ekuivalensi.
5. Menghitung nilai premi pada asuransi pendidikan dengan memerhatikan peluang hidup anak berdasarkan formula yang diperoleh.
6. Menghitung cadangan premi asuransi pendidikan dengan metode prospektif tanpa memerhatikan peluang hidup anak (berdasarkan persamaan (3)).
7. Menentukan formula cadangan premi asuransi pendidikan dengan memerhatikan peluang hidup anak menggunakan metode prospektif.
8. Menghitung cadangan premi asuransi pendidikan dengan memerhatikan peluang hidup anak berdasarkan formula yang diperoleh.

3. HASIL DAN PEMBAHASAN
- 3.1 Perhitungan Premi Tahunan Tanpa

Memerhatikan Peluang Hidup Anak

Polis yang digunakan pada perhitungan premi tahunan asuransi pendidikan tanpa memerhatikan peluang hidup anak dalam kasus ini adalah: pihak tertanggung dengan usia 39 tahun mengikuti asuransi pendidikan dalam jangka waktu 22 tahun. Dana pendidikan yang didapat tertanggung adalah 5% dari uang pertanggungan pada akhir tahun ke empat, 10% dari uang pertanggungan pada akhir tahun ke enam, 20% dari uang pertanggungan pada akhir tahun ke-12, 30% pada akhir tahun ke-15, 50% pada akhir tahun ke-18, 25% pada akhir tahun ke 19, 20, dan 21, serta 40% pada akhir tahun ke 22. Tertanggung yang meninggal dalam masa pertanggungan, akan menerima santunan sebesar 100% dari uang pertanggungan yaitu sebesar Rp 30.000.000,00. Masa pembayaran premi enam tahun, tingkat suku bunga 3,5%.

Berdasarkan polis yang ditetapkan, maka persamaan (1) dapat dimodifikasi menjadi:

-. -^p39:6|

3× 10⁷(Λ^2^) + ΛP(⁰) ^c⅝96∣

3× 10⁷(^^-M +/W'°

v D₃₉ /

= ‰-V45

O39

dengan XP⁽⁰⁾ adalah nilai tunai dari besar manfaat pendidikan tanpa memerhatikan hidup atau matinya anak dan besarnya adalah:

XP⁽⁰) = 3 × 10⁷(0,05v⁴ + 0,1v⁶ + 0,2v¹2

+ 0,3v¹≡ + 0,5v¹⁸ + 0,25v¹⁹

+ 0,25v²⁰+ 0,25v²¹

+ 0,4v²²)

Sehingga diperoleh besar premi asuransi pendidikan tanpa memerhatikan peluang hidup anak adalah:

2298057,8890+ 38107798,8800

^39:6| 5,4938

= 7354815,1850

3.2 Penentuan Premi Asuransi Pendidikan dengan Memerhatikan Peluang Hidup Anak

Polis yang digunakan pada perhitungan premi tahunan asuransi pendidikan dengan

memerhatikan peluang hidup anak sama seperti polis pada perhitungan premi tanpa memerhatikan peluang hidup anak, hanya saja dalam hal ini seorang ayah berusia 39 tahun mengikuti asuransi pendidikan pada saat anak berusia 0 tahun. Santunan diterima sebesar 100% dari uang pertanggungan apabila anak yang menjadi tertanggung meninggal dalam masa pertanggungan, dan dana pendidikan diterima apabila anak yang menjadi tertanggung masih hidup.

Dalam penentuan premi asuransi pendidikan dengan memerhatikan peluang hidup anak ditentukan terlebih dahulu peluang hidup anak mencapai usia tertentu. Menggunakan persamaan:

^lx+n

nPx =

^tχ

dengan l_χ adalah jumlah orang berusia % tahun dan l_χ+n adalah jumlah orang berusia % + n tahun.

Premi ditentukan berdasarkan prinspip ekuivalensi. Menurut Dickson et al. (2009), prinsip ekuivalensi dinyatakan sebagai:

E(r) = E(Z)

dengan Z adalah nilai tunai manfaat, dan Z adalah nilai tunai premi. Oleh karena itu, berdasarkan polis yang telah ditetapkan premi asuransi pendidikan dinyatakan sebagai:

_p _ S∙Λ⅛ + Λpω

^u xy:m|

dengan S adalah besarnya santunan yang akan diperoleh tertanggung, m adalah jangka waktu pembayaran premi, 4P⁽¹⁾ adalah nilai tunai dari besar manfaat pendidikan dengan memerhatikan hidup atau matinya anak yang menjadi tertanggung dan besarnya adalah:

^P⁽¹⁾ = 3 × 10⁷(0,05v⁴₄p₀ + 0,1v⁶₆p₀

+ 0,2v¹²12Po + 0,3v¹⁵1₅Po

+ 0,5v¹⁸18^0 + 0,25v¹⁹19^0

+ 0,25v²⅛0 + 0,25v²⅛0

+ 0,4v²⅛0

Sehingga diperoleh besar premi dengan memerhatikan peluang hidup anak sesuai polis yaitu:

3× 10⁷(Λ1 +

p _ __^0:22|_

^a0,39:6|

= 6946456,266

3.3 Perhitungan Cadangan Premi Tanpa Memerhatikan Peluang Hidup Anak

Berdasarkan polis yang ditetapkan, maka persamaan (3) dapat dimodifikasi menjadi:

.V —. = ς 4¹ ___-Pn --_r

t^K39:22| ^j'^zl39+t22-t∣ ^ru39+t:6-t|

+ ΛP_t(⁰)

dengan ΛP_t(⁰) merupakan nilai tunai dari besar manfaat pendidikan tanpa memerhatikan hidup atau matinya anak pada tahun ke-1.

untuk t=1,2,3,4

ΛP_t(⁰) = 3 × 10⁷(0,05v^4-t + 0,1v^6-t

+ 0,2v^12-t + 0,3v^15-t

+ 0,5v^18-t + 0,25v^19-t

+ 0,25v^20-t + 0,25v^21-t

+ 0,4v^22-t)

untuk t=5,6

ΛP_t(⁰) = 3 ×10⁷(0,1v^6-t+ 0,2v^12-t

+ 0,3v¹≡^-t + 0,5v^18-t

+ 0,25v^19-t+ 0,25v^20-t

+ 0,25v^21-t + 0,4v^22-t)

untuk t=7,8,9,10,11,12

ΛP_t(⁰) = 3 × 10⁷(0,2v^12-t + 0,3v¹≡^-t

+ 0,5v^18-t + 0,25v^19-t

+ 0,25v^20-t + 0,25v^21-t

+ 0,4v^22-t)

untuk t=13,14,15

ΛP_t(⁰) = 3 × 10⁷ (0,3v¹≡^-t + 0,5v^18-t

+ 0,25v^19-t+ 0,25v^20-t

+ 0,25v^21-t + 0,4v^22-t)

untuk t=16,17,18

ΛP_t(⁰) = 3 × 10⁷(0,5v^18-t + 0,25v^19-t

+ 0,25v^20-t + 0,25v^21-t

+ 0,4v^22-t)

untuk t=19

ΛP_t(⁰) = 3 × 10⁷(0,25v^19-t + 0,25v^20-t

+ 0,25v^21-t + 0,4v^22-t)

untuk t=20

ΛP_t(⁰) = 3 × 10⁷(0,25v^20-t + 0,25v^21-t

+ 0,4v^22-t)

untuk t=21

ΛP_t(⁰) = 3 × 10⁷(0,25v^21-t+ 0,4v^22-t)

untuk t=22

ΛP_t(⁰) = 3× 10⁷(0,4v^22-t)

Sehingga diperoleh besar cadangan premi seperti pada Gambar 1.

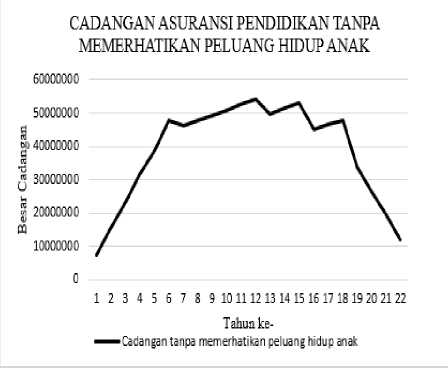
Gambar 1. Cadangan Tanpa Memerhatikan Peluang Hidup Anak

3.4 Perhitungan Cadangan Premi dengan Memerhatikan Peluang Hidup Anak

Berdasarkan polis yang ditetapkan, maka persamaan (4) dapat dimodifikasi menjadi:

¹

t^K0,39:22| ^a■^Λ0+t:22-t| ^{r u}0+t,39+r6→ |

+ ΛP_t^ω

untuk t=1,2,3,4

ΛP_t(¹) = 3 × 10⁷(0,05v^4-t_4-tp₀

+ O,lv^6-t6-_tP0

+ O,2v^12-t12-_tP0 + -

+ O,4v^22-t22-_tP0)

untuk t=5,6

ΛP_t(¹) = 3 × 10⁷(0,1v^6-t_6-tp₀

+ O,2v^12-t12-_tP0 + -

+ 0,4v^22-t22-_t⅛)

untuk t=7,8,9,10,11,12

ΛP_t^ω = 3 × 10⁷(0,2v^12-t_12-tp₀

+ ^0,3v¹≡^-t₁₅-_tP0

+ 0,5v^18-t18-_tp0 + -

+ 0,4v^22-t22-_tp0)

untuk t=13,14,15

ΛP_t(¹) = 3 × 10⁷(0,3v^15-t_15-tp₀

+ 0,5v^18-t18-_tP0

+ 0,25ι;^19-'_l9-∕⅛ + •••

+ O,4v^22-t22-_tP0)

untuk t=16,17,18

ΛP∞ = 3× 10⁷(0,5v^18-t_18-tp0

+ O,25v^19-ti9-_tpo

+ 0,25v²0^-t2o-_tPo

+ O,25v^21-t2i-_tpo

+ O,4v^22-t22-_tpo)

untuk t=19

ΛS_t^ω = 3 × 10⁷(0,25v^19-t_19-tp0

+ O,25v²0^-t2o-_tpo

+ O,25v^21-t21-_tpo

+ 0,4v^22-t22-_t⅛)

untuk t=20

ΛS_t^ω = 3 × 10⁷(0,25v^20-t₂0_-tp₀

+ O,25v^21-t21-_tpo

+ O,4v^22-t22-_tpo)

untuk t=21

ΛS_t^ω = 3 × 10⁷(0,25v^21-t_21-tp0 + 0,4V^22-t22-t⅛)

untuk t=22

ΛS_t^ω = 3 × 1O⁷(O,4v^22-t22-_tPo)

Sehingga diperoleh cadangan dengan memerhatikan peluang hidup anak pada tahun pertama yaitu sebagai berikut:

1^0,39:221 = S.Λ⅛ -P<⅛₅ +AP∞ = 6926183,0530

Diperoleh cadangan premi pada tahun pertama dengan memerhatikan peluang hidup anak yaitu Sp 6.926.183,00. Besar cadangan premi dengan memerhatikan peluang hidup anak dapat diperhatikan pada Gambar 2.

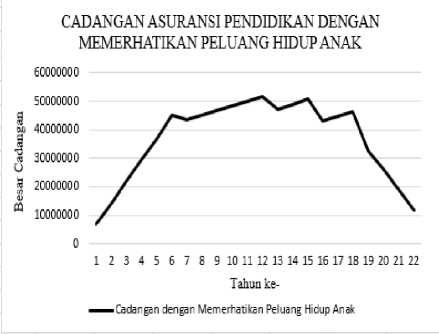
Gambar 2. Cadangan dengan Memerhatikan Peluang Hidup Anak

4. KESIMPULAN DAN SARAN

Kesimpulan yang diperoleh pada artikel ini adalah premi pada asuransi pendidikan dengan memerhatikan peluang hidup anak dapat ditentukan berdasarkan persamaan:

_{p =} 12⅛∏⁺^

^v⅛ym∣

Besar premi asuransi pendidikan berdasarkan formula yang diperoleh yaitu Sp 6.946.456,00. Cadangan premi asuransi pendidikan dengan memerhatikan peluang hidup anak dapat ditentukan dengan menggunakan persamaan:

.TZ 4 ¹ ___ -Pn ----_τ
t^l,x,yn∣ ^J./1x+t:n-t| ^{r u}x+t,y+t:m-1 |

+ ΛS_t^ω

Besar cadangan premi pada tahun pertama dengan memerhatikan peluang hidup anak yaitu Sp 6.926.183,00. Nilai cadangan premi menjadi lebih tinggi pada tahun-tahun pencairan dana pendidikan.

Pada penelitian ini tingkat suku bunga yang digunakan dalam perhitungan diasumsikan konstan. Pada kenyataannya tingkat suku bunga seringkali mengalami perubahan karena berbagai faktor. Disarankan dalam penelitian selanjutnya perhitungan dikembangkan dengan

menggunakan tingkat suku bunga tidak konstan.

DAFTAR PUSTAKA

Darmawi, H. 2006. Manajemen Asuransi.

Jakarta: Bumi Aksara.

Dickson, D. C. ., Hardy, M. R., & Waters, H. R.

2009. Actuarial Mathematics for Life Contingent Risks. New York: Cambridge University Press.

Futami, T. 1993. Matematika Asuransi Jiwa, Bagian I. 1st ed. Tokyo: Oriental Life Insurance Cultural Development Center.

Futami, T. 1994. Matematika Asuransi Jiwa, Bagian II. 2nd ed. Tokyo: Oriental Life Insurance Cultural Development Center.

Kamus Besar Bahasa Indonesia. [Online].

Tersedia di https://kbbi.web.id. Diakses 9 September 2020.

Rejda, G. E., & McNamara, M. . 2017.

Principles of Risk Management and Insurance. Harlow: Pearson.

Sembiring, R. K. 1986. Buku Materi Pokok Asuransi I. Jakarta: Universitas Terbuka.

250

PENENTUAN PREMI DAN CADANGAN PADA ASURANSI PENDIDIKAN DENGAN MEMERHATIKAN PELUANG HIDUP ANAK

PENENTUAN PREMI DAN CADANGAN PADA ASURANSI PENDIDIKAN DENGAN MEMERHATIKAN PELUANG HIDUP ANAK

nx = dx + dx+1+dx+2 + -

3× 107(Λ^2^) + ΛP(0) c⅝96∣

3× 107(^-M +/W'°

XP(0) = 3 × 107(0,05v4 + 0,1v6 + 0,2v12

+ 0,3v1≡ + 0,5v18 + 0,25v19

+ 0,25v20+ 0,25v21

+ 0,4v22)

2298057,8890+ 38107798,8800

39:6| 5,4938

= 7354815,1850

E(r) = E(Z)

p _ S∙Λ⅛ + Λpω

^P(1) = 3 × 107(0,05v44p0 + 0,1v66p0

+ 0,2v1212Po + 0,3v1515Po

+ 0,25v2⅛0 + 0,25v2⅛0

3× 107(Λ1 +

p _ ____________0:22|___________

= 6946456,266

+ ΛPt(0)

ΛPt(0) = 3 × 107(0,05v4-t + 0,1v6-t

+ 0,2v12-t + 0,3v15-t

+ 0,5v18-t + 0,25v19-t

+ 0,25v20-t + 0,25v21-t

+ 0,4v22-t)

ΛPt(0) = 3 ×107(0,1v6-t+ 0,2v12-t

+ 0,3v1≡-t + 0,5v18-t

+ 0,25v19-t+ 0,25v20-t

+ 0,25v21-t + 0,4v22-t)

ΛPt(0) = 3 × 107(0,2v12-t + 0,3v1≡-t

+ 0,5v18-t + 0,25v19-t

+ 0,25v20-t + 0,25v21-t

+ 0,4v22-t)

ΛPt(0) = 3 × 107 (0,3v1≡-t + 0,5v18-t

+ 0,25v19-t+ 0,25v20-t

+ 0,25v21-t + 0,4v22-t)

ΛPt(0) = 3 × 107(0,5v18-t + 0,25v19-t

+ 0,25v20-t + 0,25v21-t

+ 0,4v22-t)

ΛPt(0) = 3 × 107(0,25v19-t + 0,25v20-t

+ 0,25v21-t + 0,4v22-t)

ΛPt(0) = 3 × 107(0,25v20-t + 0,25v21-t

+ 0,4v22-t)

ΛPt(0) = 3 × 107(0,25v21-t+ 0,4v22-t)

ΛPt(0) = 3× 107(0,4v22-t)

1

+ ΛPtω

ΛPt(1) = 3 × 107(0,05v4-t4-tp0

+ O,lv6-t6-tP0

+ O,2v12-t12-tP0 + -

+ O,4v22-t22-tP0)

ΛPt(1) = 3 × 107(0,1v6-t6-tp0

+ O,2v12-t12-tP0 + -

+ 0,4v22-t22-t⅛)

ΛPtω = 3 × 107(0,2v12-t12-tp0

+ 0,3v1≡-t15-tP0

+ 0,5v18-t18-tp0 + -

+ 0,4v22-t22-tp0)

ΛPt(1) = 3 × 107(0,3v15-t15-tp0

+ 0,5v18-t18-tP0

+ 0,25ι;19-'l9-∕⅛ + •••

+ O,4v22-t22-tP0)

ΛP∞ = 3× 107(0,5v18-t18-tp0

+ O,25v19-ti9-tpo

+ 0,25v20-t2o-tPo

+ O,25v21-t2i-tpo

+ O,4v22-t22-tpo)

ΛStω = 3 × 107(0,25v19-t19-tp0

+ O,25v20-t2o-tpo

+ O,25v21-t21-tpo

+ 0,4v22-t22-t⅛)

ΛStω = 3 × 107(0,25v20-t20-tp0

+ O,25v21-t21-tpo

+ O,4v22-t22-tpo)

ΛStω = 3 × 107(0,25v21-t21-tp0 + 0,4V22-t22-t⅛)

ΛStω = 3 × 1O7(O,4v22-t22-tPo)

1^0,39:221 = S.Λ⅛ -P<⅛5 +AP∞ = 6926183,0530

+ ΛStω

Discussion and feedback

n_x = d_x + d_x+1+d_x+2 + -

3× 10⁷(Λ^2^) + ΛP(⁰) ^c⅝96∣

3× 10⁷(^^-M +/W'°

XP⁽⁰) = 3 × 10⁷(0,05v⁴ + 0,1v⁶ + 0,2v¹2

+ 0,3v¹≡ + 0,5v¹⁸ + 0,25v¹⁹

+ 0,25v²⁰+ 0,25v²¹

+ 0,4v²²)

^39:6| 5,4938

_p _ S∙Λ⅛ + Λpω

^P⁽¹⁾ = 3 × 10⁷(0,05v⁴₄p₀ + 0,1v⁶₆p₀

+ 0,2v¹²12Po + 0,3v¹⁵1₅Po

+ 0,25v²⅛0 + 0,25v²⅛0

3× 10⁷(Λ1 +

p _ __^0:22|_

+ ΛP_t(⁰)

ΛP_t(⁰) = 3 × 10⁷(0,05v^4-t + 0,1v^6-t

+ 0,2v^12-t + 0,3v^15-t

+ 0,5v^18-t + 0,25v^19-t

+ 0,25v^20-t + 0,25v^21-t

+ 0,4v^22-t)

ΛP_t(⁰) = 3 ×10⁷(0,1v^6-t+ 0,2v^12-t

+ 0,3v¹≡^-t + 0,5v^18-t

+ 0,25v^19-t+ 0,25v^20-t

+ 0,25v^21-t + 0,4v^22-t)

ΛP_t(⁰) = 3 × 10⁷(0,2v^12-t + 0,3v¹≡^-t

+ 0,5v^18-t + 0,25v^19-t

+ 0,25v^20-t + 0,25v^21-t

+ 0,4v^22-t)

ΛP_t(⁰) = 3 × 10⁷ (0,3v¹≡^-t + 0,5v^18-t

+ 0,25v^19-t+ 0,25v^20-t

+ 0,25v^21-t + 0,4v^22-t)

ΛP_t(⁰) = 3 × 10⁷(0,5v^18-t + 0,25v^19-t

+ 0,25v^20-t + 0,25v^21-t

+ 0,4v^22-t)

ΛP_t(⁰) = 3 × 10⁷(0,25v^19-t + 0,25v^20-t

+ 0,25v^21-t + 0,4v^22-t)

ΛP_t(⁰) = 3 × 10⁷(0,25v^20-t + 0,25v^21-t

+ 0,4v^22-t)

ΛP_t(⁰) = 3 × 10⁷(0,25v^21-t+ 0,4v^22-t)

ΛP_t(⁰) = 3× 10⁷(0,4v^22-t)

¹

+ ΛP_t^ω

ΛP_t(¹) = 3 × 10⁷(0,05v^4-t_4-tp₀

+ O,lv^6-t6-_tP0

+ O,2v^12-t12-_tP0 + -

+ O,4v^22-t22-_tP0)

ΛP_t(¹) = 3 × 10⁷(0,1v^6-t_6-tp₀

+ O,2v^12-t12-_tP0 + -

+ 0,4v^22-t22-_t⅛)

ΛP_t^ω = 3 × 10⁷(0,2v^12-t_12-tp₀

+ ^0,3v¹≡^-t₁₅-_tP0

+ 0,5v^18-t18-_tp0 + -

+ 0,4v^22-t22-_tp0)

ΛP_t(¹) = 3 × 10⁷(0,3v^15-t_15-tp₀

+ 0,5v^18-t18-_tP0

+ 0,25ι;^19-'_l9-∕⅛ + •••

+ O,4v^22-t22-_tP0)

ΛP∞ = 3× 10⁷(0,5v^18-t_18-tp0

+ O,25v^19-ti9-_tpo

+ 0,25v²0^-t2o-_tPo

+ O,25v^21-t2i-_tpo

+ O,4v^22-t22-_tpo)

ΛS_t^ω = 3 × 10⁷(0,25v^19-t_19-tp0

+ O,25v²0^-t2o-_tpo

+ O,25v^21-t21-_tpo

+ 0,4v^22-t22-_t⅛)

ΛS_t^ω = 3 × 10⁷(0,25v^20-t₂0_-tp₀

+ O,25v^21-t21-_tpo

+ O,4v^22-t22-_tpo)

ΛS_t^ω = 3 × 10⁷(0,25v^21-t_21-tp0 + 0,4V^22-t22-t⅛)

ΛS_t^ω = 3 × 1O⁷(O,4v^22-t22-_tPo)

1^0,39:221 = S.Λ⅛ -P<⅛₅ +AP∞ = 6926183,0530

+ ΛS_t^ω