SMOTE: POTENSI DAN KEKURANGANNYA PADA SURVEI
on
E-Jurnal Matematika Vol. 10(4), November 2021, pp. 235-240
DOI: https://doi.org/10.24843/MTK.2021.v10.i04.p348
ISSN: 2303-1751
SMOTE: POTENSI DAN KEKURANGANNYA PADA SURVEI
Ni Putu Yulika Trisna Wijayanti1§, Eka N Kencana2, I Wayan Sumarjaya3
1Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: yulika.wijayanti@gmail.com] 2Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: i.putu.enk@unud.ac.id] 3Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: sumarjaya@unud.ac.id] §Corresponding Author
ABSTRACT
Imbalanced data is a problem that is often found in real-world cases of classification. Imbalanced data causes misclassification will tend to occur in the minority class. This can lead to errors in decision-making if the minority class has important information and it’s the focus of attention in research. Generally, there are two approaches that can be taken to deal with the problem of imbalanced data, the data level approach and the algorithm level approach. The data level approach has proven to be very effective in dealing with imbalanced data and more flexible. The oversampling method is one of the data level approaches that generally gives better results than the undersampling method. SMOTE is the most popular oversampling method used in more applications. In this study, we will discuss in more detail the SMOTE method, potential, and disadvantages of this method. In general, this method is intended to avoid overfitting and improve classification performance in the minority class. However, this method also causes overgeneralization which tends to be overlapping.
Keywords: Imbalanced Data, Oversampling, SMOTE
Data tidak seimbang merupakan permasalahan yang sering ditemukan pada kasus nyata dalam klasifikasi. Data tidak seimbang terjadi ketika jumlah pengamatan pada data latih untuk setiap label kelas tidak seimbang, di mana kondisi jumlah data pada suatu kelas jauh lebih banyak dibandingkan kelas lainnya. Kelas dengan jumlah data yang lebih banyak disebut kelas mayoritas sedangkan kelas dengan jumlah data yang lebih sedikit disebut dengan kelas minoritas (Brownlee, 2020).
Data tidak seimbang menyebabkan kesalahan klasifikasi akan cenderung terjadi pada kelas minoritas. Kelas minoritas akan lebih sulit untuk diprediksi karena hanya ada sedikit data pada kelas tersebut jika dibandingkan dengan kelas mayoritas. Banyak makalah penelitian tentang data tidak seimbang sepakat bahwa distribusi kelas yang tidak merata menyebabkan pengklasifikasi bias terhadap kelas mayoritas. Hal ini dikarenakan secara umum algoritma klasifikasi standar pada pembelajaran mesin cenderung mengasumsikan distribusi kelas yang sama. Sehingga, pada kasus data tidak seimbang model klasifikasi
akan cenderung berfokus untuk mempelajari karakteristik data pada kelas mayoritas dan mengabaikan kelas minoritas (Singh dan Sharma, 2019).
Hal tersebut dapat menyebabkan kesalahan dalam pengambilan keputusan, apabila kelas minoritas memiliki informasi penting dan menjadi fokus perhatian dalam penelitian. Sebagai contoh pada kasus deteksi penyakit kanker, deteksi spam, deteksi penipuan, churn prediction dan lain-lain.
Umumnya terdapat dua pendekatan yang dapat dilakukan untuk menangani permasalahan data tidak seimbang, yakni pendekatan level data dan pendekatan level algoritma. Pendekatan pada level data dilakukan dengan menyeimbangkan distribusi kelas mayoritas dan minoritas dengan teknik pengambilan sampel seperti undersampling, oversampling, maupun kombinasi dari kedua metode tersebut. Sedangkan pendekatan pada level algoritma dilakukan dengan memodifikasi dan mengoptimalkan kinerja algoritma pembelajaran mesin (Santoso et al., 2017).
Menurut He dan Garcia dalam Maldonado, et al. (2019) pengambilan sampel pada data telah terbukti sangat efektif untuk menangani data tidak seimbang. Pengambilan sampel merupakan pendekatan pada level data. Keuntungan dari pendekatan level data ini yakni tidak bergantung pada pengklasifikasi yang digunakan dan pendekatan ini dinilai lebih fleksibel (Ramyachitra dan Manikandan, 2014).
Undersampling dilakukan dengan mengurangi atau mengeliminasi beberapa data pada kelas mayoritas untuk menyeimbangkan distribusi kelas, sedangkan oversampling dilakukan dengan menambahkan data pada kelas minoritas. Pada umumnya metode oversampling lebih sering digunakan dibandingkan undersampling. Hal ini dikarenakan metode undersampling mengurangi data pada kelas mayoritas sehingga dapat menghilangkan informasi penting pada data tersebut. Menurut Batista, et al. dalam Santoso, et al. (2017) metode oversampling umumnya memberikan hasil yang lebih baik dibandingkan metode undersampling.
Metode oversampling paling dasar dilakukan dengan menduplikasi data secara acak pada kelas minoritas, yang disebut dengan random oversampling. Namun, metode ini cenderung mengakibatkan overfitting, karena dilakukan penduplikasian data yang telah ada sebelumnya sehingga pengklasifikasi terkena informasi yang sama. Untuk mengatasi permasalahan tersebut Chawla, et al. (2002) mengusulkan metode synthetic minority oversampling technique (SMOTE).
SMOTE merupakan metode oversampling yang paling populer digunakan. SMOTE dilakukan dengan menambah data sintetis pada kelas minoritas. Data sintetis merupakan data baru yang dibangkitkan. Walaupun populer, metode SMOTE tetap memiliki kekurangan yang mendorong pengembangan penelitian untuk mengatasi permasalahan tersebut. Sehingga, pada kajian ini akan dibahas lebih mendalam mengenai potensi dan kekurangan dari metode SMOTE.
Ha dan Bunke dalam Chawla, et al. (2002) menyarankan pengambilan sampel berlebih pada kelas minor dilakukan dengan membuat sampel sintetis yakni sampel baru yang dibangkitkan dibanding melakukan duplikasi data. SMOTE dilakukan dengan menambah
jumlah data pada kelas minoritas dengan cara membangkitkan data baru berdasarkan k tetangga terdekat. Data pada kelas minoritas dilakukan oversampling dengan mengambil data pada kelas minoritas dan menambah sampel sintetis di sepanjang garis yang menghubungkan salah satu atau semua k tetangga terdekat data kelas minoritas tersebut. Jumlah tetangga k dipilih secara acak.
Formula untuk membangkitkan data sintetis dengan SMOTE adalah sebagai berikut:
Knew = Xi + (Xk - Xi) × S
di mana Xnew = data sintetis baru, Xi = data dari kelas minoritas, Xk = data dari k tetangga terdekat yang memiliki jarak terdekat dengan Xi, dan S = bilangan acak antara 0 dan 1. Perbedaan jarak dalam menentukan tetangga terdekat pada data numerik dilakukan dengan menggunakan jarak Euclid.
Pada makalah algoritma SMOTE asli, beberapa modifikasi telah diusulkan dalam literatur. Pendekatan SMOTE tidak menangani kumpulan data dengan semua fitur yang berskala nominal dan hal tersebut dikembangkan untuk menangani kumpulan data dengan fitur berskala campuran yakni nominal dan kontinu. Chawla, et al. (2002) mengusulkan synthetic minority oversampling technique nominal (SMOTE-N) untuk kumpulan data dengan semua fitur berskala nominal, dan synthetic minority oversampling technique nominal continuous (SMOTE-NC) untuk kumpulan data berskala nominal dan kontinu.
Perhitungan tetangga terdekat kelas minoritas fitur nominal pada SMOTE-N dilakukan dengan menggunakan value difference metric (VDM) dengan formula:
N
∆(X,Y} =wxwy∑δ(Xi,yiy i=i
di mana wxwy = bobot amatan, N = banyaknya fitur penjelas, r = bernilai 1 (jarak Manhattan) atau 2 (jarak Euclid), dan S(xi,yi) = jarak antar fitur nominal dengan formula:
n
-
*x^ = ∑⅛-% U-I Uol
i=i 1 2
di mana C1 = banyaknya xi terjadi, C1i = banyaknya xi yang termasuk kelas i, C2 = banyaknya yi terjadi, C2i = banyaknya yi yang
termasuk kelas i, n = banyaknya kelas, dan k = konstanta (biasanya 1).
SMOTE-NC dilakukan dengan menghitung median deviasi standar semua fitur/variabel kontinu untuk kelas minoritas. Perhitungan jarak Euclid dilakukan dengan menggunakan fitur kontinu dan menyertakan median deviasi standar yang telah dihitung sebelumnya. Pembangkitan data sintetis untuk fitur kontinu dilakukan sama dengan metode SMOTE sedangkan untuk fitur nominal dilakukan dengan memilih nilai mayoritas dari k tetangga terdekat (Chawla et al., 2002).
Pada dasarnya SMOTE adalah salah satu penerapan dari metode oversampling. Sehingga salah satu kelebihan metode ini adalah tidak akan menyebabkan adanya informasi yang hilang, dikarenakan tidak ada pengurangan data seperti yang dilakukan pada metode undersampling.
Jika dibandingkan dengan oversampling yang dilakukan dengan duplikasi (random oversampling) kelebihan SMOTE dapat dilihat dengan mempertimbangkan efek pada wilayah keputusan dalam ruang fitur. Dengan duplikasi, wilayah keputusan untuk kelas minoritas dapat menjadi lebih kecil dan spesifik, hal ini dikarenakan sampel minoritas di wilayah tersebut diduplikasi yang menyebabkan adanya kecenderungan untuk overfitting. Sedangkan, dengan pembangkitan data sintetis (SMOTE) dapat menyebabkan pengklasifikasi membangun wilayah keputusan yang lebih besar dan kurang spesifik pada kelas minoritas.
SMOTE menyediakan sampel pada kelas minoritas yang lebih terkait untuk dipelajari oleh pengklasifikasi, sehingga pengklasifikasi memiliki cakupan yang lebih besar dalam mempelajari kelas minoritas. Hal tersebut menyebabkan pendekatan SMOTE mampu meningkatkan nilai akurasi pengklasifikasi pada kelas minoritas, jika dibandingkan oversampling dengan duplikasi (Chawla et al. 2002).
Meskipun SMOTE cukup efektif dalam meningkatkan akurasi klasifikasi pada kelas minoritas, namun masih terdapat permasalahan pada metode ini. Salah satu permasalahan utama pada SMOTE adalah terjadinya overgeneralization (generalisasi yang berlebih). Data sintetis hasil SMOTE dapat memungkinkan tersebar pada wilayah kelas minoritas maupun mayoritas, di mana hal ini
dapat menyebabkan menurunnya kinerja pengklasifikasi (Santoso et al., 2017).
Sejak kelas mayoritas diabaikan oleh metode ini, data sintetis yang dihasilkan dapat dibuat di atas kelas mayoritas, hal ini menyebabkan terjadinya overlapping (tumpang tindih). Ilustrasi overlapping dapat dilihat pada Gambar 1. Data sintetis baru (dilambangkan dengan kotak berwarna kuning) terletak di wilayah yang didominasi oleh data pada kelas mayoritas mengindikasikan kondisi overlapping dan mengaburkan batas antar kelas.
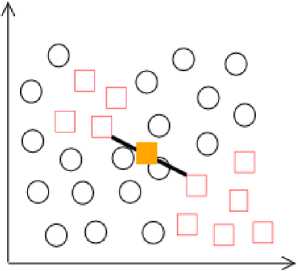
Gambar 1. Ilustrasi permasalahan overgeneralization pada SMOTE
Berdasarkan formula untuk membangkitkan data sintetis dengan SMOTE, jarak antara data minoritas dan tetangga terdekatnya dikalikan dengan bilangan acak antara 0 dan 1. Jika bilangan acak mendekati 0 maka data sintetis akan serupa dengan data minoritas asal. Sebaliknya, jika bilangan acak mendekati 1 maka data sintetis akan serupa dengan tetangga terdekat. Masalah yang dapat terjadi adalah jika bilangan acak sekitar 0,5 memungkinkan data sintetis yang dihasilkan akan serupa dengan data mayoritas. Inilah penyebab generalisasi yang berlebihan (Santoso et al., 2017).
Tetangga terdekat pada metode SMOTE dicari dengan menghitung perbedaan jarak, yang biasanya dihitung menggunakan jarak Euclid. Namun, permasalahan muncul di mana sejumlah kecil fitur memiliki kepentingan atau nilai korelasi yang tinggi dengan fitur lainnya. Mencari tetangga terdekat dengan jarak Euclid tanpa mempertimbangkan kepentingan tersebut akan menghasilkan tetangga yang tidak representatif (Fahrudin et al., 2019).
Penggunaan jarak Euclid juga menimbulkan permasalahan pada kasus kumpulan data berdimensi tinggi. Jarak Euclid tidak sesuai digunakan pada kasus data berdimensi tinggi karena konsep kedekatan tidak terdefinisi
dengan baik. Jarak Euclid mengasumsikan bahwa semua fitur memiliki kepentingan yang sama, sedangkan data berdimensi tinggi biasanya memiliki fitur yang tidak relevan yakni fitur yang tidak merepresentasikan permasalahan dalam pemodelan, di mana hal ini akan menimbulkan noise pada algoritma (Maldonado, 2019).
Chawla, et al. (2002) pada makalahnya menyarankan untuk mempertimbangkan lebih lanjut beberapa topik untuk meningkatkan kinerja metode SMOTE, secara khusus yakni mengenai strategi untuk menentukan tetangga terdekat. Permasalahan yang muncul pada metode SMOTE, mendorong berbagai penelitian lanjutan modifikasi SMOTE untuk menciptakan teknik yang lebih efektif dalam meningkatkan kinerja klasifikasi.
Beberapa perkembangan dari metode SMOTE diantaranya, Chawla, et al. (2003) mengusulkan SMOTEBoost. Metode tersebut merupakan kombinasi dari metode SMOTE dan prosedur boosting standar dengan tujuan untuk meningkatkan akurasi prediksi kelas minoritas tanpa mengorbankan akurasi pada keseluruhan data.
Data tidak seimbang sering menyebabkan klaster kelas tidak didefinisikan dengan baik karena beberapa data kelas mayoritas mungkin berada pada kelas minoritas sehingga menyebabkan noise. Batista, et al. (2004) memperbaiki kinerja metode SMOTE dengan menghapus data tersebut dengan tomek links (SMOTE-Tomeks Link), selain itu perbaikan juga dilakukan pada kedua kelas minoritas dan mayoritas dengan edited nearest neighbor (SMOTE-ENN). Motivasi utama kedua metode tersebut tidak hanya menyeimbangkan data latih, tetapi juga menghilangkan data noise yang memungkinkan pembuatan model yang lebih sederhana dan kemampuan generalisasi yang lebih baik.
Han, et al. (2005) mengembangkan metode SMOTE yang berfokus pada daerah perbatasan (borderline) antara batas data kelas minoritas dan mayoritas. Motivasi metode tersebut, karena sebagian besar algoritma klasifikasi berusaha mempelajari garis batas setiap kelas setepat mungkin pada proses pelatihan. Data yang berada pada garis batas atau di dekatnya akan cenderung salah diklasifikasikan dibandingkan data yang terletak jauh dari garis batas. Sehingga, pembangkitan data sintetis hanya dilakukan pada daerah perbatasan (SMOTE-Borderline). Pada metode ini, bilangan acak
yang digunakan untuk membangkitkan data yakni antara 0 sampai 0,5 dengan harapan data sintetis yang dihasilkan akan serupa dengan data minoritas dan menghindari terjadinya overlapping.
He, et al. (2008) mengusulkan metode adaptuve synthetic sampling approach (ADASYN). Metode tersebut menggunakan distribusi berbobot pada kelas minoritas sesuai dengan tingkat kesulitan pembelajaran. Data sintetis akan dihasilkan lebih banyak pada kelas minoritas yang sulit untuk dipelajari dibandingkan kelas minoritas yang mudah dipelajari.
Bunkhumpornpat, et al. (2009) lebih berfokus memperhatikan daerah aman (safe), merupakan data yang ditempatkan didaerah yang relatif homogen dengan kelas minoritas. Metode tersebut disebut Safe Level SMOTE, di mana data sintetis dihasilkan lebih banyak pada daerah aman, sehingga menghasilkan kinerja akurasi yang lebih baik.
Selanjutnya Ramentol, et al. (2011) menggunakan teori Rough Set untuk meningkatkan data sintetis yang dihasilkan oleh metode SMOTE, metode ini disebut SMOTE-RSB. Douzas dan Bacao (2017) mengusulkan metode geometric SMOTE (G-SMOTE) dengan membangkitkan data sintetis di ruang input geometris yakni truncated hyper-spheroid, di sekitar data minoritas yang terpilih.
Untuk mengatasi permasalahan pada kumpulan data dengan dimensi tinggi, Maldonado, et al. (2019) mengusulkan metode SMOTE-Subset of Features (SMOTE-SF). Metode tersebut menambahkan pemeringkatan fitur sebelum didefinisikan sebagai tetangga, perhitungan jarak hanya menggunakan beberapa fitur. Menggunakan metrik baru berdasarkan jarak Minkowski seperti jarak Chebyshev dan Manhattan.
Perkembangan lain dari metode ini diusulkan oleh Fahrudin, et al. (2019) yakni AWH-SMOTE (attribute weighted and kNN Hub). Peningkatan kinerja dilakukan dengan mengidentifikasi noise menggunakan attribute weighted dan pengambilan sampel selektif dengan menghitung kemunculan data di semua kelas minoritas kNN (kNN hub). Data minoritas dengan kemunculan jumlah data yang kecil memiliki nilai aman (safe value) yang rendah. Hal tersebut menunjukkan bahwa data minoritas tersebut jauh dari titik pusat kelas minoritas dan daerah tersebut memiliki banyak data mayoritas, sehingga data sintetis akan dibangun pada
daerah tersebut.
Selanjutnya, Guan, et al. (2020)
mengusulkan metode SMOTE-WENN yakni menggabungkan metode SMOTE dengan pendekatan pembersihan data weighted edited nearest neighbor (WENN). WENN menghapus data kelas minoritas dan mayoritas yang tidak aman menggunakan weighted distance function dan kNN. Weighted distance function mempertimbangkan ketakseimbangan lokal dan spacial sparsity. Perkembangan dan modifikasi dari metode SMOTE masih terus dilakukan dalam penelitian untuk meningkatkan kinerja klasifikasi pada kasus data tidak seimbang.
Kelebihan dari metode SMOTE secara umum adalah tidak menyebabkan adanya informasi yang hilang, menghindari terjadinya overfitting, membangun wilayah keputusan yang lebih besar, serta mampu meningkatkan akurasi prediksi kelas minoritas. Kekurangan dari metode ini adalah, overgeneralization yang menyebabkan terjadinya overlapping, tidak tepat digunakan pada kasus yang mempertimbangkan kepentingan fitur dan kumpulan data dengan dimensi tinggi. Untuk mengatasi permasalahan tersebut, beberapa perkembangan dan modifikasi dilakukan pada metode ini. Walaupun demikian, SMOTE tetap merupakan pelopor perkembangan teknik oversampling yang menggunakan data sintetis.
DAFTAR PUSTAKA
Batista, G.E., Prati, R.C. and Monard, M.C., 2004. A Study of the Behavior of Several Methods for Balancing Machine Learning Training Data. ACM SIGKDD explorations newsletter, 6(1), pp.20-29.
Brownlee, J., 2020. Data Preparation for
Machine Learning. San Francisco: Machine Learning Mastery.
Bunkhumpornpat, C., Sinapiromsaran, K. and Lursinsap, C., 2009. Safe-Level-SMOTE: Safe-Level-Synthetic Minority OverSampling Technique for Handling the Class Imbalanced Problem. Pacific-Asia
conference on knowledge discovery and data mining, pp.475-482. Springer, Berlin,
Heidelberg.
Chawla, N.V., Bowyer, K.W., Hall, L.O. and Kegelmeyer, W.P., 2002. SMOTE: Synthetic
Minority Over-Sampling Technique. Journal of artificial intelligence research, 16,
pp.321-357.
Chawla, N.V., Lazarevic, A., Hall, L.O. and Bowyer, K.W., 2003. SMOTEBoost:
Improving Prediction of the Minority Class in Boosting. European conference on principles of data mining and knowledge discovery, pp.107-119. Springer, Berlin,
Heidelberg.
Douzas, G. and Bacao, F., 2017. Geometric SMOTE: Effective Oversampling for
Imbalanced Learning Through A Geometric Extension of SMOTE. arXiv preprint arXiv:1709.07377.
Fahrudin, T., Buliali, J.L. and Fatichah, C., 2019. Enhancing the Performance of SMOTE Algorithm by Using Attribute Weighting Scheme and New Selective Sampling Method for Imbalanced Data set. Int J Innov Comput Inf Control, 15, pp.423-444.
Guan, H., Zhang, Y., Xian, M., Cheng, H.D. and Tang, X., 2021. SMOTE-WENN: Solving Class Imbalance and Small Sample Problems by Oversampling and Distance Scaling. Applied
Intelligence, 51(3), pp.1394-1409.
Han, H., Wang, W.Y. and Mao, B.H., 2005. Borderline-SMOTE: A New Over-Sampling Method in Imbalanced Data Sets Learning. International conference on intelligent computing, pp.878-887. Springer, Berlin, Heidelberg.
He, H., Bai, Y., Garcia, E.A. and Li, S., 2008. ADASYN: Adaptive Synthetic Sampling Approach for Imbalanced Learning. IEEE international joint conference on neural networks (IEEE world congress on computational intelligence), pp.1322-1328.
Maldonado, S., López, J. and Vairetti, C., 2019. An Alternative SMOTE Oversampling Strategy for High-Dimensional
Datasets. Applied Soft Computing, 76,
pp.380-389.
Ramentol, E., Caballero, Y., Bello, R. and Herrera, F., 2012. SMOTE-RSB*: A Hybrid Preprocessing Approach Based on Oversampling and Undersampling for High Imbalanced Data-Sets Using SMOTE and
Rough Sets Theory. Knowledge and information systems, 33(2), pp.245-265.
Ramyachitra, D. and Manikandan, P., 2014. Imbalanced Dataset Classification and
Solutions: A Review. International Journal of Computing and Business Research (IJCBR), 5(4), pp.1-29.
Santoso, B., Wijayanto, H., Notodiputro, K.A. and Sartono, B., 2017. Synthetic Over
Sampling Methods for Handling Class Imbalanced Problems: A review. IOP conference series: earth and environmental science, 58(1). IOP Publishing.
Singh, P. dan Sharma, P. A. 2019. Analysis of Imbalanced Classification Algorithms: A Perspective View. International Journal of Trend in Scientific Research and Development, 3(2), pp.974-978.
240
Discussion and feedback