PERAMALAN VOLATILITAS DAN ESTIMASI VALUE AT RISK (VaR) SAHAM BLUE CHIP PADA SEKTOR PERBANKAN
on
E-Jurnal Matematika Vol. 10(4), November 2021, pp. 198-208
DOI: https://doi.org/10.24843/MTK.2021.v10.i04.p343
ISSN: 2303-1751
PERAMALAN VOLATILITAS DAN ESTIMASI VALUE AT RISK (VaR) SAHAM BLUE CHIP PADA SEKTOR PERBANKAN
Ni Kadek Juliarini1§, I Wayan Sumarjaya2, Kartika Sari3
1Program Studi Matematika, Fakultas MIPA-Universitas Udayana [Email:juliarini90799@yahoo.com] 2Program Studi Matematika, Fakultas MIPA-Universitas Udayana [Email:sumarjaya@unud.ac.id] 3Program Studi Matematika, Fakultas MIPA-Universitas Udayana [Email:sarikartika@unud.ac.id] §Corresponding Author
ABSTRACT
Investment is an activity to invest an asset to obtain a greater profit. The investment there's in great demand by investors are stock investments. Based on market capitalization, stocks are classified into first-tier, second-tier, and third-tier stocks. Stocks that have the highest market capitalization are first-tier or blue-chip stocks. Blue-chip stocks are stocks that are classified as main shares on the listing board on the IDX. Before investing, it's important to know the level of investment risk in order to make the right investment decisions. The purpose of this study is to determine the risk of investing in blue-chip stocks namely BRI, BCA, and Bank Mandiri through volatility forecasting using the GARCH, EGARCH, or TGARCH models. The data used is the daily closing price of shares for the period of 25 May 2005 to 21 May 2021 which was obtained through the Yahoo Finance website. Based on the research results, it's known that Bank Mandiri has the highest investment risk and BCA has the lowest investment risk. Based on these results, it can be suggested that investors who like risk can choose to invest in Bank Mandiri shares, and those who don't like risk can invest in BCA shares.
Keywords: GARCH, EGARCH, TGARCH, Volatility, VaR
Investasi merupakan suatu kegiatan penanaman modal pada sebuah perusahaan atau proyek berupa aset atau dana untuk jangka waktu tertentu dengan tujuan memperoleh imbal hasil yang lebih besar (Tyas et al., 2019). Bursa Efek Indonesia (2020) menyatakan bahwa salah satu jenis investasi yang banyak diminati investor yaitu investasi pada bursa saham karena dapat memberikan tingkat keuntungan yang menarik. Namun jika keuntungan yang diharapkan semakin tinggi, maka risiko yang mungkin ditanggung juga akan semakin tinggi. Oleh karena itu, penting bagi seorang investor untuk mengetahui tingkat risiko investasi agar dapat mengambil keputusan investasi yang tepat. Tsay (2013) menyatakan bahwa ukuran risiko yang umum digunakan yaitu value at risk (VaR). VaR merupakan estimasi kerugian maksimum dalam bentuk persen atau sejumlah uang selama periode waktu dan selang kepercayaan tertentu (Dwipa, 2016). Salah satu metode yang dapat digunakan untuk menghitung VaR yaitu
metode varians kovarians, dengan menggunakan nilai volatilitas (Damiyanti et al., 2018).
Volatilitas merupakan jarak fluktuasi pada return aset finansial, yang erat kaitannya dengan risiko (Danielsson, 2011). Kemungkinan risiko investasi pada suatu saham akan semakin besar apabila nilai volatilitasnya semakin besar (Maruddani and Purbowati, 2009). Terdapat beberapa model pendekatan yang dapat digunakan untuk memprediksi volatilitas seperti model autoregressive conditional heteroscedasticity (ARCH) yang diperkenalkan oleh Robert F. Engle pada tahun 1982, dan dapat digunakan untuk mengatasi keheterogenan varians. Model ARCH kurang efektif jika digunakan pada orde yang lebih tinggi sehingga pada tahun 1986 dikembangkan oleh Bollerslev menjadi model generalized autoregressive conditional heteroscedastisity (GARCH). Model ARCH dan GARCH memiliki respons volatilitas yang simetris terhadap good news dan bad news. Namun, pada beberapa data finansial terdapat respons volatilitas yang bersifat asimetris
sehingga model GARCH dikembangkan lagi menjadi model GARCH asimetris yaitu model exponential GARCH (EGARCH) yang diperkenalkan oleh Nelson pada tahun 1991 dan model threshold GARCH (TGARCH) yang diperkenalkan oleh Zakoian pada tahun 1994.
Model GARCH, TGARCH, dan EGATCH banyak diterapkan oleh para peneliti untuk meramalkan volatilitas pada data finansial, seperti pada data harga saham. Puspitasari (2020) menyatakan bahwa investasi saham yang banyak diincar investor adalah investasi pada sektor perbankan, karena memiliki peran penting dalam pembangunan negara dan diawasi oleh Otoritas Jasa Keuangan (OJK). Terdapat beberapa saham yang merupakan saham unggulan atau saham blue chip yang banyak diminati investor dan tercatat sebagai saham utama pada papan pencatatan di Bursa Efek Indonesia (BEI) seperti BRI, BCA, dan Bank Mandiri. Agar dapat mengambil keputusan investasi yang tepat, maka perlu dilakukan perhitungan risiko terhadap saham tersebut. Oleh karena itu, tujuan dari penelitian ini adalah untuk melakukan peramalan volatilitas dan estimasi VaR dengan menggunakan model GARCH, TGARCH, atau EGARCH pada saham BRI, BCA, dan Bank Mandiri.
Data yang digunakan dalam penelitian ini merupakan data sekunder yaitu data harga penutupan saham BRI, BCA, dan Bank Mandiri periode 25 Mei 2005 sampai 21 Mei 2021 selama hari aktif (Senin sampai Jumat) dengan jumlah data masing-masing saham yaitu 3.967 data yang diperoleh melalui website Yahoo Finance. Analisis data dilakukan dengan menggunakan software R 3.6.2 untuk meramalkan volatilitas dan software Excel 2007 untuk menghitung VaR. Adapun langkah-langkah analisis data dalam penelitian ini adalah sebagai berikut.
-
1. Menghitung Return
Nilai return dihitung berdasarkan persamaan (Tsay, 2013):
-
^t=ln(^=lnpt-lnpt-ι (1)
iT-I'
dengan Pt merupakan harga aset pada periode ke-t serta ln adalah logaritma natural.
-
2. Analisis Deskriptif Data Return
Analisis deskriptif dilakukan untuk menegaskan secara empiris ciri khas dari
4.
data finansial dengan menghitung nilai skewness dan kurtosis.
-
3. Pemeriksaan Kestasioneran Data Return Pemeriksaan kestasioneran data return
dilakukan dengan mengamati plot data return, grafik correlogram ACF dan PACF data return, serta uji Augmented Dickey
Fuller (ADF) dengan hipotesis uji digunakan yaitu (Tsay, 2013):
H 0:β = 0 (data tidak stasioner) H1. β < 0 (data stasioner).
Statistik uji yang digunakan adalah:
tv = ^sE^
dengan S E (β) merupakan standar penduga β. Kriteria keputusan
yang
(2)
error yang
digunakan adalah hipotesis H0 ditolak jika |tp| > Za atau p-value < a (Tsay, 2013).
2
Jika data return belum stasioner, maka
dilakukan proses differencing hingga diperoleh data yang stasioner.
Pemeriksaan pada Return Kuadrat
Model GARCH, TGARCH, dan EGARCH baik diterapkan apabila terdapat korelasi serta efek ARCH pada return. Ada tidaknya autokorelasi dapat diketahui melalui uji Ljung-Box dengan hipotesis uji yang digunakan yaitu (Tsay, 2013):
H0: p1 = p2 = ... = pl= 0 (tidak
terdapat korelasi)
H1: ∃ ph ≠ 0;h = 1,2,3,..., /(terdapat korelasi),
serta statistik uji yang digunakan yaitu:
2
Qω = T(T + 2)∑Uι⅛ (3)
dengan l menyatakan banyaknya lag yang diuji dan ph merupakan autokorelasi pada lag h. Kriteria keputusan yang digunakan adalah hipotesis H0 ditolak jika Q(I) > Xa atau jika nilai p-value < a (Tsay, 2013). Sedangkan ada tidaknya efek ARCH dapat diketahui melalui uji ARCH-Lagrange Multiplier (ARCH-LM) dengan hipotesis uji yang digunakan yaitu (Tsay, 2013):
H0 :a1 = a2 = a3 =...= am = 0 (tidak terdapat efek ARCH)
H1: ∃ai ≠ 0 (terdapat efek ARCH).
Statistik uji yang digunakan yaitu:
f _ (SSR0-SSRi)Zm ,.
SSR1∕(T-2m-1) '
dengan SSR0 = ∑t=m+1(at-ω)2, ω = (1∕P)∑T=1a2 merupakan mean dari a2, dan SSR1 = ∑τ=m+1et, dengan et
merupakan residual kuadrat terkecil pada
waktu t. kriteria keputusan yang digunakan adalah hipotesis H0 ditolak jika nilai F > X2(a) atau p-value < a (Tsay, 2013). Jika tidak terdapat korelasi dan efek ARCH, maka proses berhenti atau tidak dimodelkan dengan model GARCH. Sedangkan jika terdapat korelasi dan efek ARCH, maka proses dilanjutkan ke langkah 5.
5. Estimasi Parameter Model GARCH
6.
7.
8.
Estimasi parameter model GARCH dilakukan dengan menggunakan data return dan software R.
Pemilihan Model GARCH
Model GARCH yang dipilih adalah model yang signifikan atau memiliki nilai p-value < 0,05 berdasarkan estimasi parameter
model GARCH pada langkah 5 dan memiliki nilai AIC terkecil. AIC dihitung berdasarkan rumus (Tsay, 2013):
AIC= -Oog(Iikelihood) + 2“ . (5)
Uji Sign dan Size Bias
Uji sign dan size bias dilakukan untuk mengetahui apakah terdapat efek asimetris pada data return. Adapun hipotesis uji yang digunakan yaitu (Tsay, 2013):
Ho: V1— $2 — φ3 =...= φm — 0 (residual bersifat simetris)
H1: ∃ φi ≠ 0; i — 1,2,3,^,m (residual bersifat asimetris). Sedangkan statistik uji yang digunakan
yaitu:
τ-, SSRo/k
F — ------------.
SSR1∕(T-k-1)
(6)
Kriteria keputusan yang digunakan adalah hipotesis H0 ditolak jika nilai F > Xm(O)
atau p-value < a (Tsay, 2013). Jikatidak terdapat efek asimetris, maka volatilitas dimodelkan dengan menggunakan model GARCH. Persamaan model GARCH(m,s) yaitu (Tsay, 2013):
σt =ao + ∑mιatal-i + ∑fiβ∣σl2-∣.(7) Jika terdapat efek asimetris, maka dilanjutkan ke langkah 8.
Estimasi Parameter Model TGARCH dan
EGARCH
Estimasi parameter model TGARCH dan
EGARCH dilakukan menggunakan data return dan software R. Persamaan model EGARCH(m,s) yaitu (Tsay, 2013):
ln(σ2) — α0 + ∑m1 a -t- +
l 1 σ(t-0
∑t=ιβjln(σ2-j) (8)
dengan γi merupakan parameter leverage effect at-i. Sedangkan persamaan model TGARCH(m,s) yaitu (Tsay, 2013): σt = ao + ∑"ι(α1 + γlN2-l)a2-l +
∑' -^σ. (9)
dengan Nt_t merupakan indikator dari at-i negatif atau disebut juga variabel dummy yaitu:
N-. = {1jkaat-i < 0 t-i (.0; jika at_j ≥ 0. 9. Peramalan Volatilitas
Peramalan volatilitas dilakukan pada empat belas periode berikutnya yaitu 24 Mei 2021 sampai 10 Juni 2021 dengan menggunakan model yang terpilih.
-
10. Estimasi Value at Risk (VaR)
Estimasi VaR dilakukan dengan menggunakan holding period satu hari, tingkat kepercayaan 95%, dan diasumsikan investasi awal yang digunakan yaitu Rp10.000.000,00. Persamaan yang digunakan untuk menghitung VaR yaitu (Jorion, 2007):
VaR —W0.(Za.√k.σ) (10)
dengan W0 merupakan investasi awal, Za merupakan kuantil distribusi normal standar, σ merupakan volatilitas, dan k merupakan holding period.
-
3. HASIL DAN PEMBAHASAN
-
3.1 Menghitung Return
-
Tabel 1. Data Pertama dan Kedua Harga
Penutupan Saham BRI, BCA, dan Bank Mandiri
|
BRI (Rp) |
BCA (Rp) |
Bank Mandiri (Rp) | |
|
Data Pertama |
275 |
1.637,5 |
830,89 |
|
Data Kedua |
280 |
1.650 |
830,89 |
Sumber: Data diolah, 2021
Data Return dihitung dengan menggunakan persamaan (1). Berdasarkan Tabel 1 serta dengan memisalkan riA,riB,ric secara berturut-turut merupakan return ke-i saham BRI, BCA, dan Bank Mandiri, maka contoh perhitungan nilai return pertama saham BRI, BCA, dan Bank Mandiri yaitu:
riA = In^ = 0,018,
r1B — In 1.650 — 0,007, dan
1B 1.637,5 ,
^1C
830,891479
= ln
830,891479
= 0.
Dengan cara yang sama, dapat dihitung nilai return untuk t = 2,3,4,^,3.967 dari masing-masing saham.
Statistika deskriptif data return BRI, BCA, dan Bank Mandiri dapat dilihat pada Tabel 2.
Tabel 2. Statistika Deskriptif Data Return BRI, BCA, dan Bank Mandiri
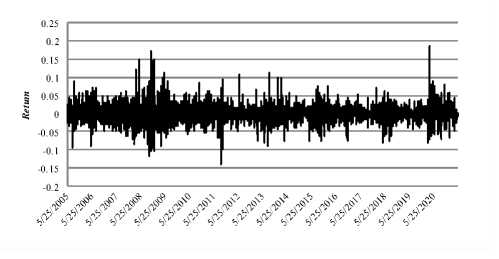
Gambar 1. Plot Data Return BRI
|
Statistika Deskriptif |
Return BRI |
Return BCA |
Return Bank Mandiri |
|
Minimum |
-0,140582 |
-0,106222 |
-0,156842 |
|
Maksimum |
0,186412 |
0,159849 |
0,182322 |
|
Rata-rata |
0,000668 |
0,000748 |
0,000491 |
|
Deviasi Standar |
0,024912 |
0,019424 |
0,024827 |
|
Skewness |
0,330636 |
0,079374 |
0,228580 |
|
Kurtosis |
4,549173 |
4,910327 |
5,053740 |
Sumber: Data diolah, 2021
0.2
0.15
0.1
0.05
0
-0.05
-0.1
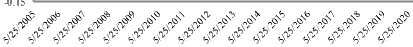
Gambar 2. Plot Data Return BCA
Berdasarkan Tabel 2 diketahui saham Bank Mandiri memiliki nilai return minimum paling rendah dibandingkan saham lainnya dan saham BRI memiliki nilai return maksimum paling tinggi dibandingkan saham lainnya. Nilai rata-rata return dari masing-masing saham bernilai positif yang menunjukkan adanya peluang mendapatkan keuntungan. Nilai deviasi standar return saham BRI, BCA, dan Bank Mandiri tidak sama dengan nol yang menunjukkan bahwa setiap data pada masing-masing saham tidak sama atau terdapat kecenderungan setiap data berbeda (heterogen). Nilai skewness masing-masing saham lebih besar dari nol menunjukkan distribusi dari return memiliki ekor kanan lebih panjang daripada ekor kiri distribusinya. Hal ini berarti terdapat adanya ketidaksimetrisan pada data. Kemudian nilai kurtosis masing-masing saham lebih dari tiga yang menunjukkan adanya excess kurtosis sehingga diketahui bahwa return dari ketiga saham tidak berdistribusi normal yang merupakan stylized fact return data finansial.
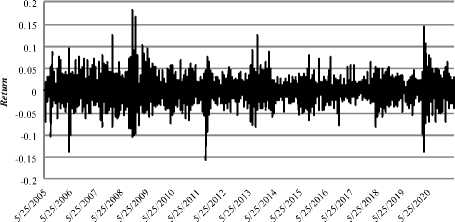
Gambar 3. Plot Data Return Bank Mandiri
Berdasarkan Gambar 1, 2, dan 3 dapat diamati bahwa data return BRI, BCA, dan Bank Mandiri sangat fluktuatif dari waktu ke waktu serta menunjukkan adanya volatility clustering. Berdasarkan plot data return di atas, dapat diperkirakan bahwa data return stasioner dalam mean karena return bergerak pada kisaran nilai mean. Pemeriksaan kestasioneran terhadap data return juga dapat diamati melalui grafik correlogram nilai ACF dan PACF yang dapat dilihat pada Gambar 4, 5, dan 6.
Pemeriksaan kestasioneran melalui plot data return dapat dilihat secara berturut-turut pada Gambar 1, 2, dan 3.
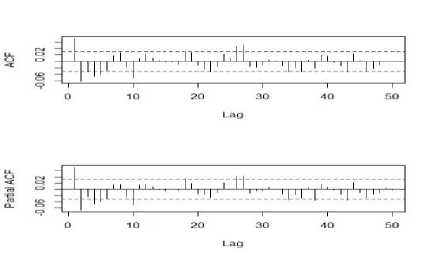
Gambar 4. Grafik Correlogram Nilai ACF dan PACF Data Return BRI
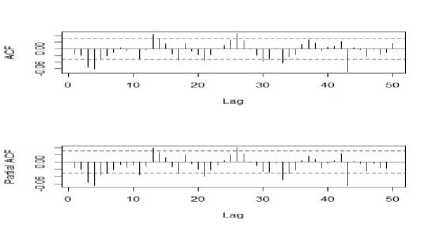
Gambar 5. Grafik Correlogram Nilai ACF dan PACF Data Return BCA
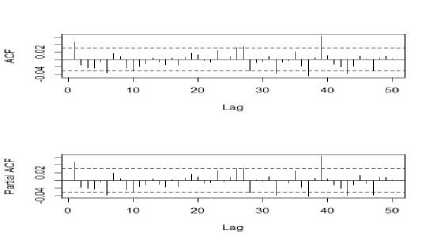
Gambar 6. Grafik Correlogram Nilai ACF dan PACF Data Return Bank Mandiri
Berdasarkan Gambar 4, 5, dan 6 dapat diamati bahwa hanya beberapa lag yang keluar dari garis Bartlett sehingga mengindikasikan data return sudah stasioner. Namun untuk lebih memastikan bahwa data return sudah stasioner, maka dilakukan uji ADF. Adapun hasil uji ADF dengan menggunakan statistik uji pada persamaan (2) dapat dilihat pada Tabel 3.
Tabel 3 Hasil Uji ADF
|
Return BRI |
Return BCA |
Return Bank Mandiri | |
|
p-value |
0,01 |
0,01 |
0,01 |
Sumber: Data diolah, 2021
Berdasarkan Tabel 3 diketahui return masing-masing saham memiliki nilai p-value sebesar 0,01. Hal ini berarti data return saham BRI, BCA, dan Bank Mandiri sudah stasioner.
Ada tidaknya autokorelasi dapat diketahui melalui uji Ljung-Box dengan menggunakan statistik uji pada persamaan (3). Sedangkan ada tidaknya efek ARCH, dapat diketahui melalui uji ARCH-LM dengan menggunakan statistik uji pada persamaan (4). Dengan menggunakan software R, diperoleh nilai Q dan nilai F yang disajikan pada Tabel 4.
Tabel 4. Hasil Uji Ljung-Box dan Uji ARCH-LM
|
Uji |
BRI |
BCA |
Bank Mandiri |
|
Q |
2,2 × 10-16 |
2,2 × 10-16 |
2,2 × 10-16 |
|
F |
2,2 × 10-16 |
5,764 × 10-12 |
2,2 × 10-16 |
Sumber: Data diolah, 2021
Tabel 4 menunjukkan hasil uji Ljung-Box dengan taraf signifikansi 5% masing-masing saham memiliki nilai p-value 2,2 × 10-16 sehingga tidak cukup bukti untuk menerima H0. Sehingga, dapat disimpulkan terdapat korelasi pada masing-masing saham. Uji ARCH-LM dari masing-masing saham menghasilkan nilai p-value < 0,05 yang berarti tidak cukup bukti untuk menerima H0. Dengan demikian berarti terdapat efek ARCH pada data return kuadrat saham BRI, BCA, dan Bank Mandiri. Karena terdapat korelasi dan efek ARCH, maka volatilitas dimodelkan dengan menggunakan model GARCH.
Estimasi parameter model GARCH (m,s) dilakukan dengan menggunakan software R dan data return. Adapun hasil estimasi parameter model GARCH untuk masing-masing saham dapat diamati melalui Tabel 5, 6, dan 7.
Tabel 5. Estimasi Parameter Model GARCH(m, s) Saham BRI
|
Model |
Para meter |
Estimasi Parameter |
p-value |
|
GARCH(1,1) |
«0 |
1,208× 10-5 |
6,33 × 10-8 |
|
«1 |
9,260 × 10-2 |
2 × 10-16 | |
|
β1 |
8,885 × 10-1 |
2 × 10-16 | |
|
GARCH(1,2) |
«0 |
1,620 × 10-5 |
9,54 × 10-8 |
|
«1 |
1,288× 10-1 |
2,22 × 10—16 | |
|
β |
4,173 × 10-1 |
0,000161 | |
|
½ |
4,287× 10-1 |
2,49 × 10-5 | |
|
GARCH(2,1) |
«0 |
1,207 × 10-5 |
1,65 × 10-6 |
|
«1 |
9,257 × 10-2 |
2,94 × 10-8 | |
|
«2 |
1 × 10-8 |
1 | |
|
β1 |
8,885 × 10-1 |
2 × 10-16 | |
|
GARCH(2,2) |
«0 |
1,620× 10-5 |
0,013090 |
|
«1 |
1,288× 10-1 |
2,67 × 10-8 | |
|
«2 |
1 × 10-8 |
1 | |
|
β1 |
4,173 × 10-1 |
0,283007 | |
|
β2 |
4,287× 10-1 |
0,203660 |
Sumber: Data diolah, 2021
Tabel 6. Estimasi Parameter Model GARCH(m, s) Saham BCA
|
Model |
Para meter |
Estimasi Parameter |
p-value |
|
GARCH(1,1) |
«0 |
6,279 × 10-6 |
1,10 × 10-5 |
|
«1 |
8,469 × 10-2 |
2,04 × 10—14 | |
|
β1 |
8,995 × 10-1 |
2 × 10-16 | |
|
GARCH(1,2) |
«0 |
8,190 × 10-6 |
8,65 × 10-6 |
|
«1 |
1,136× 10-1 |
9,77 × 10—15 | |
|
β1 |
4,514 × 10-1 |
5,62 × 10-6 | |
|
β2 |
4,139× 10-1 |
9,35 × 10-6 | |
|
GARCH(2,1) |
«0 |
6,303 × 10-6 |
0,000673 |
|
«1 |
8,487 × 10-2 |
4,47 × 10—10 | |
|
«2 |
1 × 10-8 |
1 | |
|
β1 |
8,992 × 10-1 |
2 × 10-16 | |
|
GARCH(2,2) |
«0 |
8,190 × 10-6 |
NA |
|
«1 |
10,746 |
2 × 10-16 | |
|
«2 |
1 × 10-8 |
NA | |
|
β1 |
4,514× 10-1 |
NA | |
|
β |
4,139 × 10-1 |
NA |
Sumber: Data diolah, 2021
Tabel 7. Estimasi Parameter Model GARCH(m, s) Saham Bank Mandiri
|
Model |
Para meter |
Estimasi Parameter |
p-value |
|
GARCH(1,1) |
«0 |
1,815 × 10-5 |
5,07 × 10-6 |
|
«1 |
1,019× 10-1 |
2,22 × 10—16 | |
|
β1 |
8,676 × 10-1 |
2 × 10-16 | |
|
GARCH(1,2) |
«0 |
2,378× 10-5 |
2,15 × 10-6 |
|
«1 |
1,394 × 10-1 |
2 × 10-16 | |
|
β1 |
3,761 × 10-1 |
3,32 × 10-5 | |
|
β2 |
4,442 × 10-1 |
1,24 × 10-7 | |
|
GARCH(2,1) |
«0 |
1,820 × 10-5 |
0,000256 |
|
«1 |
1,021 × 10-1 |
6,091 × 0—10 | |
|
«2 |
1 × 10-8 |
1 | |
|
β1 |
8,673 × 10-1 |
2 × 10-16 | |
|
GARCH(2,2) |
«0 |
2,378× 10-5 |
0,00153 |
|
«1 |
1,394 × 10-1 |
3,26 × 10—12 | |
|
«2 |
1 × 10-8 |
1 | |
|
β1 |
3,761 × 10-1 |
0,06011 | |
|
β2 |
4,442 × 10-1 |
0,00700 |
Sumber: Data diolah, 2021
Pemilihan model GARCH dilakukan dengan memilih model yang signifikan dan memiliki nilai AIC terkecil. Nilai AIC dihitung dengan menggunakan persamaan (5) dan menggunakan software R. Berdasarkan hasil estimasi parameter model GARCH pada subbab sebelumnya, diketahui hanya model GARCH(1,1) dan GARCH(1,2) yang signifikan karena memiliki nilai p-value < 0,05. Oleh karena itu, perhitungan nilai AIC hanya dilakukan terhadap model tersebut. Adapun nilai AIC return saham BRI, BCA, dan Bank Mandiri secara berturut-turut dapat dilihat pada Tabel 8,9, dan 10.
Tabel 8. Nilai AIC Model GARCH(m,s) Data Return BRI
|
Model |
AIC |
|
GARCH(1,1) |
-4,800689 |
|
GARCH(1,2) |
-4,802390 |
Sumber: Data diolah, 2021
Tabel 9. Nilai AIC Model GARCH(m, s) Data Return BCA
|
Model |
AIC |
|
GARCH(1,1) |
-5,297732 |
|
GARCH(1,2) |
-5,300462 |
Sumber: Data diolah, 2021
Tabel 10. Nilai AIC Model GARCH(m,s) Data Return Bank Mandiri
|
Model |
AIC |
|
GARCH(1,1) |
-4,796578 |
|
GARCH(1,2) |
-4,799436 |
Sumber: Data diolah, 2021
Tabel 8, 9, dan 10 menunjukkan bahwa nilai AIC terkecil di antara model GARCH yang ditinjau untuk saham BRI, BCA, dan Bank Mandiri adalah model GARCH(1,2). Oleh karena itu, model yang dipilih di sini adalah model GARCH(1,2). Adapun persamaan model GARCH(1,2) saham BRI, BCA, dan Bank Mandiri berdasarkan model GARCH pada persamaan (7) dan nilai parameter α0,α1,β1, dan β2 model GARCH(1,2) pada Tabel 5, 6, dan 7 secara berturut-turut adalah:
σ⅛ = 0,0000162+ 0,1288c⅛-1 + 0,4173σ2-1 + -0,4287σ2-2
σ⅛ = 0,00000819+ 0,1136c⅛-1 + 0,4514σ2-1 + 0,4139σt2-2
σt2c = 0,00002378+ 0,1394α2-1 + 0,3761σt2-1 + 0,4442σt2-2.
Uji sign dan size bias dilakukan dengan menggunakan statistik uji pada persamaan (6) dan dengan menggunakan software R. Adapun hasil uji sign dan size bias dari model GARCH(1,2) saham BRI, BCA, dan Bank Mandiri dapat dilihat pada Tabel 11,12, dan 13.
Tabel 11. Uji Sign dan Size Bias Model GARCH(1,2) Saham BRI
|
t-statistic |
p-value |
Sig | |
|
Sign Bias |
1,2943314 |
0,1956264 | |
|
Negative Size Bias |
0,2736724 |
0,7843507 | |
|
Positive Size Bias |
0,8351571 |
0,4036796 | |
|
Join Effect |
2,5962503 |
0,4581473 |
Sumber:Data diolah, 2021
Tabel 12. Uji Sign dan Size Bias Model GARCH(1,2) Saham BCA
|
t-statistic |
p-value |
Sig | |
|
Sign Bias |
1,9022245 |
0,05721428 |
* |
|
Negative Size Bias |
0,8734421 |
0,38247508 | |
|
Positive Size Bias |
1,2010190 |
0,22981564 | |
|
Join Effect |
7,0619783 |
0,06994833 |
* |
Sumber:Data diolah, 2021
Tabel 13. Uji Sign dan Size Bias Model GARCH(1,2) Saham Bank Mandiri
|
t-statistic |
p-value |
Sig | |
|
Sign Bias |
1,03804872 |
0,29931073 | |
|
Negative Size Bias |
1,80547981 |
0,07107553 |
* |
|
Positive Size Bias |
0,05908017 |
0,95289123 | |
|
Join Effect |
9,40678344 |
0,02434399 |
** |
Sumber:Data diolah, 2021
Tabel 11 menunjukkan saham BRI tidak bersifat asimetris karena tidak terdapat parameter dari uji sign dan size bias yang signifikan. Sehingga peramalan volatilitas saham BRI dimodelkan dengan menggunakan model GARCH(1,2). Hasil uji sign dan size bias saham BCA pada Tabel 12 menunjukkan parameter sign bias signifikan, serta uji sign
dan size bias saham Bank Mandiri pada Tabel 13 menunjukkan bahwa parameter negative size bias signifikan. Oleh karena itu, volatilitas saham BCA dan Bank Mandiri dimodelkan dengan menggunakan model GARCH asimetris.
Estimasi parameter model TGARCH dan EGARCH dilakukan dengan menggunakan software R dan data return. Adapun hasil estimasi parameter model TGARCH dan EGARCH data return saham BCA dan Bank Mandiri dapat diamati melalui Tabel 14 dan 15.
Tabel 14. Estimasi Parameter Model EGARCH dan TGARCH Return BCA
|
Model |
Parame ter |
Estimasi Parameter |
p-value |
|
EGARCH(1,1) |
“o |
-0,209030 |
0 |
|
αι |
-0,043150 |
0,000006 | |
|
A |
0,972625 |
0 | |
|
Y1 |
0,174414 |
0 | |
|
EGARCH(1,2) |
“o |
-0,271973 |
0,016275 |
|
“1 |
-0,056156 |
0 | |
|
A |
0,544845 |
0 | |
|
A |
0,419495 |
0 | |
|
ħ |
0,236644 |
0 | |
|
EGARCH(2,1) |
“o |
-0,144013 |
0 |
|
“1 |
-0,038693 |
0,071278 | |
|
“2 |
-0,002572 |
0,904616 | |
|
A |
0,981054 |
0 | |
|
K |
0,303212 |
0 | |
|
Y2 |
-0,166389 |
0 | |
|
EGARCH(2,2) |
“0 |
-0,140772 |
0 |
|
“1 |
-0,038776 |
0,063581 | |
|
“2 |
-0,001591 |
0,940888 | |
|
A |
0,999990 |
0 | |
|
A |
-0,018512 |
0 | |
|
K |
0,303848 |
0 | |
|
K2 |
-0,169948 |
0,001500 | |
|
TGARCH(1,1) |
“0 |
4,890× 10-4 |
2,85×10-10 |
|
“1 |
9,047× 10-2 |
2 × 10-16 | |
|
A |
9,085× 10-1 |
2 × 10-16 | |
|
K1 |
3,041× 10-1 |
1,92×10-7 | |
|
TGARCH(1,2) |
“0 |
0,0006368 |
2,98×10-10 |
|
“1 |
0,1205156 |
2 × 10-16 | |
|
A |
0,4738161 |
5,57×10-7 | |
|
A |
0,4049610 |
6,25×10-6 | |
|
K1 |
0,3083516 |
6,49×10-8 | |
|
TGARCH(2,1) |
“0 |
4,901× 10-4 |
2,86×10-10 |
|
“1 |
9,058× 10-2 |
2 × 10-16 | |
|
“2 |
1 × 10-8 |
NA | |
|
A |
9,084× 10-1 |
2 × 10-16 | |
|
K1 |
3,039× 10-1 |
1,93×10-7 | |
|
K |
3,340× 10-1 |
NA | |
|
TGARCH(2,2) |
“0 |
6,367× 10-4 |
2,98×10-10 |
|
“1 |
1,205× 10-1 |
2 × 10-16 | |
|
“2 |
1 × 10-8 |
NA | |
|
A |
4,738× 10-1 |
5,57×10-7 | |
|
A |
4,050× 10-1 |
6,25×10-6 | |
|
K1 |
3,084× 10-1 |
6,49×10-8 | |
|
K |
2,653× 10-1 |
NA |
Sumber: Data diolah, 2021
Tabel 15. Estimasi Parameter Model EGARCH dan TGARCH Data Return Saham Bank Mandiri
|
Model |
Para meter |
Estimasi Parameter |
p-value |
|
EGARCH(1,1) |
«0 |
-0,240873 |
0 |
|
aι |
-0,044513 |
0,000017 | |
|
β1 |
0,967064 |
0 | |
|
y1 |
0,177182 |
0,000006 | |
|
EGARCH(1,2) |
«0 |
-0,307281 |
0,004190 |
|
«1 |
-0,062306 |
0 | |
|
βι |
0,507072 |
0 | |
|
β2 |
0,450842 |
0 | |
|
y1 |
0,237967 |
0 | |
|
EGARCH(2,1) |
«0 |
-0,167975 |
0 |
|
«1 |
-0.069838 |
0,001501 | |
|
«2 |
0,028018 |
0,208789 | |
|
β1 |
0,976913 |
0 | |
|
y1 |
0,274321 |
0 | |
|
r≈ |
-0,133026 |
0 | |
|
EGARCH(2,2) |
«0 |
-0,163675 |
0 |
|
«1 |
-0,070255 |
0,001403 | |
|
«2 |
0,029459 |
0,192709 | |
|
β1 |
1 |
0 | |
|
β2 |
-0,022495 |
0 | |
|
y1 |
0,274859 |
0 | |
|
y2 |
-0,137203 |
0,000031 | |
|
TGARCH(1,1) |
«0 |
0,0008483 |
1,2 × 10-6 |
|
«1 |
0,0959997 |
2 × 10-16 | |
|
β1 |
0,8926063 |
2 × 10-16 | |
|
y1 |
0,2923670 |
1,4 × 10-7 | |
|
TGARCH(1,2) |
«0 |
0,001068 |
2,18× 10-7 |
|
«1 |
0,128751 |
2 × 10-16 | |
|
β1 |
0,388240 |
6,84 × 10-5 | |
|
β2 |
0,470613 |
5,92 × 10-7 | |
|
y1 |
0,297978 |
1,38× 10-7 | |
|
TGARCH(2,1) |
«0 |
8,5231 × 10-4 |
1,12 × 10-6 |
|
«1 |
9,626 × 10-2 |
2 × 10-16 | |
|
«2 |
1 × 10-≡ |
NA | |
|
β1 |
8,922 ×10-1 |
2 × 10-16 | |
|
y1 |
2,912 ×10-1 |
1,51 × 10-7 | |
|
y2 |
1,457 × 10-1 |
NA | |
|
TGARCH(2,2) |
«0 |
1,068 × 10-3 |
2,18× 10-7 |
|
«1 |
1,288 × 10-1 |
2 × 10-16 | |
|
«2 |
1 × 10-8 |
NA | |
|
β1 |
3,882 ×10-1 |
6,84 × 10-5 | |
|
β2 |
4,706 × 10-1 |
5,92 × 10-7 | |
|
y1 |
2,980 × 10-1 |
1,38× 10-7 | |
|
y2 |
8,474 × 10-2 |
NA |
Sumber: Data diolah, 2021
Pemilihan model dilakukan dengan memilih model yang signifikan dan memiliki nilai AIC terkecil. Berdasarkan hasil estimasi parameter model TGARCH dan EGARCH pada subbab sebelumya diketahui hanya model EGARCH(1,1),EGARCH(1,2),TGARCH(1,1), dan TGARCH(1,2) yang signifikan. Oleh karena itu, perhitungan nilai AIC hanya akan dilakukan terhadap model tersebut. Adapun nilai AIC model TGARCH dan EGARCH return BCA serta Bank Mandiri disajikan pada Tabel 16 dan 17.
Tabel 16. Nilai AIC Model EGARCH dan TGARCH Return BCA
|
Model |
AIC |
|
EGARCH(1,1) |
-5,2985 |
|
EGARCH(1,2) |
-5,3021 |
|
TGARCH(1,1) |
-5,2471 |
|
TGARCH(1,2) |
-5,2388 |
Sumber: Data diolah, 2021
Tabel 17. Nilai AIC Model EGARCH dan TGARCH Return Bank Mandiri
|
Model |
AIC |
|
EGARCH(1,1) |
-5,2985 |
|
EGARCH(1,2) |
-4,8016 |
|
TGARCH(1,1) |
-4,7838 |
|
TGARCH(1,2) |
-4,7836 |
Sumber: Data diolah, 2021
Tabel 16 dan 17 menunjukkan bahwa nilai AIC terkecil di antara model EGARCH dan TGARCH return saham BCA dan Bank Mandiri terdapat pada model EGARCH(1,2). Oleh karena itu, model yang dipilih di sini adalah model EGARCH(1,2). Berdasarkan model EGARCH pada persamaan (8) dan nilai parameter a0,a1,y1,β1 dan β2 model EGARCH(1,2) pada Tabel 14 dan 15, maka model EGARCH(1,2) data return saham BCA dan Bank Mandiri secara berturut-turut adalah:
ln(σ⅛) = -0,271973- 0,056156
∣αt-1∣+0,236644αt-1 °t-1
0,544845 ln(σt2-1)
+0,419495 ln(σ2-2)
ln(σ2c) = -0,307281 - 0,062306
lαt-1l+0,237967αt-1 °t-1
0,507072 ln(σ2-1) + 0,450842 ln(σ2-2).
Peramalan volatilitas dilakukan untuk 14 periode berikutnya yaitu dari 24 Mei 2021 sampai 10 Juni 2021. Volatilitas saham BRI diramalkan dengan menggunakan model GARCH(1,2), sedangkan volatilitas saham BCA dan Bank Mandiri diramalkan dengan menggunakan model EGARCH(1,2).
Peramalan volatilitas dilakukan dengan
menggunakan software R. Adapun hasil peramalan volatilitas saham BRI, BCA, dan Bank Mandiri pada 14 periode berikutnya dapat dilihat pada Tabel 18 serta secara grafis dapat dilihat pada Gambar 7.
Tabel 18. Hasil Peramalan Volatilitas
|
Waktu |
Nilai Volatilitas BRI |
Nilai Volatilitas BCA |
Nilai Volatilitas Bank Mandiri |
|
24 Mei 2021 |
0,01592795 |
0,01313 |
0,02175 |
|
25 Mei 2021 |
0,01638232 |
0,01354 |
0,02064 |
|
26 Mei 2021 |
0,01647781 |
0,01360 |
0,02134 |
|
27 Mei 2021 |
0,01671901 |
0,01381 |
0,02120 |
|
28 Mei 2021 |
0,01688914 |
0,01395 |
0,02144 |
|
31 Mei 2021 |
0,01708209 |
0,01412 |
0,02150 |
|
1 Juni 2021 |
0,01725771 |
0,01427 |
0,02165 |
|
2 Juni 2021 |
0,01743364 |
0,01443 |
0,02175 |
|
3 Juni 2021 |
0,01760256 |
0,01459 |
0,02187 |
|
4 Juni 2021 |
0,01776791 |
0,01474 |
0,02197 |
|
7 Juni 2021 |
0,01792845 |
0,01489 |
0,02208 |
|
8 Juni 2021 |
0,01808497 |
0,01503 |
0,02218 |
|
9 Juni 2021 |
0,01823735 |
0,01518 |
0,02228 |
|
10 Juni 2021 |
0,01838587 |
0,01532 |
0,02238 |
Sumber: Data diolah, 2021
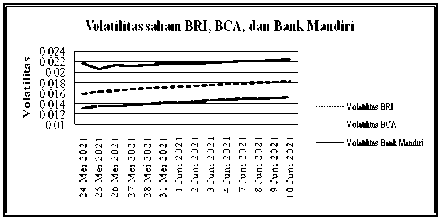
Gambar 7. Peramalan Volatilitas saham BRI, BCA, dan Bank Mandiri
Berdasarkan hasil peramalan volatilitas saham BRI, BCA, dan Bank Mandiri pada Tabel 18 serta grafik hasil peramalan volatilitas pada Gambar 7 diketahui bahwa volatilitas saham BRI, BCA, dan Bank Mandiri cenderung mengalami peningkatan dari periode ke periode. Hasil peramalan volatilitas saham BRI berkisar dari 0,01592795 sampai 0,01838587, BCA berkisar dari 0,01313 sampai 0,01532, dan Bank Mandiri berkisar dari 0,02064 sampai 0,02238. Kisaran nilai tersebut menunjukkan bahwa volatilitas tertinggi terdapat pada saham Bank Mandiri dan volatilitas terendah terdapat pada saham BCA.
Perhitungan VaR dilakukan dengan menggunakan persamaan (10), pada holding period satu hari, dan selang kepercayaan 95%. Pada penelitian ini diasumsikan bahwa dana
investasi yang digunakan sebesar Rp10.000.000,00. Estimasi VaR dilakukan dengan menggunakan software excel. Berdasarkan hasil peramalan volatilitas pada Tabel 18, diperoleh estimasi VaR yang disajikan pada Tabel 19 dan disajikan dalam bentuk grafis pada Gambar 8.
Tabel 19. Estimasi Value at Risk (VaR) saham BRI, BCA, dan Bank Mandiri
|
Waktu |
Var Saham BRI |
VaR Saham BCA |
VaR Saham Bank Mandiri |
|
24 Mei 2021 |
Rp262.811,18 |
Rp216.645,00 |
Rp358.875,00 |
|
25 Mei 2021 |
Rp270.308,28 |
Rp223.410,00 |
Rp340.560,00 |
|
26 Mei 2021 |
Rp271.883,87 |
Rp224.400,00 |
Rp352.110,00 |
|
27 Mei 2021 |
Rp275.863,67 |
Rp227.865,00 |
Rp349.800,00 |
|
28 Mei 2021 |
Rp278.670,81 |
Rp230.175,00 |
Rp353.760,00 |
|
31 Mei 2021 |
Rp281.854,49 |
Rp232.980,00 |
Rp354.750,00 |
|
1 Juni 2021 |
Rp284.752.22 |
Rp235.455,00 |
Rp357.225,00 |
|
2 Juni 2021 |
Rp287.655,06 |
Rp238.095,00 |
Rp358.875,00 |
|
3 Juni 2021 |
Rp290.442,24 |
Rp240.735,00 |
Rp360.855,00 |
|
4 Juni 2021 |
Rp293.170,52 |
Rp243.210,00 |
Rp362.505,00 |
|
7 Juni 2021 |
Rp295.819,43 |
Rp245.685,00 |
Rp364.320,00 |
|
8 Juni 2021 |
Rp298.402,01 |
Rp247.995,00 |
Rp365.970,00 |
|
9 Juni 2021 |
Rp300.916,28 |
Rp250.470,00 |
Rp367.620,00 |
|
10 Juni 2021 |
Rp303.366,86 |
Rp252.780,00 |
Rp369.270,00 |
|
Rata-rata |
Rp285.422,63 |
Rp236.421,43 |
Rp358.278,46 |
Sumber: Data diolah, 2021
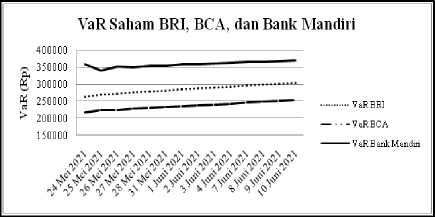
Gambar 8. Estimasi VaR saham BRI, BCA, dan Bank Mandiri
Berdasarkan Tabel 19 estimasi nilai VaR saham BRI pada tanggal 24 Mei 2021 yaitu Rp262.811,18. Hal ini berarti apabila investor berinvestasi pada saham BRI sebesar Rp10.000.000,00, pada holding period satu hari, dan selang kepercayaan 95%, maka terdapat keyakinan sebesar 95% kerugian maksimum yang ditanggung investor sebesar Rp262.811,18 atau dengan kata lain terdapat kemungkinan sebesar 5% kerugian yang ditanggung oleh investor lebih dari Rp262.811,18. VaR saham BRI berkisar dari Rp262.811,18 sampai Rp303.366,86 dengan nilai VaR terendah terdapat pada tanggal 24 Mei 2021 dan VaR tertinggi terdapat pada tanggal 10 Juni 2021. Saham BRI memiliki nilai rata-rata VaR sebesar Rp285.422,63.
Hal yang sama juga bisa dijelaskan untuk nilai VaR BCA dan Bank Mandiri untuk setiap periodenya cenderung mengalami peningkatan dari periode ke periode yang juga dapat diamati melalui Gambar 8. Berdasarkan nilai rata-rata VaR dari masing-masing saham diketahui bahwa saham Bank Mandiri memiliki tingkat risiko investasi tertinggi dan BCA memiliki tingkat risiko investasi terendah. Sehingga dapat disarankan bagi investor yang menyukai risiko dapat memilih berinvestasi pada saham Bank Mandiri dan bagi investor yang tidak menyukai risiko dapat berinvestasi pada saham BCA.
Setelah dilakukan analisis terhadap data harian harga penutupan saham BRI, BCA, dan Bank Mandiri, diperoleh simpulan yaitu:
Di antara model GARCH, TGARCH, dan EGARCH, model terbaik untuk memodelkan volatilitas saham BRI adalah model GARCH(1,2). Sedangkan model yang digunakan untuk memodelkan volatilitas saham BCA dan Bank Mandiri adalah model EGARCH(1,2).
Hasil peramalan volatilitas saham BRI, BCA, dan Bank Mandiri pada empat belas periode berikutnya yaitu 24 Mei 2021 sampai 10 Juni 2021 cenderung menunjukkan peningkatan dari periode ke periode. Volatilitas tertinggi terdapat pada saham Bank Mandiri dan volatilitas terendah terdapat pada saham BCA.
Berdasarkan hasil estimasi nilai VaR dengan menggunakan tingkat kepercayaan 95%, holding period satu hari, dan investasi awal Rp10.000.000,00, estimasi nilai VaR dari saham BRI, BCA, dan Bank Mandiri cenderung mengalami peningkatan dari periode ke periode. Rata-rata VaR dari saham BRI, BCA, dan Bank Mandiri secara berturut-turut adalah Rp285.422,63, Rp260.944,59, dan Rp383.745,15. Hal ini berarti saham Bank Mandiri memiliki tingkat risiko investasi tertinggi dan BCA memiliki tingkat risiko investasi yang terendah.
Mengingat dalam penelitian ini diketahui saham BCA dan Bank Mandiri bersifat asimetris sehingga dimodelkan dengan menggunakan model GARCH asimetris. Berdasarkan nilai AIC dan hasil estimasi parameter, diketahui model EGARCH merupakan model yang lebih baik
dibandingkan model TGARCH untuk meramalkan volatilitas saham BCA dan Bank Mandiri. Oleh karena itu, dapat disarankan bagi penelitian selanjutnya yang ingin meramalkan volatilitas data harga saham yang bersifat asimetris dapat menggunakan model EGARCH. Selain itu, disarankan juga bagi penelitian selanjutnya untuk membandingkan model EGARCH dengan model asimetris lainnya.
DAFTAR PUSTAKA
Bursa Efek Indonesia. 2020. Saham.
https://www.idx.co.id/produk/saham/.
Diakses 16 Agustus 2020 (21:21 WITA).
Damiyanti, D. P. D., Dharmawan, K., and Harini, L. P. I. 2018. Perhitungan Value at Risk dengan Penduga Volatilitas Stokastik Heston. E-Jurnal Matematika, 7(4), pp. 317–321.
Danielsson, J. 2011. Financial Risk Forecasting. United Kingdom: John Wiley and Sons.
Dwipa, N. M. S. 2016. Peramalan Value at Risk Menggunakan Metode GARCH. Buletin Ilmiah Mat. Stat, dan Terapannya, 5(2), pp. 267–276.
Jorion, P. 2007. Value at Risk the New Benchmarkfor Managing Financial Risk.United States of America:McGraw-Hill Companies.
Maruddani, D. A. I., and Purbowati, A. 2009. Pengukuran Value at Risk pada Aset Tunggal dan Portofolio dengan Simulasi Monte Carlo. Jurnal Media Statistika, 2(2), pp. 93–104.
Peraturan Otoritas Jasa Keuangan Nomor 56/POJK.03/2016, Pub. L. No. 3 (2016).
Puspitasari, I. 2020. Banyak Diburu Asing, Ini Rekomendasi Analis untuk Saham Perbankan.
https://investasi.kontan.co.id/news/banyak-diburu-asing-ini-rekomendasi-analis-untuk-saham-perbankan. Diakses 5 Oktober 2020, (10;15 WITA).
Tsay, R. S. 2013. An Introduction to Analysis of Financial Data with R. Canada: John Wiley and Sons.
Tyas, M. D. P., Maruddani, D. A. I., and Rahmawati, R. 2019. Perhitungan Value at Risk dengan Pendekatan Threshold Autoregressive Conditional
Heteroscedasticity-Generalized Extreme Value. Jurnal Media Statistika, 12(1), pp. 73–85.
208
Discussion and feedback