PENGGUNAAN METODE PROJECTED UNIT CREDIT DAN AGGREGATE COST PADA ASURANSI PENSIUN NORMAL

E-Jurnal Matematika Vol. 10(4), November 2021, pp. 209-214

DOI: https://doi.org/10.24843/MTK.2021.v10.i04.p344

ISSN: 2303-1751

PENGGUNAAN METODE PROJECTED UNIT CREDIT DAN AGGREGATE COST PADA ASURANSI PENSIUN NORMAL

Sarah Veronica Hutabalian^1§, I Nyoman Widana², Luh Putu Ida Harini³

¹Program Studi Matematika, FMIPA, Universitas Udayana [Email: [email protected]] ²Program Studi Matematika, FMIPA, Universitas Udayana [Email: [email protected]] ³Program Studi Matematika, FMIPA, Universitas Udayana [Email: [email protected]]

^§Corresponding Author

ABSTRACT

Employees can be referred to as company assets because they play an important role in the progress and decline of a company. So the company can protect the welfare of employees when their age can no longer be productive, one of which is to include employees in pension fund insurance. This study aims to calculate and compare the normal contributions that participants must pay using the methods Projected Unit Credit and Aggregate Cost. The calculation of normal contributions using the method Projected Unit Credit uses the present value of the pension benefits divided by the length of service. The Method Aggregate Cost uses the present value of the pension benefits minus the accumulatedfunds and divided by the term annuity. The result of this research is that the normal contribution amount using the method Projected Unit Credit is lower in the payments in the first years than using the method Aggregate Cost. The Method contribution Projected Unit Credit increases significantly as the length of service period and the method Aggregate Cost increases slowly but increases sharply as the retirement age approaches.

Keywords: Projected Unit Credit, Aggregate Cost, Normal Cost, Pension

• 1.    PENDAHULUAN

Karyawan merupakan para tenaga kerja yang menjalankan setiap aktivitas dan tugas dalam suatu perusahaan. Pengertian karyawan secara umum adalah manusia atau orang yang menggunakan tenaga dan kemampuannya untuk mendapat balasan jasa berupa pendapatan, baik berupa uang maupun dalam bentuk lainnya dari perusahan atau pemberi kerja. Karyawan dapat disebut menjadi aset perusahaan mengingat produktivitas dari karyawan sangat berpengaruh terhadap kemajuan atau kemunduran suatu perusahan (Oktiani, 2013). Oleh karena itu, karyawan memiliki peran penting sehingga perusahaan perlu untuk melindungi dan menjamin kesejahteraanya.

Ada beberapa cara untuk mengoptimalkan produktivitas karyawan, salah satunya adalah menjamin kesejahteraannya saat karyawan sudah tidak dapat produktif lagi. Setelah mengikutsertakan karyawan pada program asuransi dana pensiun, diharapkan karyawan tidak akan merasa khawatir akan

kesejahteraannya pada usia pensiun atau kemungkinan terburuk yang dapat terjadi. Pada lain pihak dampak positif yang dapat diterima oleh perusahaan apabila memberikan asuransi kepada karyawan adalah dapat meringankan keuangan perusahaan dengan mengalihkan risiko karyawan kepada perusahaan asuransi. Tentu perusahaan juga akan berharap program asuransi pensiun ini akan meningkatkan loyalitas dari karyawannya terhadap perusahaan dan dapat juga menjadi salah satu cara untuk membalas jasa para pekerja yang telah mengabdikan hidupnya untuk kemajuan perusahaan.

Pengertian dari asuransi dana pensiun yaitu salah satu produk asuransi yang bertujuan untuk memberikan jaminan kepada pemegang polisnya saat mencapai usia pensiun. Dana pensiun didapatkan dari iuran yang dibayarakan secara rutin oleh karyawan. Pembayarannya dapat dilakukan setiap bulan maupun setiap tahun. Dana pensiun tersebut akan dikelola serta dijalankan oleh suatu lembaga sehingga peserta bisa memperoleh manfaat pensiun secara rutin

maupun sekaligus. Terdapat beberapa jenis-jenis pensiun yaitu pensiun normal, pensiun cacat, pensiun meninggal dunia atau sering disebut dengan pensiun janda atau duda, dan pensiun dipercepat (Nainggolan, 2019).

Banyaknya karyawan yang memiliki berbagai macam risiko membuat perusahaan harus mulai memperhitungkan pembayaran anuitas untuk karyawan pada asuransi dana pensiun yang akan dikeluarkan. Untuk itu akan dilakukan perhitungan dana pensiun menggunakan metode perhitungan aktuaria. Secara garis besar metode perhitungan dikelompokan menjadi dua, yaitu Accrued Benefit Cost Method dan Projected Benefit Cost Method (SPA-DP 3.02). Metode yang tergolong dalam kelompok Accrued Benefit Cost Method adalah Unit Credit Method dan Projected Unit Credit. Sedangkan yang merupakan kelompok dari Projected Benefit Cost Method terdiri dari Aggregate Cost Method, Entry Age Normal Method, Attained Age Normal Method, Individual Level Premium (Futami, 1994).

Berdasarkan hal tersebut penulis tertarik untuk menggunakan metode Projected Unit Credit dan metode Aggregate Cost pada pensiun normal untuk perhitungan iuran normal peserta, dengan judul “Penggunaan metode Projected Unit Credit dan Aggregate Cost pada asuransi pensiun normal”

• 2.    METODE PENELITIAN

Jenis data yang digunakan pada penelitian ini adalah data kuantitatif. Data ini merupakan data sekunder yaitu gaji Pegawai Negri Sipil golongan III/a yang terbaru diperoleh dari Peraturan Pemerintah Republik Indonesia tentang Peraturan Gaji Pegawai Negri Sipil dan menggunakan bantuan dari Tabel Mortalita Taspen 2012.

Langkah-langkah yang akan dilakukan dalam penelitian ini adalah sebagai berikut:

• 1.    Menghitung akumulasi gaji selama setahun.

• 2.    Menghitung besar manfaat pensiun, adapun perhitungan manfaat pensiun dengan menggunakan gaji setahun terakhir:

B_r=k(r-y)s_r-₁          (3)

dengan:

k: persen proporsi gaji untuk perhitungan dana pensiun

• r: usia saat pensiun normal y: usia saat masuk kerja

s_r-1: besar gaji selama setahun terakhir

• 3.    Menghitung nilai sekarang manfaat pensiun atau Present value of future benefit (PVFB). Present value of future benefit merupakan nilai sekarang dari manfaat pensiun yang nantinya akan diterima oleh peserta program pensiun setelah mencapai usia pensiun. Pembayaran manfaat pensiun akan dilakukan hingga peserta meninggal. Menurut Winklevoss (1993), perhitungan nilai manfaat pensiun yang akan diterima saat peserta berusia r tahun dengan (y ≤ x < r) dapat dirumuskan menjadi:

^r (PVFB)_x = BrV^r~^xa_τr-_xp_x      (4)

dengan:

B_r    = manfaat pensiun

v^r-x = faktor diskonto

a_r    = anuitas awal seumur hidup

_r-xp_x = peluang seseorang akan tetap

hidup hingga usia r tahun.

Agar mempermudah perhitungan akan dicari terlebih dahulu nilai faktor diskonto

Vⁿ menggunakan suku bunga i yaitu:

1 vⁿ =------

^V (1 + i)ⁿ

(5)

Selanjutnya mencari anuitas awal seumur hidup menggunakan:

a_r = 1 + vp_r + V² ₂P_r +—       ⁽⁶⁾

dengan

^r+n

nPr     f                ⁽⁷⁾

^r

• 4.    Menghitung besaran iuran normal (NC) menggunakan metode Projected Unit Credit dan Aggragate Cost.

• a.    Projected Unit Credit

Projected Unit Credit menggunakan pembagian manfaat pensiun yang akan didapat peserta pensiun apabila bekerja hingga mencapai usia pensiun normal dengan total dari masa kerja. Manfaat pensiun pada saat peserta berusia x dihitung dari manfaat pensiun yang akan datang saat memasuki usia pensiun normal yaitu r tahun, manfaat pensiun saat usia mencapai pensiun normal dibagi secara merata pada setiap tahun dari masa kerja. Iuran normal metode Projected Unit Credit dapat dihitung menggunakan rumusan sebagai berikut (Oktiani,2013):

1

^r(NC)x = —— ^r(PVFB)x

^{(r — y)}

1

7Z     ^Br V   ¹—xPx ^ar

^{(r —} y)

(8)

• b.    Aggragate Cost

Pada metode aggregate cost, iuran normal biasa disebut premi yang menyatakan besarnya keseluruhan yang dibayarkan oleh peserta. Perhitungan nilai iuran normal metode aggregate cost di dapat dari nilai sekarang manfaat pensiun, jumlah akumulasi dana pada tahun ke n yang disimbolkan dengan F_n dan anuitas awal sementara. F didapatkan dari jumlah akumulasi dana selama setahun dibagi P_x atau dapat dituliskan sebagai berikut (Dickson, 2009):

Dana Akhir Tahun       (9)

=       Px

Dana akhir tahun merupakan perhitungan dana dari iuran normal pada tahun sebelumnya, dana akhir tahun pada tahun sebelumnya dan beserta bunganya. Atau dapat dituliskan sebagai berikut:

(NC)_n-1 + (DanaAkhir Tahun)_n-1

+ ((NC)n-ι

+ (Dana Akhir Tahun)_n-1) * i

maka F dapat kita tuliskan menjadi

(NC_n-₁ +Dana AkhirTahun_l^₁) * (1 +i) F =--ⁿ^

Px

dengan:

(10)

(NC)_n-1: iuran normal pada tahun n — 1

Iuran normal metode aggregate cost yang harus dibayarkan dapat dituliskan sebagai berikut (Futami, 1994):

^rNC_x =

B_rv^{r x}_r-xp_xa_r-F a —r x:n\

(11)

dengan:

a_χ-∣ = anuitas awal berjangka n tahun

Perhitungan anuitas awal berjangka n tahun menggunakan

ax:n\= 1 + ^vPx + ^v2 2Px+-    ⁽¹²⁾

⁺vⁿ~∖-ιPx

• 5.    Menghitung     kewajiban     aktuaria

menggunakan metode Projected Unit credit.

Kewajiban aktuaria atau actuarial liability (AL) ialah besar dana dari program pensiun untuk pembayaran manfaat pensiun selanjutnya yang seharusnya sudah terkumpul. Menurut Oktiani (2013) kewajiban aktuaria bisa diibaratkan juga dengan cadangan manfaat. Kewajiban aktuaria dapat dituliskan sebagai berikut (Oktiani,2013):

^T(AL)x =(^y) ^-“-Jx^  (13)

• 6.    Membandingkan hasil dari kedua metode tersebut.

• 3.    HASIL DAN PEMBAHASAN

Berikut penerapan penggunaan metode Projected Unit Credit dan Aggregate Cost pada contoh kasus

Contoh Kasus

Seorang karyawan Pegawai Negri Sipil golongan III/a mulai menjadi peserta asuransi dana pensiun saat berumur 24 tahun dan terhitung pensiun pada usia 56 tahun (r = 56). Didapat lama masa kerja (n) yaitu 32 tahun. Menggunakan perhitungan akumulasi gaji selama setahun terakhir (s_r-1) yang diterima sebesar Rp 30.952.800,-. Perhitungan tingkat suku bunga (i) yang digunakan sebesar 5% dan (k') yaitu 4,75%. Akan ditentukan iuran yang harus dibayarkan oleh karyawan tersebut.

• 3.1    Besar Manfaat Pensiun (B_r)

Berdasarkan penggunaan persamaan (3) dapat dicari manfaat pensiun yang akan didapat berdasarkan jumlah gaji selama setahun terakhir dan k yaitu sebesar 4.75% sebagai berikut:

B_r = k(r -y)s_r-1

= 4.75%(56- 24)(30952800)

= 47048256

Jadi, besar manfaat pensiun yang akan didapatkan saat peserta memasuki usia pensiun yaitu sebesar Rp 47.048.256,

• 3.2    Nilai sekarang dari manfaat yang akan
  
  didapat (PVFB)

Akan dilakukan perhitungan anuitas awal seumur hidup terlebih dahulu. Menggunakan bantuan Tabel Mortalita Taspen 2012 dan menggunakan suku bunga, i = 5% anuitas awal seumur hidup didapatkan sebagai berikut:

0-56 = (

V⁵‰ + ^ ⁵⁶⁺¹^ 56+1 + ∙ + ^w

v^xl_x

=(

»56 + ^56+1 + - + »115

^56

»56

)

)

»56

= 13,42

didapat nilai anuitas yaitu 13,42. Selanjutnya faktor diskonto yang diperoleh sebagai berikut:

1

Vⁿ = ------ "    (1 + iΓ

1

°²'-

Diperoleh iuran normal yang peserta harus bayarkan mengunakan metode Projected Unit Credit yaitu sebesar Rp 3.776.169,576

2. Menggunakan metode Aggregate Cost

Sebelum menghitung iuran menggunakan metode Aggregate Cost akan dihitung nilai F menggunakan (9) namun pada iuran normal pembayaran pertama digunakan asumsi nilai F adalah 0 karna pada pembayaran pertama belum terdapat dana akhir tahun atau dapat dituliskan sebagai berikut:

_ (0)(1 + 5%)

^F= 0.99943333

= 0

Setelah didapatkan anuitas dan faktor diskonto, maka berdasarkan (4) nilai sekarang dari manfaat pensiun didapatkan sebagai berikut:

Selanjutnya akan dihitung nilai anuitas awal berjangka (O_t.^) sebagai berikut:

^r (PVFB)_x = B_rυ^r-^χa_rr-xp_x =B56^^56-24⅛656-24½4 = (47048256)(0,209866) _{λ     λ} (90151,26∖

^(13,42) (98879,987

= 120837426,4

Jadi, nilai sekarang manfaat pensiun yang diperoleh untuk % = 24 adalah Rp 120.837.426,-

∕v^xl_x + v ^ax:n|    l

= (^v2⁴l

^24

^x+‰ + ∙→v^x+n-‰-1 ^^xIx

)

' 24+ V²⁴⁺¹l24+1 + ∙ + V^24+32-1l24+32-1

V²‰             ,

_-

^56

»24

570176,70-2116,65

30659,50

•)

• 3.3    Menghitung Iuran Normal

Perhitungan iuran normal atau biasa disebut premi yang akan peserta harus bayarkan. Perhitungannya akan menggunakan metode Projected Unit Credit dan Aggregate Cost sebagai berikut:

• 1.    Menggunakan metode Projected Unit Credit

Berdasarkan persamaan (8) perhitungan menggunakan metode Projected Unit Credit adalah sebagai berikut:

1 ^r∖NC)_x = ₇----~B_rV

^x (r-y)

1

= (56- 24)^B5^6V

r-x r-x

^px^αr

^{56 2}4^α56 56-24^p24

(47048256) (0.209866) (13.42) (0.911724036)

32

= 3776169,576

= 16,32

Didapatkan nilai anuitas awal berjangka yaitu 16,32 dan berdasarkan persamaan (11) perhitungan iuran menggunakan metode Aggregate Cost sebagai berikut:

_r^^ _ B_rV   r-x^px^ar ^F

^x          α —i

x:n|

(1209837426-0)

16.32

= 7403240,695

Maka didapat iuran yang harus dibayarkan oleh peserta pada pembayaran pertama mengunakan metode Aggregate Cost yaitu Rp 7.403.240,695.

Pembayaran iuran setiap tahun menggunakan metode Projected Unit Credit dan metode Aggregate Cost oleh peserta membentuk grafik iuran seperti pada Gambar 3.1.

0

Iuran Aggregate Cost

Iuran Projected Unit Credit

20000000

10000000

0 3 6 9 12151821242730

PEMBAYARAN TAHUN KE-N

Gambar 3.1. Iuran Normal

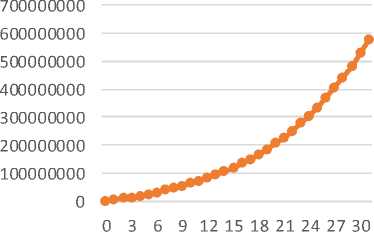
Gambar 3.2. Kewajiban Aktuaria

Pada Gambar 3.1 terlihat grafik iuran dari metode Projected Unit Credit dan metode Aggregate Cost. Garis Iuran normal pada tahun pertama mengguanakan metode Projected Unit Credit menghasilkan iuran yang lebih rendah dibandingkan menggunakan metode Aggregate Cost hingga di pertengahan masa kerja. Pada tahun selanjutnya iuran normal dengan metode Projected Unit Credit menghasilkan iuran yang lebih tinggi. Iuran dengan metode Projected Unit Credit terus meningkat secara signifikan seiring bertambahnya masa kerja. Sehingga dengan bertambahnya usia dan mendekati usia pensiun semakin meningkat pula iuran normal yang peserta harus bayarkan. Peningkatan iuran normal menggunakan metode Projected Unit Credit dapat dilihat pada grafik dengan garis berwarna merah.

Sedangkan iuran normal menggunakan metode Aggregate Cost menunjukan peningkatan yang lambat, namun menjelang memasuki usia pensiun iuran normal mengalami kenaikan yang tajam.

• 3.4    Menghitung Kewajiban Aktuaria

Kewajiban aktuaria dalam metode Projected Unit Credit akan dicari menggunakan persamaan (13) kewajiban aktuaria didapatkan sebagai berikut:

(24-24)

^(AL)* = (56-24)^β56^r     56-24P≡6⅛6

0

= —120837462

= 0

Didapatkan kewajiban aktuaria pada tahun pertama yaitu Rp 0,-. Perhitungan kewajiban aktuaria selengkapnya diilustrasika pada grafik pada Gambar 3.2.

Pada tahun pertama kewajiban aktuaria yang didapat adalah Rp 0,- disebabkan karena lama masa kerja saat perhitungan berlangsung yaitu 0 tahun. Kewajiban aktuaria terus meningkat seiring menambahnya masa kerja. Sedangkan pada metode Aggregate Cost tidak terdapat kewajiban aktuaria. Menurut Standar Praktik Aktuaria menyatakan nilai kewajiban aktuaria dianggap sama dengan nilai sekarang manfaat pensiun.

• 4.    KESIMPULAN DAN SARAN

  • 4.1    Kesimpulan

Iuran normal menggunakan metode Projected Unit Credit menghasilkan iuran yang lebih rendah pada tahun-tahun pertama dibandingkan dengan metode Aggregate Cost. Iuran normal dengan penggunaan metode Projected Unit Credit terus meningkat secara signifikan seiring meningkatnya masa kerja. Sedangkan penggunaan metode Aggregate Cost mengalami peningkatan yang cenderung lambat.

• 4.2    Saran

Berdasarkan penelitian yang telah dilakukan, saran untuk penelitian selanjutnya diharapkan dapat memperhatikan beberapa asumsi seperti kenaikan jabatan, kenaikan gaji, dan asumsi lainnya agar lebih sesuai dengan kasus yang sebenarnya. Sehingga mendapatkan hasil yang lebih tepat dengan kondisi yang ada. Penelitian selanjutnya juga dapat menghitung manfaat pensiun lainnya seperti manfaat pensiun dipercepat, manfaat pensiun cacat dan manfaat pensiun kematian.

DAFTAR PUSTAKA

Dickson, D. C. M., Hardy, M. R., & Waters, H.

• R. (2009). Actuarial Mathematics for Life Contigent Risks. New York: Cambridge University Press.

Futami, T. (1994). Matematika Asuransi Jiwa Bagian II (kedua). Herliyanto, G., penerjemah. Jakarta (ID). Oriental Life Insurance Cultural Development Center. Terjemahan dari: Seimei Hoken Sugaku, Gekan.

Nainggolan, Apnesia Feronika. (2019). Perhitungan Aktuaria untuk Manfaat Pensiun Normal dengan Menggunakan Metode Entry Age dan Individual Level Premium. Skripsi. Medan. Universitas Sumatera Utara.

Oktiani, I. (2013). Perhitungan Aktuaria untuk Manfaat Pensiun Normal Menggunakan Metode Projected Unit Credit dan Entry Age  Normal.  Skripsi.  Bogor. Institut

Pertanian Bogor.

Standar Praktik Aktuaria Dana Pensiun No. 5.01 (SPA-DP No. 5.01).

Winklevoss, H.E. (1993). Pension Mathematics with Numerical Illustrations, Pension Research Council. Philadelphia:University of Penssylvania.

214