PEMODELAN KASUS DIARE DI PROVINSI BALI DENGAN METODE ANALISIS REGRESI SPASIAL
on
E-Jurnal Matematika Vol. 10(2), Mei 2021, pp. 95-102
DOI: https://doi.org/10.24843/MTK.2021.v10.i02.p327
ISSN: 2303-1751
PEMODELAN KASUS DIARE DI PROVINSI BALI DENGAN METODE ANALISIS REGRESI SPASIAL
I.G.A. Diah Sulasih1§, Made Susilawati2, Ni Luh Putu Suciptawati3
1Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: gustiayu973@gmail.com]
2Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: susilawati.made@unud.ac.id]
3Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: suciptawati@unud.ac.id]
§Corresponding Author
ABSTRACT
Diarrhea is a disease that occurs due to changes in the frequency of bowel movements and can cause death. In 2018, 115.889 cases of diarrhea were found in Bali Province. Information on the relationship between locations indicates the spatial effect in the model. Model estimation was done by using spatial regression analysis. This study aims to determine what factors influence diarrhea cases in Bali Province. The results show that the number of diarrhea cases in a district is influenced by the surrounding districts. This is reinforced in the Moran’s I test which shows spatial dependence. In the analysis of the Spatial Error Model (SEM), it was obtained that the value of was 57,69% and the variables that significantly affected diarrhea cases in Bali Province were population density and sanitation facilities
Keywords: Diarrhea, Spatial Regression, SEM
Diare adalah salah satu masalah kesehatan masyarakat di negara-negara berkembang seperti di Indonesia. Tingginya angka kesakitan dan kematian di setiap daerah di Indonesia yang disebabkan oleh diare, menunjukkan diare adalah penyakit endemis dan penyakit potensial kejadian luar biasa (KLB). Kejadian luar biasa terjadi apabila terdapat peningkatan kejadian penyakit/kematian 2 kali lipat atau lebih dibandingkan dengan periode sebelumnya (jam, hari, minggu, bulan, tahun). Di Indonesia terdapat 4.165.789 kasus diare pada tahun 2018 (BPS, 2019).
Kasus diare masih cukup tinggi ditemukan di Provinsi Bali. Menurut Dinas Kesehatan Provinsi Bali, pada tahun 2017 ditemukan sebanyak 114.656 kasus diare, dan sebanyak 11.889 kasus diare pada tahun 2018. Kasus pada tahun 2018 ini meningkat dibandingkan tahun 2017 sebesar 1.233 kasus dikarenakan beberapa kecamatan yang mengalami peningkatan kasus diare di Provinsi Bali.
Penelitian mengenai kasus diare yang dilakukan oleh Sheila (2016) menggunakan pendekatan regresi spasial yaitu General Spatial Model, Spatial Error Model (SEM), dan Spatial Autoregressive (SAR). Faktor-faktor
yang berpengaruh pada persentase kasus diare di kabupaten/kota di Provinsi Jawa Barat pada tahun 2014 adalah proporsi rumah tangga yang tidak memiliki jamban sendiri dengan tangki septik, proporsi rumah sakit terhadap penduduk, proporsi puskesmas keliling terhadap penduduk, dan proporsi posyandu terhadap penduduk. Dari ketiga model tersebut, diperoleh model terbaik menggunakan model SAR. Selanjutnya, Arumsari dan Sutikno (2010) yang meneliti bagaimana model kejadian kasus diare dan faktor apa saja yang memengaruhi kejadian diare di Kabupaten Tuban. Dengan menggunakan pendekatan regresi spasial diperoleh hasil faktor yang memengaruhi kejadian diare yaitu jarak rumah berukuran lebih dari 10 meter dengan pembuangan akhir tinja dan fasilitas air minum baik dengan model regresi OLS, regresi poisson, dan Geographically Weight Poisson Regression.
Tingginya kasus diare pada suatu kecamatan diduga dipengaruhi letak geografis di Bali. Hal ini karena setiap kecamatan yang berdekatan memiliki beberapa karakteristik yang hampir sama. Berdasarkan hal tersebut, model kasus diare di Provinsi Bali kemungkinan memiliki pengaruh efek spasial,
sehingga dibuat dengan menggunakan analisis regresi spasial dengan memerhatikan aspek lokasi.
Regresi spasial adalah teknik statistika yang bertujuan untuk melihat hubungan variabel independen dengan variabel dependen, dengan adanya informasi ruang (spasial) pada data, sehingga dalam menganalisis harus mempertimbangkan efek spasial dari data tersebut (Anselin, 1988). Berdasarkan adanya informasi ruang (spasial), maka model yang dihasilkan adalah model regresi spasial.
Pemodelan spasial merupakan.pemodelan yang menggunakan efek spasial yang berhubungan dengan pendekatan titik dan area yang bertujuan untuk menggambarkan hubungan antara variabel bebas terhadap variabel respon. Efek spasial dapat dibedakan menjadi dua aspek yaitu efek depedensi spasial yang ditunjukkan dengan adanya kemiripan karakteristik antarlokasi yang saling bertetangga dan efek heterogenitas spasial yang menunjukkan adanya keragaman antarlokasi yang bertetangga (LeSage & Pace, 2009). Hubungan antar wilayah digambarkan dalam bentuk matriks pembobot spasial. Matriks pembobot spasial merupakan komponen dasar dari model spasial yang dibentuk berdasarkan peta tematik suatu wilayah dengan melihat persinggungan antar lokasi satu dengan lokasi lainnya. Secara umum, model regresi spasial dapat ditulis
y = pW1y + Xβ+λW2 μ + ε (1) dengan y adalah variabel dependen, p adalah keofisien spasial lag, W1 dan W2 adalah matriks pembobot spasial, X adalah variabel dependen, β adalah parameter koefisien regresi, λ adalah koefisien lag spasial pada error, μ adalah galat (sisaan) yang diasumsikan berautokorelasi, dan ε adalah galat (sisaan). Model regresi spasial yang berkaitan dengan pendekatan area yaitu spatial autoregressive (SAR), spatial error model (SEM), spatial durbin model (SDM), dan spatial autoregressive moving average (SARMA) (Anselin, 1988).
Tujuan dari penelitian ini adalah untuk memodelkan penyebaran kasus diare pada masing-masing kecamatan dengan menggunakan analisis regresi spasial serta untuk mengetahui faktor-faktor apa saja yang signifikan berpengaruh terhadap penyebaran kasus diare di Provinsi Bali.
Jenis data yang digunakan pada penelitian ini adalah data sekunder yang diperoleh dari Badan Pusat Statistik Provinsi Bali dan Dinas Kesehatan Provinsi Bali tahun 2018. Variabel dependen pada penelitian ini yaitu jumlah kasus diare disetiap kecamatan di Provinsi Bali ( K). Variabel independen pada penelitian ini adalah kepadatan penduduk (X1), jumlah sarana air minum (X2 ), jumlah sarana sanitasi (X3) dan persentase tempat makan tidak memenuhi syarat kesehatan (X4) disetiap kecamatan di Provinsi Bali.
Metode Analisis Data
Metode analisis yang digunakan dalam penelitian ini adalah analisis regresi spasial, dengan langkah-langkah sebagai berikut:
-
1. Melakukan eksplorasi data yang disajikan
dalam bentuk peta tematik, untuk mengetahui penyebaran kasus diare.
-
2. Melakukan estimasi parameter regresi
linier
Xi = po + β1Xι 1 + —+ βp- ιxt (p- 1) + εi (2)
Proses penyusunan model regresi diawali dengan melakukan seleksi variabel yang signifikan terhadap model. Seleksi variabel dilakukan dengan menggunakan metode Stepwise.
-
3. Menentukan matriks pembobot spasial ( W). Berdasarkan hubungan antarlokasi akan diperoleh nilai bobot spasial dari masing-masing amatan (lokasi). Bentuk umum matriks pembobot spasial adalah
W1 i W1 2 *,' W1 ^i
W = W2 1 W2 2 ; ‰
-
. Wn 1 Wn 2 Wnn.
Struktur yang mendasari adanya hubungan ketetanggaan dibuat dalam bobot 0 dan 1 (Anselin, 1988). Elemen Wj7- akan bernilai 0 apabila i dan j tidak memiliki hubungan ketetanggaan atau i = j, sebaliknya Wj7 akan bernilai 1 apabila i dan j memiliki hubungan ketetanggaan atau i ≠ j.
-
4. Menyelidiki adanya autokorelasi spasial antarkecamatan sehingga dapat dianalisis menggunakan regresi spasial. Uji yang digunakan adalah Uji Moran’s I. Uji Moran’s I merupakan pengujian statistika untuk mengetahui nilai autokorelasi spasial dan mengidentifikasi suatu lokasi berdasarkan nilai autokorelasi spasial.
Hipotesis yang digunakan dalam Uji
Moran’s I sebagai berikut :
H0:1 = 0 (tidak ada autokorelasi antarlokasi)
H1:1 ≠ 0 (ada autokorelasi antarlokasi)
Statistik uji yang digunakan adalah
_ I-E(I)
h it = √^V)
dengan
. _ ∕n ∑?= ι∑"= ιWi∕¾ i - ¾(¾7 - ¾)∖
= ( W∑^ 1(×l -x)2 )
E(J~) = v ' n-l
Nilai indeks I berada diantara -1
5.
(3)
(4)
(5) dan 1.
6.
Jika I > Iq maka data memiliki autokorelasi positif dan pola mengelompok, sebaliknya jika I < I0 maka data memiliki autokorelasi negatif dan pola menyebar.
Menyelidiki adanya kebergantungan spasial pada lag, error atau keduanya menggunakan uji Lagrange Multiplier (LM). Uji LM digunakan sebagai dasar untuk memilih model regresi spasial yang sesuai oleh data yang digunakan (Anselin, 1988).
-
a. Kebergantungan Spasial pada lag (SAR)
Model SAR terbentuk apabila nilai p ≠ 0 dan A = 0, sehingga diperoleh model umum SAR sebagai berikut:
y = pWly + Xβ + e (6) Hipotesis yang digunakan dalam LMlag untuk model SAR adalah:
H0: p = 0 (tidak ada kebergantungan spasial lag).
Hl: p ≠ 0 (ada kebergantungan spasial lag).
(⅛)
= -----∖ σ , lag ((w1xβ)'M(w1xβ)+τσ2) ( )
b.
CF2
Kriteria keputusan dalam mengambil kesimpulan adalah H0 ditolak jika LMlag > X(a,l) ataup-value < a.
Kebergantungan Spasial pada error (SEM)
Model SEM terbentuk apabila p = 0 dan A ≠ 0, sehingga model umum SEM diperoleh sebagai berikut:
y = Xβ + AW2u + ε (8)
Hipotesis yang digunakan dalam
LMerror untuk model SEM adalah:
H0: A = 0 (tidak ada kebergantungan spasial error).
: ≠ 0 (ada kebergantungan spasial
error).
⅛≤)
LMerror =7^^ (9)
tr ((W2 + W2)W2 )
Kriteria keputusan dalam mengambil
kesimpulan adalah ditolak jika
LMerror > (a,a,l) ataup-value < a.
Melakukan pendugaan parameter dengan metode maksimum likelihood. Pertama
dilakukan pembentukan fungsi likelihood. Mengingat ε~N(0,σ2I) maka ε dapat dinyatakan dalam bentuk fungsi densitas sebagai berikut:
L(ε;σ2) = √⅛exp[-i(εTε)] (10)
Selanjutnya dapat dibentuk fungsi likelihood sebagai berikut:
L (y∖β, 1) =---^lJ e ε) (11)
(2π)2(σ 2)z
dengan
J = | Ω -2 AA |
Bentuk operasi log-likelihood dari
persamaan (11) dinyatakan sebagai berikut:
TL TL
ln L(β,σ2∖y) = --ln(2π) --ln(σ2 )
+ ln | Ω ~zAA∖ -l(ετε)(12) dengan
ε = Ω~2A(Ay- Xβ) B = (I-A W2)
Syarat determinan dari matriks Jacobian terpenuhi yakni ∣Ω~A A∣ > 0, atau secara parsial memenuhi syarat ∖ - ∖ > 0.
Diasumsikan Ω = σ2 I, sehingga bentuk fungsi log-likelihood menjadi : lnL(β, σ2∖y)=-Eln(2π) -
n ln(σ 2 ) + ln∖I-AW2∖
-⅛( τ )) (13)
Dengan memaksimumkan fungsi loglikelihood diperoleh pendugaan parameter β adalah sebagai berikut:
β = ((Xτ - AW2X τ)r(X - AW2X)) - l
(Xτ - AW2 XτTτ (l - AW2)y (14)
-
7. Melakukan pengujian signifikansi parameter. Uji signifikansi parameter bertujuan untuk menyelidiki peranan variabel bebas dalam model. Uji yang
digunakan adalah uji Wald dengan hipotesis sebagai berikut:
Hq ∶ ,A, βj=0 (parameter tidak
signifikan)
H^ ∶ ,λ, βj≠0 (parameter signifikan)
Untuk statistik Uji Wald (Anselin, 1988) adalah sebagai berikut:
W= *se (r )+ (15)
Kriteria dalam pengambilan keputusan yaitu Hq ditolak jika nilai W> Za atau ’ 2
-
V- value <a.
-
8. Menginterpretasikan dan menyimpulkan hasil yang telah diperoleh.
Pada penelitian ini, nilai yang
menunjukkan banyaknya kejadian dari setiap variabel digambarkan dalam sebuah peta tematik. Peta tematik merupakan peta khusus yang menyajikan tema tertentu yang berfungsi untuk menambah informasi, sehingga memudahkan pembaca dalam membaca peta serta memahami informasi mengenai variabel-variabel yang digunakan. Warna kecamatan semakin terang mengindikasikan semakin rendah nilai dari variabel tersebut, dan semakin gelap mengindikasikan bahwa semakin tinggi nilai dari variabel tersebut.
Gambar 1 menunjukkan penyebaran jumlah kasus diare di Provinsi Bali tahun 2018.
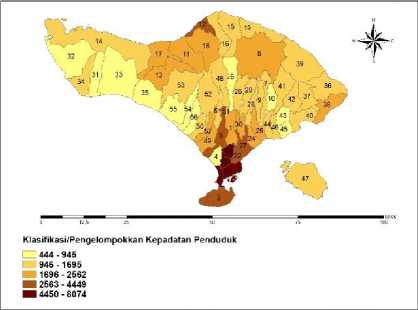
Gambar 1. Peta Penyebaran Jumlah Kasus Diare di Provinsi Bali Tahun 2018
Pada Gambar 1. dapat dilihat bahwa kecamatan yang memiliki tetangga dengan warna sama termasuk dalam kategori yang sama. Kecamatan Selemadeg (54) bertetangga dengan Kecamatan Selemadeg Barat (55) dan Selemadeg Timur (56). Hal ini menunjukkan kecamatan tersebut termasuk dalam jumlah
kasus diare di Provinsi Bali dengan kategori sangat rendah, yaitu dengan skala 444-945 kasus. Selain kecamatan tersebut terdapat 9 kecamatan yang termasuk dalam kategori sangat rendah dengan jumlah kasus diare sangat rendah adalah Kecamatan Kuta Utara dengan 444 kasus.
Selanjutnya, Kecamatan Denpasar Barat (20) bertetangga dengan Kecamatan Kuta (2), Denpasar Selatan (21) dan Denpasar Utara (23). Hal ini menunjukkan kecamatan tersebut termasuk dalam jumlah kasus diare di Provinsi Bali dengan kategori sangat tinggi, yaitu dengan skala 4450-8074 kasus. Selain kecamatan tersebut terdapat Kecamatan Denpasar Barat yang termasuk kategori sangat tinggi dengan jumlah kasus diare sangat tinggi adalah Kecamatan Denpasar Selatan dengan 8.074 kasus.
Berdasarkan Hukum Tobler yang menyatakan bahwa segala sesuatu saling berhubungan dengan yang lainnya, namun sesuatu yang lebih dekat akan lebih berpengaruh dibandingkan dengan yang jauh. Oleh karena itu, secara geografis jumlah kasus diare pada suatu kecamatan sangat dipengaruhi oleh kecamatan yang berada di sekelilingnya, sehingga penelitian ini dapat dianalisis menggunakan analisis regresi spasial.
Estimasi model regresi linier dilakukan dengan bantuan software R i386 4.0.2. Sebelum dilakukan estimasi model regresi linier, terlebih dahulu dilakukan standarisasi data menggunakan standarisasi jenis logaritma natural. Diperoleh estimasi model regresi linier seperti Tabel 1.
Tabel 1. Estimasi Parameter Model Regresi Linier
|
Parameter |
Estimasi Parameter |
^hitung |
p * value |
|
β0 |
1,8410 |
2,048 |
0,0456∗ |
|
βl |
0,2555 |
3,322 |
0,0016∗ |
|
β2 |
0,0673 |
1,722 |
0,091 |
|
β3 |
0,3313 |
2,033 |
0,0038∗ |
|
0,0024 |
0,051 |
0,9596 | |
|
a = 0,05 | |||
|
R2 = 0,5588 | |||
Sumber: data diolah, 2020
Berdasarkan Tabel 1. estimasi model regresi linier yang diperoleh adalah:
̂i=1,8410+0,2555 , + 0,2555 , +
0,3313 , +0,00,24 , , (16)
Selanjutnya melakukan seleksi variabel yang signifikan terhadap model dengan
menggunakan metode Stepwise. Diperoleh variabel bebas yang signifikan dalam model yaitu ^l dan ¾ . Selanjutnya dilakukan estimasi model kembali berdasarkan variabel yang signifikan sebagai berikut.
Tabel 2. Estimasi Parameter Model Regresi Linier
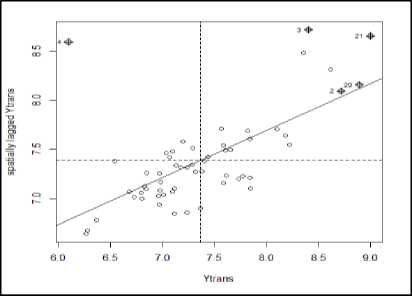
Gambar 2. Moran's I Scatterplot Kasus Diare
|
Parameter |
Estimasi Parameter |
^hitung |
p * value |
|
β0 |
2,108 |
2,048 |
0,0456∗ |
|
β1 |
0,3075 |
3,322 |
0,000∗ |
|
β3 |
0,325 |
2,033 |
0,004∗ |
|
a = 0,05 | |||
|
R2 = 0,5336 | |||
Sumber: data diolah, 2020
Berdasarkan Tabel 2. Diperoleh estimasi model regresi linier adalah sebagai berikut.
̂i = 4,502 + 0,3075 , + 0,325 , (17)
Selanjutnya dilakukan pengujian
kebergantungan spasial untuk menyelidiki terdapat efek spasial pada data sehingga dapat dianalisis dengan regresi spasial. Terlebih dahulu dibentuk matriks pembobot spasial. Dalam penelitian ini matriks pembobot spasial yang digunakan adalah Queen Contiguity karena hubungan ketetanggaan dari metode ini mencakup sisi dan sudut.
Kebergantungan spasial dapat diuji menggunakan Uji Moran’s I dan Uji Lagrange Multiplier. Berdasarkan uji Moran’s I diperoleh nilai probabilitas sebesar 6,864 × 10 9 lebih kecil dari a = 0,05, sehingga keputusan tolak Hq yang berarti bahwa terdapat autokorelasi spasial pada jumlah kasus diare di Provinsi Bali pada tahun 2018. Nilai Moran’s I, yaitu 0,479 lebih besar dari E(I) = -0,018 yang artinya I> Iq . Hal ini menunjukkan terdapat autokorelasi positif, yang artinya kecamatan yang berdekatan memiliki karakteristik yang sama dan memiliki pola mengelompok. Untuk melihat pola pengelompokkan kasus diare, dapat digunakan Moran’s I Scatterplot pada Gambar 2.
Gambar 2. menunjukkan penyebaran variabel jumlah kasus diare terdapat pengelompokkan pada kuadran I (high-high) dan kuadran III (low-low), artinya kecamatan di Provinsi Bali yang memiliki jumlah kasus diare tinggi cenderung berdekatan dengan kecamatan yang memiliki jumlah kasus diare tinggi pula dan kecamatan yang memiliki jumlah kasus diare rendah cenderung berdekatan dengan kecamatan yang memiliki jumlah kasus diare rendah pula. Namun, terdapat juga beberapa kecamatan yang berada pada kuadran II (low-high) dan IV (high-low) yang berarti ada beberapa kecamatan yang memiliki jumlah kasus diare rendah cenderung berdekatan dengan kecamatan yang memiliki jumlah kasus diare tinggi dan kecamatan yang memiliki jumlah kasus diare tinggi cenderung berdekatan dengan kecamatan yang memiliki jumlah kasus diare rendah.
Tabel 3. Uji Lagrange Multiplier
|
Hipotesis Uji |
Nilai Statistik Uji |
Keputusan |
|
H0 : =0 H1 : ≠0 |
LMlag = 2,8519 P- value = 0,0913 P- value <a ∖ = 0,10 |
H0 ditolak. Terdapat kebergantungan spasial pada lag (variabel dependen). |
|
H0 : =0 H1 : ≠0 |
LMerror = 3,1159 P- value = 0,0775 P- value <a ∖ = 0,10 |
H0 ditolak. Terdapat kebergantungan spasial pada error (sisaan). |
|
Hq : = 0 H1 : ≠ 0 |
LMlag, error ∖ = 3,2671 P- value = 0,1952 P- value >a ∖ = 0,10 |
Hq diterima. Tidak terdapat kebergantungan spasial pada lag,error. |
Sumber: data diolah, 2020
Selanjutnya dilakukan uji Lagrange Multiplier untuk menyelidiki ada tidaknya kebergantungan spasial pada lag, error, atau pada keduanya.
Hasil uji Lagrange Multiplier pada Tabel 3. menunjukkan bahwa LM (lag) dan LM (error) signifikan, sehingga dilanjutkan dengan analisis Spatial Autoregressive (SAR) dan Spatial Error Model (SEM).
-
3.4 Pemodelan SAR
Pemodelan SAR dilakukan demgan menguji signifikansi parameter dengan melakukan Uji Wald.
Tabel 4. Uji Wald Model SAR
|
Parameter |
Estimasi |
Wald |
Prob. |
|
P |
0,2615 |
1,7999 |
0,0719 |
|
β0 |
0,9499 |
0,9387 |
0,3479 |
|
βl |
0,2238 |
2,9367 |
0,0033 |
|
β3 |
0,3032 |
2,881 |
0,0039 |
|
a = 0,10 | |||
|
Zq,05 = 1,65 | |||
|
R2 = 0,5638 | |||
|
AIC = 74,775 | |||
Sumber: data diolah, 2020
Tabel 4. menunjukkan bahwa terdapat nilai Wald yang lebih besar dari nilai , = 1,65
dan nilai probabilitas yang kurang dari a = 0,10, sehingga keputusan yang diambil adalah tolak Hq yang berarti Xj dan ^3 signifikan. Ditunjukkan pula pada parameter p memiliki nilai Wald lebih besar dari , =
1,65 dan nilai probabilitas kurang dari = 0,10, sehingga keputusan tolak Hq yang berarti parameter signifikan, dengan kata lain terdapat kebergantungan spasial pada lag.
Diperoleh model sebagai berikut: n
̂i =0,9499+0,2615 ∑ Wtjyj
7=1,i^j
+0,2238 Xli + 0,3032 X 31 (18)
dengan Vi menyatakan jumlah kasus diare pada kecamatan ke-i, Xj menyatakan jumlah kasus diare pada kecamatan ke-j, ^ii menyatakan kepadatan penduduk pada kecamatan ke-i, ^3i menyatakan jumlah sarana sanitasi pada kecamatan ke-i, Wij menyatakan elemen matriks pembobot spasial (Queen Contiguity).
-
3.5 Pemodelan SEM
Pemodelan SEM dilakukan demgan menguji signifikansi parameter dengan melakukan Uji Wald.
Tabel 5. Uji Wald Model SEM
|
Parameter |
Estimasi |
Wald |
Prob. |
|
βo |
1,8377 |
1,8684 |
0,0617 |
|
βl |
0,2418 |
2,9437 |
0,0032 |
|
β3 |
0,3948 |
3,4894 |
0,0005 |
|
λ |
0,3692 |
2,3436 |
0,0191 |
|
a = 0,10 | |||
|
Zq ,05 = 1,65 | |||
|
R2 = 0,5769 | |||
|
AlC = 73,974 | |||
Sumber: data diolah, 2020
Tabel 5. menunjukkan bahwa terdapat nilai Wald yang lebih besar dari nilai , =
1,65 dan nilai probabilitas yang kurang dari a = 0,10, sehingga keputusan yang diambil adalah tolak Hq yang berarti Xj dan ^3 signifikan. Ditunjukkan pula pada parameter λ memiliki nilai Wald lebih besar dari , =
1,65 dan nilai probabilitas kurang dari = 0,10, sehingga keputusan tolak Hq yang berarti parameter signifikan, dengan kata lain terdapat kebergantungan spasial pada sisaan.
Diperoleh model sebagai berikut:
̂ i =1,8377+0,2418Xli + 0,3948 X3i
+0,3692∑ , (19)
dengan Xi menyatakan jumlah kasus diare pada kecamatan ke-i, ^ii menyatakan kepadatan penduduk pada kecamatan ke-i, ^3i menyatakan jumlah sarana sanitasi pada kecamatan ke-i, Ui menyatakan sisaan spasial dari kecamatan ke-i, Uj menyatakan sisaan spasial dari kecamatan ke-j, Wij menyatakan elemen matriks pembobot spasial (Queen Contiguity).
Selanjutnya, akan dibandingkan nilai AIC dan R2 dari model SAR dan SEM.
Tabel 6. Perbandingan Nilai AIC dan R2dari Model
|
Model |
AIC |
R2 |
|
SAR |
74,775 |
56,38% |
|
SEM |
73,974 |
57,69% |
Berdasarkan Tabel 6. dapat dilihat bahwa model SEM memiliki nilai AIC lebih kecil dan nilai R2 lebih besar dari model SAR. Sehingga, model yang sesuai digunakan dalam kasus diare di Provinsi Bali adalah Spatial Error Model (SEM) dengan nilai AIC sebesar 73,974 dan R2 sebesar 57,69%.
Berikut merupakan interpretasi dari model SEM pada persamaan (19) yaitu:
-
1. Koefisien βo = 1,8377
menginterpretasikan bahwa apabila faktor lain dianggap tidak ada, maka rata-rata nilai log natural dari jumlah kasus diare di Provinsi Bali pada tahun 2018 adalah 1,8377 kasus.
-
2. Koefisien βι = 0,2418
menginterpretasikan bahwa jika nilai log natural dari kepadatan penduduk di suatu kecamatan naik satu jiwa/km2, maka dapat menaikkan nilai log natural jumlah kasus diare di kecamatan tersebut sebesar 0,2418 apabila faktor lain dianggap konstan.
-
3. Koefisien β3 = 0,3948
menginterpretasikan bahwa jika nilai log natural dari jumlah sarana sanitasi naik satu sarana, maka dapat menaikkan nilai log natural dari jumlah kasus diare di kecamatan tersebut sebesar 0,3948 apabila faktor lain dianggap konstan.
-
4. Koefisien λ = 0,3692
menginterpretasikan bahwa apabila suatu kecamatan dikelilingi oleh kecamatan lainnya, maka pengaruh dari masing-masing kecamatan yang mengelilinginya dapat diukur sebesar 0,3692 dikali jumlah kasus diare pada kecamatan disekitarnya.
Berdasarkan model SEM pada persamaan (19), diketahui bahwa setiap kecamatan memiliki model yang berbeda-beda berdasarkan matriks pembobot spasial dari kecamatan (I4^ι). Sebagai contoh yaitu Kecamatan Abiansemal, yaitu:
̂Abiansemal = 1,8377
+0,2418 *1 ,Abiansemal
+ 0,3948 ¾ ,Abiansemal + 0,0462Uyiengwi + 0,0462U-Petang + 0,0462U-Denpasar Timur + 0,0462Uoenpasar Utara + 0,0462Upayangan + 0,0462 uSukawati + 0,0462Uubud + 0,0462Uyiarga
Berdasarkan hasil analisis, kedekatan antar kecamatan satu dengan kecamatan lainnya memengaruhi penyebaran kasus diare pada suatu kecamatan, sehingga kondisi geografis di Provinsi Bali memengaruhi jumlah kasus diare. Pada hasil pemodelan kasus diare dengan variabel-variabel yang memengaruhi, diperoleh model Spatial Error Model (SEM) lebih baik karena memiliki AIC = 73,974 lebih kecil dari model Spatial Autoregressive (SAR), dengan kata lain jumlah kasus diare di Provinsi Bali, terdapat kebergantungan spasial antarlokasi pada sisaan. Nilai R2 yang diperoleh dari model SEM sebesar 57,69%. Hal tersebut menunjukkan bahwa model dengan variabel ^l dan X3 mampu menjelaskan kasus diare di Provinsi Bali sebesar 57,69%, sedangkan sisanya sebesar 42,31% dijelaskan oleh variabel lain diluar model.
Adapun faktor-faktor yang memengaruhi jumlah kasus diare di Provinsi Bali, yaitu kepadatan penduduk dan jumlah sarana sanitasi pada setiap kecamatan di Provinsi Bali.
Pada penelitian ini nilai R2 yang diperoleh dari model belum cukup tinggi dikarenakan keterbatasan data yang tersedia pada tahun 2018. Disarankan untuk penelitian selanjutnya peneliti dapat memilih variabel independen dengan baik sehingga variabel independen yang terpilih mampu menjelaskan kasus.
DAFTAR PUSTAKA
Amalia. (2012). Analisis Spasial Kejadian Diare di Wilayah Kerja Puskesmas Panunggangan Kecamatan Pinang Kota Tanggerang Tahun 2009-2011. Universitas Indonesia: Depok.
Anselin, L. (1988). Spatial Econometrics: Method an Models. Kluwer Academic Publishers.
Arumsari, N., & Sutikno. (2010). Permodelan Kejadian Diare dengan Pendekatan Regresi Spasial. Seminar Nasional Pascasarjana X-ITS.
BPS. (2019). Statistik Indonesia 2019. Jakarta: Badan Pusat Statistik Indonesia.
Draper, N. R., & Smith, H. (1998). Applied Regression Analysis: Third Edition.
Canada: John Wiley & Sons, Inc.
Lesage, J. (1999). The Theory and Practice of Spatial Econometrics The Theory.
LeSage, J., & Pace, R. K. (2009). Introduction to Spatial Econometrics. Boca Raton: Taylor & Francis Group.
Sheila, A. N. (2016). Penerapan Regresi Spasial Terhadap Kasus Diare di Provinsi Jawa Barat Tahun 2014. Bogor: Institut Pertanian Bogor.
102
Discussion and feedback