PENERAPAN METODE BAYESIAN VECTOR AUTOREGRESSION DALAM PERAMALAN JUMLAH KUNJUNGAN WISATAWAN CINA KE BALI

E-Jurnal Matematika Vol. 10(2), Mei 2021, pp. 86-94

DOI: https://doi.org/10.24843/MTK.2021.v10.i02.p326

ISSN: 2303-1751

PENERAPAN METODE BAYESIAN VECTOR AUTOREGRESSION

DALAM PERAMALAN JUMLAH KUNJUNGAN WISATAWAN CINA KE BALI

Natasya Widia Putri^1§, I Wayan Sumarjaya², I Gusti Ayu Made Srinadi³

¹Program Studi Matematika, Fakultas MIPA-Universitas Udayana [Email: natasyaputri98@gmail.com] ²Program Studi Matematika, Fakultas MIPA-Universitas Udayana [Email: sumarjaya@unud.ac.id] ³Program Studi Matematika, Fakultas MIPA-Universitas Udayana [Email: srinadi@unud.ac.id]

^§Corresponding Author

ABSTRACT

Bali is one of the regions in Indonesia which has a very rapid development in the tourism sector. This is indicated by the number of foreign tourist visits to Bali. Since 2017, China has shifted Australia's position as the country with the most number of foreign tourist visits to Bali. This study aims to forecast the number of Chinese tourist visits to Bali, Indonesia’s inflation rate, and the CNY to IDR exchange rate for the period June 2019-March 2020 as well as the dynamic relationship between the three variables. This study used the Bayesian Vector Autoregression (BVAR) method with the NormalWishart Prior and compared several lag orders to get the best forecasting results based on the MAPE forecasting criterion. Based on the MAPE forecasting criterion, this study shows the BVAR model with lag 4 produces a very accurate forecasting for the CNY to IDR exchange rate and a good forecasting of the number of Chinese tourist visits to Bali and Indonesia’s inflation rate. The forecast of the number of Chinese tourist visits to Bali, Indonesia’s inflation rate, and the CNY to IDR exchange rate show a stable figure. The impulse response function shows there were shocks in the beginning of the period before finally reaching a stable condition.

Keywords: Bali, Bayesian, Forecasting, Number of Tourist Visits, Vector Autoregressive (VAR).

• 1.    PENDAHULUAN

Menurut Heizer J. dkk (2011) peramalan ialah penggunaan model matematika dalam seni dan ilmu memprediksi kejadian-kejadian pada masa depan menggunakan data masa lalu. Salah satu kegunaan peramalan adalah untuk mereduksi ketidakpastian kejadian pada masa depan. Keputusan yang dibuat akan semakin akurat dan mengakibatkan adanya kesiapan untuk mengantisipasi peristiwa-peristiwa yang tidak diinginkan pada masa yang akan datang.

Salah satu cara untuk mengetahui pengaruh data historis terhadap data yang akan datang agar mampu digunakan dalam peramalan adalah dengan menggunakan analisis deret waktu. Analisis deret waktu (time series analysis) merupakan analisis serangkaian data urutan nilai-nilai variabel tertentu atas beberapa periode waktu (Lütkepohl & Krätzig, 2004). Dalam melakukan analisis deret waktu, diperlukan data yang memiliki interval yang

sama, seperti data harian, mingguan, bulanan, ataupun tahunan. Analisis deret waktu dapat digunakan untuk menganalisis data yang terdiri dari satu variabel (univariate) dan data yang terdiri lebih dari satu variabel (multivariate). Salah satu model yang sering digunakan untuk menganalisis deret waktu multivariat adalah model vector autoregession (VAR). Metode VAR adalah model deret waktu yang dapat digunakan untuk memodelkan dan meramalkan lebih dari satu variabel secara simultan.

Menurut Gujarati (2004) keunggulan dari metode VAR antara lain: (1) bentuk model yang sederhana, artinya tidak perlu khawatir dalam menentukan antara variabel endogen dan variabel eksogen, dalam model ini semua variabel adalah variabel endogen; (2) estimasi model VAR sederhana yaitu bisa menggunakan metode kuadrat terkecil (MKT); (3) hasil peramalan yang diperoleh dari metode ini lebih

Putri, N.W., I W. Sumarjaya, I G.A.M. Srinadi baik dibandingkan dengan model simultan kompleks lainnya.

Gujarati (2004) menyatakan bahwa salah satu tantangan terbesar dalam metode VAR adalah pemilihan lag yang tepat. Ketika variabel terlalu banyak dengan lag yang panjang, dapat mengakibatkan timbulnya parameter dalam jumlah yang besar. Kemudian apabila parameter dalam jumlah yang besar dan jumlah observasi terbatas, maka akan terjadi over-parameterization.      Selain      over

parameterization, masalah lain yang dapat timbul akibat terlalu banyak variabel adalah bentuk model VAR yang menjadi kompleks mengakibatkan sering timbulnya masalah kolinearitas (Sumara & Kusdarwati, 2017). Metode    Bayesian    VAR    mampu

menggabungkan informasi historis dan apriori sehingga dapat mengatasi permasalahan overparameterization dan masalah kolinearitas. Oleh karena itu, penggunaan Bayesian VAR (BVAR) merupakan salah satu penyelesaian terbaik untuk permasalahan tersebut (Koop & Korobilis, 2010).

Penelitian terkait metode BVAR antara lain, Kinasih (2009) menggunakan pendekatan metode BVAR untuk memodelkan konsumsi Provinsi Jawa Timur, dengan variabel yang digunaan adalah kredit konsumsi, pendapatan domestik regional bruto (PDRB), dan indeks harga konsumen (IHK). Dalam penelitian tersebut disimpulkan bahwa penggunaan prior informatif lebih meningkatkan akurasi peramalan. Sedangkan Antonio (2017), membandingkan faktor dinamis dan BVAR dalam memodelkan deret waktu multivariat untuk data makroekonomi. Hasil dari penelitian tersebut adalah model Bayesian VAR memberikan hasil peramalan yang akurat berdasarkan mean error (ME), root mean square error (RMSE), dan mean square error (MSE).

Indonesia khususnya Bali memiliki sektor pariwisata yang berkembang dengan pesat karena memiliki keindahan alam, keunikan budaya, dan keramahan masyarakat dalam menerima wisatawan. Pesatnya perkembangan pariwisata di Bali salah satunya ditunjukkan oleh angka jumlah kunjungan wisatawan mancanegara ke Bali. Data Badan Pusat Statistik Bali (BPS, 2019) menunjukkan angka jumlah kunjungan wisatawan mancanegara ke Bali pada tahun 2017 sebanyak 5.697.739 jiwa dan tahun 2018 bertambah sebesar 6,54 persen menjadi 6.070.473 jiwa. Peningkatan jumlah

kunjungan wisatawan mancanegara dipengaruhi oleh perkembangan jumlah kunjungan wisatawan Cina yang sangat pesat. Angka jumlah kunjungan wisatawan Cina ke Bali selalu meningkat tiap tahunnya sejak tahun 2014 hingga 2018, berturut-turut sejumlah 585.922, 688.489, 975.152, 1.356.412, dan 1.361.512. Jumlah ini cukup mengejutkan karena sebelumnya Australia adalah negara dengan jumlah kunjungan tertinggi. Namun pada tahun 2017 Cina berhasil menggeser kedudukan Australia sebagai negara yang memiliki jumlah kunjungan wisatawan tertinggi ke Bali.

Suwedayana (2016) memprediksi jumlah kunjungan wisatawan Australia ke Bali menggunakan metode time varying parameter (TVP). Dalam penelitian tersebut variabel penjelas yang digunakan adalah tingkat inflasi di Indonesia dan kurs AUD terhadap rupiah. Hasil penelitian menunjukkan bahwa nilai MAPE untuk penelitian tersebut sebesar 1,77 persen dan RMSPE yaitu 2,3418 persen. Sedangkan penelitian yang dilakukan oleh Suwartama (2017) mengenai peramalan jumlah kunjungan wisatawan Asia ke Bali menggunakan analisis regresi data panel dengan variabel bebas yaitu inflasi yang terjadi di Jepang dan Korea Selatan, serta kurs JPY, kurs KRW terhadap IDR. Hasil dari penelitian tersebut menunjukkan nilai mean absolute percentage error (MAPE) sebesar 17,5 persen dan 12,6 persen.

Berdasarkan uraian di atas, artikel ini ditujukan untuk memprediksi jumlah kunjungan wisatawan Cina ke Bali, nilai tukar mata uang Cina terhadap Rupiah, dan tingkat inflasi yang terjadi di Indonesia menggunakan metode Bayesian Vector Autoregression (BVAR).

• 2.    TINJAUAN PUSTAKA

• a. Vector Autoregressive (VAR)

Model VAR secara umum dapat ditulis sebagai berikut (Dieppe dkk. 2016):

yt =A i y_t- i + A ₂ yt- ₂ + - +A_p y_t -_p + ε_t (1) dengan y_t untuk t — 1,2,...,T adalah sebuah vektor data endogen berukuran n× 1, A₁,A₂,.,A_p merupakan p matriks koefisien variabel endogen berukuran ××n, dan ε_t adalah sebuah vektor galat berukuran × × 1. Pada persamaan (1) diasumsikan ε_t adalah peubah acak IID dengan nilai tengah 0 (nol)

dan varians Ʃ.

Persamaan (1) berlaku untuk setiap t, sehingga untuk perhitungan lebih lanjut model VAR dapat ditulis dalam bentuk transpose sebagai berikut:

dapat dilakukan dengan menggunakan aturan Bayes, yang menjadi dasar dari analisis Bayes.

Untuk parameter θ dan himpunan data y,

aturan Bayes dapat diperoleh dari definisi dasar

peluang bersyarat, dengan memperhatikan:

⎡ ∕₁ ⎤

^⎢ ∕₂ ^⎥

⎢^{⎢ ⋮} ⎥^⎥ ⎣⏟ ⎦

T×n

^{⎡ y}>                   r γ^{r ⎤}

⎢^{⎢⎢ y} _{⋮               ⋮}          ⋯ ^y _{⋮            ⋮} ⎥^⎥⎥

⎣⏟              ⋯             ⎦

T×k

π(θ|y)=

(e,y)₌ f(y|e)(e)

(y)=      (y)

(4)

Persamaan (4) mengungkapkan bahwa π(θ|y), distribusi posterior dari θ bergantung

^[ : _′⋮′^′ ; ^]

■'—v—'

(2)

T×n

dengan T merupakan ukuran sampel yang digunakan untuk setiap persamaan regresi dalam model VAR; n merupakan banyak variabel endogen yang digunakan; k merupakan banyak koefisien yang diestimasi untuk masing-masing persamaan dalam model VAR; dan ^cI merupakan banyak koefisien yang diestimasi untuk keseluruhan model VAR.

Persamaan (2) kemudian dapat ditulis

pada informasi yang terkandung dalam y , sama dengan produk dari data fungsi likelihood f(y|θ) dengan distribusi prior π(θ), dibagi dengan fungsi densitas f(y ) dari data. Karena penyebut f(y ) saling bebas terhadap θ , maka fungsi densitas f(y ) sering diabaikan. Maka persamaan (4) dapat ditulis kembali sebagai:

π(θ|y)∝f(y|θ)π(θ). (5)

Sering kali θ tidak akan menggambarkan satu parameter saja, melainkan menggambarkan beberapa parameter berbeda yang dipertimbangkan oleh model. Sehingga ini akan menunjukkan bahwa π(θ) menggambarkan distribusi prior bersama untuk semua parameter yang dipertimbangkan secara simultan, yang mana akan sulit untuk ditentukan.

dalam bentuk yang lebih sederhana sebagai berikut:

y=̅β+E.                 (3)

dengan

_ry_i ^,

y=   (Y)=

β=   (B)

yi,T

yn,1

, ̅=In ⨂X,

⎣    , ⎦

⎡⁽ _)⎤,

Cara sederhana yang dapat digunakan untuk mengatasi masalah ini adalah dengan mengasumsikan bahwa antarparameter tersebut saling bebas. Sehingga fungsi densitas bersama secara sederhana menjadi hasil kali dari fungsi densitas masing-masing parameter. Bentuk umum π(θ ) dengan d parameter dapat ditulis kembali sebagai:

π(θ)=π(01)×π(02)×…×π(0d). (6)

Misalkan, dalam model khas VAR yang terbentuk oleh dua parameter, ^l = dan ^2 =Ʃ, persamaan (6) dapat ditulis kembali:

π(0|y)∝f(y|0)π(β)π(Ʃ). (7)

b. Estimasi Bayesian VAR

Dieppe dkk. (2016) mengungkapkan bahwa prinsip dari analisis Bayesian adalah untuk menggabungkan informasi awal yang mungkin dimiliki tentang distribusi untuk sebuah parameter (distribusi prior) dengan informasi yang terkandung dalam data (fungsi likelihood) untuk memperoleh perhitungan distribusi untuk kedua informasi tersebut, yang diketahui sebagai distribusi posterior. Hal ini

c. Distribusi Prior

Menurut Box dan Tiao (1973) biasanya keputusan penentuan distribusi prior memegang peranan penting dalam satu analisis Bayes. Analisis Bayes mengombinasikan informasi awal dalam distribusi prior dan informasi sampel dalam fungsi kemungkinan (likelihood) untuk selanjutnya membentuk distribusi posterior. Agrippino & Ricco (2018) mengatakan bahwa salah satu prior yang biasa digunakan untuk variabel-variabel ekonomi adalah Normal-Wishart prior.

Dalam distribusi Normal-Wishart Prior diasumsikan bahwa kedua parameter β dan Ʃ tidak diketahui (Dieppe dkk., 2016). Diberikan

fungsi densitas peluang yaitu:

f(y|β,Ʃ)∝|Ʃ̅| ² exp 0- I(β - ^̂) (Ʃ⨂(Х' Х)-¹)-¹(β-̂)1×

|Ʃ| ^[(T-k-n-1 ⁾ +n+1]/ ² exp 0- 2^fr2Ʃ-¹(Y-

x ̂) (Y^-X̂)31.                      (8)

dengan

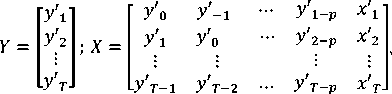
^̂ dan ^̂ merupakan sebuah estimasi OLS parameter B dan β.

Persamaan (8) dapat dikenali sebagai kernel dari sebuah distribusi normal multivariat

(untuk β) dan kernel dari sebuah distribusi inverse Wishart (untuk Ʃ), keduanya berpusat di sekitar penduga OLS.

Dengan demikian, diasumsikan distribusi normal multivariat untuk prior :

β^~ JV- (β₀,Ʃ⨂Φo)                (9)

dengan βo adalah vektor Q×1, Φθ adalah matriks diagonal k×k , dan Ʃ adalah matriks residual varians-kovarian, yang berarti Ʃ⨂ΦQ adalah matriks kovarian nk × nk atau Q×Q.

Prior untuk β dapat ditulis sebagai:

π(β)∝|Σ| ²

exp 0-(-₂)(β- β₀ ⁾ ' (Σ⨂ φ₀ )^¹⁽β- β₀)1.   (10)

Sedangkan, distribusi prior untuk Ʃ adalah distribusi inverse Wishart yang digambarkan sebagai:

Σ ~ℐW(S₀ , a₀).               (11)

dengan 5₀ adalah matriks skala n×n untuk prior dan a₀ adalah derajat kebebasan prior pada persamaan (11).

Prior untuk Ʃ dapat ditulis sebagai: a₀+τι+l Γ 1

π(Σ)∝|Σ|   2 exp 0-~tr{^⅛0}1.

Jadi, diperoleh distribusi posterior yaitu: π(β, Ʃ|y) ∝|Ʃ| ²exp0-(f)(β- ^̅)(Ʃ⨂Φ̅) ^¹(β-

̅+n+l      Γ 1- 1

̅)1×|Ʃ|   ² exp0-2^fr{Ʃ   ̅}1.(13)

dengan

Φ^̅=[Φ^̅o¹ +X′X] -^ ,

̅=vec( ^̅), ^̅=Φ^̅[Φ^̅O¹B₀ +X′Y],

̅=T+ «o ,

̅= Y'Y + S₀ +B′oΦO¹Bo - ^̅′Φ^̅ -¹ ̅.

• d.    Markov Chain Monte Carlo (MCMC)

Metode MCMC sangat erat hubungannya dengan metode Bayes. Pada beberapa kasus bentuk distribusi posterior biasanya rumit dan sulit diintegralkan, sehingga distribusi marginal posterior juga sulit untuk diintegralkan. Salah satu solusi alternatif adalah menggunakan

metode simulasi MCMC. Salah satu algoritme dari MCMC adalah Gibbs Sampler.

• e.    Gibbs Sampling

Gibbs sampler adalah teknik untuk membangkitkan variabel acak dari sebuah distribusi (marginal) secara tidak langsung, tanpa harus menghitung densitas.

• f.    Impulse Response Function (IRF)

Karena koefisien individual pada model VAR yang diestimasi terkadang sulit untuk diinterpretasikan, biasanya pengguna VAR sering kali mengestimasi dengan suatu cara yang disebut impulse response function (IRF) (Gujarati, 2004). IRF berguna untuk melihat interaksi secara kasar antarvariabel respons pada model VAR. Fungsi respon impuls yang digambarkan dalam bentuk grafik dapat digunakan untuk mengetahui perilaku setiap variabel atas perubahan yang terjadi pada variabel lain dalam sistem.

• g.    Kriteria Nilai MAPE

Kemampuan model dalam melakukan peramalan bisa dilihat dari hasil perhitungan ketepatan peramalan. Mean abosolute percentage error (MAPE) merupakan salah satu statistik yang dapat digunakan untuk mengukur ketepatan ramalan. Nilai MAPE dirumuskan sebagai (Lu □ tkepohl and Kratzig, 2004):

MAPE = ∑Γ=ι ^| y_c ̅ ^t-^|×100%        (14)

dengan n merupakan banyak data, y□t merupakan hasil peramalan, dan yt merupakan nilai yang sesungguhnya dari variabel yang diprediksi. Kriteria peramalan MAPE dapat dilihat lebih rinci pada Zhang T. dkk, 2015.

• 3. METODE PENELITIAN

Data yang digunakan dalam penelitian ini yaitu data jumlah kunjungan wisatawan Cina ke Bali yang diperoleh dari Dinas Pariwisata Provinsi Bali (JMW) pada situs https://disparda.baliprov.go.id, inflasi yang terjadi di Indonesia (INF), dan kurs CNY terhadap IDR (KURS) yang diperoleh dari Bank Sentral Republik Indonesia (BI) pada situs https://www.bi.go.id. Data yang digunakan adalah data bulanan periode Januari 2010--Juni 2019. Data bulan Januari 2010--Desember 2018 digunakan untuk pembentukan model, sedangkan data bulan Januari 2019--Juni 2019 digunakan untuk menghitung nilai MAPE.

Langkah-langkah pengolahan data yang dilakukan dalam penelitian ini adalah sebagai berikut:

• a.    Memilih prior untuk masing-masing parameter VAR, yaitu distribusi NormalWishart Prior.

• b.    Menganalisis distribusi posterior.

• c.    Menentukan nilai estimasi parameter menggunakan metode MCMC dengan menggunakan algoritma Gibbs Sampler.

• d.  Melakukan analisis  keakuratan hasil

peramalan dengan menghitung MAPE.

• e.  Melakukan peramalan JMW, INF, dan

KURS dalam periode bulan Juli 2019 hingga Maret 2020.

• f.   Analisis fungsi respon impuls.

• g.  Menginterpretasi hasil yang diperoleh.

Secara sederhana bentuk dapat ditulis kembali seperti dengan

rYι,11

y=   (Y)=

β=   (B)=

4. HASIL DAN PEMBAHASAN

a. Model Vector Autoregression (VAR)

Salah satu kesulitan terbesar dalam

pembentukan model VAR adalah penentuan

panjang lag yang tepat (Gujarati, 2004). Pemilihan lag dalam penelitian ini berdasarkan pada studi empiris pada jurnal Ivanov & Kilian (2005) dan percobaan pada beberapa model VAR dengan panjang lag berbeda. Pada penelitian ini menggunakan 3 variabel endogen dan banyak sampel tiap persamaan sebanyak 12 dengan mempertimbangkan banyak data bulanan yang digunakan dalam setahun, serta

dengan panjang lag 4 maka diperoleh model

VAR sebagai berikut:

⎡    ^, _⎤

^⎢ Yi ⋮_, 12 ^⎥

⎢ y₂ ^,

^⋮

⎢ y₂ ^,12

⎢ y₃ ,

⎢^⎢         ⋮^,       ⎥^⎥

⎣    ,   ⎦

×

0⋯

'4ι ^{( )}

λ₄⁽¹⁾

41 ⁽²⁾

+

persamaan (14) persamaan (3),

4₄⁽²⁾

4ι ⁽³⁾

⎣    ⁽ )_⎦

0

_⎡ ^, _⎤

⎢ ≡ι ,12 ⎥

⎢^{⎢ ε} ⋮^,, ⎥^⎥

⎢    ^,12 ⎥

⎢^{⎢ ε} _⋮,_, ⎥^⎥

⎣   ,   ⎦

⁰

⋮

0⎥

/-₃ ⎥

_⋮⎥

⎦

(14)

Yi,12 y₂ ,1

Y₂ ,12 y₃ ,1

⎥, ̅=I∏ ⨂x,

⎣    ,   ⎦

⎡^{( 1} )_⎤ ⎢⋮⎥ ^{⎢a( )}⎥^⎥ ⎢⋮⎥ ⎢                  ⎥^,

_⎢⎢^⎢ ‘ ⁽_⋮ ⁾⎥^⎥

Δ^{( )}

LZi₄

Γ ^εl ,1

^,

^εl,12

(15)

ε=   (ℰ)=

(16)

E₃ ,1

⎣   ,   ⎦

b. Memilih Prior dan Menentukan

Posterior

Agrippino & Ricco (2018) mengatakan bahwa salah satu prior yang biasa digunakan untuk variabel-variabel ekonomi adalah Normal-Wishart prior. Dalam model VAR pada penelitian ini, parameter yang digunakan adalah β yang merupakan sebuah vektor dari gabungan koefisien model VAR seperti dapat dilihat pada persamaan (16) dan Ʃ yang merupakan matriks kovarian dari galat pada persamaan (16).

Pemilihan prior untuk masing-masing parameter dapat diawali dengan memperhatikan fungsi densitas peluang seperti pada persamaan (8). Fungsi densitas peluang untuk penelitian ini menggunakan n=3 danT=12, sehingga diperoleh fungsi densitas peluang yang dinyatakan pada persamaan (17):

⟺f(y|β,Ʃ)=(2π) ( )( ) |Ʃ̅| ² exp 0- I(y-

̅β⁾ ' Ʃ̅-¹(y- ^̅β)1.

⟺f(y|β,Ʃ)=(2π) ² |Ʃ̅| ² exp 0- I(y-

̅β⁾ ' Ʃ̅ (y- ^̅β)1.

⟺f(y|β,Ʃ)=(2π) -18 |Ʃ̅| ² exp 0- I(y-

̅β⁾ ' Ʃ̅-¹(y- ^̅β)1.               (17)

Selanjutnya, dengan memperhatikan nilai k=12, maka prior untuk parameterβ dalam penelitian ini dinyatakan pada persamaan (18):

π(β)∝|Ʃ| ² exp0-(I)(β- β₀ )' (Ʃ⨂ΦO)-¹(β- β₀)1 (18) dan prior untuk parameter Ʃ dinyatakan pada persamaan (19):

ap+3+ι Γ 1         .1

⟺π(Ʃ) ∝|Ʃ|   2 exp 0-~tr{Ʃ ¹¾ }1

CCq+4 Γ 11

⟺π(Ʃ) ∝|Ʃ|  2 exp 0- 2^tr {Ʃ~¹S₀}1.

Berdasarkan prior yang telah dipilih maka diperoleh posterior yang dinyatakan pada persamaan (20):

π(β, Ʃ|y) ∝|Ʃ| ² exp0-.I/(β - ^̅) (Ʃ⨂Φ̅)-¹(β-

̅)1×|Ʃ|  ² exp0-2^tr{Ʃ-¹ ̅}1.     (20)

• c.    Menentukan Nilai Estimasi Parameter

Untuk menentukan nilai estimasi parameter dari distribusi posterior yang berbentuk seperti persamaan (20) digunakan algoritma Gibbs Sampling seperti yang tertulis pada subbagian 2e. dengan bantuan toolbox Bayesian Estimation, Analysis and Regression (BEAR) pada Matlab 2017a.

• d.    Menghitung Ketepatan Peramalan

Ketepatan peramalan dapat ditunjukkan oleh nilai MAPE yang diukur menggunakan persamaan (14). Data aktual yang digunakan adalah data JMW, INF, dan KURS pada bulan Januari 2019 sampai Juni 2019, sedangkan data hasil peramalan diperoleh dari analisis distribusi posterior pada persamaan (20). Perhitungan nilai MAPE selengkapnya ditunjukkan pada Tabel 1.

Tabel 1. Nilai MAPE Peramalan Jumlah Kunjungan Wisatawan Cina ke Bali

Waktu (2019)	Jumlah Kunjungan Wisatawan (yu)	Peramalan Jumlah Kunjungan Wisatawan (̅It)	| ⅛ -̅It | yit
Januari	115.491	86.610,37	0,25
Februari	122.643	91.395,09	0,25
Maret	89.178	93.253,76	0,05■
April	94.202	96.424,74	0,02
Mei	93.514	97.427,78	0,04■
Juni	103.955	98.564,49	0,05
	Total		0,67
0, 67 MAPE=,  ×100%=11, 13 % 6

peramalan baik dan peramalan sangat akurat dengan nilai sebesar 17,93 persen dan 0,81 persen. Proses perhitungan kedua nilai MAPE tersebut menggunakan perhitungan nilai MAPE seperti perhitungan nilai MAPE peramalan JMW.

• e.    Peramalan dengan Bayesian Vector Autoregression

Berikut hasil dan plot peramalan data JMW, INF, KURS pada periode bulan Juli 2019 sampai Maret 2020.

Tabel 2. Peramalan jumlah kunjungan wisatawan Cina ke Bali, inflasi yang terjadi di Indonesia, dan kurs CNY terhadap IDR pada Juli 2019--Maret 2020

Berdasarkan Tabel 1. peramalan JMW termasuk baik, karena nilai MAPE yang diperoleh sebesar 11,13 persen.

Nilai MAPE peramalan INF dan peramalan KURS berturut-turut merupakan

Bulan	Jumlah Kunjungan Wisatawan	Inflasi	Kurs
Juli 2019	99.137,16	3,52	2.075,97
Agustus 2019	97.638,12	3,65	2.075,62
September 2019	96.133,93	3,63	2.070,44
Oktober 2019	96.356,97	3,64	2.071,82
November 2019	94.970,50	3,73	2.071,59
Desember 2019	96.788,30	3,82	2.070,66
Januari 2020	96.736,97	3,76	2.072,73
Februari 2020	96.276,44	3,79	2.069,16
Maret 2020	96.140,81	3,79	2.073.51

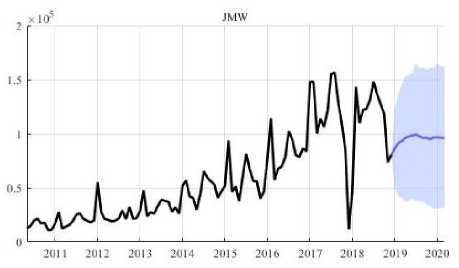
Gambar 1.Plot Data Aktual dan Peramalan Jumlah Kunjungan Wisatawan Cina ke Bali

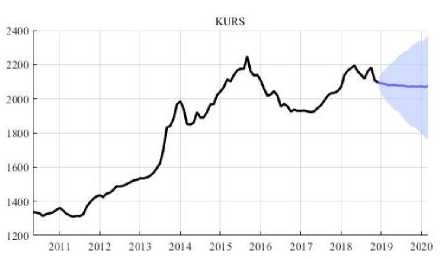
Gambar 3.Plot Data Aktual dan Peramalan Kurs CNY terhadap IDR

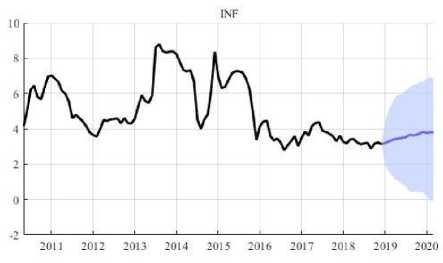
Gambar 2.Plot Data Aktual dan Peramalan Inflasi yang Terjadi di Indonesia

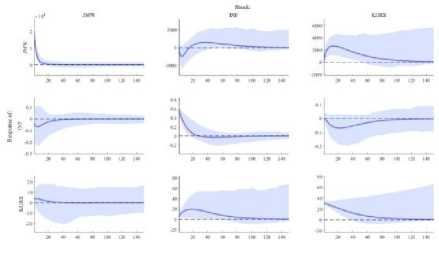
Gambar 4.Plot IRF Jumlah Kunjungan Wisatawan Cina ke Bali, Inflasi yang Terjadi di Indonesia, dan Kurs CNY terhadap IDR

Berdasarkan Gambar 1. terlihat bahwa data JMW pada bulan Januari 2010--Juni 2019 menunjukkan pola data tren musiman. Gambar 2. menunjukkan bahwa data INF memiliki pola cenderung konstan, terutama sejak periode Januari 2016 hingga Juni 2019, dan Gambar 3. memperlihatkan bahwa data KURS pada bulan Januari 2010--Juni 2019 memiliki pola tren naik.

• f.    Impulse Response Function (IRF)

Fungsi respon impuls yang digambarkan dalam bentuk grafik dapat digunakan untuk mengetahui perilaku setiap variabel atas perubahan yang terjadi pada variabel lain dalam sistem. Berikut plot IRF dari JMW, INF, dan KURS.

Gambar 4. menunjukkan plot IRF dari ketiga variabel endogen model BVAR yang ditampilkan secara bersamaan sehingga dapat dilihat hubungan dinamis antara masing-masing variabel endogen dari model BVAR pada penelitian ini. Pembahasan lebih lanjut tentang masing-masing plot IRF pada Gambar 4. akan dijelaskan dengan Gambar 5. sampai Gambar 10.

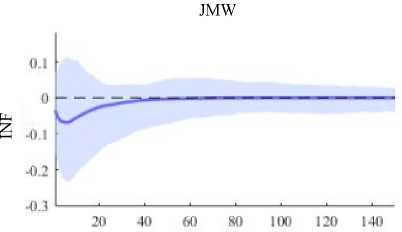
Gambar 5. Plot IRF Jumlah Kunjungan Wisatawan Cina ke Bali terhadap Inflasi yang Terjadi di Indonesia

Gambar 5. memperlihatkan adanya reaksi negatif terhadap jumlah kunjungan wisatawan Cina ke Bali setelah bulan pertama sampai bulan ke-15 karena adanya shock dari inflasi yang terjadi di Indonesia. Setelah bulan ke-15 jumlah kunjungan wisatawan Cina ke Bali menunjukkan reaksi positif dan kemudian setelah bulan ke-120 cenderung stabil.

Gambar 6. Plot IRF Jumlah Kunjungan Wisatawan Cina ke Bali terhadap Kurs CNY terhadap IDR

Pada Gambar 6. terlihat adanya reaksi positif terhadap jumlah kunjungan wisatawan Cina ke Bali setelah bulan pertama sampai bulan ke-120 karena adanya shock dari kurs CNY terhadap IDR dan kemudian stabil.

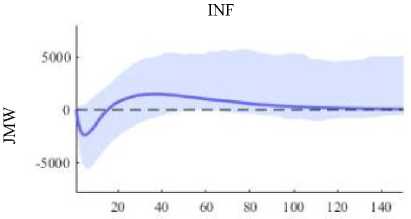
Gambar 7. Plot IRF Inflasi yang Terjadi di Indonesia     terhadap     Jumlah

Kunjungan Wisatawan Cina ke Bali

Gambar 7. menunjukkan adanya reaksi negatif terhadap inflasi yang terjadi di Indonesia setelah bulan pertama sampai bulan ke-40 karena adanya shock dari jumlah kunjungan wisatawan Cina ke Bali. Setelah bulan ke-40 reaksi dari inflasi yang terjadi di Indonesia cenderung stabil.

Dapat dilihat pada Gambar 8. bahwa shock dari kurs CNY terhadap IDR menyebabkan adanya reaksi negatif terhadap inflasi yang terjadi di Indonesia setelah bulan pertama sampai bulan ke-120. Setelah bulan ke-120 inflasi yang terjadi di Indonesia cenderung stabil.

JMW

20

10

20

20    40    60 SO IOO 120   140

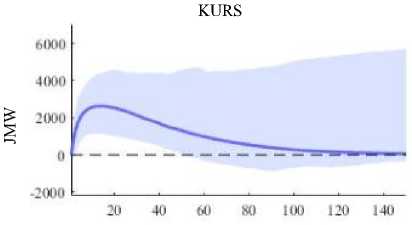
Gambar 9.Plot IRF Kurs CNY terhadap IDR terhadap    Jumlah    Kunjungan

Wisatawan Cina ke Bali

Pada Gambar 9. terlihat bahwa setelah bulan pertama sampai bulan ke-30 terdapat reaksi positif pada kurs CNY terhadap IDR karena adanya shock dari jumlah kunjungan wisatawan Cina ke Bali. Setelah bulan ke-30 kurs CNY terhadap IDR cenderung stabil.

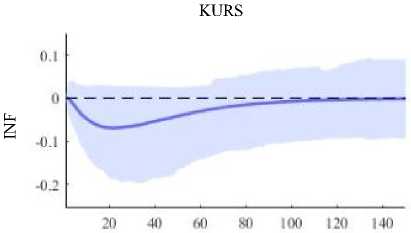
Gambar 8. Plot IRF Inflasi yang Terjadi di Indonesia terhadap Kurs CNY terhadap IDR

Pada Gambar 10. terlihat adanya reaksi positif terhadap kurs CNY terhadap IDR setelah bulan pertama sampai bulan ke-100 karena adanya shock dari inflasi yang terjadi di Indonesia. Setelah bulan ke-100 reaksi shock dari inflasi yang terjadi di Indonesia pada kurs CNY terhadap IDR cenderung stabil.

• 5.    KESIMPULAN DAN SARAN

• a. Kesimpulan

Nilai MAPE untuk jumlah kunjungan wisatawan Cina ke Bali dan inflasi yang terjadi di Indonesia menunjukkan peramalan baik yaitu secara berturut-turut sebesar 11,13 persen

INF

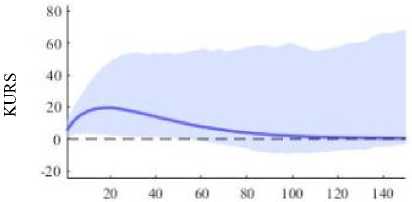
Gambar 10. Plot IRF Kurs CNY terhadap IDR terhadap Jumlah Kunjungan Wisatawan Cina ke Bali

dan 17,93 persen, sedangkan nilai MAPE untuk kurs CNY terhadap IDR diperoleh sebesar 0,81 persen yang menunjukkan peramalan sangat akurat.

Hasil peramalan yang diperoleh untuk jumlah kunjungan wisatawan Cina ke Bali, inflasi yang terjadi di Indonesia, dan kurs CNY terhadap IDR pada periode bulan Juli 2019 sampai Maret 2020 menunjukkan angka-angka yang cenderung stabil. Adapun rata-rata jumlah kunjungan wisatawan Cina ke Bali, inflasi yang terjadi di Indonesia, dan kurs CNY terhadap IDR perbulan secara berurutan sebesar 96.686 orang; 3,71 persen; dan Rp2.072.

b. Saran

Saran yang dapat diberikan untuk penelitian selanjutnya yaitu diharapkan dapat mencoba menambahkan prior selain NormalWishart, dapat menambahkan variabel endogen lainnya seperti jarak tempuh dari negara asal menuju negara destinasi, musim di negara asal, dan kemenarikan destinasi pesaing, ataupun menambahkan variabel eksogen sehingga dapat mencoba analisis BVAR eksogenus.

DAFTAR PUSTAKA

Agrippino, S. M. & Ricco, G. 2018. Bayesian

Vector Autoregressions. Staff Working Paper, No. 756. Bank of England.

Antonio, Y., Warsono & Kurniasari, D. 2017. Kemampuan Faktor Dinamis dan Bayesian VAR (BVAR) pada Pemodelan Multivariate Time-Series untuk Data Makroekonomi.

Skripsi. Bandar Lampung:   Jurusan

Matematika FMIPA UNILA.

Box, G. E. P. & Tiao, G. 1973. Bayesian Inference in Statistical Analysis. Addison-Wesley Publishing Company.

Casella, G. & George, E.I. 1992. Explaining the Gibbs  Sampler.   American Statistical

Association.

Dieppe, A., Legrand, R. & B. v. Roye. 2016. The BEAR toolbox. in Working Paper Series. European Central Bank (ECB).

Gujarati, D. N. 2004. Basic Econometrics. 4th ed. New York: McGraw-Hill.

Heizer, J., Render, B. & Munson, C. 2011. Operations Management Sustainability and Supply Chain Management. Boston: Pearson.

Ivanov, V. & Kilian, L. 2005. A Practitioner’s Guide to Lag Order Se lection for VAR Impulse Response Analysis. Studies in Nonlinear Dynamics & Econometrics, Vol.

9, No.1, Article 2. The Berkeley Electronic Press.

Kinasih, I. P., Soehardjoepri & Agustini, F. W. 2009. Pendekatan Metode Bayesian Vector Autoregresif (BVAR) untuk Model Konsumsi wilayah Jawa Timur. Skripsi. Surabaya: Jurusan Matematika FMIPA ITS.

Koop, G. & Korobilis, D. 2010. Bayesian Multivariate Time Series Methods for Empirical Macroeconomics. Foundations and Trends in Econometrics, Vol. 3, No. 4, pp. 267-358.

Lütkepohl H. & Krätzig M. 2004. Applied Time Series Econometrics. New York: Cambridge University Press.

Sumara, R. & Kusdarwati, H. 2017. Model Bayesian Vector Autoregressive (BVAR) (Studi Kasus Analisis Hubungan Antara Pertumbuhan Ekonomi dan Ekspor Indonesia). Skripsi. Malang: Program Studi Statistika, Jurusan Matematika, FMIPA, Universitas Brawijaya.

Suwartama, K. H. 2017. Aplikasi Analisis Regresi Data Panel dalam Meramalkan Jumlah Kunjungan Wisatawan Asia ke Bali. Skripsi. Denpasar:    Jurusan

Matematika, FMIPA, Universitas Udayana

Suwedayana, I P. G. D. G. 2016. Peramalan Jumlah Kunjungan Wisatawan Australia yang Berkunjung ke Bali Menggunakan Model Time Varying Parameter (TVP). Skripsi. Denpasar: Jurusan Matematika, FMIPA, Universitas Udayana

Zhang, T. , Wang, K. & Zhang, X. 2015. Modelling and Analyzing the Transmission Dynamics of HBV Epidemic in Xinjiang, China. Journal PLOS One. Vol. 10, No. 9, pp. 1-14.

94