MEMODELKAN ANGKA GIZI BURUK DI PROVINSI BALI DENGAN PENDEKATAN REGRESI SPASIAL
on
E-Jurnal Matematika Vol. 10(2), Mei 2021, pp. 103-110
DOI: https://doi.org/10.24843/MTK.2021.v10.i02.p328
ISSN: 2303-1751
MEMODELKAN ANGKA GIZI BURUK DI PROVINSI BALI DENGAN PENDEKATAN REGRESI SPASIAL
Anak Agung Istri Ayu Pratami1§, I Komang Gde Sukarsa2, Ni Luh Putu Suciptawati3, Eka N Kencana4
1Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email : gekkistri@gmail.com]
2Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email : gedesukarsa@unud.ac.id]
3Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email : suciptawati@unud.ac.id]
4Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email : i.putu.enk@unud.ac.id]
§Corresponding Author
ABSTRACT
Nutritional problems in toddler are still a serious problem in various districts/cities in Indonesia. The case of malnutrition in Bali Province vary in many regions and hypothesized to be influenced by geographic location, which is often known as spatial heterogeneity. To overcome this problem, a spatial regression method is used on this research. This study aims to model the factors that are hypothesized affect malnourished toddlers in Bali Province using spatial regression methods, i.e. spatial autoregressive model (SAR) and spatial error model (SEM). Both models have 5 predictors variable, i.e. the percentage of toddlers aged between 6 - 59 months who received vitamin A, the percentage of babies with low birth weight (LBW), the percentage of households with clean and healthy living behavior (PHBS), the percentage of children under five receiving exclusive breastfeeding, and the percentage of toddler health services, which are obtained from Bali Provincial Health Office. The results showed SEM method produced smaller AIC value and higher R2, with R2 and AIC values of 96.24% and 60.84, respectively.
Keywords: Malnourished Toddler, Spatial Effect, SEM, SAR
Salah satu permasalahan yang dihadapi terkait status gizi yaitu gizi buruk. Gizi buruk merupakan suatu kondisi kurangnya nutrisi pada tubuh atau nutrisinya di bawah standar. Gizi buruk dapat menimpa semua kelompok umur di masyarakat, tetapi yang perlu diperhatikan adalah kelompok bayi dan balita. Hal tersebut karena usia ini merupakan masa tumbuh kembang yang optimal (golden period) sehingga apabila terjadi gangguan pada usia ini, tidak dapat dicukupi pada masa berikutnya dan dapat berpengaruh negatif pada kualitas generasi penerus (Profil Kesehatan Provinsi Bali, 2019).
Masalah gizi pada kelompok balita masih menjadi masalah serius di berbagai kabupaten/kota di Indonesia. Kekurangan gizi pada balita dapat menyebabkan penurunan tingkat kecerdasan pada anak. Hal tersebut menyebabkan menurunnya kualitas sumber daya manusia, yang berakibat berkurangnya potensi kalangan muda yang sangat dibutuhkan dalam pembangunan bangsa.
Berdasarkan data yang diperoleh dari Dinas Kesehatan Provinsi Bali, kasus gizi buruk pada balita di Bali tahun 2018 sebanyak 111 kasus, mengalami peningkatan dari tahun sebelumnya, sebanyak 106 kasus.
Provinsi Bali memiliki 9 kabupaten yang secara geografis memiliki karakteristik yang berbeda, sehingga peneliti menduga ada kemungkinan bahwa kasus balita gizi buruk di Provinsi Bali dipengaruhi oleh letak geografis atau lokasi pengamatan karena kondisi wilayah satu tidak sama dengan kondisi wilayah lainnya. Mencermati hal ini, model angka gizi buruk pada balita di Provinsi Bali dibuat dengan menggunakan metode regresi spasial yang merupakan pengembangan dari metode analisis regresi linier, di mana aspek lokasi juga diperhatikan.
Berdasarkan kelinearan data, model regresi dikelompokkan menjadi dua, yaitu regresi linear dan nonlinear. Apabila aspek keruangan juga diperhatikan, maka model regresi yang digunakan adalah regresi spasial. Pemodelan spasial dapat dibedakan menjadi pemodelan dengan pendekatan titik yang meliputi
Geographically Weighted Regression (GWR), Geographically Weighted Poisson Regression (GWPR), dan Generalized Space-Time Autoregressvie (GSTAR) dan pemodelan dengan pendekatan area yang meliputi Spatial Autoregressive Model (SAR), Spatial Error Model (SEM), Spatial Durbin Model (SDM), Spatial Autoregressive Moving Average (SARMA), dan panel data.
SAR adalah model regresi spasial yang mengasumsikan variabel terikat pada suatu wilayah dipengaruhi oleh variabel terikat di wilayah lainnya dalam model (terdapat korelasi spasial pada variabel terikat). Sedangkan SEM mengasumsikan bahwa pada error model suatu wilayah dengan wilayah lainnya terdapat korelasi spasial (LeSage & Pace, 2009).
Metode regresi spasial pernah digunakan oleh Jayanti, et al. (2017) untuk memodelkan kasus Demam Berdarah Dengue (DBD) di Kota Denpasar. Hasil penelitian tersebut menunjukkan bahwa variabel yang berpengaruh signifikan terhadap DBD adalah faktor ketetanggan antardaerah, persentase luas wilayah, dan persentase peran jumantik pada setiap desa/kelurahan, serta nilai R2 pada model SAR sebesar 54,9% dan AIC sebesar 166,35.
Model persamaan regresi berganda secara umum dapat dituliskan sebagai berikut (Draper & Smith, 1998):
Yi=βo+ βι%ιi+⋯+βk%ki + Zi (1)
dengan : Yi merupakan nilai pengamatan variabel terikat; βQ,β ,β2,…,βk merupakan koefisien regresi; X1,X2,…,Xk merupakan nilai pengamatan variabel bebas; εi merupakan nilai galat/error regresi dengan asumsi εi ~IIND (0, σ2); i=1,2,3,…,n.
Matriks pembobot spasial merupakan matriks yang menggambarkan kedekatan hubungan antar lokasi. Bentuk umum dari matriks pembobot spasial yaitu :
Matriks tersebut akan distandarisasi dengan rumus (LeSage & Pace, 2009):
∗ wij'
dimana W merupakan matriks pembobot spasial, wij merupakan elemen baris ke – i kolom ke - j matriks pembobot spasial.
Menurut LeSage & Pace (2009), matriks pembobot spasial tipe area terdiri dari rook
contiguity, double rook contiguity, linear contiguity, double linear contiguity, bishop contiguity, dan queen contiguity. Matriks pembobot yang digunakan dalam penelitian ini adalah queen contiguity.
Regresi spasial merupakan salah satu metode statistika yang digunakan untuk mengetahui hubungan antara variabel dependen dan variabel independen dengan
mempertimbangkan ketergantungan spasial. Secara umum, model persamaan regresi spasial dinyatakan sebagai berikut (Anselin, et al., 2004):
y= + xβ +U (3)
U= +ε
ε~N (0, σ2I)
Spatial Autoregressive Model (SAR) disebut juga dengan Spatial Lag Model (SLM) (Anselin, et al., 2004). Apabila nilai p≠ 0 dan λ=0, maka model tersebut merupakan model SAR. Adapun model persamaannya yaitu:
y= + xβ +ε (4)
dimana y adalah variabel respon, x adalah matriks variabel penjelas, W adalah matriks pembobot spasial, ε merupakan vektor error dengan varian konstan σ2 ,β adalah vektor koefisien parameter regresi, p adalah koefisien autoregresi lag spasial, dan A merupakan koefisien autoregresi galat spasial.
Apabila nilai p=0dan A≠0, maka model tersebut merupakan model SEM. model regresi spasialnya menjadi :
y= +U (5)
U= +ε
ε=(I- AW)(y- xβ )
Tujuan dari penelitian ini yaitu untuk mengetahui model regresi spasial dan factor – factor yang memengaruhi angka gizi buruk pada balita di Provinsi Bali.
Data yang digunakan yaitu data sekunder yang diperoleh dari Dinas Kesehatan Provinsi Bali. Unit pengamatan yang digunakan adalah seluruh kabupaten/kota yang ada di provinsi Bali.
Penelitian ini menggunakan dua jenis variabel yaitu variabel respon dan variabel prediktor. Variabel respon yang digunakan
yaitu jumlah kasus gizi buruk pada balita sedangkan variabel prediktor yang digunakan yaitu persentase balita usia 6 – 59 bulan yang mendapat vitamin A (X1 ), persentase bayi dengan Berat Badan Lahir Rendah (BBLR) (X2 ), persentase rumah tangga ber-PHBS (X3 ), persentase balita mendapatkan ASI eksklusif (X4), dan persentase pelayanan kesehatan balita (X5).
Teknik analisis yang digunakan pada penelitian ini setelah melalui proses pengumpulan data yaitu sebagai berikut.
-
1. Membentuk peta tematik untuk melihat penyebaran masing – masing variabel
-
2. Melakukan Uji Moran’s I untuk masing – masing variabel
-
3. Melakukan Uji Lagrange Multiplier (LM)
-
4. Membentuk Matriks Pembobot Spasial
-
5. Melakukan pemodelan Spatial
Autoregressive Model (SAR) dan Spatial Error Model (SEM)
-
6. Membandingkan model SAR dan SEM dengan melakukan pemilihan model terbaik menggunakan nilai AIC minimum dan atau R2 terbesar.
-
7. Melakukan interpretasi model terbaik yang diperoleh
Berikut ini merupakan penyebaran dari setiap variabel yang digambarkan melalui peta tematik.
3.1.1 Jumlah Kasus Balita Gizi Buruk di Provinsi Bali
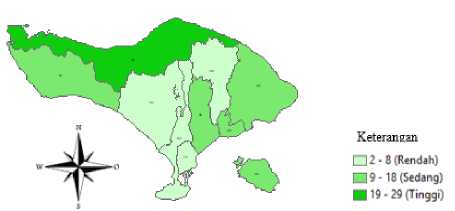
Gambar 1. Peta Penyebaran Kasus Balita Gizi Buruk di Provinsi Bali Tahun 2018
Jumlah kasus terbanyak yaitu sebesar 29 kasus yang terjadi pada kabupaten Buleleng, sedangkan kasus terendah sebanyak 2 kasus yaitu pada kota Denpasar. Warna yang semakin
gelap pada peta tematik mengindikasikan jumlah kasus balita gizi buruk yang semakin banyak. Sebaliknya, warna yang semakin terang mengindikasikan jumlah kasus balita gizi buruk yang semakin sedikit.
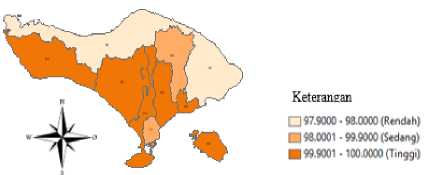
Gambar 2 Persentase Balita Usia 6 – 59 Bulan yang Mendapat Vitamin A di Provinsi Bali Tahun 2018
Warna yang semakin gelap
mengindikasikan persentase balita usia 6 – 59 bulan yang mendapat vitamin A yang semakin banyak, sedangkan warna yang semakin terang mengindikasikan persentase balita usia 6 – 59 bulan yang mendapat vitamin A yang semakin rendah. persentase balita usia 6 – 59 bulan yang mendapat vitamin A tertinggi sebesar 100 persen yaitu pada kabupaten Jembrana, Tabanan, Badung, Klungkung dan persentase balita usia 6 – 59 bulan yang mendapat vitamin A terendah sebesar 97,90 persen pada Kabupaten Karangasem.
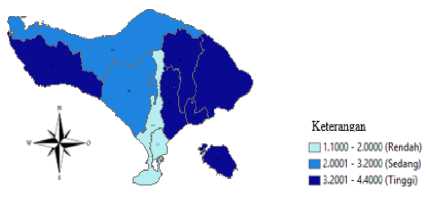
Gambar 3 Persentase Bayi dengan Berat Badan Lahir Rendah (BBLR) di Provinsi Bali Tahun 2018
Warna yang semakin gelap mengindikasikan bahwa persentase bayi dengan Berat Badan Lahir Rendah (BBLR) semakin tinggi dan warna yang semakin terang mengindikasikan bahwa persentase bayi dengan Berat Badan Lahir Rendah (BBLR) semakin
rendah. Persentase yang tertinggi yaitu sebesar 4,4 persen pada Kabupaten Klungkung, sedangkan persentase terendah yaitu sebesar 1,1 persen kasus pada Kota Denpasar. Kabupaten Badung dan Denpasar memiliki persentase kasus BBLR yang rendah. Hal ini berarti, secara kinerja, Kabupaten Badung dan Denpasar telah mampu untuk menghindari BBLR.
3.1.4 Persentase Rumah Tangga Ber-PHBS
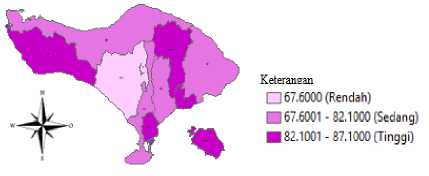
Gambar 4. Persentase Rumah Tangga Ber – PHBS di provinsi Bali Tahun 2018
Warna yang semakin gelap mengindikasikan bahwa persentase rumah tangga ber – PHBS semakin tinggi, sedangkan warna yang semakin terang mengindikasikan persentase rumah tangga ber – PHBS yang semakin rendah. Persentase rumah tangga ber – PHBS di Provinsi Bali tahun 2018 tertinggi yaitu sebesar 87,1 persen pada Kabupaten Klungkung dan terendah sebesar 67,6 persen pada Kabupaten Tabanan.
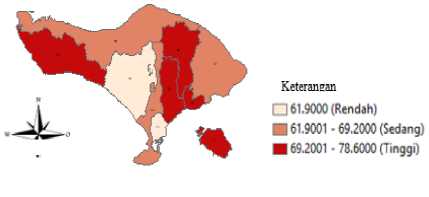
Gambar 5 Persentase Balita Mendapat ASI Eksklusif di Provinsi Bali tahun 2018
Warna yang semakin gelap mengindikasikan persentase balita mendapat ASI eksklusif semakin tinggi, sedangkan warna yang semakin terang memngindikasikan bahwa persentase balita mendapat ASI eksklusif semakin rendah. Pada tahun 2018, persentase balita mendapat ASI eksklusif tertinggi sebesar 78,6 persen pada Kabupaten Gianyar dan
terendah sebesar 61,9 persen pada Kabupaten Tabanan dan Kota Denpasar. Kota Denpasar termasuk salah satu kabupaten/kota yang maju namun memiliki persentase ASI eksklusif terendah. Hal ini diduga karena ibu – ibu di wilayah Denpasar cenderung merupakan seorang pekerja.
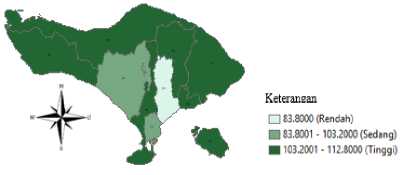
Gambar 6 Persentase Pelayanan Kesehatan Balita di Provinsi Bali tahun 2018
Pada tahun 2018, persentase pelayanan kesehatan balita tertinggi yaitu sebesar 112,8 persen pada Kabupaten Klungkung dan Buleleng sedangkan persentase terendah yaitu sebesar 83,8 pada Kabupaten Gianyar. Semakin gelap warna pada peta mengindikasikan bahwa persentase pelayanan kesehatan balita yang semakin tinggi, dan sebaliknya.
Berdasarkan peta tematik di atas, dapat dibuat rangkuman seperti pada Tabel 3.1 berikut.
Tabel 1. Peringkat Setiap Kabupaten
|
KAB |
Ranking | |||||
|
Yi |
x?.i |
Xsi | ||||
|
JBR |
4 |
1 |
2 |
2 |
2 |
5 |
|
TBN |
6 |
2 |
6 |
9 |
8 |
7 |
|
BDG |
7 |
3 |
8 |
5 |
7 |
6 |
|
GNR |
3 |
5 |
4 |
8 |
1 |
9 |
|
KLK |
5 |
4 |
1 |
1 |
4 |
2 |
|
BLI |
8 |
7 |
5 |
3 |
3 |
4 |
|
KRG |
2 |
9 |
3 |
6 |
5 |
3 |
|
BLL |
1 |
8 |
7 |
7 |
6 |
1 |
|
DPS |
9 |
6 |
9 |
4 |
9 |
8 |
Sumber : Data diolah (2020)
Uji yang digunakan untuk mengetahui ada tidaknya ketergantungan spasial antarlokasi adalah uji Moran’s I dan Uji Lagrange Multiplier.
Tabel 2. Uji Autokorelasi dengan Moran’s I
|
Uji |
Moran’s I |
Value |
Prob. | |
|
Moran’s (error) |
I |
-0,166 |
0,247 |
0,805 |
|
Zo, = 1,96 | ||||
|
E(I) = -0,125 | ||||
Sumber : Data diolah (2020)
Tabel 3. Nilai Moran’s I untuk Setiap Variabel
|
Variabel |
Keterangan |
Moran’s I |
|
ln Y ∖ |
Jumlah Balita gizi buruk |
-0,105 |
|
Xi |
Persentase balita usia 6 – 59 bulan yang mendapat vitamin A |
0,024 |
|
X2 |
Persentase bayi dengan Berat Badan Lahir Rendah (BBLR) |
0,175 |
|
χ2 |
Persentase rumah tangga ber-PHBS |
-0,287 |
|
X4 |
Persentase balita mendapat ASI eksklusif |
-0,122 |
|
X5 |
Persentase Pelayanan Kesehatan Balita |
0,095 |
|
/o = -0,125 | ||
|
a = 0,05 | ||
Sumber : Data diolah (2020)
Tabel 4. Hasil Uji Lagrange Multiplier
|
Uji Kebergantungan Spasial |
Value |
Prob. |
Keputusan |
|
Lagrange Multiplier (lag) |
5,596 |
0,018 |
Tolak H0 ∖ |
|
Lagrange Multiplier (error) |
5,197 |
0,023 |
Tolak H0 ∖ |
|
a = 0,05 | |||
Sumber : Data diolah (2020)
Berdasarkan hasil pada Tabel 4.4 diperoleh nilai p-value untuk Lagrange Multiplier (lag) dan Lagrange Multiplier (error) kurang dari a = 0,05 sehingga tolak Hq , yang berarti terdapat ketergantungan spasial pada lag dan juga pada error. Oleh karena itu, analisis dilanjutkan ke pemodelan menggunakan SAR dan SEM.
Metode yang digunakan dalam pembentukan matriks pembobot spasial yaitu Queen Contiguity. Berikut merupakan matriks ketetanggaan untuk unit pengamatan kabupaten di Provinsi Bali.
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
10 |
|
1 |
0 |
1 |
0 |
0 |
0 |
0 |
10 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
11 |
|
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 1⎟ |
|
W=⎜0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 0⎟ |
|
⎜0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 0⎟ |
|
⎜0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 0⎟ |
|
1 |
1 |
1 |
0 |
0 |
1 |
1 |
00 |
|
0 |
0 |
1 |
1 |
0 |
0 |
0 |
00 |
Matriks di atas kemudian distandarisasi diperoleh matriks pembobot spasial sebagai berikut.
|
0 ∕ 0,33 |
0,5 |
0 |
0 |
0 |
0 |
0 |
0,5 |
00 | |
|
0 |
0,33 |
0 |
0 |
0 |
0 |
0,33 | |||
|
0 |
0,2 |
0 |
0,2 |
0 |
0,2 |
0 |
0,2 |
0,2 | |
|
0 |
0 |
0,25 |
0 |
0,25 |
0,25 |
0 |
0 |
0,25 | |
|
W∗= |
0 |
0 |
0 |
0,33 |
0 |
0,33 |
0,33 |
0 |
0 |
|
⎜0 |
0 |
0,2 |
0,2 |
0,2 |
0 |
0,2 |
0,2 |
0⎟ | |
|
0 |
0 |
0 |
0 |
0,33 |
0,33 |
0 |
0,33 |
0⎟ | |
|
0,2 0 |
0,2 |
0,2 |
0 |
0 |
0,2 |
0,2 |
0 |
0 0 | |
|
0 |
0,5 |
0,5 |
0 |
0 |
0 |
0 | |||
Analisis seanjutnya yaitu menduga parameter berdasarkan metode maximum likelihood.
Tabel 5. Pendugaan Parameter SAR
|
Parameter |
Estimasi Parameter |
Standard Error |
Wald |
P value |
|
P |
-0,509 |
0,445 |
-1,144 |
0,253 |
|
β0 |
607,463 |
191,679 |
3,169 |
0,002 |
|
βl |
-6,166 |
1,875 |
-3,288 |
0,001 |
|
β2 |
1,384 |
2,933 |
0,472 |
0,637 |
|
β3 |
-0,372 |
0,401 |
-0,928 |
0,353 |
|
β4 |
0,520 |
0,558 |
0,933 |
0,351 |
|
β5 |
0,132 |
0,237 |
0,559 |
0,576 |
|
a = 0,05 | ||||
|
R2a |
= 76,21% | |||
|
AIC = 65,11 | ||||
Sumber: Data diolah (2020)
Model SAR yang diperoleh yaitu :
̂i = -0,509Ŵj + 607,463 - 6,166Xu
+1,384X2i - 0,372Xli + 0,520X4i (6)
+ 0,132χii
Dapat dilihat bahwa dalam model penuh SAR, terdapat satu variabel yang signifikan yaitu ^l . Namun, tidak menutup kemungkinan terdapat variabel lain yang signifikan jika dilakukan pembentukan model parsial SAR.
Analisis dilanjutkan dengan membentuk model parsial SAR kemudian melihat nilai AIC terkecil dari semua kemungkinan model yang terbentuk.
Tabel 6. Nilai AIC dan R2 dari Semua Kemungkinan Model
|
No |
Variabel Bebas |
R2 |
AIC |
|
1 |
Xl |
51,59% |
63,083 |
|
2 |
X3 |
32,77% |
66,376 |
|
3 |
X3 |
6,22% |
68,954 |
|
4 |
*4 |
11,78% |
68,423 |
|
5 |
Xs |
14,31% |
68,509 |
|
6 |
dan ^2 |
74,09% |
60,085 |
|
7 |
^l dan ^3 |
51,91% |
65,011 |
|
8 |
^l dan ^4 I |
66,82% |
61,696 |
|
9 |
^l dan X$ |
51,49% |
65,079 |
|
10 |
^2 dan X^ I |
34,88% |
68,046 |
|
11 |
^2 dan X4 I |
36,33% |
68,090 |
|
12 |
^2 dan X$ |
42,99% |
67,567 |
|
13 |
X^ dan X4 I |
21,81% |
69,290 |
|
14 |
X^ dan X$ |
52,38% |
69,754 |
|
15 |
^4 dan Xr1 I |
23,37% |
69,559 |
|
16 |
*1 , x?. dan X3 \ |
74,32% |
61,975 |
|
17 |
*1 , X?. dan *4 \ |
74,03% |
61,992 |
|
18 |
X1 , x?. dan X^ |
74,16% |
62,084 |
|
19 |
X1 , X3 dan *4 \ |
73% |
61,772 |
|
20 |
X1 , X3 dan X5 \ |
52,03% |
67,008 |
|
21 |
Xl , *4 dan X3 \ |
66,73% |
63,649 |
|
22 |
X?. , X3 dan *4 \ |
35,95% |
70,006 |
|
23 |
X?. , Xs dan X3 \ |
50,46% |
68,573 |
|
24 |
X?. , *4 dan X3 \ |
45,55% |
69,362 |
|
25 |
Xs , X4 dan X3 \ |
47,41% |
68,597 |
|
26 |
*1 , X2 , Xs dan *4 |
74,82% |
63,391 |
|
27 |
Xi , X2 , X3 dan X3 |
74,87% |
63,935 |
|
28 |
Xγ , ^2 , X4 dan X3 |
74,05% |
63,992 |
|
29 |
Xγ , ^3 , X4 dan X3 |
75,13% |
63,315 |
|
30 |
X2 , X3 , X4 dan X3 |
50,66% |
70,333 |
Sumber : Data diolah (2020)
Diperoleh bahwa model dengan nilai AIC terkecil yaitu model ke – 6 dengan nilai AIC sebesar 60,085 dan R2 sebesar 74,09%. Meskipun model ke - 6 bukan model dengan nilai R2 terbesar, namun hanya dengan menggunakan dua variabel bebas mampu menghasilkan nilai R2 yang tidak berbeda jauh dengan model yang memiliki nilai R2 terbesar. Oleh karena itu, model terbaik yang dipilih yaitu model ke – 6, dengan variabel bebas yang digunakan yaitu ^l dan ^2 . Selanjutnya dilakukan pemodelan SAR dengan variabel bebas ^l dan ^2 .
Model terbaik yang diperoleh yaitu :
̂i = -0,589Ŵj + 626,984
- 6,224Xli (7)
+ 3,815X2i
Tabel 7. Pemodelan SAR dengan Variabel ^l dan ^2
|
Parameter |
Estimasi Parameter |
Standard Error |
Wald |
P value |
|
P |
-0,589 |
0,355 |
-1,658 |
0,097 |
|
β0 |
626,984 |
167,525 |
3,743 |
0,000 |
|
βl |
-6,224 |
1,677 |
-3,711 |
0,000 |
|
β2 |
3,815 |
1,449 |
2,632 |
0,008 |
|
a = 0,05 | ||||
|
Ra = 74,09% | ||||
|
AIC = 60,085 | ||||
Sumber : Data diolah (2020)
Analisis selanjutnya yaitu melakukan pendugaan parameter SEM.
Tabel 8. Pendugaan Parameter SEM
|
Parameter |
Estimasi Parameter |
Standard Error |
Wald |
P value |
|
λ |
-1,495 |
0,141 |
-10,592 |
0,000 |
|
β0 |
977,465 |
239,140 |
4,087 |
0,000 |
|
βl |
-8,751 |
2,168 |
-4,037 |
0,000 |
|
β2 |
3,127 |
2,201 |
1,421 |
0,155 |
|
β3 |
-1,138 |
0,418 |
-2,723 |
0,006 |
|
β4 |
0,315 |
0,581 |
0,542 |
0,588 |
|
β3 |
-0,333 |
0,212 |
-1,568 |
0,117 |
|
a = 0,05 | ||||
|
Ra = 91,42% | ||||
|
AIC = 62,45 | ||||
Sumber : Data diolah (2020)
Model SEM yang diperoleh yaitu :
̂i = -1,495Ŵj + 977,465 - 8,751Xli +3,127X2i - 1,138Xli + 0,315X4i (8)
- 0,333Xsi
Pada model penuh SEM diperoleh dua variabel bebas yang signifikan. Akan tetapi, tidak menutup kemungkinan terdapat variabel bebas lainnya yang signifikan jika dilakukan pembentukan model parsial SEM.
Selanjutnya akan dilakukan pembentukan model parsial SEM dan melihat nilai AIC terkecil dari semua kemungkinan model yang terbentuk. Diperoleh bahwa model dengan nilai R2 terbesar yaitu model ke – 27 dengan nilai R2 sebesar 96,24% dan AIC sebesar 60,837. Meskipun model ke - 27 bukan model dengan nilai AIC terkecil, namun hanya dengan
menggunakan empat variabel bebas mampu menghasilkan nilai AIC yang tidak berbeda jauh dengan model yang memiliki nilai AIC terkecil. Oleh karena itu, model terbaik yang dipilih yaitu model ke – 27, dengan variabel bebas yang digunakan yaitu ^l , ¾ , ^3 , dan ¾ . Selanjutnya dilakukan pemodelan SEM dengan variabel bebas ^l , ^2 ,X3 , dan ¾ .
Model terbaik yang diperoleh yaitu:
̂i = -2,252Ŵj + 919,691 - 8,123Xli
+3,858X2i - 0,982Xli - 0,306Xsi
(9)
Tabel 11. Ukuran Kebaikan Model SAR dan SEM
Tabel 9. Nilai AIC dan R2 dari Semua Kemungkinan Model
|
No |
Variabel Bebas |
R2 |
AIC |
|
1 |
*1 |
58,57% |
60,372 |
|
2 |
*2 |
34,96% |
64,189 |
|
3 |
*3 |
6,24% |
66,957 |
|
4 |
*4 |
10,68% |
66,490 |
|
5 |
*5 |
36,04% |
63,704 |
|
6 |
dan %2 I |
70,06% |
59,334 |
|
7 |
dan X3 I |
62,78% |
61,930 |
|
8 |
dan X4 |
64,51% |
60,187 |
|
9 |
dan ^5 |
60,18% |
62,316 |
|
10 |
%2 dan X3 I |
46,61% |
65,212 |
|
11 |
%2 dan ¾ |
41,89% |
64,395 |
|
12 |
%2 dan ¾ |
53,65% |
64,199 |
|
13 |
X3 dan X4 |
21,96% |
67,283 |
|
14 |
X3 dan ¾ |
40,12% |
65,469 |
|
15 |
X4 dan ¾ |
44,10% |
65,293 |
|
16 |
¾ , ¾ dan X3 |
69,80% |
59,153 |
|
17 |
Xj , ^2 dan X4 |
70,44% |
61,332 |
|
18 |
¾ , ¾ dan χ≡ |
70,16% |
60,977 |
|
19 |
^l , X3 dan ¾ |
68,18% |
58,854 |
|
20 |
¾ , ¾ dan χ≡ |
65,13% |
63,762 |
|
21 |
^l , X4 dan ¾ |
64,97% |
61,999 |
|
22 |
X'2 , ^3 dan X4 |
44,74% |
66,332 |
|
23 |
¾ , ¾ dan Xs |
56,92% |
64,973 |
|
24 |
X'2 , X4 dan ^5 |
43,41% |
65,548 |
|
25 |
*3 , ¾ dan Xs |
60,35% |
65,398 |
|
26 |
X1 , *2 , *3 dan ¾ |
55,88% |
60,480 |
|
27 |
^1 , *2 , *3 dan X5 |
96,24% |
60,837 |
|
28 |
*1 , *2 , X4 dan Xs ∖ |
69,85% |
62,973 |
|
29 |
*1 , *3 , *4 dan Xs ∖ |
58,93% |
60,789 |
|
30 |
X2 , *3 , *4 dan x5 ∖ |
56,24% |
66,965 |
Sumber : Data diolah (2020)
Tabel 10. Pemodelan SEM dengan Variabel ¾ , X2 , ¾ , dan *5
|
Parameter |
Estimasi Parameter |
Standard Error |
Wald |
P value |
|
λ |
-2,252 |
0,008 |
-270,31 |
0,000 |
|
βo |
919,691 |
177,801 |
5,173 |
0,000 |
|
βl |
-8,123 |
1,585 |
-5,124 |
0,000 |
|
β2 |
3,858 |
0,643 |
5,996 |
0,000 |
|
β3 |
-0,982 |
0,141 |
-6,969 |
0,000 |
|
-0,306 |
0,145 |
-2,107 |
0,035 | |
|
a = 0,05 | ||||
|
Ra = 96,24% | ||||
|
AIC = 60,837 | ||||
Sumber : Data diolah (2020)
|
No. |
Model |
AIC |
R2 |
|
1 |
SAR |
60,085 |
74,09% |
|
2 |
SEM |
60,837 |
96,24% |
Sumber : Data diolah (2020)
Diperoleh bahwa model dengan R2 terbesar yaitu model SEM. Meskipun nilai AIC dari model SEM bukan yang terkecil, namun nilai AIC dari model SEM tidak berbeda jauh dengan model lainnya. Oleh karena itu, model terbaik yang dipilih untuk memodelkan kasus balita gizi buruk di Provinsi Bali adalah model SEM dengan AIC sebesar 60,837 dan R2 sebesar 96,24%. Nilai R2 sebesar 96,24% menunjukkan bahwa variabel - variabel bebas yang digunakan mampu menjelaskan variabel terikat sebesar 96,24% dan sisanya yaitu sebesar 3,76% dijelaskan oleh variabel lain diluar model.
-
3.9 Matriks Spatial Error
Hasil kali W dengan vektor residual, disebut juga sebagai spatial error, merepresentasikan rataan residual pada wilayah yang didefinisikan sebagai tetangga pada matriks W. Lebih jelasnya, spatial error untuk 9 kabupaten/kota di Provinsi Bali pada tahun 2018 adalah sebagai berikut:
|
∕ ∖ TBN ∣ |
⎛ |
0 0,33 |
0,5 0 |
0 0,33 |
0 0 |
0 0 |
0 0 |
0 0 |
0,5 0,33 |
0 0 |
-10,1,09171 |
|
BDG |
⎜ |
0 |
0,2 |
0 |
0,2 |
0 |
0,2 |
0 |
0,2 |
0,2 |
-2,761 |
|
⎜ GNR ⎟ |
0 |
0 |
0,25 |
0 |
0,25 |
0,25 |
0 |
0 |
0,25 2,779 | ||
|
⎜ KLK ⎟= |
0 |
0 |
0 |
0,33 |
0 |
0,33 |
0,33 |
0 |
0 |
⎟⎜-2,307⎟ | |
|
⎜ BLI ⎟ |
⎜ |
0 |
0 |
0,2 |
0,2 |
0,2 |
0 |
0,2 |
0,2 |
0 |
⎟⎜ 0,075 ⎟ |
|
⎜ KRG ⎟ |
⎜ |
0 |
0 |
0 |
0 |
0,33 |
0,33 |
0 |
0,33 |
0 |
⎟⎜ 0,783 ⎟ |
|
∖ BLL |
0,2 |
0,2 |
0,2 |
0 |
0 |
0,2 |
0,2 |
0 |
0 |
0,199 | |
|
^DPS' |
∖ |
0 |
0 |
0,5 |
0,5 |
0 |
0 |
0 |
0 |
0 |
0,046 |
0,094
-0,45 0,618
-1,237
⎜ 1,2
⎜ 0,365
⎜-0,671
-0,144 0,009
Jika dilihat perbandingan antara vektor spatial error dan vektor residual yang sebenarnya, diperoleh bahwa terdapat 3 kabupaten yang memiliki selisih yang positif yaitu BDG, KLK, dan BLI. Sedangkan kabupaten/kota lainnya memiliki selisih yang negatif. Nilai spatial
error yang positif mengindikasikan bahwa kabupaten tersebut mendapat ‘keuntungan’ dari tetangganya dalam membentuk angka gizi buruk pada balita, sedangkan nilai yang negative mengindikasikan bahwa kabupaten tersebut ‘mendukung’ tetangganya atau membawa pengaruh bagi tetangganya.
Model regresi yang diperoleh adalah model SEM dengan persamaan :
̂i = -2,252Ŵj + 919,691 - 8,123Xli +3,858X2i - 0,982⅛i - 0,306X^i
Berikut merupakan interpretasi dari model SEM yang diperoleh.
-
1. Koefisien lambda (λ) signifikan pada taraf kepercayaan 5% artinya terdapat keterkaitan antara kasus balita gizi buruk pada suatu wilayah dengan wilayah lainnya yang berdekatan.
-
2. Koefisien ̂ = -8,123 menunjukkan
bahwa kenaikan persentase balita usia 6 – 59 bulan yang mendapat vitamin A sebesar satu satuan, maka dapat menurunkan jumlah kasus balita gizi buruk sebesar 8,123 satuan apabila faktor lain dianggap konstan.
-
3. Koefisien ̂2 = 3,858 menunjukkan bahwa kenaikan persentase bayi dengan Berat Badan Lahir Rendah (BBLR) sebesar satu satuan, maka dapat meningkatkan jumlah kasus balita gizi buruk sebesar 3,858 satuan apabila faktor lain dianggap konstan.
-
4. Koefisien ̂3 = -0,982 menunjukkan
bahwa kenaikan persentase rumah tangga ber-PHBS sebesar satu satuan, maka dapat menurunkan jumlah kasus balita gizi buruk sebesar 0,982 satuan apabila faktor lain dianggap konstan.
-
5. Koefisien ̂5 = -0,306 menunjukkan
bahwa kenaikan persentase pelayanan kesehatan balita sebesar satu satuan, maka dapat menurunkan jumlah kasus balita gizi buruk sebesar 0,306 satuan apabila faktor lain dianggap konstan.
Berdasarkan penjelasan di atas diperoleh bahwa terdapat ketergantungan spasial pada lag dan juga pada error. Oleh karena itu, dilakukan
pemodelan Spatial Autoregressive Model (SAR) dan Spatial Error Model (SEM) kemudian dilakukan perbandingan antara model – model yang diperoleh. Model terbaik yang diperoleh adalah model SEM dengan AIC sebesar 60,837 dan R2 sebesar 96,24%. Adapun faktor – faktor yang berpengaruh signifikan terhadap kasus balita gizi buruk yaitu persentase balita usia 6 – 59 bulan yang
mendapat vitamin A, persentase bayi dengan Berat Badan Lahir Rendah (BBLR), persentase rumah tangga ber-PHBS, dan persentase pelayanan kesehatan balita.
Berdasarkan penjelasan yang telah diuraikan di atas, saran untuk penelitian selanjutnya diharapkan mempertimbangkan data time series sehingga dapat dianalisis menggunakan data panel spasial dan pemerintah diharapkan mampu meningkatkan persentase balita usia 6 – 59 bulan yang
mendapat vitamin A, mengurangi persentase bayi dengan Berat Badan Lahir Rendah (BBLR), meningkatkan persentase rumah tangga ber-PHBS, dan juga meningkatkan cakupan pelayanan kesehatan balita.
DAFTAR PUSTAKA
Anselin, L., Rey, S. J. & Florax, R. J., 2004. Advances in Spatial Econometrics. Heidelberg: Springer.
Draper, N. R. & Smith, H., 1998. Applied
Regression Analysis: Third Edition.
Canada: John Wiley & Sons, Inc.
Jayanti, S., Sumarjaya, I. W. & Susilawati, M., 2017. Pemodelan Penyebaran Kasus Demam Berdarah Dengue (DBD) di Kota Denpasar dengan Metode Spatial Autoregressive (SAR). E-Jurnal
Matematika, 6(1), pp. 37 - 46.
Kemenkes, 2017. Buku Saku Pemantauan Status Gizi Tahun 2017. Jakarta: Kementerian Kesehatan Republik
Indonesia.
LeSage, J. & Pace, R. K., 2009. Introduction to Spatial Econometrics. New York: CRC Press.
Profil Kesehatan Provinsi Bali, 2019. Profil Kesehatan Provinsi Bali. s.l.:Dinas Kesehatan Provinsi Bali.
110
Discussion and feedback