GRAF DUAL ANTIPRISMA DAN DIMENSI METRIKNYA
on
E-Jurnal Matematika Vol. 10(1), Januari 2021, pp. 6-11
DOI: https://doi.org/10.24843/MTK.2021.v10.i01.p313
ISSN: 2303-1751
GRAF DUAL ANTIPRISMA DAN DIMENSI METRIKNYA
Fenny Fitriani1§, Sari Cahyaningtias2
1Universitas PGRI Adi Buana, Jl. Dukuh Menanggal XII No. 4, Surabaya [fenny_f@unipasby.ac.id] 2Universitas PGRI Adi Buana, Jl. Dukuh Menanggal XII No. 4, Surabaya [sari@unipasby.ac.id] §Corresponding Author
ABSTRACT
Dual graph is one form of graph that can only be formed from graphs whose edges do not intersect each other. One of the graphs that can be converted into dual graphs is the antiprism graph ^m . Antiprism graph ^m is a graph that is formed from the absorption of vertices in the prism graph ^m . One of the operations performed on a graph is finding the metric dimension of the graph. These metric dimensions are used to find a minimum cardinality value of the graph. This article discusses of general form of the dual antiprism graph , and the metric dimensions of it. The metric dimensions of dual antiprism graph , is obtained in four conditions. The first condition of metric dimension is when , . The second condition of metric dimension is when , with n≥3. The third condition of metric dimension is when , with n≥3. The last condition of metric dimension is when , with m≥5 andn≥3
Keywords: antiprism graph, dual graph, metric dimension.
Graf dual merupakan graf yang dibentuk dari mengubah region graf pembentuk menjadi simpul dari graf dual dan simpul-simpul yang terbentuk akan dihubungkan oleh suatu sisi apabila region yang direpresentasikan oleh simpul saling dipisahkan secara langsung dengan suatu sisi dari graf pembentuk (Bondy 1976). Dengan kata lain, graf dual hanya dapat dibentuk apabila sisi-sisi graf pembentuk graf dual tidak saling berpotongan. Graf antiprisma ^m merupakan salah satu bentuk graf yang dapat dibentuk ke dalam graf dual.
Graf antiprisma ^m sendiri merupakan graf yang dibentuk dari pelengkapan sisi graf prisma ^m dengan sisi , , dengan nilai i dan j
yang memenuhi berada pada rentang 1≤i≤ m-1 dan 1≤j≤n-1 serta sisi , ,
dengan nilai j yang memenuhi berada pada rentang 1≤j≤n-1 (Baca & Miller, 2008).
Beberapa penelitian dengan menggunakan subjek penelitian graf antiprisma telah beberapa kali dilakukan. Apriliani (2016) melakukan penelitian mengenai dimensi partisi pada graf antiprisma. Khoiriah dan Kusmayadi (2018) melakukan penelitian mengenai dimensi metrik lokal pada graf antiprisma dan graf sun.
Sholihah (2016) melakukan penelitian mengenai dimensi metrik pada beberapa graf khusus.
Dimensi metrik dari graf didapatkan apabila didapatkan nilai kardinilitas minimum dari himpunan pembeda dari graf pembentuk. Beberapa penelitian yang berhubungan dengan dimensi metrik antara lain penelitian mengenai analisis dimensi metrik dan himpunan pembeda jika dihubungkan keterampilan berpikir tingkat tinggi yang diteliti oleh Sulistio, Slamin, dan Dafik (2015), penelitian mengenai pencarian dimensi metrik dari famili graf tangga yang diteliti oleh Saifudin (2016), penelitian mengenai pencarian dimensi metrik dari graf Wn + Cn dengan nilai n ∈ {3,4} yang diteliti oleh Putra, Yulianti, dan SY (2018), penelitian mengenai pencarian dimensi metrik pada graf buku ganda yang diteliti oleh Ilmayasinta, (2019), penelitian mengenai pencarian dimensi metrik hasil operasi tertentu pada petersen yang diperumum yang diteliti Aldino (2019), dan penelitian mengenai pencarian dimensi metrik pada penghapusan satu simpul dari graf dual prisma yang diteliti oleh Fitriani (2019).
Dari penjelasan di atas, maka dalam artikel ini dibahas bentuk umum dari graf dual
antiprisma yang terbentuk dari graf antiprisma serta pencarian dimensi metrik dari graf dual yang terbentuk.
Pada penelitian ini, graf yang digunakan dalam membentuk graf dual adalah graf antiprisma ^m . Langkah-langkah yang
dilaksanakan dalam penelitian ini dapat dijabarkan sebagai berikut:
-
a) Mengubah graf antiprisma ^m ke dalam bentuk graf dualnya.
-
b) Menentukan batas bawah dan batas atas dari dimensi metrik graf dual
-
c) Menentukan nilai dari dimensi metrik graf dual yang terbentuk dari graf antiprisma An
Dari hasil penelitian yang telah dilakukan, berikut diberikan definisi dari graf dual yang dibentuk dari graf antiprisma ^m
Definisi 3.1 Graf , merupakan graf dual yang terbentuk dari graf antiprisma ^m dimana region dari graf antiprisma merupakan simpul dari graf dual antirpisma dan sisi yang menghubungkan dua simpul dari graf dual antiprisma terbentuk jika region dari graf antiprisma yang direpresentasikan oleh simpul saling dipisahkan secara langsung dengan suatu sisi
Graf dual antiprisma , yang
didefinisikan tersebut memiliki himpunan simpul V( , )={ , |1≤i≤ m dan1≤
j≤2n-2}∪{Uq, un } dengan himpunan sisi E(^m ,n)={Ui,jUi,7 + 1|1≤i≤ m dan1≤j≤ 2n-2}∪{ , , |1≤i< m dan1≤
j<n}∪{ , |1≤i≤m}∪
{Um ,2iu1,2i-1|1≤i<n}∪{UγlU^,2n-2|1≤i≤ m}. Dari himpunan sisi dan himpunan simpul graf dual antiprisma , tersebut, didapatkan |E(^m ,n)|=m(3n-2) dan |V(^m ,n)|= 2m(n-1)+2.
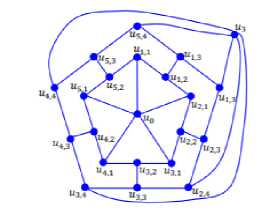
Gambar 1. Graf dual antiprisma ,
Satu contoh dari graf dual antiprisma , adalah graf dual antiprisma , yang
ditunjukkan pada Gambar 1. Graf dual
antiprisma pada Gambar 1 terbentuk dari graf antiprisma ^5. Himpunan simpul dari graf , adalah V(^5 ,3)={wO , U3}∪{Ui,j|i≤i≤
-
5 dan1≤j ≤4} dengan himpunan simpul E(^5 ,3)={Ui,j Ui,j+1|1≤i≤5dan1≤j≤ 4}∪{Ui,2]Ui+ι,27-1|1≤i<5dan1≤j< 3}∪{UqU^,1|1≤i≤5}∪{U3,2iul,2i-l|1≤ i<3}∪{ , |1≤i≤5}.
Dari definisi graf dual antiprisma , yang didapatkan di atas, dimensi metrik dari graf dual antiprisma , didapatkan dalam empat keadaan yaitu dimensi metrik dari , , dimensi metrik dari , dengan n≥3,
dimensi metrik dari , dengan m≥5 dan n≥3.
Dimensi metrik graf dual antiprisma ,
Pada graf dual antiprisma , , didapatkan himpunan simpul dari graf V(
{, |1≤i≤ m dan1<j ≤2}∪{UqU2 } dan himpunan sisi dari graf E(
{ Ui ,Iui,2|1≤i≤m}∪{Ui ,2ui + l,1|1≤i< m}∪{ , |1≤i≤m}∪{ , |1≤i≤
m}∪{ , , }. Dari himpunan simpul dan
himpunan sisi tersebut maka didapatkan |V(^m ,2)|=2m+2 dan |E(^m ,2)|=4m.
Dimensi metrik dari graf dual antiprisma , didapatkan pada tiga keadaan, yaitu pada saat m=3,m=4, dan m≥5. Berikut
merupakan teorema yang menunjukkan nilai dari dimensi metrik graf dual antiprisma ,
Teorema 3.2 Jika graf dual antiprisma graf , merupakan graf dual yang terbentuk dari graf antiprisma ^m , maka
m, untuk m=3atau m=4 m-1, untukm≥5
dim ( ^m ,2)={
Bukti:
Dalam pembuktian dim ( ,) =m untuk
m=3atau m=4 mudah untuk didapatkan himpunan W sehingga hasil representasi setiap simpul u∈V( , ) terhadap himpunan W
berbeda. Atau dengan kata lain mudah untuk didapatkan dim ( , )≤m . Dengan
mengambil salah satu simpul yang ada pada himpunan W, maka hasil representasi dari simpul u∈V( , ) terhadap himpunan W
terdapat hasil representasi yang sama. Sehingga dim ( , )≥m . Karena m≤ , ≤
m , sehingga dim ( ,) =m untuk =
3 atau m=4.
Untuk pembuktian dim ( ,) =m-1 untuk
m≥5, untuk mendapatkan batas atas dimensi metrik yaitu dim ( , )≤m-1 maka
pembuktian dilakukan pada dua keadaan yaitu jika m merupakan bilangan gasal dan jika m merupakan bilangan genap.
Jika m bilangan gasal
Untuk m merupakan bilangan gasal, jika dimisalkan himpunan pembeda W yang diambil adalah W={ , , , |1≤i<
⌈ ⌉} yang memuat m-1 simpul maka didapatkan hasil representasi setiap simpul u∈V( , ) berbeda. Atau dapat dituliskan
dim ( ,) ≤m-1.
Jika m bilangan genap
Untuk m merupakan bilangan genap, jika dimisalkan himpunan pembeda W yang diambil adalah W={ , , , |1≤i<
}∪{ , } yang memuat m-1 simpul
maka didapatkan hasil representasi setiap simpul u∈V( , ) berbeda. Atau dapat
dituliskan dim ( ,) ≤m-1.
Untuk pembuktian batas bawah yaitu
dim ( ,) ≥m-1. Jika dimisalkan
dim ( ,) =m-2 maka: (i) jika himpunan
pembeda W memiliki anggota himpunan adalah , dengan 1≤i≤m-2, maka dapat ditemukan hasil representasi yang sama dari simpul , dan simpul , terhadap
himpunan pembeda W; (ii) jika himpunan pembeda W memiliki anggota himpunan adalah , dengan 1≤i≤m-2, maka dapat ditemukan hasil representasi yang sama dari
simpul , dan simpul , terhadap
himpunan pembeda W; (iii) jika m-2 yang diambil adalah genap dengan himpunan pembeda W ={ , , , |i≠j }, maka dapat
ditemukan hasil representasi yang sama dari simpul , dan simpul , terhadap himpunan pembeda W dengan a≠b ; (iv) jika m-2 yang diambil adalah genap dengan himpunan pembeda W ={ , , , |i= }, maka dapat
ditemukan hasil representasi yang sama dari simpul , dan simpul , terhadap himpunan pembeda W dengan a≠b . Dari beberapa himpunan W tersebut didapat kardinalitas dari |W|≥m-1, atau dengan kata lain dim ( , )≥m-1 .
Karena m-1≤dim ( , )≤m-1 , maka
didapatkan dim ( , )=m-1 ․ ∎
Dimensi metrik graf dual antiprisma , dengan n≥3
Berikut merupakan teorema yang menunjukkan nilai dari dimensi metrik graf dual antiprisma , dengan n≥3
Teorema 3.3 Jika graf dual antiprisma graf , merupakan graf dual yang terbentuk dari graf antiprisma A2 dengan n≥3, maka dim (^3 ,n) =2⌊ 3⌋+2
Bukti:
Misalkan himpunan bilangan pembeda yang diambil adalah W ={ , , , |1≤i<
⌊I⌋ untuk. ⌊I⌋>1}∪
{ U1 ,1, U2,1U1,2n-3, U2,2n-3}. Jika n yang diambil adalah n mod3≡0 ataun mod3≡1, maka didapatkan hasil representasi setiap simpul u∈V(, ) berbeda. Jika n yang diambil adalah n mod3≡2, maka hasil representasi simpul untuk simpul-simpul sikel terluar dari graf memiliki hasil yang sama. Sehingga untuk n mod3≡2, jika himpunan bilangan pembeda yang diambil adalah W={ , , , |1≤
. _ n—2 ι 1 n—2 ) i i
i< — untuk —>1 }∪
3 3 J
{ U1 ,3, U2,3, U1 ,2n-5, U2,2n-5} menyebabkan hasil representasi setiap simpul U∈V(,)
berbeda. Kardinalitas dari himpunan pembeda W tersebut adalah 2⌊⌋+2. Karena hasil
representasi tiap simpul berbeda, maka
dim (^3 ,n) ≤2⌊ ? ⌋+2.
Misalkan kardinalitas dari himpunan W terdiri atas 2⌊⌋+1, maka (i) jika himpunan W dibentuk dari satu simpul dari 2⌊ ⌋+1 sikel yang berbeda pada graf dual, maka dapat ditemukan hasil representasi simpul yang sama terhadap himpunan W; (ii) jika terdapat dua sampai tiga simpul dari himpunan W diambil dari sikel yang pertama, maka dapat ditemukan hasil representasi simpul yang sama terhadap himpunan W . Dari kondisi (i) dan (ii) tersebut, maka kardinalitas dari himpunan W harus lebih dari 2⌊?⌋+1 atau |W|≥2⌊?⌋+2. Sehingga didapatkan dim (, ) ≥2⌊ ⌋+2.
Karena 2⌊ 3⌋+2≤dim (, ) ≤2⌊3⌋+2,
maka dim (, ) =2⌊ ⌋+2.
∎
Dimensi metrik graf dual antiprisma , dengan n≥3
Berikut merupakan teorema yang menunjukkan nilai dari dimensi metrik graf dual antiprisma , dengan n≥3
Teorema 3.4 Jika graf dual antiprisma graf , merupakan graf dual yang terbentuk dari graf antiprisma A™ dengan n≥3, maka
dim (⅛ ,n) =⌈ ⌉+1
Bukti:
Misalkan diambil
himpunan bilangan pembeda yang
W={u1 ,2, U4 ,2}∪ ∪
adalah
{ U4 ,6(2i-l)|1≤i≤⌊ 6 ⌋}
{u2,6i+4 |iganjil pada 1≤i≤k}∪
{u2,6i+2 |igenap pada 1≤i≤k}∪
{, |n mod3≡1 ataunmod3≡
2 dan nganjil }∪{ , | n mod3≡
0 dan n ganjil} dimana untuk n mod6≡0 dan n mod6≡1 nilai k=2⌊⌋-1, sedangkan untuk n mod6≡a dengan a∈{2,3,4,5} nilaik =2⌊6 ⌋. Kardinalitas dari himpunan pembeda Wadalah ⌈⌉+1. Dengan menggunakan himpunan pembeda W tersebut, maka didapatkan hasil representasi setiap simpul u∈V(, ) berbeda, sehingga dim (⅛ ,n)≤ ⌈ ? ⌉+,1.
Misalkan kardinalitas dari himpunan W terdiri
atas ⌈⌉, maka (i) jika himpunanW dibentuk dari satu simpul dari ⌈⌉ sikel yang berbeda pada graf dual, maka dapat ditemukan hasil representasi simpul yang sama terhadap himpunan W; (ii) jika ⌈ ⌉≤4 simpul dari himpunan W diambil dari sikel yang pertama, maka dapat ditemukan hasil representasi simpul yang sama terhadap himpunan W . Dari kondisi (i) dan (ii) tersebut, maka kardinalitas dari himpunan Wharus lebih dari ⌈⌉ atau |W|≥
⌈⌉+1. Sehingga didapatkan dim (,) ⌈Ξ⌉+1. ,
l2 1
Karena didapatkan ⌈⌉+1≤dim (,) ⌈?⌉+1, makadim (A4,n) =⌈Ξ⌉+1.
≥
≤
∎
Dimensi metrik graf dual antiprisma , dengan m≥5 dann≥3
Dimensi metrik dari graf dual antiprisma , didapatkan pada dua keadaan, yaitu pada saat n= +i dengan 1≤i<m dan n≥
2m. Berikut merupakan teorema yang
menunjukkan nilai dari dimensi metrik graf dual antiprisma , dengan m≥5 dann≥3
Teorema 3.5 Jika graf dual antiprisma graf
, merupakan graf dual yang terbentuk dari graf antiprisma Am dengan m≥5 dann≥3, maka
dim ( ^m ,n)
(2m-4,untuk n = + idengan1≤i<m
I n-3, untuk n≥2m
Bukti:
Pertama akan dibuktikan untuk n= +i dengan 1≤i<m maka dim ( , ) =2m-4․ Misalkan himpunan bilangan pembeda yang diambil adalah W={ , , , |1≤i≤ m-2}. Dengan menggunakan himpunan pembeda W tersebut, maka didapatkan hasil representasi setiap simpul u∈V( ,) berbeda. Kardinilitas dari himpunan pembeda W tersebut adalah 2m-4. Karena hasil representasi tiap simpul berbeda, maka dim ( , ) ≤2m-4.
Misalkan kardinalitas dari himpunan W terdiri atas 2 m-3 dan himpunan W terdiri atas simpul , dengan 1≤i≤m-2 dan m-1
simpul yang lain yang terletak pada sikel yang berbeda. Dari himpunan IV tersebut, maka dapat ditemukan hasil representasi simpul yang sama terhadap himpunan W yaitu terletak pada simpul yang berada pada sikel terluar. Sehingga menyebabkan kardinalitas dari himpunan W harus lebih dari 2 m-3 atau |W|≥2m-4. Dengan kata lain didapatkan dim ( ,) ≥
2m-4, maka didapatkan dim ( ,)=
Selanjutnya, dilakukan pembuktian bahwa untu n≥2m maka dim ( ,) =n-3. Misalkan
himpunan bilangan pembeda yang diambil adalah W={ , , , |1≤i≤m-2}∪
{U1,2(m+i)|0≤i≤2m-n}. Dengan
menggunakan himpunan pembeda W tersebut, maka didapatkan hasil representasi setiap simpul u∈V( , ) berbeda. Kardinilitas dari
himpunan pembeda W tersebut adalah n-3. Karena hasil representasi tiap simpul berbeda, maka dim ( ,) ≤n-3.
Misalkan kardinalitas dari himpunan W terdiri atas n-4, maka (i) jika , atau , untuk
1≤i≤m merupakan bagian dari himpunan W dan sisa simpul dari himpunan W berbada pada sikel yang berbeda-beda, maka dapat ditemukan hasil representasi simpul yang sama terhadap himpunan W; (ii) jika n-4 simpul yang ada pada himpunan W diambil dari sikel yang berbeda, maka dapat ditemukan hasil representasi simpul yang sama terhadap himpunan W. Dari kondisi (i) dan (ii) tersebut menyebabkan kardinalitas dari himpunan W harus lebih dari n-4 atau |W|≥n-3. Dengan kata lain didapatkan dim ( ,) ≥
n-3.
Karena n-3≤dim ( ,) ≤n-3, maka
didapatkan dim ( ,) =n-3. ∎
Berdasarkan uraian pada pembagian pembahasan, maka dapat disimpulkan bahwa:
-
a) Graf dual dari graf antiprisma ^m adalah graf dual antiprisma , dengan jumlah sisi dan simpul dari graf dual antiprisma secara berturut-turut adalah m(3n-2) dan 2m(n-1)+2.
-
b) Dimensi metriks dari graf dual antiprisma didapatkan dalam empat keadaan yaitu
dimensi metrik pada , , dimensi metrik pada , dengan n≥3, dimensi metrik pada , dengan n≥3, dan dimensi metrik pada , dengan m≥5 dann≥3.
Dimensi metrik yang didapatkan pada
empat keadaan tersebut antara lain: i) Dimensi
metrik graf dual antiprisma pada , adalah dim ( ,) =m untuk m=3 atau m=4 dan dim ( ,) =m-1 untuk m≥5; ii)
Dimensi metrik graf dual antiprisma pada ,
dengan n≥3 adalahdim (, ) =2
+2;
iii) Dimensi metrik graf dual antiprisma pada
, dengan n≥3 adalahdim (,)
=⌈ ? ⌉+
1; dan iv) Dimensi metrik graf dual antiprisma pada , dengan m≥5 dan n≥3 adalah dim ( , ) =2m-4 untuk n= + idengan 1≤i<m dan dim ( ,) =n-3 untuk n≥2m.
Dari pembahasan yang telah dijabarkan dan penelitian-penelitian terdahulu, diketahui bahwa masih kurangnya penelitian mengenai graf dual. Sehingga untuk penelitian lebih lanjut, peneliti dapat melakukan suatu penelitian dengan topik pembahasan mengenai graf dual. Salah satu contohnya adalah penelitian mengenai dimensi metrik dari graf dual yang terbentuk dari beberapa jenis graf yang lain.
DAFTAR PUSTAKA
Aldino, A. A. (2019). Dimensi Metrik Hasil Operasi Tertentu Graf Petersen Diperumum. Bandar Lampung: Digilib UNILA.
Apriliani, T. (2016). Dimensi Partisi Pada Graf Antiprisma, Graf Mongolian Tent, dan Graf Stacked Book. Surakarta: UPT Perpustakaan Universitas Sebelas Maret .
Baca, M., & Miller, M. (2008). Super Edge-Antimagic Graphs, a Wealth of Problems and Some Solutions. Boca Raton: BrownWalker Press.
Fitriani, F. (2019, Juli). Dimensi Metrik Penghapusan Satu Simpul Graf Dual
Prisma. MUST: Journal of Mathematics Education, Science and Technology, 4 (1), 108-113.
Ilmayasinta, N. (2019). Dimensi Metrik pada Graf Buku Ganda. Jurnal Pendidikan Matematika dan Matematika, I (01), 21-27.
Khoiriah, S., & Kusmayadi, T. A. (2018). Dimensi Metrik Lokal Pada Graf Antiprisma Dan Graf Sun. Journal of Mathematics and Mathematics Education, 8 (1), 9-15.
Putra, R. N., Yulianti, L., & SY, S. (2018). Dimensi Metrik Dari Graf Wn + Cn, Untuk n 3,4. Jurnal Matematika UNAND, VII (2), 165 – 169.
Saifudin, I. (2016, Agustus). Dimensi Metrik dan Dimensi Partisi dari Famili Graf Tangga. JUSTINDO, Jurnal Sistem & Teknologi Informasi Indonesia, 1 (2), 105112.
Sholihah, W. N. (2016). Dimensi Metrik Dan Non-Isolated Resolving Number Pada Beberapa Graf Khusus. Jember: Digital Repository Universitas Jember.
Sulistio, W., Slamin, & Dafik. (2015). Analisis Dimensi Metrik Dengan Himpunan Pembeda Terhubung Pada Graf Khusus Keluarga Pohon Dikaitkan Keterampilan Berpikir Tingkat Tinggi. Kadikma, 6 (3), 26-35.
11
Discussion and feedback