PERHITUNGAN PREMI TAHUNAN TIDAK KONSTAN DAN CADANGAN BENEFIT ASURANSI LAST SURVIVOR DWIGUNA

E-Jurnal Matematika Vol. 9(2), Mei 2020, pp.104-108

DOI: https://doi.org/10.24843/MTK.2020.v09.i02.p286

ISSN: 2303-1751

PERHITUNGAN PREMI TAHUNAN TIDAK KONSTAN DAN CADANGAN BENEFIT ASURANSI LAST SURVIVOR DWIGUNA

Sani Saefuloh¹, I Nyoman Widana^2§, Luh Putu Ida Harini³

• ¹Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: [email protected]]

• ²Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: [email protected]]

• ³Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: [email protected]]

^§Corresponding Author

ABSTRACT

Last Survivor Insurance is life insurance for two or more participants with premiums paid until the death of the last participant. This study discusses last survivor endowment insurance for two participants in a married couple. Compensation is paid after the second person dies or both stills alive after the end of a contract. The purpose of this study is to determine the value of non-constant annual premium and benefits reserves in the last survivor endowment insurance. The equivalence principle is used for calculation of premiums. Furthermore, the benefit reserve formula is determined using a prospective method. The value of the benefit reserve will continue to increase as long as premium payments are still being made.

Keywords: last survivor insurance, non-constant annual premium, benefit reserves, prospective method.

Asuransi last survivor dwiguna merupakan salah satu jenis asuransi jiwa yang menggabungkan dua manfaat sekaligus dari manfaat asuransi last survivor endowmen murni dengan asuransi last survivor berjangka. Dengan manfaat jika peserta masih hidup sampai akhir kontrak ataupun meninggal dalam jangka waktu kontrak, peserta akan tetap mendapatkan santunan. pada asuransi last survivor premi dibayarkan sampai terjadi kematian terakhir peserta.

Premi merupakan sejumlah uang yang wajib dibayarkan oleh pihak tertanggung kepada pihak penanggung sesuai dengan kontrak asuransi yang telah disepakati. Terdapat beberapa faktor yang harus diperhatikan dalam perhitungan premi asuransi jiwa, yaitu biaya perusahaan, tingkat kematian dan tingkat suku bunga (Sembiring, 1986). Dilihat dari besarnya pembayaran premi, ada dua jenis pembayaran premi, yaitu pembayaran premi konstan dan pembayaran premi tidak konstan.

Jenis pembayaran premi konstan selalu tetap setiap tahunnya sehingga cocok dengan orang berpendapatan tetap. Sedangkan jenis

pembayaran premi tidak konstan lebih diperuntukkan bagi orang yang berpendapatan tidak tetap, dikarenakan penghasilan dari pendapatan yang tidak tetap setiap waktu dapat disesuaikan dengan jenis pembayaran premi tidak konstan yang bisa berubah setiap waktu.

Pendapatan perusahaan asuransi diperoleh dari pembayaran premi. Pada awal kontrak asuransi pendapatan tersebut jauh lebih besar dari pada jumlah uang pertanggungan yang harus dibayarkan (Sembiring, 1986). Oleh sebab itu pendapatan perusahaan dari pembayaran premi harus disimpan sebagai cadangan benefit untuk membayar manfaat kepada peserta.

Penelitian mengenai premi tahunan tidak konstan dilakukan oleh Damayanti (2018) menentukan premi tahunan tidak konstan dan cadangan benefit. Penelitian tersebut menunjukkan bahwa nilai premi tahunan tidak konstan akan berubah tiap tahun dan cadangan benefit akan terus meningkat selama masih ada pembayaran premi. Sedangkan penelitian mengenai asuransi last survivor dilakukan oleh Nurfitri (2019) menentukan premi tahunan konstan dan cadangan benefit menunjukkan bahwa nilai premi tahunan konstan akan berbeda berdasarkan usia masuk peserta dan cadangan benefit akan terus meningkat setiap tahun selama pembayaran premi dilakukan

Pada penelitian ini penulis menghitung dan menentukan nilai premi tahunan tidak konstan asuransi last survivor dwiguna serta cadangan benefit dengan metode prospektif.

• 2.    Menghitung nilai premi tahunan asuransi last survivor dwiguna.

Pada langkah ini dilakukan perhitungan nilai premi tahunan konstan pada asuransi last survivor dwiguna yang bertujuan untuk mencari nilai a yang digunakan dalam menghitung premi tahunan tidak konstannya.

• 3.    Menentukan formula serta menghitung nilai premi tahunan tidak konstan pada asuransi last survivor dwiguna.

Sebelum menghitung nilai premi tahunan tidak konstan, diperlukan penurunan dan pembuatan formula premi tahunan tidak konstan. Setelah didapat formula premi tahunan tidak konstan, maka dicari nilai preminya dan melakukan perbandingan hasil dengan premi konstan.

• 4.    Menentukan formula serta menghitung nilai cadangan benefit premi  tahunan tidak

konstan pada asuransi  last survivor

dwiguna.

Sebelum menghitung nilai cadangan premi tahunan tidak konstan, diperlukan penurunan dan pembuatan formula cadangan premi tahunan tidak konstan. Setelah didapat formula cadangan premi tahunan tidak konstan, maka akan dicari nilai cadangan preminya.

• 3.    HASIL DAN PEMBAHASAN

  • 3.1    Penentuan Nilai Tabel Mortalitas

Pada tahap ini terlebih dahulu dilakukan penentuan nilai tabel mortalitas yang dicari untuk digunakan dalam perhitungan premi konstan maupun tidak konstan pada asuransi last survivor dwiguna. Nilai-nilai yang dicari antara lain: nilai  d _x = q_x I,,   d_y = q_y l_y,

^xy — Xyy ^{- l}x+l,y+1 , ^dan Xyy = XχXy-(Futami 1994).

• 3.2    Penentuan Nilai Komutasi

Pada tahap ini dilakukan penentuan dan perhitungan nilai komutasi yang dicari setelah didapatkan nilai tabel mortalitas yang dicari. Adapun nilai-nilai komutasi yang akan dicari ialah: nilai  D— — v^x l_x,  XX— = D_x + D₊₊₁ +-----+

D_ω _ i, +_x — ^χ++1d_x, M_x — C_x + +₊₁ i + ••• + C_ω _ i, D = ^y(^x+y)ι         n =D +n     +

x^,xy   ²      ⅛y,         y xy   ^xy ⁺ xχ+l,y+l ⁺

^Dx+2,y+2 ⁺ •, Cχy ^— ^²      d_xy, M_x= ^— C_xy ⁺

^Cx+1,y+1 ^{+ C}x+2,y+2 ■■■ (Futami 1993).

3.3 Perhitungan Premi Tahunan Konstan

Setelah diperoleh nilai tabel mortalitas dan komutasi maka dihitung nilai premi tahunan konstan pada asuransi last survivor dwiguna dengan formula berikut:

=R ̅̅̅̅: ^^| , dengan A    =( ¾÷_n+ ⁽ M_x-M_x+n)₊

̅̅̅̅:n |             _̈̅̅̅̅      ,                           :n|

̅̅̅̅:|

Dy+n+ (My~M_y+n)   Dχ+n,y+n+(M_xy~M_x+n:   ⁾)

D_y                   D_xy)

=(Nχ~N_x+n + ^Ny~^Ny+n ̅̅̅̅:n|⁼( Dx +

_-

Nχy-N_χ+n,y+n

Dxy .

⁾

Nilai premi tahunan tidak konstan sangat dipengaruhi oleh nilai a positif maupun negatif, nilai a merupakan persentase nilai dari premi konstan. Dalam penelitian ini menggunakan nilai a 10%. Jika nilai a negatif maka akan menyebabkan nilai premi menurun tiap tahunnya, sebaliknya jika a bernilai positif maka akan meningkat tiap tahunnya. Dengan menggunakan software Microsoft Excell 2016 diperoleh nilai perbandingan premi konstan dengan tidak konstan pada tabel 1.

• 3.4    Formulasi dan Perhitungan Premi Tahunan Tidak Konstan

Sebelum menghitung nilai premi tahunan tidak konstan terlebih dulu ditentukan formula premi tahunan tidak konstan pada asuransi last survivor dwiguna. Selanjutnya formula tersebut diubah dalam bentuk komutasi guna mempermudah perhitungannya. Untuk mendapatkan rumus persamaan perhitungan premi tahunan tidak konstan asuransi last survivor dwiguna maka digunakan prinsip ekuivalensi dimana nilai tunai anuitas pendapatan premi tidak konstan sama dengan nilai tunai santunan seperti berikut:

Tabel 1. Perbandingan Premi Konstan dengan Premi Tidak Konstan

Tahun	Premi Konstan	Premi Tidak Konstan
		Premi Menurun (a= -0.01724)	Premi Meningkat (= 0.01724)
1	0.1724	0.2052	0.1396
2	0.1724	0.1880	0.1568
3	0.1724	0.1707	0.1741
4	0.1724	0.1535	0.1913
5	0.1724	0.1362	0.2086
Jumlah	0.8620	0.8536	0.8704

Sumber: Data diolah, 2019

∑

tv

t=o

tP

̅̅̅̅

=  .A

̅̅̅̅:n|

P^rTK ̈     =R.AXVd

̅̅̅̅:n |            .    ̅̅̅̅:n|

_-

a

∑

tv'

I=O

tP

̅̅̅̅

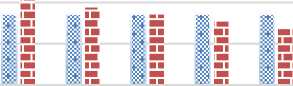
Apabila Tabel 1 disajikan dalam bentuk grafik, untuk pembayaran premi konstan dan premi yang menurun dapat dilihat pada Gambar 1.

⁼

∑

tv^t

t=0

̈

̅̅̅̅:n^|

^^^^^^~

̅̅̅̅

Pembayaran Premi Konstan dan Premi Turun

0.3

Formula premi tahunan tidak konstan yang telah diubah dalam bentuk komutasi

S

R.A

⁼

̅̅̅̅:n|

^∑

tv^t

tP̅̅̅̅

0

0.2

0.1

12345 Tahun

̈_̅̅̅̅

̅̅̅̅:   |

, dengan

B Premi Konstan ■ Premi Turun

.         Dχ+n+(M_x-M_x+n)   Dy+n+ ⁽M_y~M_y+n⁾

̅̅̅̅: n|⁼(        D_x         ⁺

D x+n,y+n+(M_xy~M_x+n:

D_xy) ,

∑

t=₀ ^tV'

t P ̅̅̅̅

Gambar 1. Premi Konstan (PK) dan Premi Turun (PT)

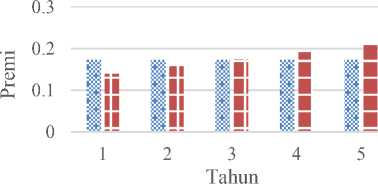
Sedangkan grafik untuk premi konstan dan premi meningkat dapat dilihat pada Gambar 2.

_∑n-1 t D

^∑t=0 ^{i u}xy+ t

D_xy

),

+

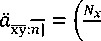
Nχy-N_χ+n,y+n

Dxy ,

Pembayaran Premi Konstan dan Premi Naik

Premi Konstan Premi Naik

Gambar 2. Premi Konstan (PK) dan Premi Naik (PN)

Pada pembayaran premi turun (PT), dari Gambar 1 terlihat bahwa

PT tahun ke - 5 < PK < PT tahun ke - 1 Mulai di tahun ke-5 peserta asuransi last survivor dwiguna akan membayar premi yang lebih kecil daripada peserta dengan jenis pembayaran  premi  konstan. Hal  yang

sebaliknya berlaku untuk pembayaran premi meningkat, dimana

PN tahun ke - 1 < PK < PN tahun ke - 5

Ditahun ke-5 untuk pembayaran premi meningkat peserta asuransi last survivor dwiguna akan membayar premi yang lebih besar daripada peserta dengan jenis pembayaran premi konstan.

• 3.5    Penentuan dan Perhitungan Cadangan
  
  Benefit

Berdasarkan premi tidak konstan, maka cadangan benefit a positif untuk awal tahun adalah

l^-^---∣ = ^r, A--1_ly-1-ι-1∣ ^- [(^⅛ + ^a^ ^•x+l,y+l:n-l| ^{+ a} ∑ L_l^sv^s sPWfl]

Cadangan benefit a positif untuk tahun kedua dan ketiga

2^-^-:-\ = ^r, ^ --2,y-1-ι~2∖ ^{- [(}^^RTK ^{+ 2 a} )^, ⅛-i ,_y-i_: i -1 | +

^a ∑_sζ_l^svs sPx₊2,y₊2 j

3^VXy--| = R- ^X + 3 ,y + 3-.-- 3∣ ^- [(⅛ ^{+ 3}^ )^, H_x y yy y 3--- ₃∣ ⁺

^a ∑^l=_l^sv" 3 P1-¾-+3 ]

Sehingga rumus umum untuk cadangan benefit a positif adalah

(Cy-H = ^R, ^x+t,y+t---t∣ ^{- [}(Ak ⁺ (t)^α ) - Sχ_tt,ytt---t∣ ⁺

V’ ^--t-1

^a ∑_s=l ^s3 s P---11-* ]

Sedangkan untuk negatif menjadi

^1-1-1 = R-^—y-l—i ^- [(⅛ ^- (0« ), O--1---1^--∣ ^-a ∑^-=_l^t ^C _sPx+ty+t^j

Nilai cadangan benefit dengan α negatif disajikan dalam tabel 2

Tabel 2. Cadangan Benefit a Negatif

Tahun ke-( t )	Cadangan benefit ( tV )
1	0.2151
2	0.4234
3	0.6238
4	0.8162
5	1

Sumber: Data diolah, 2019

Nilai cadangan benefit dengan α positif disajikan dalam tabel 3

Tabel 3. Cadangan Benefit a Positif

Tahun ke-( t )	Cadangan benefit ( tV )
1	0.1465
2	0.3183
3	0.5172
4	0.7438
5	1

Sumber: Data diolah, 2019

• 4.    KESIMPULAN DAN SARAN

  • 4.1    Kesimpulan

Nilai premi tahunan tidak konstan dengan nilai a positif pada tahun pertama sampai tahun kedua lebih kecil dari nilai premi tahunan tidak konstan dengan nilai a negatif. Perubahan terjadi ketika pada tahun ketiga sampai kelima dimana nilai premi tahunan tidak konstan dengan nilai a positif pada tahun ketiga sampai tahun kelima lebih besar dari nilai premi tahunan tidak konstan dengan nilai a negatif. Sedangkan perbandingan nilai premi tahunan tidak konstan dengan nilai premi tahunan konstan. Pada tahun pertama sampai kelima untuk nilai premi tahunan konstan akan tetap sama, untuk premi tahunan tidak konstan dengan nilai a positif dari tahun pertama hingga kelima terus meningkat, pada premi tahunan tidak konstan dengan nilai a negatif

dari tahun pertama hingga kelima akan terus menurun.

Cadangan benefit premi tidak konstan terbagi dua yang dipengaruhi nilai a positif dan negatif (cadangan dengan a negatif dan positif). Cadangan benefit terus meningkat setiap tahun untuk a negatif maupun positif selama masih ada pembayaran premi setiap tahun.

• 4.2    Saran

Pada penelitian ini penulis menentukan dan menghitung nilai premi tahunan tidak konstan pada asuransi last survivor dwiguna untuk dua orang tertanggung (peserta asuransi) serta menghitung cadangan benefit dengan metode prospektif. Untuk penelitian selanjutnya dapat menggunakan asuransi last survivor berjangka atau murni dengan premi tidak konstan serta menggunakan metode perhitungan retrospektif.

DAFTAR PUSTAKA

Damayanti, T.,  2018. Penentuan Premi

Tahunan Tidak Konstan dan Cadangan Benefit pada Asuransi Joint Life, Bogor: Institut Pertanian Bogor.

Futami, T., 1993. Matematika Asuransi Jiwa Bagian I. Terjemahan dari : Seime Hoken Sugaku Gekan ed. Jakarta: Oriental Life Insurance Culture Developement Center.

Futami, T., 1994. Matematika Asuransi Jiwa Bagian II. Terjemahan dari: Seime Hoken Sugaku Gekan ed. Jakarta: Oriental Life Insurance Cultural Developement Center.

Nurfitri, H., 2019. Penentuan Premi Tahunan dan Cadangan Benefit pada Asuransi Last Survivor, Bogor: Institut Pertanian Bogor.

Sembiring, R.,  1986. Buku Materi Pokok

Asuransi I. Jakarta (ID): Karunia.

108