EXISTENCE, UNIQUENESS AND STABILITY SOLUTIONS FOR NEW NONLINEAR SYSTEM OF INTEGRO-DIFFERENTIAL EQUATIONS OF VOLTERRA TYPE

E-Jurnal Matematika Vol. 9(2), Mei 2020, pp. 109-116

DOI: https://doi.org/10.24843/MTK.2020.v09.i02.p287

ISSN: 2303-1751

EXISTENCE, UNIQUENESS AND STABILITY SOLUTIONS FOR NEW NONLINEAR SYSTEM OF INTEGRO-DIFFERENTIAL EQUATIONS OF VOLTERRA TYPE

Faraj Y. Ishak

Department of statistics, Collage of Administration & Economics, University of Duhok, Iraq [email protected]

ABSTRACT

In this article, we established the existence, uniqueness and stability solutions for a nonlinear system of integro-differential equations of Volterra type in Banach spaces. Krasnoselskii Fixed point theorems and Picard approximation method are the main tool used here to establish the existence and uniqueness results.

Keywords: Existence and uniqueness, Picard approximation, Integrodifferential equations, Krasnoselskii fixed point theorem.

1. INTRODUCTION

The integral equations form an important part of applied mathematics, with links with many theoretical fields, especially with practical fields (K. E. Atkinson, 1997; P. Linz, 1985 ; E. Babolian and J. Biazar, 2000 ) The Volterra integral equations were introduced by Vito Volterra and then studied by Traian Lalescu in his 1908 thesis. Volterra integral equations find application in demography, the study of Viscoelastic materials, and in insurance mathematics through the renewal equation. Fredholm equations arise naturally in the theory of signal processing, most notably as the famous spectral concentration problem popularized by David Slepian. They also commonly arise in linear forward modelling and inverse problems. Throughout the last decade, physicists and mathematicians have paid attention to the concept of fractional calculus. Actually, real problems in scientific fields such as groundwater problems, physics, mechanics, chemistry, and biology are described by partial differential equations or integral equations. Many scholars have shown with great success the applications of fractional calculus to groundwater pollution and groundwater flow problems, acoustic wave problems, and others (F. Mainardi, 1997; P. Zhuang, F. Liu, V. Anh, and I. Turner, 2009; S.

B. Yuste and L. Acedo, 2005; C.-M. Chen, F. Liu, I. Turner, and V. Anh, 2007).

The Picard iteration method, or the successive approximations method, is a direct and convenient technique for the resolution of differential equations. This method solves any problem by finding successive approximations to the solution by starting with the zeroth approximation. The symbolic computation applied to the Picard iteration is considered in (Parker, G.E. and Sochacki, J.S. 1996; Bailey, P.B., Shampine, L.F. and Waltman, P.E. 1968) and the Picard iteration can be used to generate the Taylor series solution for an ordinary differential equation (Butris, R. N. 1994; Butris R.N., 2015; Butris, R. N. and Ghada, Sh. J. 2006) studied existence and unique solution for different kind of equations and (Raad N. Butris and Hojeen M. Haji 2019) studied existence and unique solution of Volltera-friedholm:

^ = A x + f (t, ε, ^rR{t - τ((x(τ) -y⁽0) ττ

In this work our aim is to show the existence solutions of the system of integrodifferential equations:

^ = A x( t) + ∫^t _aK (t, s)F( t, s, x(s),y(s))d s J = By t)) + ∫. _aG( t, s)H( t, s, x(s),y(s))ds (1)

Where ∈  ⊆ and ∈   ⊆

, and are closed and bounded, ∈  , let

( , , (), ()),  ( , , (), ()) is defined

on the domain:

( ⅛

Q₂M₂S₂T

A₂

Q₁M₁S₁T

Q₂M₂S₂T

⁾

less than one i.e.

_∗={( , ,  ,  )  [0,  ] x [0, ]x x }

(2)

(Ʌ )

_{+     <1}

λ_i A₂

(9)

Assume that the vector functions

( , ,  (),  ()),  ( , ,  (),  ()), and

kernels ( , ),  ( , ) are satisfying the

following inequalities:

‖ ( , ,  (),  ())‖≤,

‖  ( , ,  (),())‖

≤(3)

‖  ( , ,   ,   )-   ( , ,   ,)‖

≤   (‖  -‖

+‖  -  ‖(4)

‖   ( , ,   ,   )-   ( , ,   ,)‖

≤   (‖   -‖

+‖  -  ‖(5)

‖  ( , )‖≤        ^{(   )},‖  ( , )‖

≤        ^{(   )}(6)

‖   (    )‖ _{≤       ,}‖    ()

(7)

Where

,     ,      ,      ,     ,     ,     ,     ,     , are

positive constants

,    ∈       ,    ∈

,    [0,  ]      and ‖ ․‖=max ∈[ , ] |.|,

suppose that A = ( ), =( ) are nonnegative square matrices of order (n), we defined non empty sets as:

Define a sequence of functions

{    ( ,   )}       ,{   ( ,   )} as:

( ,  )=

+

∫₀^t ∫^t-_m^e^^t~)^(t, s)({t, s, m_m(s), m_m(s))dsds . (10)

( ^,   )⁼

+

∫  ∫      ^{(   )}  ( , )  ( , ,    (),   ())

With (0)=       , (0)=       ,

m=0,1,2…

=

=

Q₁M₁S₁T Λι

Q₂M₂S₂T ⅛

(8)

Where ∈   ⊆   ,,  ∈   ⊆   ,  ∈

,   ,   ,   ,   ,   , are positive constants

As well as, we suppose the maximum value of the following matrix:

2. PRELIMINARIES

Definition 2.1 (Syed Abbas, 2011 ). Assume that   ( , ) is defined on the set ( , )x ,

, ( , ) is said to satisfy Lipschitz condition with respect to the second variable, if for all ∈( , ) and for any ,

|  ( ,   )-  ( ,   )|≤  |   -|

where > 0 does not depend on ∈( ,)

Theorem 2.1: (Ascoli-Arzela theorem). Let /2 be a compact Hausdorff metric space. Then ⊂ C(Λ) is relatively compact if and only if M is uniformly bounded and uniformly equicontinuous.

Theorem 2.2: (Krasnoselskii fixed point theorem). Let M be a closed convex and nonempty subset of a Banach space X. Let A, B be the operators such that (i) Ax + By ∈ M whenever x, y ∈ M (ii) A is compact and continuous (iii) B is a contraction mapping. Then there exists z ∈ M such that z = Az + Bz.

Theorem 2.3 : (Raad N. Butri , Hewa S. Fari , 2015). Let { } be a sequence of real value function on the set E then { } is uniformly convergent on E if and only if given ∈>0 then there exist        such that :

|  ()-  ( )|< ∈    ( ,  ≥  , Е)

Theorem 2.4: (Banach's Fixed Point theorem). Let (X,d) be a complete metric space and let T: X→X be a contraction mapping. Then T has a unique fixed-point x∗ and for any x∈X the sequence {T ⁿ(x)}n-l converges to x∗.

Theorem 2.5: (Azhar H.Sallo , 2006 ). If the function f(X,y) satisfy the existence and uniqueness theorem for IVP(1), then the successive approximation Xn (X) converges to the unique solution y(X) of the IVP(1):

S=(X,y) ,y(⅞)=yo IVP (1)

3. MAIN RESULTS: EXISTENCE

Theorem 3.1: Let the right side of system (1) are defined and continuous on domain (2). Suppose that the vector functions F(t,s,X(t), y(t)) , H(t,s,X(t), y(t)) are satisfying the inequalities (3)-(5) and the conditions (6)-(9).Then there exist a sequences of functions (10) converges uniformly as m → ∞ on domain (2) to the limit functions which satisfying the following integral equations:

x(t, Xo)=

x_oe^At +

∫ ; ∫-^t∞^eA( t-s ⁾K(t,S)F(t,s,X(S), y(S))dsds

y(t^, X₀)=

y₀e^βt +

∫ ; ∫-∞ ^eB( t-s ⁾G(t,S)H(t,s,X(S), y(s))dsds

Provided that:

‖ χ∞ (t, X₀)-X₀‖≤

‖ y∞ (t, X₀)-yo‖≤Q₂M₂ S₂T

‖ Xm+1 (i, X₀)-Xm (i, X₀)‖     m ₍ ,

(_‖ Vm+l ⁽t, yo)-y_m ⁽t, yo_)‖)≤Ʌ⁰⁽

Ʌ0) ¹^O

for all m≥1 ,t∈ R¹

Proof:

By using the sequence of function (10) when m=0, we get:

‖ Xi (t, Xo)-Xo ‖=‖x_oe^At +

∫ ; ∫ ¹^^a( t-s ⁾K(t,S)F(t,s, Xo (s), yo (S))dsds ^-x_oe^At ‖

≤ ∫  ∫‖e^A( t-s ⁾K(t,s)F(t,s, ^xO (S), Vo (s))dsds ‖

0  -∞

≤ Q₁M₁δ₁ ∫ ; ∫ -∞ e   ⁽ t-s ⁾ dsds

≤ Q₁M₁S₁T ≤

And by the same we have

‖ yi (t, yo)-yo‖≤Q2^M2$2^T ^2

That is:

Xi (t, Xo ) t D y₁ (t, yo ) eD₁, for all te [0, T], Xq € Dp, yo ^{∈ D}H

Suppose that

Xp (t, ^xO )e D^, Fp (t, yo ) e D₁ for each

Xq E Dp , yo^e f)_{h ,} peZ⁺ , t∈ [0, T], by mathematical induction we conclude that:

^xm (t, ^xO )e D^, Vm (t, yo ) e D₁ for each

Xq E Dp , Vo ^e D_h ,m = 0,1,2,… ,

t∈ [0, T]

To prove that the sequences (10) convergence uniformly in domain (2):

‖ ^X2 (t, ^xO)-^χι (t, ^xO)‖ =

‖ x_oe^At +

∫ _∫ \e^A ₍ t-s ⁾K(t,S)F(t,s, ^xι (s), yi ₍S))dsds ^-x_oe^At ∫ ∫ ^l-^^A( t-s ⁾K(t,S)F(t,s, X₀ (s), y₀ (S))dsds ‖

≤

∫ ∫ -O=M⁽ t-s ⁾K(t,s)‖F(t,s, ^xI (S), yi (S)) -

F(t,S, ^xO (S), yo (S))‖dsds

≤ Q₁L₁δ₁ ∫ ; ∫ -∞ £  ⁽ t-s)_‖ ^i ^- ⅞ ‖+

‖ yi - yo ‖ dsds

≤ Q₁L₁S₁t (‖^xI ^{- x}O‖+‖Vi ^- yo ‖)

And by the same

‖ Vi (t, yo)-Vi (t, yo)‖

Q₂L₂δ₂t

≤         (‖^xι ^{- χ}o ‖

^2

+‖Vl ^- yo ‖)

By the mathematical induction the following inequalities hold:

‖ ⅛+l (t, ^xO)-^χ_m (t, ^xO)‖≤

(‖^χ_m ^- Xm-I‖+‖y_m ^- Vm-1 ‖) Ai

^‖y_m+ι ⁽t, yo)-y_m ⁽t, yo)‖≤

(‖Xm ^- Xm-I‖+‖y_m ^- Vm-1 ‖)

(12)

Rewrite (12) with vector form:

‖^xm+l(t, X₀)-Xm (t, X₀)‖

(_‖ Ym+l(t, y₀)-y_m (t, y₀)‖^)≤

lim∑Ʌ¹O ⅛o =∑Ʌ¹O ⅛o m→ ∞

I=I            I=I

=(I -Ʌ0) Vo

(16)

Thus the limiting relation (16) signifies uniform convergence of sequences:

^{^m (t, Xo)}m-0 ,{Vm (t, yo)}m=0 , that is:

lim Xm (t, ^xO )

m→ ∞

=⁽t, X₀) ,and lim y_m (t, yo)=y(t, yo ) m→ ∞

By all conditions and inequalities of the theorem the estimate

/QiLiSit

I QzL₂S₂I

∖ A₂

Q₁L₁S₁t∖

(

QzLz^zt j \

A₂ /

‖ Xm - Xm-I ‖ ^‖ Ym ^- Vm-I ^‖

That is:

Φm+1 (t, X₀ , yo)≤ Ʌ(t) Ψm (t, Xo , yo)  (13)

‖ ⅛+l (t, Xo)-^xm (t, X₀)‖     m _{( 1}

(_‖ ym+l ⁽t, yo)-y_m ⁽t, yo)‖^)≤Ʌ0(

Ʌ0) Vθ

Is hold for all m = 0,1,2, …

Where:

Ʌ(t)=

( QγLγδγt QγLγδγt \

^ y „ \

^⎜ Q₂L₂δ₂t Q₂L₂δ₂t ^⎟

⎝  ⅛     λ₂ ⎠

‖ Xm+1 (t, Xo)-Xm (t, Xo)‖

^, Ψ_m+1=(_‖Vm+1 ⁽t, yo)-y_m ⁽t, yo)‖⁾

‖ Xm (t, Xo)-Xm-I (t, Xo)‖ Φm=(_‖Vm (t, yo)-Vm-I (t, yo)‖

Take the maximum value for both sides of (13):

Φ _m+ι ≤ Ʌ 0 Φm              (14)

where

Ʌ0 =maxte[0,T] ^Ʌ (t)

By repletion of (14) we obtain:

Φ_m+1 ≤ Ʌ ¹O ^fPo

/QιM₁δ₁T∖

φ₀≤(Q2M2S2i^, ) , ∑ i^ι ^tPi ≤∑  ^ɅO^O

(15)

Since the matrix ɅQ has eigenvalue Aj =0,

⅛ ⁼     (Ʌ O)

_ Q₁M₁S₁T + Q₂M₂S₂T

^{=      +}

<1 ,

To prove that X⁽t, ^xO ) eD and y(t, Vo ) eD₁ we prove that:

lim m→ ∞( x_oe^At +

∫ ; ∫^t__me^A( t-s ⁾K(t,S)P(t,S, ^xm (S), y_m (s))dsds)= x_oe^At +

∫ ∫-∞   ⁽ t-s ⁾K(t,S)F(t,s,X⁽S), y(s))dsds

(17)

lim m→ ∞( y₀e^βt +

∫ ; ∫ -∞ £ ⁽ t-s ⁾G(t,S)H(t,s, ^xm (S), y_m (s))dsds)= Voe^et +

∫ , ∫-∞ ^eB( t-s ⁾G(t,s)H(t,s,X⁽S), y(s))dsds

(18)

We have:

‖ x_oe^At +

∫ J ∫I₀₀S^a( t-s ⁾K(t,S)F(t,s, ^χm (s), y_m (s))dsds ^-x_oe^At -

∫ ; ∫-∞ e ⁽ t-s ⁾K(t,S)F(t,s,X⁽S), y(s))dsds ‖

(19)

≤

∫ ; ∫ -∞ £ ⁽ t-s ⁾K⁽t,S)‖F(t,s, ^χ_m ⁽s), y_m ⁽s))-

F(t,s,X⁽S), y(S))‖dsds

≤ Q₁L₁S₁T (‖X_m -x^‖+^‖y_m -y ‖)

the series (15) is uniformly convergent, i.e.

And for the function y(t, Vo ) we have

∣∣y₀e^st +

∫o ∫- ∞ ^e^^ct ^^s)^c( t, s)H( t,s, x_m()) , y_m(s)) ds ds -y_oe^Bt —

∫o∫- ∞ ^{eSC t}~^{s) cc t}<s)H( t, s, x GO,y G0)dsds∣∣ ≤ Q2L2δ₂T d∣χ^ - χ U + ∣∣y_nt - _y ∣∣)

( Ik ^c t,Xo)-%^c t,xo)h

VIy^c t,yo) -y^c t,yo)∣∕ ^-

∕ ∣^χc 0^-%^c OIh

^Ao (Iyct)-yC t)∣)                 ⁽²⁰⁾

From (19) and condition (9) we have A™ → 0 when

m → ∞ that is:

And since the sequences:

{x_mct, Xo)}∞=o ,{y_mct,yo))m-0 uniformly

convergence to x c t, x_o), y c t, y_o) respectively on the interval [0,T], that is (17) ,(18) satisfies.

x ^c t, xo) = %^c t, xo) and y ^c t, yo) = y^c t, yo)

Therefor c ,   ), c ,   ) is a unique solution

for system (1).

Uniqueness

Stability

Theorem (3.2): If all conditions and assumptions of theorem (1.1) satisfied, then the functions c ,   ), c ,   ) are unique solution

for system (1) on domain (2).

Theorem (3.3): Under the hypothesis and conditions of theorem (11) if % c t, x_o), yc t, y_o) are any other solution of system (1) ,then the solution are stable if satisfies the inequality:

Proof: let

(x ^c t, %o) V yc t,yo)

(x_oe^At + ∫∫_m e^{ACt s)}KCt, s)F(t, s,x(s, ,y(s)^)dsW^he^re: Voe^{s t} + ∫∫l∞ e^C(t~^sCc(t, s)H(t, s,^c(s),^c(s))dsds )

be another solution for system (1) then:

∣x C t,%o) -%C t,%o)∣ ≤

∫o ∫-∞k^1ft“^s)KC t, s)[F(t, s, xCs),yGO) -F ( t, s, %Cs), yCs))]dsds∣∣

(Ik C t,%o) -%c t,%o)∣∖   ( ∈1∖

VIy^c t,yo) -y^c t,yo)^|/ “ W

x C t,%o) = x_oe^At +

∫₀^t ∫- ∞ e^{AC t s})KC t,s)F( t, s, xG0,yG0) ds ds y^c t,yo) = yoe^st +

∫ ∫₀₀ e^sct ^ ^s)CC t, s)H( t, s, xCs),yCs)) ds ds

Proof:

≤^Q⅞^t∣%-%| + |y-y|)

And

IkC t,xo) -xC t,xo)∣ ≤^q^C∣x -x I + ∣y-y∣)  (21)

∣y^c t,yo) -y^c t,yo)∣ ≤

∫0 ∫-∞ ∣e^{sc t} ^^s)cc t, s) [H( t, s, xG), y G)) -H ( t, s, %Cs),yCs))]ds ds ∣

≤^Q⅛^tk-%| + |y-y|)

Rewrite in vector form:

(Ik ^c t,xo)-%^c t,xo )∣∣∖

V∣y^ct,yo) -y^c t,yo)∣∕ ^

∣^{xc t)-xC t})ħ ^t)(∣yC t)-yC t)∣)

∣yC t,yo)-yC t,yo)∣≤^C∣x -χ∣ + ∣y-y∣) (22)

Rewrite (21), (22) in victor form we get:

(IkC t,xo) -%c t,xo)∣h

V ∣y^c t,yo) -y^c t,yo)∣∕

<Λ(_t√ ∣xC^t)^-^C^t)∣) ^{c t})(∣yC t)-yC t)∣)

By condition (9) and for e₁, e ₂ ≥ 0 we have:

By take the maximum value for both sides of (19) and reputation it we get:

(Ik ^c t,xo) - %^c t,xo)lh   (f∩

V∣y^c t,yo) -y^c t,yo)∣∕ ^- W

(23)

By the definition of stability, we find that

̅ (t, ^xO), ̅(t, yo ) is stable solution for system

(1)

Krasnoselskii theorem

≤

Q₁L_fiS₁T λι

‖X^-y‖

Thus using (25) we conclude that Ω is a contraction mapping.

Theorem (3.4): Suppose that the vector functions F(t,s,X(t), y(t)) , H(t,s,X(t), y(t)) in system (1) are satisfying the inequalities (6), (7)) ,and let Fi (t,s,X)≤Ni , F₂ (t,s,y)≤ N₂ ‖x_oe^At‖≤

^cI ,for all (t,s,X,y)e [0, T] x [0, T] xD^x F>ι ,T hen system (1.1) has at least one solution in [0, T] provided:

For X∈Ѱ calculating the norm of the function

F =Ω +Ω2 we have:

moreover for y∈Ѱ we obtain:

‖(Ω ∑y)(t)‖ t t

≤∫∫e^A( t-s ⁾K(t,s)‖F₂ (t,s,y(s))‖dsds

o -∞

_ QiN₂S₁T

≤≤r

ci ₊ TQiSi⁽ N_i+N₂)_≤r λl

QiL_fiS₁T<1

(24)

(25)

Proof: consider Ѱ={X ∈ C([0, T], R):|x|≤ r} denote the collection of all bounded and continuous function from [0, T] to R.

Assume that our function F(t,s,x,y ) in system (1) can be written as the sum of tow functions of the following form:

F(t,s,X,y)=Fi (t,S,x)+F₂ (t,s,y)

Where Fi , ^2 are Lipschitz continuous functions with Lipschitz constant Ffi , Ff2 .Define two operators on Ѱ as:

(Ωι^x)(t)=

x_oe^At +

∫ ∫-OO    ⁽ t-s ⁾K(t,S) Fi (t,S,X(S))dsds

(Ω^{( ,})(t _{) =}, ,  ( )

∫ ; ∫-^t∞ ^e^⁽ t-s ⁾K(t,S) F₂ (t,s,y(X))dsds

‖(ΩI^x)(t)+(Ω₂y)(t)‖≤‖x_oe^At‖+

∫ ; ∫-∞^{e   (} t-s ⁾K(t,S)‖Fi (t,s,X(S))+

F₂ (t,s,y(s) )‖dsds

≤ ci +     ⁽ _N1+N2)₌r

Thus for any X,y ∈Ѱ ,(ΩI^x)+(Ω₂y)∈Ѱ.

‖(Ω1^X)(t)-(Ωiy)(t)‖ t t

≤∫∫e^A( t-s ⁾K(t,s)‖Fi (t,s,X(S))

0 -∞

- Fi (t,s,y(S))‖dsds

≤ Qi^fi^i ‖x^-y‖∫ ; ∫-∞^{e   (} t-s ⁾ dsds

To prove the continuity of Ω2 ,let us consider a sequence y_n (t,S,y ) converging to y, and taking the norm:

‖(Ω2y_n)(t)+(Ω2y)(t)‖≤

∫ \ ∫-∞ e ⁽ t-s ⁾K(t,S)‖F₂ ⁽t,s, Vn (S))-F₂ (t,S,y(s))‖dsds

≤

QiF_f2S₁T

^‖ y∏

^-y‖

And hence whenever

y-n →y the function Ω₂y_n→Ω2y ,this prove the continuity of Ω2.

For compactness of Ω2 , let ti ≤ ^2 ≤T and taking the norm:

‖(Ω ∑y)(C₂)-(Ω∑y)(^l)‖≤

∫ J² ∫ -∞ ‖ e'¹⁽ t₂-S ⁾K(h,S) F₂ (h,s,y(s))‖dsds ^-

∫ ∫ -∞ ‖ e⁷¹⁽ t₁-s ⁾K(^i ,S) F₂ ⁽ti,S,y(s))‖dsds

2

^≤ <2₁¾ ∫∫

0 -∞

e ^λι ⁽t₂-s⁾ dsds

ti ti

^- Q₁N₂∫∫

e ^{11 (} t₁-s ⁾ dsds

≤

QiN₂S₁

o -∞

(12^- ^l )

The right-hand side of above expression does not depend on y, thus we conclude that Ω2 is relatively compact and hence Ω2 is compact by Arzela -Ascoli theorem. Using Krasnoselskii fixed point theorem we obtain that exist Z∈Ѱ such that:

Fz =   + F₂Z =

Which is a fixed point of F.

By the same steps we can prove that

Hz = H₁z + H₂ z = z

Hence system (1.1) has at least one solution in Ψ .

Example (3.1): consider the following system of integro-differential equations:

H = 0.988x(t) + ∫₂⅛≤ ^;' ^+o' d<

dy

dt

L33y(O + L^t₂

cos(t)+sin(s) x(s)-exp(y(s))

(26)

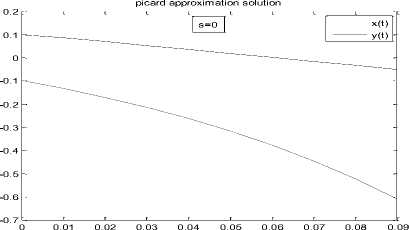
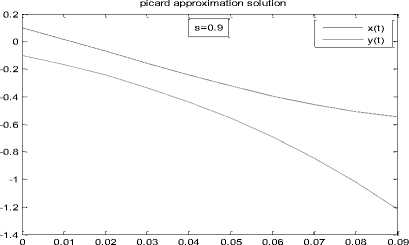
Figure (1)

4. CONCLUSIONS

For t,s ∈ I = [0,1] here x₀(t) = 0.1,y₀(t) = 0.1 , Tl _{1 xl}= 0.988 , B_{1x 1}= 1.33 , K(t,s) = ⅛≤ , (:.: ., ^o ' ^sγ   ,F(t,_s,x,y) =

^y⅛S⅞⅛>> ,H(t,s,x,y) = x(s)-exp(y(s)) _r, _ cos(x(s))

2          1 =    2      , ^ 2 =

φ ,H₁ = ^ ,H₂ = ^p    . Thus, by

Theorem (3.1), (3.4) the initial value problem (26) has a unique solution on [0,1], the numerical solution using MATLAB for Picard approximation method are show in figure (1):

	S = 0		s = 0.9
U	x(t∂	y H Ω	x ( t∕)	y ft)
0	0.1	-0.1	0.1	-0.1
0.01	0.0845	-0.1336	0.0160	-0.1667
0.02	0.0685	-0.1715	-0.070	-0.2443
0.03	0.0520	-0.2142	-0.1565	-0.3342
0.04	0.0351	-0.2623	0.2411	-0.4377
0.05	0.0178	-0.3164	-0.3216	-0.5563

Based on the results and discussion it can be concluded that: (1) The proof of existence solution for the non-linear system proposed in this paper using the existence and uniqueness theorem needs some hypotheses and conditions, (2). Using the idea of Krasnoselskii fixed point theorem was very effective for the proposed non-linear system of equations. The present work can be extended to boundary value problem.

ACKNOWLEDGEMENTS:

The author is grateful to the reviewers for their suggestions and advices.

REFERENCES

Bailey, P.B., Shampine, L.F. and Waltman, P.E. 1968 Nonlinear Two Point Boundary Value Problems. Academic, New York/London.

P. Linz, 1985 Analytical and Numerical Methods for Volterra Equations, SIAM, Philadelphia, Pa, USA.

Butris, R. N. 1994. "Existence of a solutions for a system of second order differential equations with boundary integral conditions", Iraq, Mosul, Educ. And Sci. J. Vol.18, pp.156-167.

Parker, G.E. and Sochacki, J.S. 1996 Implementing the Picard Iteration. Neural, Parallel and Scientific Computations,4, 97112.

K. E. Atkinson, 1997 The Numerical Solution of Integral Equations of the Second Kind, Cambridge University Press.

F. Mainardi, 1997 “Fractional calculus: some basic problems in continuum and statistical mechanics,” in Fractals and Fractional Calculus in Continuum Mechanics, vol. 378 of CISM Courses and Lectures, pp. 291–348, Springer, Vienna, Austria.

Azhar H.Sallo, 2006 .Existence and Uniqueness theorem for nonlinear fractional differential equation ,J.Edu,Sci,Vol(18), No(2).

E. Babolian and J. Biazar, 2000 “Solution of a system of non-linear Volterra integral equations of the second kind,” Far East Journal of Mathematical Sciences, vol. 2, no. 6, pp. 935–945.

S. B. Yuste and L. Acedo, 2005 “An explicit finite difference method and a new von Neumann-type stability analysis for fractional diffusion equations,” SIAM Journal on Numerical Analysis, vol. 42, no. 5, pp. 1862–1874.

Butris, R. N. and Ghada, Sh. J. 2006, The existence and approximation of periodic solution for systems of nonlinear integrodifferential equations of voltarra type, Iraq, Mosul, J. of Educ. And sci, Vol.18, No.2 104-114.

C.-M. Chen, F. Liu, I. Turner, and V. Anh, 2007 “A Fourier method for the fractional diffusion equation describing sub-diffusion, ”Journal of Computational Physics, vol. 227, no. 2, pp. 886–897.

P. Zhuang, F. Liu, V. Anh, and I.Turner, 2009 “Numerical methods for the variable-order fractional advection-diffusion equation with a nonlinear source term,” SIAM Journal on Numerical Analysis, vol. 47, pp. 1760–1781.

Syed Abbas, 2011 existence of solution to fractional order ordinary and delay differential equation and applications, Electronic Journal of Differential Equations, Vol. (2011), No. 09, pp. 1–11. ISSN: 1072-6691.

International Journal of Innovative Science, Engineering & Technology, Vol. 2 Issue 7.

Raad N. ButriS, Hewa S. FariS, 2015 Existence, Uniqueness  and Stability Solution of

Differential  Equations with Boundary

Conditions, IOSR Journal of Mathematics (IOSR-JM) e-ISSN: 2278-5728, p-ISSN: 2319-765X. Volume 11, Issue 6 Ver. III , PP 17-25.

Raad N. Butris and Hojeen M. Haji 2019 -Existence Uniqueness and stability solution of Volterra-Friedholm of integro-differntial equations - International Journal of Mechanical Engineering and Technology (IJMET)-Volume 10, Issue 07, July.

Butris R.N., 2015 Existence, Uniqueness and Stability Solution of Non-linear System of Integro-Differential Equation of Volterra type, University of Zahok, Iraq,

116