PENENTUAN PORTOFOLIO OPTIMAL SAHAM YANG TERGOLONG INDEKS LQ45 MENGGUNAKAN FUNGSI UTILITAS BENTUK PANGKAT
on
E-Jurnal Matematika Vol. 9(1), Januari 2020, pp.85-89
DOI: https://doi.org/10.24843/MTK.2020.v09.i01.p283
ISSN: 2303-1751
PENENTUAN PORTOFOLIO OPTIMAL SAHAM YANG TERGOLONG INDEKS LQ45 MENGGUNAKAN FUNGSI UTILITAS BENTUK PANGKAT
Kadek Intan Sari1§,Komang Dharmawan2, Luh Putu Ida Harini3
1Program Studi Matematika, FMIPA – Universitas Udayana [Email:intansari461@yahoo.co.id]
2Program Studi Matematika, FMIPA – Universitas Udayana [Email: k.dharmawan@unud.ac.id]
3Program Studi Matematika,, FMIPA – Universitas Udayana [Email: ballidah@unud.ac.id]
§Corresponding Author
ABSTRACT
The proportion of a portfolio can not eliminate risk as a whole but can reduce risk compared to investing in one type of security. One way to determine the optimal portfolio is to use the rank utility function. The purpose of this study is to determine the optimal portfolio of shares of PT. Adhi Karya (Persero) Tbk. (ADHI) and PT. XL Axiata Tbk. (EXCL) for the period January 2017-December 2018 by determining expected returns, variances, standard deviations, covariates, correlation coefficients between shares, and formulating the portfolio equation into a utility function with a rank of 0.5. This study produces a utility value (U (α)) of 0.996181 which means that the level of satisfaction with the proportion of shares of the portfolio is 99.618183%. This value is very high so the proportion of each share is well performed.
Keywords: Optimal Portfolios, Expected Returns, Utility Functions.
menghindari risiko juga untuk memaksimalkan return. Salah satu cara untuk membentuk suatu portofolio yang optimal adalah menggunakan model fungsi utilitas.
Menurut Husnan (1998), fungsi utilitas merupakan suatu model yang mendasari pemilihan portofolio dalam konteks mean-variance, dengan mean merupakan tingkat pengembalian (return) dan variance merupakan tingkat risiko (risk). Terdapat beberapa jenis utilitas yaitu fungsi utilitas linear, fungsi utilitas eksponensial, fungsi utilitas logaritma dan fungsi utilitas pangkat.
Penelitian terdahulu yang berhubungan dengan optimalisasi portofolio menggunakan fungsi utilitas yaitu: Devi, dkk (2013) memaparkan cara menganalisis portofolio saham LQ45 menggunakan fungsi utilitas kuadratik sangat dipengaruhi oleh expected return dan standar deviasi. Hal ini menunjukkan bahwa utilitas dari kenaikan portofolio akan meningkat dan akan menurun jika variansnya meningkat. Perubahahan yang relatif besar dipengaruhi oleh indeks risk averse. Portofolio optimal yang didapat menunjukkan bahwa faktor yang memengaruhi portofolio optimal
adalah keuntungan investasi bebas risiko, indeks risk aversion, dan suku bunga pinjaman.
Indeks LQ45 hanya terdiri dari 45 saham yang terpilih melalui berbagai kriteria pemilihan, sehingga akan terdiri dari saham-saham dengan likuiditas dan kapitalisasi pasar yang tinggi. Agar investor mendapatkan tingkat pengembalian (return) yang sesuai dengan harapan dengan risiko yang minimal. Investor harus dapat menentukan jenis saham yang mempunyai karakteristik searah dengan perubahan IHSG misalnya indeks saham LQ45. Karakteristik saham yang termasuk dalam kategori indeks LQ45, adalah saham-saham yang cenderung stabil karena saham-saham tersebut termasuk saham-saham yang mudah diperjual-belikan baik dalam kondisi pasar lemah maupun kuat, dengan mudahnya saham-saham LQ45 diperjual-belikan maka akan dapat menunjukkan suatu portofolio yang optimal.
Hal inilah yang menjadikan daya tarik penulis untuk melanjutkan penelitian menentukan portofolio optimal pada saham LQ45 dengan menggunakan fungsi utilitas bentuk pangkat dengan Studi Empiris pada dua saham LQ45 yaitu saham PT. Adhi Karya (Persero) Tbk. (ADHI) dan PT. XL Axiata Tbk. (EXCL) periode Januari 2017 – Desember 2018.
terdapat variasi tingkat keuntungan (kovarians) antarsekuritas pada suatu periode tertentu, sehingga dengan mengombinasikan berbagai sekuritas tersebut dalam suatu portofolio, tingkat keuntungan akan lebih stabil dan risikonya berkurang.
Sebagai ilustrasi, misalkanR 1 adalah tingkat keuntungan saham 1, dan R 2 adalah tingkat keuntungan saham 2, σp adalah varians dari portofolio, kemudian dan masing-masing adalah variansi dari saham pembentuk portofolio, dan adalah alokasi modal dan c0v RS1 ,S2 ) adalah kovarians antara tingkat keuntungan saham 1 dengan saham 2, maka variansi dari portofolio dirumuskan sebagai berikut
σp = α1σ1 + a2 σ2 + 2a1a2 covRS1 ,S2 ) dari persamaan tersebut, akan didapatkan bentuk umum perumusan varians yang
menyatakan nilai risiko investasi portofolio. m mm
^p
=∑
i=i
a fa? +
∑∑
aIOtjOij i ≠ j
i=ιj=i
dengan- j = c 0 v (Sl, S1)
Pembentukan sebuah portofolio tidak dapat menghilangkan risiko secara utuh, tetapi dapat mengurangi risiko dibandingkan dengan berinvestasi pada satu jenis sekuritas saja.
Menurut teori portofolio mean-variance, investor mengharapkan tingkat keuntungan tertentu dalam pembentukan portofolio. Bentuk umum dari tingkat keuntungan (return) dari
portofolio adalah T? p = a 1R1 + α2 R2 + —+
amRm atau secara sistematis dapat ditulis
dengan ai adalah i=1,2,…,m. Untuk
m
= ∑ °rR i i=i
alokasi modal saham ke menentukan nilai harapan
keuntungan (mean) dari portofolio, digunakan
persamaan berikut yang merupakan bentuk
umum dari E (Rp) = α1 ERR1 ) + a 2 ERR2 ) + —+ CCeE RRmy yaitu :
m
E RRp) = ∑aiERR ) i-i
dengan ERR) adalah rataan tingkat keuntungan saham ke-i. Selain mengharapkan tingkat keuntungan tertentu, investor juga
mengharapkan risiko seminimal mungkin. Penurunan risiko ini dapat dilakukan karena
Fungsi Utilitas Bentuk Pangkat
Fungsi utilitas pangkat memiliki bentuk (Fabozzi dan Pachamanova,2016):
URx) = xa,0 < a < 1
dengan x menyatakan jumlah modal atau harapan keuntungan dalam investasi dan a menyatatakan preferensi risiko dari investor terhadap fungsi utilitas bentuk pangkat. Nilai a memiliki kisaran 0 < a <1 . Hal ini
menandakan investor hanya diperbolehkan untuk mengambil preferensi risiko yang terbatas pada interval (0,1), nilai 0 dan 1 tidak diambil sebab akan memberikan nilai utilitas yang bersifat konstan, sehingga hal ini tidak sesuai dengan harapan investor yang bersifat risk averse.
2. METODE PENELITIAN
Jenis dan Sumber Data
Data yang digunakan dalam penelitian ini adalah data sekunder berupa harga penutupan dari saham PT. Adhi Karya (Persero) Tbk. (ADHI) dan PT. XL Axiata Tbk. (EXCL) periode Januari 2017-Desember 2018. Dalam penelitian ini penulis mengambil data yang
diperoleh dari http://www.finance.yahoo.com.
Metode Analisis Data
Adapun langkah-langkah yang dilakukan untuk menentukan portofolio optimal dari sahamPT. Adhi Karya (Persero) Tbk. (ADHI) dan PT. XL Axiata Tbk. (EXCL) periode Januari 2017-Desember 2018 yaitu :
1.
-
2.
-
3.
-
4.
-
5.
Menentukan return masing-masing saham dengan menggunakan persamaan Rt = ln θ^) dan menentukan nilai harapan pengembalian (expected return)dengan menggunakan persamaan E (R) = 1∑^ 1R t dengan R t adalah tingkat pengembalian saham, St adalah harga saham pada periode t, dan St - 1 adalah harga saham pada periode t-1.
Menentukan varians dengan menggunakan persamaan σ2 = ^^ 1(Rt — ERR))2 dan menentukan standar deviasi atau akar
kuadrat varians tiap saham. Menentukan nilai kovarian menggunakan persamaan
E [(X — E[X])(Y — E[Y])]
antar saham cov (X, Y) = dan nilai antarsaham
koefisien
korelasi
menggunakan persamaan
cov ( , )
p (X,Y)=-==^== √var(X)var (Y)
kemudian dilanjutkan dengan menentukan fungsi utilitas bentuk pangkat yang digunakan yaitu:
U (a') = a 1 /2
.
Merumuskan persamaan portofolio ke dalam fungsi utilitas bentuk pangkat dengan
A = E[α] = (r — r2)α + (1 + r2 ),
B = V ar[ a] = ( σ2+σ2 — 2 p σ1σ2 )a2 +(2pσ1σ2 — 2σ2i)a + σf ,
dan merumuskan ke persamaan portofolio
U,, (A') V ar (a)
6.
f (%) = U (4) +
f (%) =A p +
Mencari solusi menjabarkan
A r = (r
—
r2 ),
B, = 2(σ1 + 222 —2^2).
P(P-I)
2 Ap -2 B.
.
2
portofolio optimal dengan
— 2 ) + (2
dan merumuskan ke dalam persamaan portofolio untuk memperoleh portofolio optimal dengan persamaan:
(p — 1)(p — 2)
-
f, (a) = p A 2 A r + —-------A rB
-
+ pP-lAB, = 0.
2
Data historis harga penutupan (close price) bulanan saham PT. Adhi Karya (Persero) Tbk. (ADHI) dan PT. XL Axiata Tbk. (EXCL) periode Januari 2017–Desember 2018 disajikan pada Tabel 1.
Tabel 1. Close Price Saham ADHI dan EXCL
|
Tanggal |
Close Price (ADHI) |
Close Price (EXCL) |
|
2017-01-01 |
2100 |
2910 |
|
2017-02-01 |
2130 |
2990 |
|
2017-03-01 |
2370 |
3060 |
|
2017-04-01 |
2260 |
3210 |
|
2017-05-01 |
2350 |
2960 |
|
2017-06-01 |
2150 |
3410 |
|
2017-07-01 |
2220 |
3360 |
|
2017-08-01 |
2020 |
3600 |
|
2017-09-01 |
2000 |
3740 |
|
2017-10-01 |
2190 |
3380 |
|
2017-11-01 |
1955 |
3080 |
|
2017-12-01 |
1885 |
2960 |
|
2018-01-01 |
2230 |
2990 |
|
2018-02-01 |
2480 |
2950 |
|
2018-03-01 |
2070 |
2520 |
|
2018-04-01 |
1880 |
2120 |
|
2018-05-01 |
1945 |
2100 |
|
2018-06-01 |
1790 |
2520 |
|
2018-07-01 |
1605 |
2750 |
|
2018-08-01 |
1490 |
3180 |
|
2018-09-01 |
1390 |
2760 |
|
2018-10-01 |
1125 |
2620 |
|
2018-11-01 |
1565 |
2040 |
|
2018-12-01 |
1585 |
1980 |
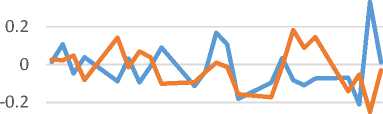
Setelah memperoleh data harga penutupan dilanjutkan dengan mengubah data dari harga penutupan saham menjadi tingkat pengembalian (return) yang ditunjukkan pada Gambar 1.
Plot Nilai Return Saham ADHI dan EXCL
0.4
-0.4
MiMBBHB Return ADHI ^^^M Return EXCL
Gambar 1. Plot Nilai Return Saham ADHI dan EXCL.
Gambar 1. menunjukkan bahwa return saham ADHI dan EXCL cenderung fluktuatif. Terlihat pula nilai return saham ADHI mengalami peningkatan pesat pada akhir periode, sedangkan return saham EXCL mencapai nilai terendah. Dengan menggunakan data nilai tingkat keuntungan (return) masing-masing saham, maka untuk selanjutnya akan dihitung nilai statistik deskriptif dari masing-masing return saham. Statistik deskriptif tersebut ditampilkan pada Tabel 2.
Tabel 2. Statistik Deskriptif Masing-masing Saham
|
Saham |
Return Saham ADHI |
Return Saham EXCL |
|
Expected Return |
-0,012232736 |
-0,01674 |
|
Max |
0,330102788 |
0,182322 |
|
Min |
-0,211520711 |
-0,25022 |
|
Simpangan Baku |
0,117581672 |
0,105075 |
|
Varians |
0,01382545 |
0,011041 |
Sumber: Data diolah (2019)
Tabel 3. Kovarians dan Korelasi Saham ADHI & EXCL
|
Kovarians ADHI dan EXCL |
-0,00335 |
|
Korelasi ADHI dan EXCL |
-0,27091 |
Sumber: data diolah (2019)
Tabel 3 menunjukkan korelasi kedua saham bernilai negatif. Ini berarti apabila salah satu saham mengalami peningkatan maka saham lainnya akan mengalami penurunan dan begitu pula sebaliknya.
Setelah semua nilai statistik deskriptif yang diperlukan berhasil diperoleh, seluruh nilai itu kemudian dinotasikan sebagai berikut.
7I = (ADHI) = -0,012232;
r2 = (EXCL) = -0,01674;
V1 = ADHI = 0,117582;
V2 = EXCL = 0,105075;
V? = Varians Return ADHI = 0,013825;
V2 = Varians Return EXCL = 0,011041;
p = Korelasi Return ADHI dan EXCL
= -0,27091.
Selanjutnya variabel-variabel tersebut
digunakan dalam menghitung portofolio optimal. Misalkan proporsi dana yang diinvestasikan pada saham ADHI =a1 = . Ini
berarti proporsi dana yang diinvestasikan pada saham EXCL = ¾ =1-a. Dengan demikian diperoleh:
A=(7ι - r2 )a+(1+r2 )
= 0,004508a + 0,983258
Ini berarti:
A′ = 0,004509.
Sedangkan
B=(Vi + V2 -2P V1V2)α2 +
Berdasarkan Tabel 2. terlihat bahwa nilai harapan keuntungan (expected return) untuk saham ADHI dan EXCL bernilai negatif yang berarti kedua nilai saham cenderung mengalami penurunan. Selain itu, nilai simpangan baku untuk return saham ADHI dan EXCL hampir sama besar. Ini berarti simpangan yang dialami kedua saham hampir sama.
Setelah memperoleh statistik deskriptif masing-masing return saham, dilanjutkan dengan menghitung nilai kovarians dan korelasi kedua return saham. Selanjutnya diperoleh nilai kovarians dan korelasi antarsaham yang perhitungannya diperoleh dengan bantuan Microsoft Excel dan disajikan sebagai berikut.
(2P v1v2 -2V2 )a+ v2 .
Ini berarti:
B = 0,063120a - 0,028775
Jika fungsi utilitas yang diberikan adalah
U(a)=a1/2 . Ini berarti
f(a)=AP +P(P -1)Ap~2B .
Berdasarkan syarat f'(a)=0, diperoleh:
f, (a)=pA2A, +
E(E-1)(E-2) 2
A'B +p( P-ι ) AB'.
2
-0.000008a2 - 0.00774606a
+0.005725 = 0
Solusi untuk a dan β diperoleh dengan pemfaktoran a = 0,738540 atau =
876,208330. Nilai yang dipilih adalah = 0,738540 karena berada pada rentang 0 hingga 1. Ini berarti proporsi dana yang optimal untuk saham ADHI adalah sebesar a1 = =
0,738540 = 73,854% dan untuk saham EXCL adalah sebesar «2 =1-a=1-0,738540= 0,261459 = 26,146.Ini berarti nilai ekspektasi portofolio adalah
A = 0,986587.
dan varians portofolio adalah
B = 0,0322914.
Selanjutnya nilai utilitas dapat dihitung sebagai:
f(a)=AP +P(P -1)AP-2B
= 0,992378
Sehingga
U(f(a))=(f(a))1/2
= (0,992378)1/2
= 0,996181.
Berdasarkan pembahasan diperoleh proporsi portofolio untuk saham ADHI sebesar 73,854% dan saham EXCL sebesar 26,146%. Ekspektasi portofolio bernilai 0,986587 dan varians portofolio bernilai 0,03229. Sedangkan nilai utilitasnya adalah sebesar 99,618183% yang berarti kepuasan terhadap portofolio sangat tinggi.
Saran
Penelitian selanjutnya bisa diuji coba pada berbagai saham dengan korelasi yang berlainan tanda (ada korelasi negatif dan korelasi positif) kemudian dibandingkan utilitasnya. Penelitian lanjutan juga dapat dilakukan dengan menggunakan tiga atau lebih saham dengan teknik pencarian solusi menggunakan pendekatan numerik yang sesuai.
DAFTAR PUSTAKA
Devi, Kadek Frisca Ayu, Dharmawan, Komang, dan Asih, Ni Made. 2013. Analisis Portofolio Saham LQ45 Menggunakan Fungsi Utilitas Kuadratik. e-Jurnal Matematika. Vol. 2. No. 1. Halaman 33-36.
Fabozzi, Frank J. dan Pachamanova, Dessislava A. 2016. Portfolio Construction and Analytics. John Wiley & Sons: New Jersey.
Husnan, Suad. 1998. Dasar-dasar Teori Portofolio dan Analisis Sekuritas. Edisi ketiga. UPP AMP YKPN. Yogyakarta.
Tandelilin, Eduardus. 2010. Portofolio dan Investasi. Edisi Pertama. Kanisius: Yogyakarta.
Yahoo Finance, [online]. Available :http://www.finance.yahoo.com/. Terakhir diakses tanggal 1 Mei 2018.
89
Discussion and feedback