E-Jurnal Matematika Vol. 9(1), Januari 2020, pp.79-84

DOI: https://doi.org/10.24843/MTK.2020.v09.i01.p282

ISSN: 2303-1751

PENERAPAN ALGORITMA GLOWWORM SWARM OPTIMIZATION PADA MODEL GEOGRAPHICALLY WEIGHTED REGRESSION DENGAN KERNEL ADAPTIF

I Gede Hardi Karmana1§, Luh Putu Ida Harini2, Ketut Jayanegara3,

I Putu Eka Nila Kencana4

1Program Studi Matematika – Universitas Udayana [Email: dkar.math@gmail.com]

2Program Studi Matematika – Universitas Udayana [Email: ballidah@unud.ac.id]

3Program Studi Matematika – Universitas Udayana [Email: ktjayanegara@unud.ac.id]

4Program Studi Matematika – Universitas Udayana [Email: i.putu.enk@unud.ac.id]

§Corresponding Author

ABSTRACT

This study aimed to apply glowworm swarm optimization (GSO) algorithm as an alternate way to obtain optimal bandwidth in geographically weighted regression (GWR) model with adaptive kernel function. The result showed that GSO was able to obtain optimal bandwidth with lower cross validation (CV) value than the traditional way that was using k-nearest neighbor (KNN) algorithm. Unfortunately, the running time of GSO was far slower than KNN was.

Keywords: geographically weighted regression (GWR), bandwidth, algorithm, k-nearest neighbor (KNN), glowworm swarm optimization (GSO)

  • 1.    PENDAHULUAN

Transportasi adalah suatu cara untuk berpindah dari satu lokasi ke lokasi lainnya. Seiring perubahan zaman, teknologi tranportasi juga semakin berkembang. Perkembangan ini memengaruhi hubungan manusia pada tiap daerah. Hal ini menyebabkan perubahan pada suatu daerah akan semakin mudah memengaruhi daerah lainnya. Kondisi tersebut kemudian dicoba untuk dijelaskan melalui model yang disebut geographically weighted regression (GWR).

GWR merupakan suatu model regresi dengan pembobot berdasarkan jarak geografis masing-masing wilayah. Pembobot diperoleh dengan mentransformasi jarak antar wilayah ke dalam suatu fungsi yang disebut fungsi kernel. Fungsi kernel pada GWR dibagi menjadi dua yaitu fungsi kernel tetap dan kernel adaptif (Caraka & Yasin, 2017).

Secara umum, perbedaan kedua fungsi kernel tersebut adalah fungsi kernel tetap menggunakan bandwidth yang sama untuk semua wilayah, sedangkan fungsi kernel adaptif bisa menggunakan bandwidth yang berbeda untuk tiap wilayah. Penentuan bandwidth yang optimal pada fungsi kernel adaptif cenderung lebih memakan waktu

daripada fungsi kernel tetap sehingga banyak aplikasi statistika memilih untuk menyederhanakan solusi dengan menggunakan algoritma k-nearest neighbor (KNN). Namun, penggunaan algoritma KNN justru menghilangkan sifat adaptif karena bandwidth disesuaikan berdasarkan jumah tetangga yang sama untuk seluruh daerah. Ini berarti diperlukan suatu algoritma yang mampu mempertahankan sifat adaptif tersebut. Salah satu algoritma tersebut adalah glowworm swarm optimization (GSO).

Glowworm swarm optimization (GSO) merupakan suatu algoritma optimasi yang berbasis swarm intelligence. Ini berarti GSO mencari solusi optimal dengan membangkitkan suatu gerombolan dan memanfaatkan informasi yang dimiliki masing-masing individu pada gerombolan tersebut (Krishnanand & Goshe, 2006).

Penelitian sebelumnya mengenai GWR dilakukan oleh Utari dkk (2019) menunjukkan bahwa GWR dengan fungsi kernel adaptif lebih bagus daripada GWR dengan fungsi kernel tetap maupun regresi linier berganda pada data dengan heterogenitas spasial. Penelitian sebelumnya mengenai GSO dilakukan oleh Krishnanand dan Ghose (2009)

menunjukkan bahwa GSO dapat dipakai untuk mencari titik-titik ekstrim lokal maupun global pada berbagai fungsi.

Berdasarkan penjabaran yang telah diberikan, penulis melakukan penelitian untuk mengaplikasikan GSO pada GWR dengan fungsi kernel adaptif.

  • 2.    METODE PENELITIAN

    • 2.1    Fungsi Kernel dan Bandwidth

Fungsi kernel merupakan suatu fungsi yang mentransformasikan nilai ke dalam rentang 0 hingga 1. Fungsi kernel pada GWR mentransformasikan nilai jarak antar daerah (amatan) menjadi nilai bobot. Jarak antar daerah dihitung dengan (Caraka & Yasin, 2017):

dij =√ (ui — Uj)2 + (v i — Vj}2       (1)

dengan:

d ij : jarak Euclidean antara daerah ke-i dengan daerah ke-j,

(u ,, v i) : letak geografis daerah ke-i, (Uj, v j) : letak geografis daerah ke-j.

Fungsi kernel yang dibagi menjadi fungsi kernel tetap dan fungsi kernel adaptif tergantung pada nilai bandwidth yang digunakan. Kernel tetap menggunakan bandwidth yang sama untuk seluruh daerah, sedangkan kernel adaptif dapat menggunakan nilai bandwidth yang bervariasi untuk tiap daerah. Selain itu, kernel dibagi pula menjadi beberapa bentuk fungsi. Salah satunya yang sering digunakan adalah fungsi kernel Gaussian. Nilai dari fungsi kernel adaptif Gaussian (w(u ,,v i)) dihitung dengan persamaan:

Wj (U i, v i) = e-(⅛)             (2)

dengan h t adalah bandwidth kernel Gaussian untuk daerah ke-i.

  • 2.2    Greographically Weighted Regression

Geographically Weighted Regression (GWR) adalah suatu metode statistika yang memodelkan suatu pengaruh variabel bebas pada variabel dengan melihat heterogenitas spasial antar daerah. Heterogenitas spasial adalah suatu kondisi saat pengaruh variabel bebas terhadap variabel terikat pada suatu daerah ternyata bervariasi dengan daerah lainnya. Model GWR ditulis sebagai berikut (Caraka & Yasin, 2017).

p

y i = OoUu i, V i) + ∑ βk(u i, v ^x iιk k=i

dengan:

+ Zi (3)


yt      : nilai variabel terikat amatan ke-i,

xi,k    : nilai variabel bebas ke-k amatan ke-i,

(u,, V1") : letak geografis daerah (amatan) ke-i, βo (u,, v) : nilai intercept amatan ke-i, βk (u t, v i) : nilai slope amatan ke-i,

εi      : nilai galat pada amatan ke-i yang

diasumsikan berdistribusi TV (0, σ2 ).

Estimasi parameter dari model GWR dapat dihitung sebagai berikut:

βU l, v) = (Xτ W (u l, V1W 1 Xτ W (u l, vl)Y  (4)

dengan:

β (U l, Vd =

'β0 (U t, vd'

■ 1

x1,1

...    x 1 , p

βl (Ui,vd

,X =

1

X2,1

...    X 2 , p

βp (Ui, vd.

1

x n, 1

.   Xn, p.

H7I

W (u i, v i) = I

( U i, v i)

0

. 0J

Wn (U l, v i)J

0

V2 (Ui,v i)   ...

0

0

matriks


■=B

Matriks  W(u,, v,) merupakan


pembobot amatan ke-i dan Wj(ui,vd merupakan nilai bobot amatan ke-i terhadap amatan ke-j. Matriks pembobot diperoleh melalui transformasi fungsi kernel.

Pada penentuan matriks pembobot GWR, nilai bandwidth yang digunakan merupakan nilai bandwidth yang menghasilkan pembobot yang paling optimal. Salah satu kriteria yang digunakan untuk menentukan apakah suatu bandwidth menghasilkan pembobot yang optimal adalah dengan menggunakan nilai Cross Validation (CV). Nilai CV dirumuskan sebagai:

n

CV= ∑(yi-y*i<hi))2 (5) i-i

dengan y^ (h) merupakan nilai estimasi variabel terikat untuk amatan ke-i tanpa menyertakan variabel bebas ke-i pada estimasi parameter modelnya. Bandwidth yang optimal adalah bandwidth yang menghasilkan nilai CV minimal (Caraka & Yasin, 2017).

  • 2.3    Koefisien Determinasi (R2 )

Koefisien determinasi merupakan suatu ukuran yang menyatakan seberapa besar variabel bebas dapat menjelaskan variabel terikat. Nilai koefisien determinasi yang semakin besar menandakan variabel-variabel bebas pada model semakin mampu menjelaskan variabel terikat. Koefisien

determinasi dirumuskan sebagai (Caraka & Yasin, 2017):

R2 = 1-∑⅛≡^(^-⅛^-          (6)

Z”= ι(yz - y)2

dengan yi menyatakan nilai dugaan variabel terikat untuk amatan ke-i dan y merupakan nilai rata-rata variabel terikat.

  • 2.4    Algoritma k-Nearest Neighbor

Algoritma k-nearest neighbor (KNN) adalah suatu algoritma yang termasuk metode machine learning. Ini berarti algoritma KNN dapat digunakan untuk mencari solusi optimal dari suatu himpunan data. Algoritma KNN digunakan untuk mengklasifikasikan data berdasarkan jarak terdekat ke-k dari suatu titik pada data (Sutton, 2012). Algoritma KNN dijabarkan pada Gambar 1.

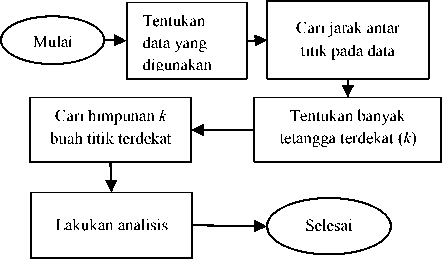
Gambar 1. Diagram Alir Algoritma KNN (Sumber: Sutton, 2012)

  • 2.5    Algoritma Glowworm Swarm

Optimization (GSO)

Glowworm Swarm Optimization (GSO) diperkenalkan oleh K.N. Krishnanand dan D. Ghose pada tahun 2005. Algoritma ini terbagi menjadi tiga bagian yaitu tahap pembaharuan luciferin, pergerakan, dan pembaharuan jangkauan ketetanggaan (Krishnanand & Goshe, 2006).

Tahap pembaharuan luciferin dirumuskan sebagai:

  • 11    (t) = (1 - p)l (f — l) + y.F (xi (t — 1))   (7)

dengan

: konstanta peluruhan luciferin, : konstanta peningkatan luciferin,

I i (t')       : jumlah luciferin iterasi ke-1,

I i ( t — 1) : jumlah luciferin iterasi ke-( t -1),

xi (t — 1) : posisi glowworm ke-i saat

iterasi ke-(t-1),

F (χ( t — 1)) : nilai fitness glowworm ke-i saat iterasi ke- (t-1).

Tahap pergerakan dirumuskan sebagai:

Xi(0 = x(t - 1) +

∕ Xj(t —1) —χi(t - 1) \           (8)

∖ IIxJ (t — 1)— xt(t — 1)H×

Dengan x(t) adalah posisi glowworm ke-i saat iterasi ke-1, X(tt — 1) adalah glowworm yang menjadi tujuan, s adalah ukuran langkah, dan Il || adalah jarak Euclidean. Pergerakan dilakukan setelah glowworm yang menjadi tujuan dipilih berdasarkan peluang:

, f λ            Ij(0 — it(0

'   (t)= ∑ ∈ ^t)(«0—MO)  (9)

dengan

( ): peluang glowworm ke-i memilih glowworm ke-j sebagai tujuan, Ni ( t) : Himpunan tetangga dari glowworm ke-i.

Ni ( t) didefinisikan sebagai:

NiCO = Vldi((0<^(0J f(0< Z(CO) dengan

( )  : jarak Euclidean antara glowworm

ke-i dan ke-j,

( )   : jangkauan ketetanggaan

glowworm ke-i.

Pembaharuan jangkauan ketetanggaan

dirumuskan sebagai:

Tg (t) = mm {rs,mafcs(0,rj(t — 1) + e(nt— lM(t)l)}    (10)

dengan

: jangkauan maksimal tetangga,

: konstanta perubahan jangkauan, n t     : banyak maksimal tetangga.

Langkah-langkah algoritma GSO ditunjukkan pada Gambar 2.

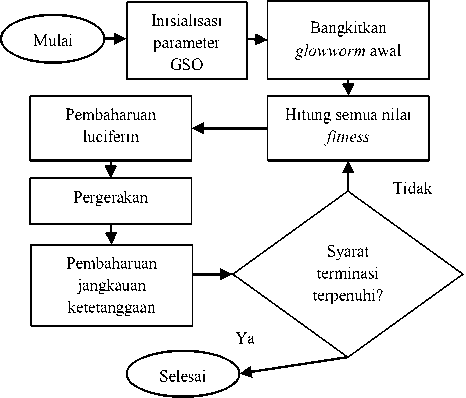
Gambar 2. Diagram Alir GSO (Sumber: Oramus, 2010)

  • 3.    HASIL DAN PEMBAHASAN

Penelitian ini menggunakan data sekunder kecelakaan lalu lintas tiap kecamatan di Bali tahun 2017 yang diambil dari penelitian Utari dkk. (2019). Data terdiri dari satu variabel terikat (Y) dan tiga variabel bebas (X) yaitu: Y = jumlah kecelakaan lalu lintas, ^l = kepadatan penduduk (jiwa/km2), ^2 = rata-rata curah hujan (mm), ^3 = penduduk usia 15-29 tahun (jiwa).

Penelitian tersebut menyatakan bahwa terdapat heterogenitas spasial pada data yang digunakan. Selain itu, diperoleh kesimpulan bahwa model GWR dengan kernel adaptif Gaussian adalah model terbaik untuk kasus pada penelitian tersebut. Dengan mengacu pada hasil penelitian Utari dkk, tahapan analisis pada penelitian ini dijabarkan sebagai berikut:

  • 1 . Menghitung statistik deskriptif data dan jarak antar daerah.

  • 2 . Menentukan bandwidth optimal berdasarkan nilai CV menggunakan algoritma KNN dan GSO.

  • 3 . Menentukan      estimasi      model

menggunakan algoritma KNN dan GSO.

  • 4 . Membandingkan kinerja algoritma KNN dan GSO berdasarkan koefisien determinasi dan running time.

Khusus untuk algoritma GSO, parameter algoritma    diperoleh dari    penelitian

Krishnanand dan Ghose (2005) dengan modifikasi   pada beberapa   parameter.

Parameter GSO meliputi p = 0,4; Y = 0,6; θ = 0,08; nt=5; S = 0,2; dan rs = 150.

Nilai S dan rs dimodifikasi untuk menyesuaikan dengan rentang jarak antar daerah. Selain itu, individu yang dibangkitkan ada sebanyak 5 dengan iterasi sebanyak 500 dan percobaan dilakukan sebanyak 10 kali. Aplikasi yang digunakan adalah Matlab R2015a.

  • 3 .1 Perhitungan Statistik Deskriptif Data

Statistik deskriptif data mengacu pada penelitian Utari dkk. (2019). Hasil statistik deskriptif ditampilkan pada Tabel 1.

Tabel 1. Statistik Deskriptif Data

Variabe l

Rataan

Simpanga n Baku

Minimu m

Maksimu m

Y

33,91

31,784

6

147

1.253,39

1.382,407

162

6009

Y2

223,32

70,314

93,250

393,125

Y3

17.223,3

3

17.000,17

6

2.960

92.540

Sumber: (Utari dkk., 2019)

Berdasarkan Tabel 1 dapat dilihat bahwa rataan kecelakaan (Y), kepadatan penduduk ( ^l), dan jumlah penduduk usia 15-29 tahun ( ^3 ) lebih mendekati nilai minimum dengan simpangan yang hampir sama besar dengan rataannya. Ini berarti terdapat beberapa daerah dengan nilai yang jauh melampaui daerah lainnya. Diperoleh bahwa daerah tersebut merupakan daerah sekitar Kota Denpasar.

Lain halnya dengan rata-rata curah hujan ( ^2) yang nilainya tidak terlampau jauh antar daerah. Rata-rata curah hujan berada antara rentang 90 mm hingga 400 mm dengan curah hujan terendah terjadi di derah Seririt dan tertinggi di daerah Bebandem.

Selanjutnya untuk mencari jarak antar daerah digunakan persamaan (1) dengan mentransformasikan letak astronomis masing-masing daerah ke dalam satuan jarak (kilometer). Setelah jarak antar daerah diperoleh maka dilanjutkan dengan penentuan bandwidth optimal.

  • 3 .2 Penentuan Bandwidth Optimal pada

    Algoritma KNN dan GSO

Perhitungan bandwidth optimal pada algoritma KNN dan GSO mengalami proses yang berbeda. Hal ini dikarenakan algoritma KNN yang merupakan algoritma deterministik yang selalu menghasilkan nilai tetap, sedangkan algoritma GSO merupakan algoritma probabilistik yang menghasilkan

nilai tidak tetap. Hasil untuk beberapa daerah dapat dilihat pada Tabel 2.

Tabel 2. Bandwidth dan Nilai CV

Daerah

Bandwidth

KNN

GSO

Tabanan (D1)

13,24

113,9 ± 0,02

Klungkung (D2)

14,05

20,75±0

Jembrana (D3)

40,11

7,46 ± 0,4

Nilai CV

194,06

136,8 ± 0,91

Sumber: Data diolah (2019).

Tabel 2 memperlihatkan bahwa beberapa daerah memiliki bandwidth optimal yang berbeda. Selain itu, nilai CV pada GSO lebih kecil daripada nilai CV pada KNN. Ini berarti algoritma GSO mampu mencari bandwidth yang lebih optimal daripada algoritma KNN. Setelah mendapatkan bandwidth optimal kemudian dilanjutkan dengan mencari matriks pembobot dan estimasi parameter model.

  • 3 .3 Penentuan Estimasi Model pada

    Algoritma KNN dan GSO

Estimasi model diperoleh dengan mencari estimasi parameter berdasarkan persamaan (4). Hasil untuk beberapa amatan dapat dilihat pada Tabel 3.

Tabel 3. Estimasi Parameter Model

Daerah

KNN

β0

βl

β2

β3

D1

52,05

0,0028

-0,179

0,0014

D2

16,29

0,01

-0,059

0,0010

D3

25,74

0,0052

-0,088

0,0013

Daerah

GSO

β0

βl

β2

β3

D1

24,39

0,0073

-0,082

0,0010

D2

20,40

0,0085

-0,069

0,0010

D3

-3,20

-0,0658

0,017

0,0039

Sumber: Data diolah (2019).

Estimasi parameter model pada Tabel 3 menggunakan algoritma KNN dan GSO berbeda. Perbedaan ini disebabkan oleh pemilihan bandwidth optimal yang berlainan. Hal ini memperjelas bahwa pemilihan bandwidth memengaruhi estimasi model yang diperoleh. Contohnya adalah estimasi model daerah Jembrana (D3) yaitu untuk algoritma KNN:

yD3 =25,74 + 0,0052*1 - 0,088χ2 + 0,0013χ3 sedangkan untuk algoritma GSO:

Vds =-3,20 - 0,0658Xi + 0,017X2 + 0,0039x3

Terlihat bahwa koefisien beberapa variabel pada algoritma KNN menjadi terbalik (berlawanan tanda) pada algoritma GSO. Sebagai perbandingan, estimasi model daerah Jembrana menggunakan algoritma KNN menunjukkan bahwa setiap kenaikan satu satuan kepadatan penduduk (^l ) akan mengakibatkan kenaikan angka kecelakaan (y) sebesar 0,0052 satuan. Namun, kenaikan satu satuan kepadatan penduduk ( Xi) pada estimasi model menggunakan algoritma GSO justru akan menurunkan angka kecelakaan (y) sebesar 0,0658 satuan. Hal yang serupa terjadi pada rata-rata curah hujan (X2). Selain itu, kenaikan satu satuan penduduk usia 15 – 29 tahun ( X3 ) pada estimasi model dengan algoritma KNN akan meningkatkan angka kecelakaan (y) sebesar 0,0013 satuan, sedangkan pada estimasi model dengan algoritma GSO justru menjadi tiga kali lipat yaitu meningkatkan angka kecelakaan (y) sebesar 0,0039 satuan. Estimasi model lainnya juga diinterpretasikan dengan cara serupa.

  • 3 .4 Perbandingkan Kinerja Algoritma

    KNN dan GSO

Setelah estimasi model diperoleh, nilai koefisien determinasi dapat dihitung menggunakan persamaan (6). Selain memperhatikan nilai koefisien determinasi, masing-masing algoritma juga menampilkan durasi (running time) yang diperlukan untuk membentuk estimasi model. Hasil perbandingan kinerja algoritma dapat dilihat pada Tabel 4.

Tabel 4. Perbandingan Kinerja Algoritma

KNN

GSO

R2 (%)

90,64

95,21 ± 1,2

Durasi (s)

1,79 ± 0,23

180,73 ± 1,43

Sumber: Data diolah (2019).

Berdasarkan Tabel 4 diperoleh bahwa nilai rata-rata koefisien determinasi yang diperoleh algoritma GSO lebih besar daripada algoritma KNN. Di lain sisi, durasi algoritma GSO justru jauh lebih lambat daripada algoritma KNN. Ini berarti pemilihan bandwidth yang lebih optimal pada algoritma GSO akan diikuti oleh durasi algoritma yang lebih lambat.

  • 4.    KESIMPULAN DAN SARAN

    • 4.1    Kesimpulan

Berdasarkan pembahasan yang telah dijabarkan maka diperoleh bahwa algoritma GSO mampu menghasilkan bandwidth yang lebih optimal daripada algoritma KNN, tetapi durasi yang diperlukan untuk menghasilkan estimasi model akan jauh lebih lambat.

  • 4.2    Saran

Berdasarkan kesimpulan yang diperoleh maka saran yang dapat diberikan yaitu:

  • 1.    Parameter, jumlah individu, maupun iterasi pada algoritma GSO dapat dimodifikasi agar durasi (running time) algoritma tersebut lebih cepat.

  • 2.    Penelitian berikutnya dapat menggunakan algoritma probabilistik lainnya atau deterministik.

DAFTAR PUSTAKA

Caraka, R.E. & Yasin, H. 2017.

Geographically Weighted Regression (GWR) Sebuah Pendekatan Regresi Geografis. First ed. Yogyakarta: Mobius.

Krishnanand, K.N. & Ghose, D. 2006.

Glowworm Swarm Based Optimization

Algorithm for Multimodal Function with Collective     Robotic     Applications.

Multiagent and Grid System – An International Jurnal. Volume 2. Hal 209 – 222.

Krishnanand, K.N. & Ghose, D. 2009. Glowworm Swarm Optimization for Simultaneous Capture of Multiple Local Optima of Multimodal Functions. Swarm Intell. Volume 3. Hal 87 – 124.

Oramus, Piotr. 2010. Improvements to Glowworm    Swarm    Optimization

Algorithm. Computer Science. Volume 10. Hal 7 – 20.

Sutton, Oliver. 2012. Introduction to k Nearest Neighbour Classification and Condensed Nearest Neighbour Data Reduction. Leicester: University of Leicester.

Utari, N. K. E. Y. Srinadi, I G. A. M. & Susilawati     M.     2019.     Model

Geographically Weighted Regression (GWR) Faktor-Faktor yang Memengaruhi Kecelakaan Lalu Lintas di Provinsi Bali. E-Jurnal Matematika. Volume 8(2). Hal. 140 – 147.

84