PERHITUNGAN VALUE AT RISK KUNJUNGAN WISATAWAN ASING KE BALI

E-Jurnal Matematika Vol. 9(1), Januari 2020, pp.69-78

DOI: https://doi.org/10.24843/MTK.2020.v09.i01.p281

ISSN: 2303-1751

PERHITUNGAN VALUE AT RISK KUNJUNGAN WISATAWAN ASING KE BALI

Agus Putu Suryawan^1§, Komang Dharmawan², I Gusti Ayu Made Srinadi ³

¹Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: putusuryawan68@gmail.com]

²Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: dharmawan.komang@gmail.com]

³Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: srinadi@unud.ac.id]

^§Corresponding Author

ABSTRACT

The development of the tourism industry in Bali is very fast compared to other regions in Indonesia. This is due to the fascination of Bali which fascinates tourists, such as culture, customs and natural beauty. The rapid development of tourism in Bali requires tourism risk management. The purpose of this study is to calculate the Value At Risk (VaR) of Chinese, British and American tourists visiting Bali. The study was conducted using the VaR method with the GARCH (1,1) and GJR (1,1) models. Chinese tourist visit data is homocedasticity so it cannot proceed to GARCH (1.1) and GJR (1.1) modeling. VaR value of British and American tourist visits using the GARCH (1.1) and GJR (1.1) models at 95% confidence levels respectively -69.2% and -43.6 with an average VaR value of -56, 4%, and -69.3% and -44.7% with an average VaR of -57%. This means that if the Bali Government targets the number of tourist visits to be 7,100,000 people with a tourism promotion cost of Rp.134.1 per person, then there will be at least 4,004,400 people visiting Bali. So the investment costs incurred by the Provincial Government of Bali for tourism promotion of Rp. 536,990,040.

Keywords: Bali, GARCH, GJR, Tourism, Value At Risk

• 1.    PENDAHULUAN

Perkembangan industri pariwisata Indonesia dapat terlihat dari peningkatan kunjungan wisatawan asing dan domestik. Peningkatan yang terjadi memberikan dampak positif bagi negara pada sektor perekonomian, perdagangan dan perhotelan.

Bali merupakan salah satu tempat tujuan wisata yang sangat cepat berkembang di Indonesia. Data statistik menunjukan bahwa kunjungan wisatawan asing mengalami peningkatan setiap tahunnya, namun masih adanya perubahan setiap bulannya (Dinas Pariwisata Provinsi Bali, 2018).

Perubahan kunjungan wisatawan asing yang tidak tetap, mempunyai pengaruh terhadap pendapatan asli daerah dan perkembangan industri pariwisata. Berdasarkan hal tersebut maka pemerintah Provinsi Bali dan pelaku indutri pariwisata harus mengambil kebijakan yang tepat dalam perkembangan pariwisata. Agar kebijakan yang diambil menjadi lebih terukur dan tepat, maka perlu dilakukan penelitian manajemen risiko pariwisata.

J.P.Morgan memperkenalkan value at risk

(VaR) sebagai ukuran risiko yang umum digunakan dalam manajemen risiko finansial. Konsep perhitungan VaR dapat diterapkan dalam manajemen risiko pariwisata (Bunnag, et al., 2010).

Bunnag, et al. (2010) melakukan penelitian untuk mengetahui tingkat pertumbuhan dan risiko kunjungan wisatawan international yang datang ke Thailand. Penelitian ini menggunakan data kunjungan wisatawan Malaysia, Jepang, Inggris, dan Amerika Serikat. Metode yang digunakan pada penelitian ini adalah VaR dengan model GARCH dan GJR. Pada hasil penelitian diketahui bahwa VaR kunjungan wisatawan Malaysia lebih tinggi dari wisatawan Jepang, Inggris, dan Amerika.

Model GARCH merupakan salah satu model untuk mengestimasi volatilitas yang memiliki karakteristik respon yang simetris terhadap guncangan. sedangkan model GJR merupakan salah satu model volatilitas yang dapat mengakomodasi respon asimetris terhadap guncangan (Danielsson, 2001).

Penelitian ini bertujuan menghitung VaR kunjungan wisatawan asing yang datang ke Bali menggunakan model GARCH dan GJR.

• 2.    METODE PENELITIAN

Data yang digunakan penelitian ini adalah data sekunder kunjungan wisatawan Cina, wisatawan Inggris, dan wisatawan Amerika ke Bali yang diperoleh dari Dinas Pariwisata Provinsi Bali. Metode analisis pada penelitian ini adalah Value At Risk, dimana software yang digunakan adalah R.3.6.1. Adapun langkah-langkah yang dilakukan sebagai berikut: 1. Identifikasi Stasioneritas

Data deret waktu belum dapat dianalisis apabila data deret waktu belum memenuhi asumsi kestasioneran. Kestasioneran pada data dapat diketahui dengan menggunakan Uji augmented Dickey-Fuller(ADF). Hipotesis dari uji ini adalah:

Hq ∶ Data tidak stasioner

H^ ∶ Data stasioner

Keputusan penolakan Hq adalah ketika P- value<α.

Apabila data memenuhi asumsi stasioner dapat dilakukan proses differencing, dimana proses differencing dapat dinyatakan sebagai berikut:

∇X_t =    [ Γ^ ]=logXt ^- logX_t.₁. (1)

dimana nilai ∇ merupakan log-return dari suatu data pada waktu ke-t, Xt—i merupakan nilai data pada waktu ke-t-1, dan Xt merupakan nilai data pada waktu ke-t, dengan t=1,2,3,…,n.

• 2.    Identifikasi Model Rataan

Model deret waktu terdiri dari:

• 1)    Model Autoregressive (AR)

Model autoregressive dengan orde P dinotasikan dengan AR( P). Bentuk umum model AR( P) yaitu:

x_t = + Φ1X_t-1 + Φ2X_t-2+⋯ +ΦpX_t-p + ^ε_t

dimana P menyatakan konstanta, Φι, Φ2,…,Φp menyatakan parameter autoregressive ke-i, ^t menyatakan nilai error pada periode t, Xt-I,…,Xt—p menyatakan variabel bebas, dan P menyatakan order dari model autoregressive (AR).

• 2)    Model Moving Average (MA)

Model lain dari ARIMA adalah moving average yang dinotasikan dalam MA (q)

atau ARIMA (0,0,P ) yang ditulis dalam persamaan berikut:

X_t = + ε_t ^- Q1^ε_t-1 ^- Q2^ε_t-2 -⋯

-Θp^ε_t-p

dimana P menyatakan konstanta, ^l , ^2 ,…,Qp menyatakan parameter moving average, dan ^t-1,…, ^t-Q menyatakan selisih nilai aktual dengan nilai peramalan.

• 3)    Model Seasonal Autoregressive Integrated Moving Average (SARIMA)

Model SARIMA  merupakan  model

ARIMA  yang mengandung  unsur

musiman.   Secara umum,   bentuk

persamaan  model  persamaan  model

SARIMA adalah:

ΦV(B_)Φ ∗₍B^s)(1-B)d(1-B^s)^Dx_t =   (B)θ∗₍B^s) ^ε_t

dimana Φ ^∗ menyatakan parameter seasonal autoregressive (SAR) orde P,θ∗ menyatakan parameter seasonal moving autoregressive (SMA) orde  Q,  Φp

menyatakan parameter autoregressive (AR) orde P, Qq menyatakan parameter moving average (MA) orde P, (1-B)d menyatakan differencing non musiman orde d,    (1-B^s)^D    menyatakan

differencing musiman orde  D,  P,Q

menyatakan orde musiman AR (SAR) dan musiman MA (SMA), P,P menyatakan orde non musiman AR dan MA, dan S menyatakan panjang periode musiman. Langkah-langkah prosedur menentukan model rataan adalah sebagai berikut:

• a.    Identifikasi Model

Identifikasi model diperoleh dengan melihat korelogram ACF dan PACF, dimana orde AR(p) dan MA( P) diperoleh dari grafif ACF dan PACF.

Tabel 1. Identifikasi Orde Model

Proses	ACF	PACF
AR(p)	Tails off	Cut off lag p
MA(q)	Cut off lag p	Tails off

• b.    Pendugaan Parameter Model Pendugaan parameter dilakukan melalui uji signifikan parameter. Jika koefesien tidak signifikan maka model tersebut tidak layak digunakan.

Hipotesis dari uji ini adalah:

Hq ∶ Parameter tidak signifikan

Hy ∶ Parameter signifikan

Keputusan penolakan Hq adalah ketika

P- value<α.

• c.    Pemeriksaan Model

Pemeriksaan dilakukan dengan mengamati residual model apakah sudah berditribusi normal dan apakah residual dari model mempunyai autokorelasi atau tidak. Kenormalan sisaan dari suatu model dapat diketahui dengan melakukan uji Jarque-Bera. Hipotesis dari uji ini adalah sebagai berikut:

Hq ∶ Residual berditribusi normal

Hy ∶ Residual tidak berditribusi normal Keputusan penolakan Hq adalah ketika P- value<α.

Uji autokorelasi dapat digunakan uji -white noise. Hipotesis dari uji ini adalah sebagai berikut:

Hq ∶ Residu white noise

Hy ∶ Residu tidak white noise

Keputusan penolakan Hq adalah ketika P- value<α.

• d.    Pemilihan Model Terbaik

Kriteria yang digunakan untuk pemilihan model terbaik berdasarkan residual menggunakan nilai AIC minimum (Wei, 2006) yaitu sebagai berikut:

AIC (M)=n ln ̂ a +2M.     (2)

dengan n adalah banyaknya residual, M adalah jumlah parameter di dalam model, dan ̂ a varians dari residual

• 3.    Melakukan Analisis Model GARCH dan GJR

Langkah-langkah analisis model GARCH dan GJR adalah sebagai berikut:

• a.    Uji Efek ARCH-LM

Menurut Tsay (2002) uji ARCH-LM dapat digunakan untuk mendeteksi keberadaan heterokedastisitas dan keberadaan efek ARCH pada deret waktu. Hipotesis dari uji ini adalah sebagai berikut:

Hq ∶ Residu white noise

Hy ∶ Residu tidak white noise

Keputusan penolakan Hq adalah ketika P- value<α.

• b.    Menduga Parameter Model GARCH

Model GARCH adalah pengembangan dari model ARCH yang diusulkan oleh Engel pada tahun 1982. Model GARCH dapat dinyatakan (Tsay, 2002):

σ_t =  + α_i⅛₂ + βι⅛-ι+⋯

+βq^σ_t-q                 (3)

Metode yang dapat digunakan untuk mengestimasi model GARCH adalah metode     maxsimum     likelihood

estimasion (MLE) yang dapat didefinisikan sebagai berikut (Wei, 2006):

1

Y_t =    ⁺       _π_____(4)

1-φ_tB -⋯-φ_po^p

• c.    Menduga Parameter Model GJR Glosten, Jagannathan, dan Runkle mengembangkan model GARCH yang mengakomodasi leverage effect. Model GJR dapat dinyatakan sebagai berikut:

∑

(ai^εt-i ⁺ Yi^εt-iβ-i) i=ι

∑

. βrf-i

j-i

(5)

dengan Λ-i ={ _l

1, ^εt-i<0,

0, ^εt-i≥0,

^εt =

• 4.    Perhitungan Value At Risk

Value at Risk (VaR) merupakan suatu ukuran risiko untuk menghitung kerugian maksimum dengan tingkat kepercayaan pada periode waktu tertentu yang diperkenalkan oleh J.P. Morgan pada tahun 1994. Perhitungan VaR kunjungan wisatawan menggunakan metode parametrik dapat diestimasi menggunakan persamaan (McAleer, et al., 2005):

VaR=P+z√ ^σt (6)

Dimana P adalah peramalan tingkat pertumbuhan kunjungan pada waktu ke-t , ^σi adalah volatilitas pada waktu ke-t, dan Z adalah confidence factor.

• 3.    HASIL DAN PEMBAHASAN

Identifikasi Data

Identifikasi data dilakukan sebagai bahan acuan untuk analisis tahap selanjutnya. Data kunjungan wisatawan Cina, wisatawan Inggris, dan wisatawan Amerika ke Bali periode Januari 2010 sampai Desember 2018 digunakan pada penelitian kali ini yang bersumber dari Dinas Pariwisata Provinsi Bali.

Kunjungan Wisatawan Cina, Inggris, dan Amerika ke Bali

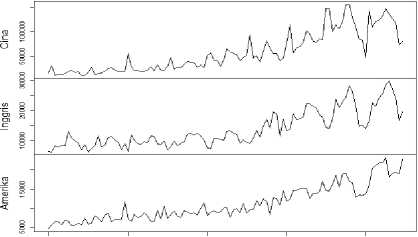
2010               2012               2014               2016               2018

Tahun

Gambar 1. Data Kunjungan Wisatawan Cina, Inggris, dan Amerika ke Bali

Gambar 1 menunjukan jumlah kunjungan wisatawan Cina, wisatawan Inggris, dan Amerika ke Bali mengalami tren naik setiap tahunnya namun masih adanya fluktuasi setiap bulannya. Penurunan yang signifikan terjadi pada akhir tahun 2017. Hal ini diperkirakan karena erupsi Gunung Agung yang mengganggu pariwisata Bali. Kunjungan wisatawan ke Bali berangsur-angsur mengalami peningkatan pada awal tahun 2018 yang secara umum mengalami tren naik.

Bunnag, et al. (2010) dalam mengestimasi nilai VaR kunjungan wisatawan, menggunakan differencing dari kunjungan wisatawan internasional yang datang ke Thailand. Oleh karena itu, penelitian ini berfokus pada memanajemen risiko pariwisata menggunakan return kunjungan wisatawan Cina, wisatawan Amerika, dan wisatawan Amerika. Data dikonversi     menjadi    return     dengan

menggunakan persamaan (1) dan secara grafis diberikan pada Gambar 2.

DifferencingWisatawan Cina₅ Inggris, dan Amerika ke Bali

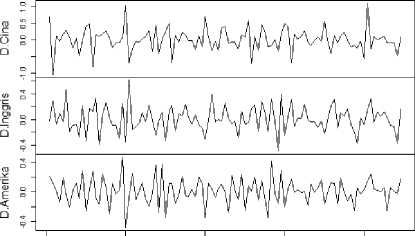
2010               2012               2014               2016               2018

Tahun

Gambar 2. Differencing Kunjungan Wisatawan Inggris, dan Amerika ke Bali

Suatu data deret waktu belum dapat dianalis apabila data tersebut belum memenuhi asumsi kestasioneran. Identifikasi stasioneritas pada data return kunjungan wisatawan Cina,

Inggris dan Amerika dilakukan dengan menggunakan uji augmented Dickey-Fuller (ADF). Uji return kunjungan wisatawan Cina, Inggris, dan Amerika ke Bali diberikan pada Tabel 2

Tabel 2. Uji ADF Return Kunjungan Wiatawan Cina, Inggris, dan Amerika ke Bali

Uji Formal (a = 0,05)	р-value
	Cina	Inggris	Amerika
Uji ADF	0,01	0,01	0,01

Sumber : Data diolah (2019)

Tabel 2 uji ADF dengan taraf signifikan a = 0,05 pada data differencing kunjungan wisatawan Cina, Inggris, dan Amerika ke Bali menunjukan р-value kurang dari taraf signifikan a. sehingga tolak hipotesis nol. Hal ini berarti tidak terdapat akar unit. Maka data return kunjungan wisatawan Inggris, dan Amerika ke Bali stasioner.

Mengidentifikasi Model

Setelah diperoleh kestasioneran data, selanjutnya dilakukan identifikasi orde P,d,Q dari model. Orde P,d,Q dapat diketahui dari korelogram fungsi autokorelasi (ACF) dan fungsi autokorelasi parsial (PACF).

senes as.vector Return

series as.vector Return

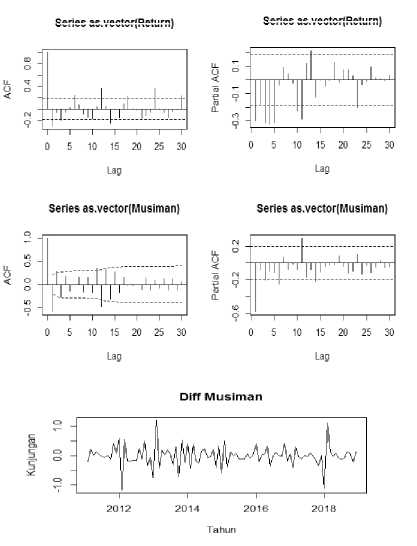
Gambar 3. Plot ACF dan PACF Return, ACF dan PACF Musiman, dan Diff Musiman Cina

Gambar 3. menunjukan korelogram ACF return, data cut off setelah lag 0, sehingga diduga orde model MA yaitu Q =0. Sedangkan pada pada korelogram PACF return diketahui

cut off setelah lag 1, sehingga diduga orde model AR yaitu p = 1. Pada korelogram ACF dan PACF return, terlihat bahwa data masih mengandung unsur musiman, karena memiliki lag yang berulang pada lag 12, 24 maka dilakukan differencing musiman untuk menghilangkan pengaruh musiman pada data.

Gambar 3 memperlihatkan korelogram ACF musiman, data cut off setelah lag 0, sehingga diduga orde model SMA yaitu Q = 0. Sedangkan pada korelogram PACF musiman diketahui cut off setelah lag 1, sehingga diduga orde model SAR yaitu P = 1. Karena ACF dan PACF data differencing musiman sebanyak satu kali, diperoleh orde D = 1. Sehingga dugaan model sementara adalah sebagai berikut: SARIMA(1,0,0)(0,1,1) ¹².

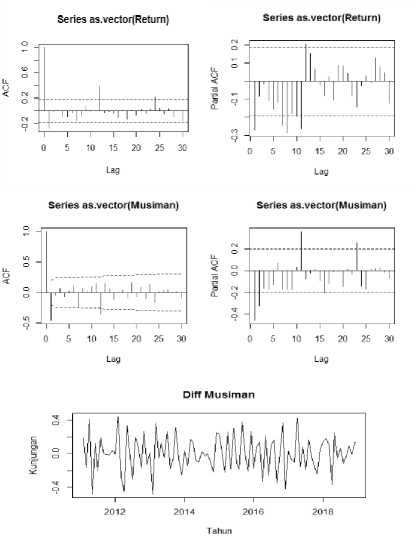
Gambar 4. Plot ACF dan PACF Return, ACF dan PACF Musiman, dan Diff Musiman Inggris

Gambar 4. menunjukan korelogram ACF return, data cut off setelah lag 0, sehingga diduga orde model MA yaitu p = 0. Sedangkan pada pada korelogram PACF return diketahui cut off setelah lag 1, sehingga diduga orde model AR yaitu p = 1. Pada korelogram ACF dan PACF return, terlihat bahwa data masih mengandung unsur musiman, karena memiliki lag yang berulang pada lag 12, 24 maka dilakukan differencing musiman untuk menghilangkan pengaruh musiman pada data.

Gambar 4. menunjukan korelogram ACF musiman, data cut off setelah lag 0, sehingga

diduga orde model SMA yaitu Q = 0. Sedangkan pada korelogram PACF musiman diketahui cut off setelah lag 2, sehingga diduga orde model SAR yaitu P = 2. Karena ACF dan PACF data differencing musiman sebanyak satu kali, diperoleh orde D = 1. Sehingga dugaan model sementara adalah sebagai berikut: SARIMA(1,0,0)(2,1,0) ¹² .

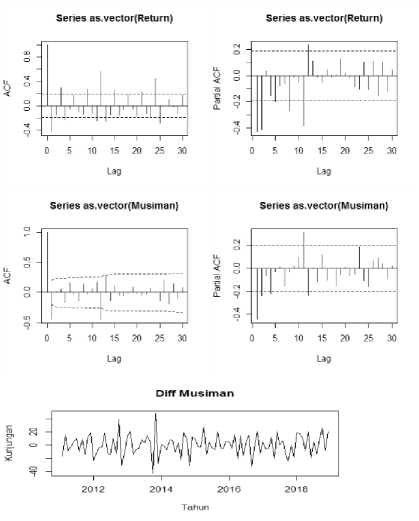
Gambar 5. menunjukan korelogram ACF return, data cut off setelah lag 0, sehingga diduga orde model MA yaitu p = 0. Sedangkan pada pada korelogram PACF return diketahui cut off setelah lag 2, sehingga diduga orde model AR yaitu p = 2. Pada korelogram ACF dan PACF return, terlihat bahwa data masih mengandung unsur musiman, karena memiliki lag yang berulang pada lag 12, 24 maka dilakukan differencing musiman untuk menghilangkan pengaruh musiman pada data.

Gambar 5. menunjukan korelogram ACF musiman, data cut off setelah lag 0, sehingga diduga orde model SMA yaitu Q = 0. Sedangkan pada korelogram PACF musiman diketahui cut off setelah lag 2, sehingga diduga orde model SAR yaitu P = 2. Karena ACF dan PACF data differencing musiman sebanyak satu

kali, diperoleh orde D = 1. model sementara adalah SARIMA(2,0,0)(2,1,0) ¹² .

Menduga Parameter

Pendugaan parameter melakukan penaksiran nilai

Sehingga dugaan sebagai berikut:

model yaitu parameter untuk

semua model yang diduga. Setelah mendapatkan model, selanjutnya menduga

parameter dari setiap model dimana р-value kurang dari taraf signifikan a = 0,05. Berikut diberikan hasil pendugaan parameter beberapa model dugaan menggunakan software R.3.6.1:

Tabel 3. Uji Signifikansi Parameter Beberapa Model Wisatawan Cina.

Model	Parameter	р-value
SARIMA(1,1,1) (0,1,1) 12         ∖	MA(1)	0,0000
	SMA(1)	0,0000
SARIMA(2,0,1) (0,1,0) 12         ∖	AR(1)	0,0450
	AR(2)	0,0005
	MA(1)	0,0000
SARIMA(0,0,2) (2,1,1) 12         ∖	MA(1)	0,0000
	MA(2)	0,2496
	SAR(1)	0,0000
	SAR(2)	0,0000
	SMA(1)	0,0001
SARIMA(1,0,2) (1,1,1) 12         ∖	AR(1)	0,0007
	MA(1)	0,0000
	MA(2)	0,0721
	SAR(1)	0,1745
	SMA(1)	0,0000
SARIMA(1,0,1) (0,1,2) 12         ∖	AR(1)	0,4632
	MA(1)	0,0000
	SMA(1)	0,0002
	SMA(2)	0,2066

Sumber: Data diolah (2019)

Tabel 3 menunjukan model dugaan wisatawan cina SARIMA(2,0,1)(0,1,0) 12 , dan SARIMA(0,0,1)(0,1,1)12 р-value parameternya kurang dari taraf signifikan a = 0,05. Sehingga tolak hipotesis nol. Hal ini berarti parameternya signifikan.

Tabel 4. Uji Signifikansi Parameter Beberapa Model Wisatawan Inggris.

Model	Parameter	р-value
SARIMA(3,0,0) (0,1,0) 12         ∖	AR(1)	0,0000
	AR(2)	0,0002
	AR(3)	0,0792
SARIMA(2,0,0) (0,1,0) 12         ∖	AR(1)	0,0000
	AR(2)	0,0011
SARIMA(1,0,0) (2,1,0) 12         ∖	AR(1)	0,0000
	SAR(1)	0,0000
	SAR(2)	0,0000
SARIMA(0,0,2) (0,1,1) 12         ∖	AR(1)	0,0007
	MA(1)	0,0000
	MA(2)	0,0721
	SAR(1)	0,1745
	SMA(1)	0,0000
SARIMA(1,0,1) (0,1,2) 12         ∖	AR(1)	0,4632
	MA(1)	0,0000
	SMA(1)	0,0002
	SMA(2)	0,2066

Sumber: Data diolah (2019)

Tabel 4 menunjukan model dugaan wisatawan Inggris SARIMA(2,0,1)(0,1,0)12 , dan SARIMA(1,0,0)(2,1,0)12 р-value parameternya kurang dari taraf signifikan a = 0,05 sehingga tolak hipotesis nol. Hal ini berarti parameternya signifikan.

Tabel 5. Uji Signifikansi Parameter Beberapa Model Wisatawan Amerika.

Model	Parameter	р-value
SARIMA(2,0,0) (2,1,0) 12         ∖	AR(1)	0,0000
	AR(2)	0,0002
	SAR(1)	0,0792
	SAR(2)	0,0228
SARIMA(0,0,1) (0,1,1) 12         ∖	MA(1)	0,0000
	SMA(1)	0,0000
SARIMA(2,0,1) (0,1,0) 12         ∖	AR(1)	0,0068
	AR(2)	0,0570
	MA(1)	0,0000
SARIMA(1,0,0) (2,1,1) 12         ∖	AR(1)	0,0000
	SAR(1)	0,8136
	SAR(2)	0,8380
	SMA(1)	0,1286
SARIMA(1,0,2) (2,1,1) 12         ∖	AR(1)	0,2352
	MA(1)	0,9491
	SAR(1)	0,0591
	SAR(2)	0,1929
	SMA(1)	0,1532

Sumber: Data diolah (2019)

Tabel 5. Menunjukan model dugaan wisatawan amerika SARIMA(0,0,1)(0,1,1)12 dengan р-value parameter kurang dari taraf signifikan a = 0,05. Sehingga tolak hipotesis nol. Hal ini berarti parameternya signifikan.

Uji Kenormalan dan White Noise pada Residual (Sisaan)

Setelah dilakukan pendugaan parameter. langkah selanjutnya melihat kenormalan sisaan menggunakan uji jarque-bera dan uji white noise pada residual model.

Tabel 6. Uji Kenormalan dan White Noise Wisatawan Cina

Model	Uji jarque-bera	Uji White Noise	AIC
SARIMA(0,0,1) (0,1,1) 12         ∖	2,2 ×10 -16  ∖	0,605	3,04
SARIMA(2,0,0) (0,1,0) 12         ∖	2,2 ×10 -16  ∖	0,131	39,64
SARIMA(0,0,2) (2,1,1) 12         ∖	2,2 ×10 -16  ∖	0,986	2,09
SARIMA(0,0,2) (2,1,1) 12         ∖	2,2 ×10 -16  ∖	0,963	4,59
SARIMA(1,0,1) (0,1,2)12         ∖	2,2 ×10 -16	0,921	3,43

Sumber: Data diolah (2019)

Tabel 6 untuk uji kenormalan residual semua model dugaan р-value kurang dari taraf signifikan a = 0,05 sehingga cukup bukti tolak hipotesis nol. Hal ini mengindikasikan bahwa semua model dugaan tidak berditribusi normal. Apabila model tidak berdistribusi normal maka hasil peramalan yang dilakukan kurang akurat. Uji white noise semua model diperoleh р-value lebih besar dari taraf signifikan a = 0,05 sehingga tolak hipotesis nol. Hal ini berarti mengindikasikan masing-masing model white noise.

Setelah dilakukan uji kenormalan, dan uji white noise. selanjutnya memilih model terbaik yang memenuhi signifikansi parameter, uji white noise dan nilai AIC minimum. Sehingga model yang memenuhi asumsi tersebut adalah model SARIMA(0,0,1)(0,1,1)12

Tabel 7. Uji Kenormalan dan White Noise Wisatawan Inggris

Model	Uji jarque-bera	Uji White Noise	AIC
SARIMA(3,0,0) (0,1,0) 12	0,522	0,507	-52,39
SARIMA(2,0,0) (0,1,0) 12	0,245	0,231	-51,29
SARIMA(1,0,0) (2,1,0) 12         ∖	0,396	0,009	-73,3
SARIMA(0,0,2) (0,1,1) 12         ∖	0,025	0,698	-91,11
SARIMA(1,0,1) (0,1,2)12         ∖	0,026	0,890	-90,79

Sumber: Data diolah (2019)

Tabel 7. untuk uji kenormalan residual model dugaan SARIMA(3,0,0)(0,1,0)12 , SARIMA (2,0,0)(0,1,0)12 , dan SARIMA(1,0,0)(2,1,0)12 diperoleh р-value lebih besar dari taraf signifikan a = 0,05 sehingga tolak hipotesis nol. Hal ini mengindikasikan bahwa model berditribusi normal. Uji white noise model dugaan SARIMA(3,0,0)(0,1,0)12 , SARIMA (2,0,0)(0,1,0)12,SARIMA(0,0,2)(0,1,1)12 ,dan SARIMA(1,0,1)(0,1,2)12 diperoleh р-value lebih besar dari taraf signifikan a = 0,05 sehingga tidak cukup bukti tolak hipotesis nol. Hal ini berarti masing-masing model white noise.

Setelah dilakukan uji kenormalan, dan uji white noise. selanjutnya memilih model terbaik yang memenuhi signifikansi parameter, uji kenormalan, uji white noise dan nilai AIC minimum. Sehingga model yang memenuhi

asumsi tersebut adalah model SARIMA (2,0,0) (0,1,0) 12 .

Tabel 8. Uji Kenormalan dan White Noise Wisatawan Amerika

Model	Uji jarque-bera	Uji White Noise	AIC
SARIMA(2,0,1) (2,1,0) 12         ∖	0,116	0,761	-130,27
SARIMA(0,0,1) (0,1,1) 12         ∖	0,051	0,461	-135,1
SARIMA(2,0,1) (0,1,0) 12         ∖	0,905	0,546	-105,07
SARIMA(1,0,0) (2,1,1) 12         ∖	0,302	0,195	-122,71
SARIMA(1,0,2) (2,1,1)12         ∖	0,001	0,582	-128,03

Sumber: Data diolah (2019)

Tabel 8. untuk uji kenormalan residual model dugaan SARIMA(1,0,2)(2,1,1) 12 diperoleh р-value kurang dari dari taraf signifikan a = 0,05 sehingga tidak cukup bukti tolak hipotesis nol. Hal ini mengindikasikan bahwa model tidak berditribusi normal. Uji white noise semua model dugaan diperoleh р-value lebih besar dari taraf signifikan a = 0,05. Hal ini berarti masing-masing model white noise.

Setelah dilakukan uji kenormalan, dan uji white noise. selanjutnya memilih model terbaik yang memenuhi signifikansi parameter, uji kenormalan, uji white noise dan nilai AIC minimum. Sehingga model yang memenuhi asumsi tersebut adalah model SARIMA (0,0,1) (0,1,1) 12 .

Uji Efek ARCH

Menurut Tsay (2002) uji ARCH-LM dapat digunakan untuk mendeteksi keberadaan heterokedastisitas bersyarat atau keberadaan efek ARCH pada deret waktu. Dalam melakukan uji pengaruh ARCH model yang akan diuji untuk data kunjungan Cina menggunakan residual model SARIMA(0,0,1)(0,1,1)12 , wisatawan Inggris menggunakan residual model SARIMA(2,0,0)(0,1,0)12 dan kunjungan wisatawan Amerika ke Bali menggunakan residual model SARIMA(0,0,1)(0,1,1)12 . Berdasarkan Tabel 9. uji ARCH-LM kunjungan wisatawan Inggris dan Amerika menunjukan р-value kurang dari taraf signifikana = 0,05 sehingga tolak hipotesis nol. Hal ini berarti terdapat efek ARCH pada kedua residual

model. Sedangkan kunjungan wisatawan Cina menunjukan р-value lebih besar dari taraf signifikan a = 0,05 sehingga tidak cukup bukti untuk menolak hipotesis nol. Hal ini berarti tidak terdapat efek ARCH dan bersifat homokedastisitas.

Tabel 9. Uji ARCH-LM

Uji Formal (a = 0,05)	р-value Kunj		ungan
	Cina	Inggris	Amerika
Uji ARCH-LM	0,9999	0,0427	0,01835
F-statistic	0,08513	2,002	2,314

Sumber: Data diolah (2019)

Estimasi Parameter Model GARCH

Metode yang dapat digunakan untuk mengestimasi parameter model GARCH adalah maxsimum likelihood estimasion (MLE). Estimasi model GARCH(1,1) dibantu dengan menggunakan software R.3.6.1 Data output pemodelan parameter GARCH(1,1) dapat dilihat pada Tabel 10.

Tabel. 10. Estimasi Parameter Model GARCH

Parameter	GARCH(1,1)
	Inggris	Amerika
ω	0,001728	0,001489
α1	0,000000	0,393079
^l	0,945142	0,549453
AIC	-0,61723	-1,6815
Uji Ljung-Box	0,2633	0,5243

Sumber : Data diolah (2019)

Berdasarkan Tabel 10. kondisi stasioner pada model GARCH(1,1) terpenuhi oleh hasil penjumlahan koefesien ARCH(1) dan koefesien GARCH(1,1) untuk masing-masing kunjungan wisatawan berlaku α₁ + βl<1. Disisi lain, nilai-nilai koefesien model GARCH(1,1) yaitu a₁≥0,βγ≥0 menunjukan bahwa kondisi positif pada varians model GARCH(1,1) berhasil dipertahankan.

Setelah mendapatkan model, perlu dilakukan uji asumsi pada residual model. Salah satu asumsi model GARCH adalah dilakukannya pengujian efek autokorelasi pada residual model, guna mengetahui keefektifan model dalam mengakomadasi keberadaan autokorelasi (Al-Ajez, 2016). Berdasarkan Tabel 10. р-value uji Ljung-Box masing-masing residual model lebih besar dari taraf signifikan a = 0,05, sehingga tidak cukup bukti tolak hipotesis nol. Hal ini mengindikasikan adanya efek autokorelasi pada residual model.

Estimasi Parameter GJR

Metode yang dapat digunakan untuk mengestimasi parameter model GJR adalah maxsimum likelihood estimasion (MLE). Estimasi model GJR(1,1) dibantu dengan menggunakan software R.3.6.1 dengan menggunakan package “rugarch”. Data output pemodelan parameter GJR(1,1) dapat dilihat pada Tabel 11.

Tabel 11. Estimasi Parameter Model GJR

Parameter	GJR(1,1)
	Inggris	Amerika
ω	0,001419	0,002843
α1	0,000000	0,153810
^l	0,995370	0,412784
Yi	0,081158	0,502348
AIC	-0,62629	-1,6772

Sumber : Data diolah (2019)

Setelah mendapatkan model, perlu dilakukannya pengujian efek autokorelasi pada residual model, guna mengetahui keefektifan model dalam mengakomadasi keberadaan autokorelasi. Berdasarkan Tabel 11. р-value uji Ljung-Box masing-masing residual model lebih besar dari taraf signifikan a = 0,05, sehingga tidak cukup bukti tolak hipotesis nol. Hal ini mengindikasikan adanya efek autokorelasi pada residual model.

Meramalkan Volatilitas Dengan Model Terbaik

Peramalan volatilitas dilakukan dengan sampel data kunjungan wisatawan Inggris dan Amerika bulan Januari 2010 sampai Desember 2018. Peramalan volatilitas data kunjungan wisatawan Inggris dan Amerika menggunakan model GARCH(1,1) dan GJR(1,1).

Tabel 12. Peramalan Volatilitas GARCH dan GJR Wisatawan Inggris

GARCH(1,1)
Peramal an	Sept 2018	Okt 2018	Nov 2018	Des 2018
	0,17748 37	0,17748 47	0,17748 56	0,17748 65
GJR(1,1)
Peramal	Sept 2018	Okt 2018	Nov 2018	Des 2018
an	0,16977 95	0,17352 43	0,17717 3	0,18073 18

Sumber: Data diolah (2019)

Tabel 12. menunjukan hasil peramalan volatilitas kunjungan wisatawan Inggris yang diestimasi menggunakan model GARCH(1,1)

pada bulan September 2018 sampai Desember 2018 mengalami peningkatan setiap bulannya. Hal serupa juga terlihat pada hasil peramalan volatilitas menggunakan model GJR(1,1).

Tabel 13. Peramalan Volatilitas GARCH dan GJR Wisatawan Amerika

GARCH(1,1)
Perama lan	Sept 2018	Okt 2018	Nov 2018	Des 2018
	0,8668 534	0,08133 8	0,07193 892	0,071 58736
GJR(1,1)
Perama	Sept 2018	Okt 2018	Nov 2018	Des 2018
lan	0,8405 429	0,07876 636	0,07374 277	0,073 79878

Sumber: Data diolah (2019)

Tabel 13. menunjukan hasil peramalan volatilitas kunjungan wisatawan Amerika yang diestimasi menggunakan model GARCH(1,1) pada bulan September 2018 sampai Desember 2018 mengalami penurunan setiap bulannya. Sedangkan hasil peramalan volatilitas kunjungan Amerika yang diestimasi menggunakan model GJR(1,1) mengalami penurunan pada bulan September 2018 sampai November 2018 kemudian mengalami peningkatan pada bulan Desember 2018.

Perhitungan VaR

Value at Risk kunjungan wisatawan Inggris dan Amerika ke Bali dapat diestimasi dengan metode parametrik seperti pada persamaan (9) dibantu dengan menggunakan software R. Berdasarkan hasil peramalan menggunakan metode rolling window diperoleh nilai VaR dengan tingkat kepercayaan 95% yang diberikan pada Tabel 12 dan 13:

Tabel 14. Estimasi VaR Model GARCH dan GJR Wisatawan Inggris

GARCH(1,1)
Va R	Tingkat Kepercayaan 95%
	Sept 2018	Okt 2018	Nov 2018	Des 2018
	- 69,2178 %	- 69,2180 %	- 69,2182 %	- 69,218 4%
GJR(1,1)
Va R	Tingkat Kepercayaan 95%
	Sept 2018	Okt 2018	Nov 2018	Des 2018
	-67,2%	-67,9%	-68,6%	-69,3%

Sumber : Data diolah (2019)

Tabel 14 dan Tabel 15 menunjukan

ambang VaR yang diprediksi pada tingkat kepercayaan 95% mewakili tingkat pertumbuhan terendah kunjungan wisatawan Inggris dan Amerika ke Bali. Dari hasil estimasi terlihat bahwa VaR dengan tingkat kepercayaan 95% kunjungan wisatawan Inggris dan Amerika yang diestimasi menggunakan model GARCH(1,1) pada bulan Desember 2018 yaitu -69,2184% dan -43,6% dengan rata-rata nilai VaR sebesar -56,4%. Hal ini berarti, jika Pemerintah Provinsi Bali menargetkan jumlah kunjungan sebesar 7.100.000 orang dengan biaya promosi yang dikeluarkan sebesar Rp. 134,1 per-orang. maka paling sedikit terdapat jumlah kunjungan sebesar 4.004.400 orang yang berwisata ke Bali. Sehingga biaya investasi yang dikeluarkan Pemerintah Provinsi Bali untuk promosi pariwisata sebesar Rp. 536.990.040.

Tabel 15. Estimasi VaR Model GARCH dan GJR Wisatawan Amerika

GARCH(1,1)
VaR	Tingkat Kepercayaan 95%
	Sept 2018	Okt 2018	Nov 2018	Des 2018
	-48,1%	-46,6%	-43,8%	-43,6%
GJR(1,1)
VaR	Tingkat Kepercayaan 95%
	Sept 2018	Okt 2018	Nov 2018	Des 2018
	-47,7%	-46,1%	-44,6%	-44,7%

Sumber : Data diolah (2019)

Tabel 15 menunjukan VaR dengan tingkat kepercayaan 95% kunjungan wisatawan Inggris dan Amerika yang diestimasi model GJR(1,1) pada bulan Desember 2018 yaitu --69,3% dan -44,7% dengan rata-rata nilai VaR sebesar -57%. Hal ini berarti, jika Pemerintah Provinsi Bali menargetkan jumlah kunjungan sebesar 7.100.000 orang dengan biaya promosi yang dikeluarkan sebesar Rp. 134,1 per-orang. maka paling sedikit terdapat jumlah kunjungan sebesar 4.047.000 orang yang berwisata ke Bali. Sehingga biaya investasi yang dikeluarkan Pemerintah Provinsi Bali untuk promosi pariwisata sebesar Rp. 542.702.700.

• 4.    KESIMPULAN DAN SARAN

Kesimpulan

Berdasarkan pembahasan yang diuraikan pada bab sebelumnya, diperoleh kesimpulan bahwa nilai estimasi VaR dengan tingkat kepercayaan 95% menggunakan model GARCH(1,1) wisatawan Inggris dan Amerika

pada bulan Desember 2018 secara berurutan sebesar -69,2184% dan -43,6% dengan rata-rata nilai VaR sebesar -56,4%. Hal ini berarti jika Pemerintah Provinsi Bali menargetkan jumlah kunjungan wisatawan sebesar 7.100.000 orang dengan biaya promosi pariwisata sebesar Rp.134,1 per-orang maka paling sedikit terdapat jumlah kunjungan sebesar 4.004.400 orang yang berwisata ke Bali. Sehingga biaya investasi yang dikeluarkan Pemerintah Provinsi Bali untuk promosi pariwisata sebesar Rp. 536.990.040.

Sedangkan nilai estimasi VaR dengan tingkat kepercayaan 95% menggunakan model GJR(1,1) wisatawan Inggris dan Amerika pada bulan Desember 2018 secara berurutan sebesar yaitu -69,3% dan -44,7% dengan rata-rata nilai VaR sebesar -57%. Hal ini berarti, jika Pemerintah Provinsi Bali menargetkan jumlah kunjungan sebesar 7.100.000 orang dengan biaya promosi yang dikeluarkan sebesar Rp. 134,1 per-orang paling sedikit terdapat jumlah kunjungan sebesar 4.047.000 orang yang berwisata ke Bali. Sehingga biaya investasi yang dikeluarkan Pemerintah Provinsi Bali untuk promosi pariwisata sebesar Rp. 542.702.700.

Saran

• 1.    Penelitian dapat dikembangkan dengan menggunakan data kunjungan pariwisata yang berbeda

• 2.    Hasil estimasi VaR dapat dikembangkan untuk memperkirakan pajak pariwisata

DAFTAR PUSTAKA

Bunnag, R., Chaitip, P. & Sriwichailamphan, T., 2010. Value at Risk of International Tourist Arrivals to Thailand. The Thailand Econometrics Society, II(2), pp. 332 - 352.

Danielsson, J.,   2001. Financial Risk

Forecasting: The Theory and Practice of Forecasting Market Risk with Implementation in R and Matlab. Chichester: John Wiley & Sons, Ltd.

Tsay, R. S., 2002. Analysis of Financial Time Series Financial Econometrics. Chicago: John Wiley & Sons, Inc.

Wei, W. W., 2006. Time Series Analysis

Univariate and Multivariate Methods. 2nd ed. United States: Pearson Education, Inc.

78