OPTIMASI PENDISTRIBUSIAN PRODUK MENGGUNAKAN MODEL FUZZY MULTIOBJEKTIF CYCLICAL INVENTORY ROUTING PROBLEM

Written by EKA SUSANTI, INDRAWATI INDRAWATI, ROBINSON SITEPU, ANNISA NABILA, RISKA WULANDARI
on January 31, 2020

E-Jurnal Matematika Vol. 9(1), Januari 2020, pp.96-103

DOI: https://doi.org/10.24843/MTK.2020.v09.i01.p285

ISSN: 2303-1751

OPTIMASI PENDISTRIBUSIAN PRODUK MENGGUNAKAN MODEL FUZZY MULTIOBJEKTIF CYCLICAL INVENTORY ROUTING PROBLEM

Eka Susanti^1§, Indrawati², Robinson Sitepu³, Annisa Nabila⁴, Riska Wulandari⁵

¹Jurusan Matematika, Fakultas MIPA, Universitas Sriwijaya [Email: eka susanti@mipa.unsri.ac.id] ²Jurusan Matematika, Fakultas MIPA, Universitas Sriwijaya [Email: iin10juni@yahoo.com] ³Jurusan Matematika, Fakultas MIPA, Universitas Sriwijaya [Email:robinson.sitepu@rocketmail.com] ⁴Jurusan Matematika, Fakultas MIPA, Universitas Sriwijaya [aniisanbl@gmail.com]
⁵Jurusan Matematika, Fakultas MIPA, Universitas Sriwijaya [riskawlndr07@gmail.com] ^§Corresponding Author

ABSTRACT

In distribution activities, travel time is influenced by several factors, such as vehicle conditions, traffic conditions and road conditions. Uncertain traffic conditions cause the travel time can not be defined with certainty (uncertain). If several variables are in a uncertain condition then a deterministic approach is not appropriate. Fuzzy approach, can be used to overcome uncertainty conditions. In this study, the optimal route for chicken egg delivery using the fuzzy Multiobjective Cyclical Inventory Routing Problem (FMOCIRP) model with time and cost is expressed by triangular fuzzy numbers. Model completion using Winqsb software. An optimal shipping route is obtained with a total cost of Rp 114,000 and a total delivery time of 132 minutes. The first optimal delivery route is distributor, retailer 1, retailer 2, retailer 3 and back to the distributor. The second route is distributor, retailer 5, retailer 4 and back to the distributor.

Keywords: Optimization, Fuzzy, Multiobjective

1. PENDAHULUAN

Inventory Routing Problem (IRP) adalah permasalahan inventory dimana supplier bertanggung jawab untuk mengkoordinasi penambahan persediaan pengecer dan rute kendaraan dalam proses pendistribusian. IRP merupakan penggabungan antara beberapa komponen yaitu inventory/persediaan dan perutean kendaraan yang akan dicapai secara simultan. Penelitian terkait permasalahan IRP telah banyak dilakukan dan diaplikasikan ke berbagai bidang. Permasalahan multi depot IRP dan penyelesaian model IRP dengan metode Branch and Cut telah dibahas oleh (Guimaraes et al. 2019). Permasalahan IRP dengan multi depot juga telah dibahas oleh (Bertazzi et al. 2019). Permasalahan IRP dengan kendala dalam kondisi deterministik telah dibahas oleh (Christos, Jose, and Pinto 2017). Permasalahan IRP untuk distribusi produk yang perishable (mudah rusak) telah dibahas oleh (Azadeh et al. 2017) dan (Hu, Toriello, and Dessouky 2018). Permasalahan IRP juga dikembangkan oleh (Chitsaz,

Divsalar, and Vansteenwegen 2016) untuk pola distribusi cyclic, selanjutnya disebut model Cyclical Inventory Routing Problem (CIRP). Permasalahan IRP dengan multi vehicle diperkenalkan oleh (Santos, Satoru, and Simonetti 2016) dan (Soysal 2016).

Beberapa penelitian sebelumnya membahas permasalahan IRP dan CIRP dengan satu fungsi tujuan yaitu meminimumkan biaya distribusi. Pada beberapa kasus, permasalahan IRP menginginkan lebih dari satu tujuan. Model Multiobjective Green Cyclical Inventory Routing Problem (MOGCIRP) dengan mempertimbangkan biaya dan total emisi kendaraan sebagai fungsi tujuan diperkenalkan oleh (Rau, Daniel, and Agus 2018). Beberapa metode untuk menyelesaikan permasalahan multiobjektif telah banyak dikembangkan, diantaranya (Liang et al. 2018) memperkenalkan algoritma hybrid bat dengan mempertimbangkan faktor ekonomi dan emisi.

Pada kegiatan distribusi, waktu tempuh dipengaruhi oleh beberapa faktor, seperti kondisi kendaraan, kondisi lalu lintas dan kondisi jalan. Kondisi lalu lintas yang tidak menentu mengakibatkan waktu tempuh tidak dapat didefinisikan dengan pasti (uncertain). Jika beberapa variabel dalam model dalam kondisi uncertain maka pendekatan deterministik tidak tepat digunakan. Pendekatan stokastik, pendekatan fuzzy, pendekatan Robust dan pendekatan probabilistik dapat digunakan untuk mengatasi kondisi uncertainty. Berikut diberikan

beberapa penelitian terkait kondisi uncertainty. Optimasi stokastik untuk permasalahan inventory perishable product dibahas oleh (Azadi et al. 2019), (Hu et al. 2019) menggunakan pendekatan fuzzy untuk permasalahan multiobjektif, (Liu and Dong 2018) menggunakan pendekatan robust untuk permasalahan multiobjective thermal system power plant, (Rahimi, Baboli, and Rekik 2017) menggunakan pendekatan stokastik untuk permasalahan multiobjektif, (Nikzad, Bashiri, and Oliveira 2018) membahas pendekatan stokastik pada permasalahan distribusi obat menggunakan model IRP under uncertainty, (Palacios et al. 2017) menggunakan pendekatan robust untuk menyelesaikan permasalahan multiobjektif pada penyusunan jadwal pekerja took, (Susanti, Dwipurwani, and Yuliza 2017) menggunakan pendekatan fuzzy pada permasalahan pengangkutan sampah.

Penelitian ini mengimplementasikan model FMOCIRP pada distribusi telur ayam dengan biaya dan waktu dinyatakan dengan bilangan fuzzy. Bilangan fuzzy yang digunakan adalah Triangular Fuzzy Number (TFN). Model FMOCIRP merupakan pengembangan model IRP dan permasalahan multiobjektif yang telah dibahas pada penelitian (Rau et al. 2018). Akan tetapi pada penelitian ini fungsi tujuan yaitu fungsi waktu dan fungsi biaya dinyatakan dengan TFN. Berikut diberikan model FMOCIRP dengan dua fungsi tujuan.

Diberikan fungsi tujuan

min ⁼ (Fungsi biaya)

min ^2 ⁼ (Fungsi total emisi)

Fungsi kendala :(1)

^∑k∈O^∑I∈V_k ^∑i∈Vki ^xklij =1; ∀j,j∈S

^xklcj≤1; ∀{k,l,j}, j∈S․l∈

^xklic≤1; ∀{k,l,i}, i∈S․l∈

^∑k∈O^∑l∈V_k ^∑i∈Vki ^xklij ^-

∑k∈O∑l∈V_k ∑m∈Pki ^kljm=0;∀j,j∈S

^∑k∈O ∑( I∈V_kI∈V_k) ^zkij ^-

^∑k∈O ∑( l∈Vkl∈V_k)

⅛ ×∑k∈O^∑l∈V_k ^∑i∈V_kι ^xklij;∀j∈S γmm ≤ Ct_k ≤ Tff^ax;∀ k∈O

Qki =∑i∈V_ki ^zkcj;∀ {k,l }, k∈O,l∈ Pk

{^xklij, Vk} ∈{0,1};∀{k,l,i,j },

{i,j}∈S,k∈O,l∈ Pk

{Ctk, ^zkij}≥0;∀{k,i,j},{i,j}∈S,

k∈O,l∈ Pk

dengan

^xklij' variabel keputusan rute dari titik i ke titik j

C pusat distribusi

S himpunan titik sales

O cyclic tour , O ={Pl ⋯ ⋯ }

Pk single tour

Pk ={C, S ci , ^sb,⋯,$1,C }, ^i ∈s , atau =

^{Pkl ^⋯ }

Pkl ={C^, ^a ^,^sb,⋯,St^,C }, ^i ^∈s⊂ Pkl

qj kuantitas penambahan produk untuk

setiap titik j

Ctk waktu siklus

Tff^m minimum waktu siklus untuk setiap k

Tff^ax maksimum waktu siklus untuk setiap k ^cIkl kuantitas produk yang diangkut pada

subtour l di cyclic tour k

^zklj tingkat produk yang diangkut oleh

kendaraan k ketika perjalanan dari titik i ke titik j

D_ij Jarak titik i ke titik j

AS kecepatan rata-rata kendaraan

DR_i tingkat permintaan titik i

UT Biaya pengiriman rata-rata

VC kapasitas maksimum kendaraan

_τmιn =∑i∈V_k ^∑J∈V_k ( ^dU ^/ AS)/(1-

2∑i∈V_kDRi/ UT)

Tff^ax = /∑i∈V_kl∈V_kDRi

Tff^ax = { γmax ⋯ }

2. METODE PENELITIAN

Berikut diberikan langkah-langkah penyelesaian permasalahan optimasi

pendistribusian menggunakan model

FMOCIRP

1. Pengumpulan Data.

Data yang digunakan dalam penelitian ini adalah data primer. Terdiri dari data jumlah pengecer, banyak permintaan rata-

rata pengecer perhari, biaya dan waktu pengiriman.

2. Pengembangan Model Fuzzy

Multiobjektive Inventory Routing Problem (FMOCIRP). Model FMOCIRP

merupakan pengembangan model yang MOGCIRP yang diperkenalkan oleh (Rau et al. 2018). Pada (Rau et al. 2018) nilai parameter diketahui dengan pasti atau bersifat deterministik. Pada penelitian ini parameter biaya dan waktu

dipertimbangkan dalam kondisi

ketidakpastian dan dinyatakan dalam bentuk bilangan fuzzy. Berikut diberikan fungsi tujuan model FMOCIRP.

Diberikan fungsi tujuan

min Z^ = ̃ ^xklij' (Fungsi biaya) (2) min ^2 = ̃ ^xklij' (Fungsi waktu) Kendala model FMOCIRP yang digunakan analog dengan model MOGCIRP

3. Mentransformasi model FMOCIRP (2) ke bentuk deterministik

Langkah-langkah penyelesaian adalah sebagai berikut

a. Menentukan penyelesaian single objektif Zy dan ^2 masing-masing diperoleh solusi { *1¹ , X₁² } dan { ¾¹ , X₂² }
b. Menentukan nilai target untuk ^l dan ¾ , yaitu

⁼

min { ^zk (⅛ ), ^zk ( ¾² ), ^zk ( ^¹), ^zk ( ¾² )}

,k=1,2

=

max { ^zk (⅛ ), ^zk ( ^²), ^zk (⅛ ), ^zk (*1 )} ,k=1,2

Diperoleh bentuk deterministik model (2), yaitu

maks λ

Kendala

λ<h⁽^χ⁾-Ui

^- L₁-U₁

λ_<h⁽^x⁾-U₂

(3)

^∑k∈O^∑I∈V_k ^∑i∈Pki ^xklij=1; ∀j,j∈S

^xklcj≤1; ∀{k,l,j }, j∈S,l∈ Pk,k∈O

^xklic≤1; ∀{k,l,i}, i∈S,l∈ , ∈O

^∑k∈O^∑l∈P_k ^∑i∈p_ki ^xklij ^-

^∑k∈O^∑l∈P_k ^∑m∈Pki ^xkljm=0;∀j,j∈S

^∑k∈O ∑( I∈P_kι∈P_k) ^zkij ^-∑k∈O ∑( l∈P_kι∈P_k) ⁼

Qj ×∑k∈O^∑l∈P_k ^∑i∈p_kι ^xklij;∀j∈S γmιn ≤ Ctk ≤ Tg^lax;∀ k∈O

Qki =∑i∈P_ki ^zkcj;∀ {k,l }, k∈O,l∈ Pk {^xkllj, Vk}∈;∀{k,l,i,j},{i,j}∈S, k∈O,l∈ Pk {Ctj_i, ^zkij}≥0;∀{k,i,j},{i,j}∈ S,

k∈O,l∈ Pk

Penyelesaian Model (3) menggunakan software Winqsb.

3. HASIL DAN PEMBAHASAN

Pada makalah ini ditentukan rute optimal pengiriman telur ayam dari distributor ke lima pengecer dengan mempertimbangkan biaya dan waktu pengiriman, permintaan pengecer dan kapasitas maksimal kendaraan. Fungsi tujuan Zy adalah fungsi yang meminimunkan total biaya pengiriman. Koefisien dari variabel ^xklij' adalah TFN untuk biaya pengiriman dari titik i ke titik j. Fungsi tujuan Z^ adalah fungsi yang meminimumkan total waktu pengiriman. Waktu pengiriman terdiri dari waktu tempuh dan waktu loading. Biaya pengiriman rata-rata persiklus tour (UT) sebesar Rp.59.000, kecepatan rata kendaraan 40 km/jam. Permintaan rata-rata di titik 1 sampai dengan 5 berturut-turut sebagai berikut, 60 kg, 60 kg, 45 kg, 90 kg, 45 kg. Bahan bakar yang digunakan kendaraan adalah bensin. Biaya dalam satuan rupiah dan waktu dengan satuan menit. Diasumsikan bahwa rute dapat dilalui bolak balik atau jalur dua arah. Kapasitas maksimal kendaraan adalah 170 kg.

Mempertimbangkan kapasitas maksimal kendaraan, dibentuk dua wilayah pengiriman, yaitu tour 1 dan tour 2 ( l = 1,2) menggunakan satu jenis kendaraan (k=1) atau dapat dituliskan Pkl ={Pii, P12 }, dimana = {C, Ul, U₂ , U₃,C}, P12 ={C, U₄ , Us ,C}. Titik c adalah pusat distribusi, selanjutnya disebut depot. Pembagian wilayah pengiriman diberikan pada Gambar 1 berikut.

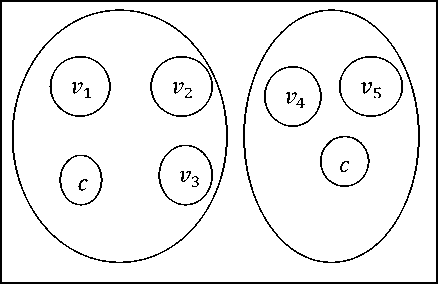
Gambar 1. Pembagian Wilayah Pengiriman

, . . . . . . .. .

(1000; 1000; 6000)^xllv5v4 +

. . . . . . . . ..

(1000; 1000; 6000)^x12v5v4 +

(30000; 30000; 35000)¾1CV5 +

(30000; 30000; 35000)^x12cv3 +

, . . . . . . .. .

(1000; 1000; 6000)^xllv4v5 +

. . . . . . . . ..

(1000; 1000; 6000)^x12v4v5 +

(26000;2^̃6000;31000)^xllv4c +

(26000;2^̃6000;31000)¾2v4c +

(30000; 30000; 35000)^xllv5c +

(30000;3^̃0000;35000) (4)

Menggunakan model FMOCIRP, ditentukan rute pengiriman berdasarkan pembagian wilayah pada Gambar 1. Berikut diberikan formulasi model FMOCIRP.

=

(20000;2^̃0000;25000)¾icvi + (20000;2^̃0000;25000)⅛cvi +

(4000; 4000; 9000) ¾W2vl + (4000;4^̃000;9000)¾2u2ul + (8500; 8500; 13500) ¾lv3vl + (8500;8^̃500;13500)¾2V3V1 + (25000;2^̃5000;30000)¾1CV2 + (25000; 25000; 30000)^x12cv2 + (4000;4^̃000;90000)¾1V1V2 + (4000;4^̃000;9000)^x12vlv2 + (4500;4^̃500;9500)^xllv3v2 + (4500;4^̃500;9500)^x12v3v2 + (28500;2^̃8500;33500)^xllCV3 + (28500;2^̃8500;33500)¾2CV3 + (8500;8^̃500;13500)¾1V1V3 + (8500;8500;13500)¾2vlu3 + (4500;4^̃500;9500)^xllv2v3 + (4500;4^̃500;9500)^x12v2v3 + (20000; 20000; 25000)¾ivic + (20000;2^̃0000;25000)^xιivic + (25000; 25000; 30000)^xllv2c + (25000; 25000; 30000)^x12v2c + (28500; 28500; 33500)^xllv3c + (28500;2^̃8500;33500)¾2v3c + (26000; 26000; 31000)¾1CV4 + (26000;2^̃6000;31000)¾2CV4 +

Min Z₂ =(20;20;25)^xιicvi + (20;^̃20;25)^x12cvi+(8;^̃8;13)^xllv2vl + (8;^̃8;13)¾2v2ul + (15;^̃15; 20) ¾W3V1 + (15;^̃15;20) ¾2V3V1 +(24;^̃24;29) ¾1CV2 + (24;^̃24;29)^x12cv2+(8;^̃8;13) ¾1V1V2 + (8;^̃8;13)^x12vlv2 + (9;^̃9; 14)^xllv3v2 + (9;^̃9;14)^x12v3v2+(37;^̃37;42)^X11CV3 + (37;^̃37;42)^x12cv3+(15;^̃15;20) ¾1V1V3 + (15;^̃15;20) ¾2vlu3 + (9;^̃9; 14)¾W2u3 + (9;^̃9;14)¾2v2u3 +(20;^̃20;25)^xIivic + (20;^̃20;25)XllVlC+(24;^̃24;29)^xllv2c + (24;^̃24;29)^x12v2c + (37;^̃37; 42)Xllv3c + (37;^̃37; 42)^x12v3c+(26;^̃26;31)^xιicvⁱi +

----.

(26;26;31)¾2CV4 +(4;4;9)^xllv3v4 +

----.

——■—

(4;4;9)^x12v3vl+(28;28;33)^X11CV3 +

——■—

----.

(28;28;33)¾2cv5 +(4;4;9)^xllv4v3 +

----.

(4;4;9)^x12v4v3+(26;26;31) ¾1V4C +

λ . i - - i

(26; 26; 31)¾2v4c + ¾2CV4 +

----.

(4;4;9)^xllv3v4+(4;4;9)^x12v3v4 +

(28; 28; 33)¾1CV5 + ¾lv5c + ¾2CV4 +

----.

(4;4;9)^xllv3v4+(4;4;9)^x12v3v4 +

(28; 28; 33)^xllcv3 + ^x12v5c

Kendala

^xIicvi + ^x12cvl + ^xllv2vl + ^x12v2vl +

^xllv3vl ⁺^x12v3vl=1

^xllcv2 + ^x12cv2 + ^xllvlv2 + ^x12vlv2 +

^xllv3v2 + ^x12v3v2=1

¾1CV3 + ¾2cv3 + ¾1V1V3 + ^x12vlv3 +

¾1V2V3 ⁺ ¾2v2u3 =1

¾1CV4 + ¾2CV4 + ¾lv5v4 + ^x12v5v4=1

¾1CV5 + ¾2cv5 + ¾1V4V5 + ¾2v4v5 =1

^xIlCVl ⁺^X12CV1 ⁺^xllcv2 ⁺^x12cv2 ⁺^xllCV3 ⁺

^x12cv3 =1

^xllv2vl + ^x12v2vl + ^xllvlv2 + ^x12vlv2 + ^xllvlv3 + ^x12vlv3 =1

^xllv3vl + ^x12v3vl + ^xllv3v2 + ^x12v3v2 +

^xllv2v3 ⁺^x12v2v3 =1

^xllCV4 + ^x12cv4 + ^xIlCVS + ^x12cv3=1

^xllvSv4 + ^x12vSv4 + ^xllv4vS + ^x12v4vS=1

^xιicvi≤1 ;^x12cvl≤1;^xllcv2≤1;^x12cv2 ^≤1; ^xllCV3≤1;^x12cv3≤1

^xllcv4≤1;^x12cv4≤1;^xllcv5≤1 ;^x12cvS ≤ 1

^xιivic≤1;^x12vlc≤1;^xllv2c≤1;^x12v2c ^≤1; ^xllv3c≤1;^x12v3c≤1

^xllv4c≤1;^x12v4c≤1;^xllv5c≤1;^x12vSc ≤ 1

1; ^xιicvS=1;^xllv4c; ^zicvi = 3600; ⁼

3600; ^zicv3 = 2025; ^zlcv4 = 8100; ⁼

2025}. Nilai X2 (X^) =126,X2 ( xl)=

161, X2 ( Xl) =132, Z2 ( Xl ) =167 dengan

X2 = ={^xιicvi=1; ⁼

1; ^xllvlv3=1;^xllv2c=1;

1; ^xιicvS=1;^xllv4c=1 ;

3600; ^zlcv2 = 3600; ^zicv3 = 2025;

8100; ^zIcvS = 2025}. Nilai = 150000 ;

L1 = 114000; Ui=126 ; Li = 167. Dapat dibentuk model deterministik dari

Permasalahan (4) adalah sebagai berikut.

Maks λ

^xιicvi + ^x12cvl + ^xllv2vl + ^x12v2vl + ^xllv3vl ⁺^x12v3vl - ^xIivic - ^x12vlc -^xllvlv2 - ^x12vlv2 - ^xllvlv3 - ^x12vlv3 =0 ^xllcv2 + ^x12cv2 + ^xllvlv2 + ^x12vlv2 + ^xllv3v2 ⁺^x12v3v2 - ^xllv2c - ^x12v2c -^xllv2vl - ^x12v2vl - ^xllv2v3 - ^x12v2v3 =0 ^xllCV3 + ^x12cv3 + ^xllvlv3 + ^x12vlv3 + ^xllv2v3 + ^x12v2v3 - ^xιiv3c - ^x12v3c -^xllv3vl - ^x12v3vl - ^xllv3v2 - ^x12v3v2 =0

Kendala

^xllCV3 + ^x12cv3 + ^xllVlv3 + ^x12vlv3 +

^xllv2v3 + ^x12v2v3

_-

^xιiv3c

_-

^x12v3c

_-

^xιiv3vi

_-

^x12v3vl

_-

^xllv3v2

_-

^x12v3v2 =0

^xllcv4 + ^x12cv4 + ^xllv5v4 + ^x12vSv4

_-

^xllv4c

_-

^x12v4c

_-

^xllv4v5

_-

^x12v4vS =0

^xllCVS + ^x12cv5 + ^xllv4vS + ^x12v4vS

_-

^xιiv5c

_-

^x12v5c

_-

^xllvSv4

_-

^x12v5v4=0

^zicvi + ^zlv2vl + ^zlv3vl

_-

^zivic

_-

^zlvlv2

_-

^zlvlv3 = (60) (^xιicvi + ^x12cvl + ^xllv2vl + ^x12v2vl + ^xllv3vl + ^x12v3vl)

^zlcv2 + ^zlvlv2 + ^zlv3v2

_-

^zlv2c

_-

^zlv2vl

_-

^zlv2v3 = (60)²⁽^xllcv2 + ^x12cv2 + ^xllvlv2 + ^x12vlv2 + ^xllv3v2 + ^x12v3v2)

20000^xιicvi + 20000^x12cvi + 4000^xllv2vl + 4000^x12v2vl +

8500^xllv3vl + 8500^x12v3vl +

25000X ^{+ 25000}X ⁺

4000^xllvlv2 + 4000^x12vlv2 + 4500^xllv3v2 + 4500^x12v3v2 +

28500^xllCV3 + +28500^x12cv3 +

8500^xllVlv3 + 8500^x12vlv3 + 4500^xllv2v3 + 4500^x12v2v3 + 20000^xιivic + 20000^xIivic + 25000^xllv2c + 25000^x12v2c + 28500^xllv3c + 28500^x12v3c + 26000^xIlcv 4 + 26000^x12cv4 + 1000^xllvSv4 + 1000^x12vSv4 + 30000^xιicvS + 30000^x12cvS +

1000^xllv4vS + 1000^x12v4vS + 26000^xllv4c + 26000^x12v4c +

30000^xιivSc + 30000^x12vSc + 36000λ≤ 150000

^zicv3 + ^zlvlv3 + ^zlv2v3

_-

^ziv3c

_-

^zlv3vl

_-

^zlv3v2 = (45)²⁽^xllCV3 + ^x12cv3 + ^xllvlv3 + ^x12vlv3 + ^xllv2v3 + ^x12v2v3)

^zlcv4 + ^zlv5v4

_-

^zlv4c

_-

⁼

(90)²(^xllcv4 + ^x12cv4 + ^xllv5v4 + ^x12vSv4)

^zlCV 5 + ^zlv4vS

_-

^zIvSc

_-

⁼

20^xιicvi+20^x12cvl+8^xllv2vl + 8^x12v2vl+15^xllv3vl+15^x12v3vl + 24^xllcv2 +24^x12cv2 +8^xllvlv2 + ⁸^x12vlv2 +9^xllv3v2 +9^x12v3v2 + 37^xllCV3 ++37^x12cv3+15^xllvlv3 + 15^x12vlv3 +9^xllv2v3 +9^x12v2v3 +

(45)²(^xIicvS + ^x12cvS + ^xllv4vS + ^x12v4vS)

180≤Ct₁ ≤222

^zicvi + ^zlcv2 + ^zicv3 ≤ 9225

^zlcv4 + ^zIcvS ≤ 10125

^xklij ∈ {0,1} ; ^zkij, Ct₁ ≥0

Penyelesaian model (4) menggunakan

20^xιivic+20^xIivic+24^xllv2c + 24^x12v2c+37^xllv3c+37^x12v3c +

26^xllcv4+26^x12cv4+4^xllv5v4 +

4^x12vSv4+28^xιicvS+28^x12cvS +

4^xllv4vS+4^x12v4vS+26^xllv4c +

26^x12v4c+28^xιivSc+28^x12vSc+41λ≤ 167

software objektif adalah 149000, dengan

Winqsb, diperoleh solusi single untuk masing-masing nilai TFN

Z₁ ( Xi) = 114000, Xl ( Xl)=

^zI ( xl) =115,Xl ( Xl)=150

Xl = ={^xllv2vl=1; ⁼

1; ^xllCV3=1;^xIivic=1; ⁼

^xιicvi + ^x12cvl + ^xllv2vl + ^x12v2vl + ^xllv3vl ⁺^x12v3vl=1

^xllcv2 + ^x12cv2 + ^xllvlv2 + ^x12vlv2 +

^xllv3v2 + ^x12v3v2=1 (5)

^xllCV3 ⁺^x12cv3 ⁺^xllvlv3 ⁺^x12vlv3 ⁺^xllv2v3 ⁺^x12v2v3=1

^xllCV4 + ^x12cv4 + ^xllvSv4 + ^x12vSv4=1

¾1CV5 + ^x12cvS + ^xllv4vS + ¾2Hu5 =1 ¾1CV1 + ^x12cvl + ^xllCV2 + ^x12cv2 + ^xllCV3 +

^x12cv3=1

λ=1; ^xιicvi=1; ^xιiviv2^{; =}

1; ^xllv3c=1; ^xιicvs=1;

1; ^xllv4c=1;^zicvi = 3600;

3600; ^xllCV3 = 2025;

¾1V2V1 + ¾2v2vl + ¾1V1V2 + ^x12vlv2 + ¾1V1V3 + ¾2vlv3 =1

¾W3V1 + ^x12v3vl + ¾1V3V2 + ¾2v3v2 + ¾W2u3 ⁺ ¾2v2v3 =1

¾1CV4 + ^x12cv4 + ^xllCVS + ¾2cv5 =1 ¾1v5v4 + ^x12vSv4 + ^xllv4vS + ^x12v4vS=1 ¾1CV1≤1 ;^x12cvl≤1;^xllCV2≤1; ¾2cv2 ^≤1; ^xllcv3≤1;^x12cv3≤1

^xllCV4≤1;^x12cv4≤1;^xιicvs≤1 ;^x12cv5 ≤ 1

^xιivic≤1;^x12vlc≤1;^xllv2c≤1;^x12v2c ^≤1; ^xllv3c≤1;^x12v3c≤1

^xllv4c≤1;^x12v4c≤1;^xιiv5c≤1;^x12vSc ^≤1

^xιicvi + ^x12cvl + ^xllv2vl + ^x12v2vl + ^xllv3vl ⁺^x12v3vl - ^xIivic - ^x12vlc -^xllvlv2 - ^x12vlv2 - ^xllvlv3 - ^x12vlv3 =0 ^xllcv2 + ^x12cv2 + ^xllvlv2 + ^x12vlv2 + ^xllv3v2 ⁺^x12v3v2 - ^xllv2c - ^x12v2c -^xllv2vl - ^x12v2vl - ^xllv2v3 - ^x12v2v3 =0 ^xllCV3 + ^x12cv3 + ^xllvlv3 + ^x12vlv3 + ^xllv2v3 + ^x12v2v3 - ^xιiv3c - ^x12v3c -^xllv3vl - ^x12v3vl - ^xllv3v2 - ^x12v3v2 =0

8100; ^xιicvS = 2025

Total biaya Z₁ = 114000 ; total waktu pengiriman ^2 =132. Rute pengiriman optimal C→ V₁ → V₂ → V₃ →C dan C→ ^vS → V₄ →C . Total biaya untuk dua tour pengiriman sebesar Rp 114.000 dengan total waktu selama 132 menit.

Rute pengiriman untuk tour satu adalah distributor, pengecer 1, pengecer 2, pengecer 3 dan kembali lagi ke distributor. Rute pengiriman dua adalah distributor, pengecer 5, pengecer 4 dan kembali lagi ke distributor. Rute pengiriman yang dilakukan sebelumnya oleh distributor tidak tetap, total biaya rata-rata setiap tour sebesar Rp.59.000 atau sebesar Rp 118.000 untuk dua tour pengiriman. Menggunakan model FMOCIRP berdasarkan pembagian wilayah pada Gambar 1 diperoleh total biaya lebih minimum sebesar Rp 4.000 dibandingkan dengan tour yang dilakukan distributor sebelumnya.

^xllCV3 + ^x12cv3 + ^xllVlv3 + ^x12vlv3 + ^xllv2v3 + ^x12v2v3 - ^xιiv3c - ^x12v3c -^xιiv3vi - ^x12v3vl - ^xllv3v2 - ^x12v3v2 =0 ^xllCV4 + ^x12cv4 + ^xllv5v4 + ^x12v5v4 ^-^xllv4c - ^x12v4c - ^xllv4v5 - ^x12v4v5 =0 ^xllCVS + ^x12cvS + ^xllv4v5 + ^x12v4vS ^-^xιiv5c - ^x12vSc - ^xllv5v4 - ^x12v5v4=0

^zicvi + ^zlv2vl + ^zlv3vl ^-^zivic ^-^zlvlv2 ^-^zlvlv3 = (60) (^xιicvi + ^x12cvl + ^xllv2vl +

^x12v2vl + ^xllv3vl + ^x12v3vl⁾

^zlcv2 + ^zlvlv2 + ^zlv3v2

_-

^zlv2c

_-

^zlv2vl

_-

^zlv2v3 = (60)²⁽^xllcv2 + ^x12cv2 + ^xllvlv2 + ^x12vlv2 + ^xllv3v2 + ^x12v3v2)

^zicv3 + ^zlvlv3 + ^zlv2v3

_-

^ziv3c

_-

^zlv3vl

_-

^zlv3v2 = (45)²⁽^xllcv3 + ^x12cv3 + ^xllvlv3 + ¾2vW3 + ¾W2v3 + ^x12v2v3)

^zlcv4 + ^zlvSv4 - ^zlv4c - ⁼

(90)²(^xIlCV4

+ ^x12cv4 + ^xllv5v4 + ^x12vSv4⁾

^zIcvS ⁺^zlv4v5 - ^zIvSc - ⁼

(45)²(¾1CV5 + ^x12cvS + ^xllv4vS + ^x12v4vS)

180≤Ct₁ ≤222

^zicvi + ^zicv2 + ^zicv3

≤ 9225

^zlcv4 + ^zIcvS ≤ 10125

^xklij ∈ {0,1} ; ^zkij, Ct₁ ≥0 ;λ ∈ [0,1]

Penyelesaian model (5) menggunakan software Winqsb, diperoleh solusi sebagai berikut.

4. KESIMPULAN

Berdasarkan hasil dan pembahasan dapat disimpulkan bahwa :

1. Pendekatan fuzzy dapat digunakan untuk

penyelesaian model FMOCIRP pada permasalahan pendistribusian produk.

2. Pada permasalahan optimasi

pendistribusian telur dengan 5 depot diperoleh optimal waktu pengiriman selama 132 menit dan total biaya sebesar Rp 114000 dengan rute optimal C→ V₁ → V₂ → V₃ →C dan C→ ^vS → V₄ →C.

5. SARAN

Pada penelitian ini hanya

dipertimbangkan satu jenis kendaraan, untuk penelitian selanjutnya dapat dipertimbangkan beberapa jenis kendaraan dengan perbedaan kapasitas pengangkutan. Pada beberapa wilayah terdapat jalan dengan jalur satu arah, model yang dikembangkan pada penelitian ini mengasumsikan bahwa jalur yang dilalui adalah dua arah, untuk selanjutnya dapat ditambahkan beberapa kondisi pada model jika jalur yang dilalui adalah satu arah.

DAFTAR PUSTAKA

Azadeh, A., S. Elahi, M.Hosseinabadi Farahani, and B. Nasirian. 2017. “A Genetic Algorithm-Taguchi Based Approach for Inventory Routing Problem of a Single Perishable Product with Transshipment.” Computers & Industrial Engineering 104:124–33. Retrieved (http://dx.doi.org/10.1016/j.cie.2016.12.01 9).

Azadi, Zahra, Sandra D. Eksioglu, Burak Eksioglu, and Gokce Palak. 2019. “Stochastic Optimization Models for Joint Pricing and Inventory Replenishment of Perishable Products.” Computers & Industrial Engineering 127(January):625– 42. Retrieved

(https://doi.org/10.1016/j.cie.2018.11.004)

Bertazzi, Luca, Leandro C. Coelho, Annarita De Maio, and Demetrio Laganà. 2019. “A Matheuristic Algorithm for the MultiDepot Inventory Routing Problem.” Transportation Research Part E 122:524– 44. Retrieved

(https://doi.org/10.1016/j.tre.2019.01.005).

Chitsaz, Masoud, Ali Divsalar, and Pieter Vansteenwegen. 2016. “A Two Phase Algorithm For The Cyclic Inventory Routing Problem.” European Journal of Operational Research 254(2, 16 October 2016):410–26. Retrieved

(http://dx.doi.org/10.1016/j.ejor.2016.03.0 56).

Christos, Y. D. .., Maravelias Jose, and M. Pinto. 2017. “Solution Methods for Vehicle-Based Inventory Routing Problems.” Computers and Chemical Engineering 101(9 June 2017):259–78. Retrieved (http://dx.doi.org/10.1016/j.compchemeng. 2017.02.036).

Guimaraes, T. .., Leandro C. Coelho, M.Clede. Schenekemberg, and T. .. Scarpin. 2019. “The Two-Echelon Multi-Depot Inventory Routing Problem.” Computers and Operation Research 101(January

2019):220–33.

Hu, Chaofang, Zelong Zhang, Na Yang, Hyo S. Shin, and Antonios Tsourdos. 2019. “Fuzzy Multiobjective Cooperative Surveillance of Multiple UAVs Based on Distributed Predictive Control for

Unknown Ground Moving Target in Urban Environment Chaofang.”

Aerospace Science and Technology 84(January 2019):329–38. Retrieved (https://doi.org/10.1016/j.ast.2018.10.017).

Hu, Weihong, Alejandro Toriello, and Maged Dessouky. 2018. “Integrated Inventory Routing Problem and Freight Consolidation Perishable Goods.”

European Journal of Operational Research 271 (2, 1 December 2018):

548–60. Retrieved

(https://doi.org/10.1016/j.ejor.2018.05.034 )

Liang, Huijun, Yungang Liu, Fengzhong Li, and Yanjun Shen. 2018. “Electrical Power and Energy Systems A Multiobjective Hybrid Bat Algorithm for Combined Economic / Emission Dispatch.” Electrical Power and Energy Systems

101(March):103–15. Retrieved

(https://doi.org/10.1016/j.ijepes.2018.03.0 19).

Liu, Miao and Ze Dong. 2018. “Multiobjective Robust H 2 / H ∞ Fuzzy Tracking Control for Thermal System of Power Plant.” Journal of Process Control 70:47–64. Retrieved (https://doi.org/10.1016/j.jprocont.2018.08 .004).

Nikzad, Erfaneh, Mahdi Bashiri, and Fabricio Oliveira. 2018. “Two-Stage Stochastic Programming Approach For The Medical Drug Inventory Routing Problem Under Uncertainty.” Computers & Industrial Engineering 128:358–70. Retrieved (https://doi.org/10.1016/j.cie.2018.12.055)

Palacios, Juan José, Inés González-rodríguez, Camino R. Vela, and Jorge Puente. 2017. “Robust Multiobjective Optimisation For Fuzzy Job Shop Problems.” Applied Soft Computing Journal 56:604–16. Retrieved (http://dx.doi.org/10.1016/j.asoc.2016.07.0 04).

Rahimi, Mohammad, Armand Baboli, and Yacine Rekik. 2017. “Multi-Objective Inventory Routing Problem : A

Stochastic Model to Consider Profit , Service Level and Green Criteria.” Transportation Research Part E 101:59– 83. Retrieved

(http://dx.doi.org/10.1016/j.tre.2017.03.00 1).

Rau, Hsin, Syarif Daniel, and Gede Agus. 2018. “Optimization of the MultiObjective Green Cyclical Inventory Routing Problem Using Discrete MultiSwarm PSO Method.” Transportation Research Part E 120(October):51–75. Retrieved (https://doi.org/10.1016/j.tre.2018.10.006).

Santos, Edcarllos, Luiz Satoru, and Luidi Simonetti. 2016. “A Hybrid Heuristic Based on Iterated Local Search for Multivehicle Inventory Routing Problem.” Electronic Notes in Discrete Mathematics 52:197–204. Retrieved

(http://dx.doi.org/10.1016/j.endm.2016.03. 026).

Soysal, Mehmet. 2016. “Closed-Loop Inventory Routing Problem for Returnable Transport Items.” Transportation

Research Part D 48(December 2015):31– 45. Retrieved

(http://dx.doi.org/10.1016/j.trd.2016.07.00 1).

Susanti, Eka, Oki Dwipurwani, and Evi Yuliza. 2017. “Optimasi Kendaraan Pengangkut Sampah Menggunakan Model Fuzzy Goal Programming.” Jurnal Matematika 7(2):119–23.

103

OPTIMASI PENDISTRIBUSIAN PRODUK MENGGUNAKAN MODEL FUZZY MULTIOBJEKTIF CYCLICAL INVENTORY ROUTING PROBLEM

OPTIMASI PENDISTRIBUSIAN PRODUK MENGGUNAKAN MODEL FUZZY MULTIOBJEKTIF CYCLICAL INVENTORY ROUTING PROBLEM

1. PENDAHULUAN

2. METODE PENELITIAN

3. HASIL DAN PEMBAHASAN

DAFTAR PUSTAKA

Discussion and feedback