MENENTUKAN SAHAM YANG EFISIEN DENGAN MENGGUNAKAN METODE CAPITAL ASSET PRICING MODEL (CAPM)
on
E-Jurnal Matematika Vol. 9(1), Januari 2020, pp.23-30
DOI: https://doi.org/10.24843/MTK.2020.v09.i01.p274
ISSN: 2303-1751
MENENTUKAN SAHAM YANG EFISIEN DENGAN MENGGUNAKAN METODE CAPITAL ASSET PRICING MODEL (CAPM)
Elvina Liadi1§, Komang Dharmawan2, Desak Putu Eka Nilakusmawati3
1Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: elvinaliadi91@gmail.com]
2Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: dharmawan.komang@gmail.com.]
3Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: nilakusmawati@unud.ac.id]
§Corresponding Author
ABSTRACT
CAPM has been well known as a method to select which stocks are efficient in a portfolio. The purpose of this study is to determine efficient stocks using CAPM method. Data used in this study are the monthly closing prices recorded from February 2016 to July 2018. The results of this study indicate that the CAPM is able to show efficient stocks with differences in the return and expected return of a positive or negative value of CAPM. In this study, it is found that AMAG.JK, ASBI.JK, ASJT.JK, ASMI.JK, ASRM.JK, PNIN.JK, VINS.JK, LPGI.JK, MREI.JK are efficient stocks while ABDA.JK, AHAP.JK, ASDM.JK are inefficient stocks
Keywords: Systematic risk, Expected Return, CAPM, Inefficient Stocks, Efficient Stocks
Sektor keuangan merupakan salah satu sektor pendorong iklim investasi di Indonesia. Hal tersebut ditunjukkan dari bidang investasi yang semakin mengalami perubahan positif. Perubahan positif ditunjukkan dari peningkatan transaksi yang dilakukan investor pada pasar modal.
Investor memanfaatkan tempat wadah pertemuan antara menyediakan dana dan investor dan pasar modal untuk memperoleh capital gain dan dividend. Selain itu, indikator ekonomi biasanya dilihat dari perkembangan pasar modal.
Selain dana tidak hanya mempertimbangkan investasi tetapi juga hal-hal sebagai berikut : tingkat pengembalian yang diharapkan (expected rate of return) dan juga tingkat risiko (rate of risk) (Tandelilin, 2010:11). Risiko adalah suatu selisih antara hasil yang akan datang dan hasil secara nyata (Zubir, 2010:19). Tingkat suatu risiko ditentukan dari besarnya penyimpangan yang terjadi.
Teori portofolio berkaitan berhubungan teori peramalan pada risiko dan tingkat pengembalian dengan cara membentuk aset dalam berbagai kombinasi yang istilahkan diversifikasi. Portofolio efisien merupakan
suatu portofolio yang mampu menghasilkan suatu keuntungan (return) di atas nilai risiko yang ditentukan.
Berdasarkan teori tersebut, maka perlu dipertimbangkan cara menentukan keuntungan pada suatu investasi agar bisa dianggap layak. Salah satu caranya menggunakan Capital Asset Pricing Model (CAPM). CAPM merupakan suatu penggambaran hubungan antara hasil (return) dan risiko dalam suatu model. CAPM bertujuan untuk meramalkan tingkat pengembalian (expected return) serta hubungannya dengan risiko.
Penelitian terkait CAPM dilakukan oleh, Yulianti et al. (2016) dalam penelitiannya, yaitu penerapan metode capital asset pricing model (CAPM) untuk menentukan penggelompokkan saham saham efisien dimana 7 emiten perusahaan asuransi terdapat 6 emiten perusahaan asuransi yang efisien dan 1 emiten perusahaan asuransi yang tidak efisien. Penelitian lain juga dilakukan oleh Wijaya et al. (2014) tentang implentasi CAPM dalam penentuan saham efisien, hasil penelitiannya adalah tiga saham yang terpilih dari sektor perbankan, ternyata 2 saham perusahaan perbankan termasuk efisien dan 1 saham perbankan tidak efisien.
Asuransi merupakan bagian ekonomi yang berkembang pesat di Indonesia dimana ditandai dengan banyaknya perusahaan asuransi di Indonesia. Selain itu, perusahaan asuransi berperan pada pertumbuhan ekonomi suatu Negara. Berdasarkan penjelasan tersebut, maka dilakukan penelitian yang berjudul “Menentukan Saham yang Efisien dengan Menggunakan Metode Capital Asset Pricing Model”.
Capital Asset Pricing Model
Menurut Bodie, et al. (2014:293)
menyatakan, bahwa CAPM adalah peramalan antara tingkat pengembalian dan risiko. Sedangkan Tandelilin (2010:187), menyatakan bahwa model CAPM dapat menunjukkan hubungan tingkat pengembalian yang diinginkan dan risiko pada keseimbangan pasar.
Teynor, Sharpe, dan Lintner dalam Husnan (2001) memformulasikan CAPM dan membuktikan bahwa capital market line (CML) adalah liner, adalah :
ri -f = (fm - rf) βi (1)
atau
ri = rf(rm-rm)βi (2)
dengan ri merupakan suatu tingkat keuntungan yang diharapkan dari suatu saham, rf
merupakan suatu dari tingkat keuntungan bebas risiko, rm adalah tingkat keuntungan indeks pasar, dan βi adalah risiko suatu saham, dan (rn — f f )βi adalah risk premium. Semakin besar risk premium saham, maka ekspektasi risk premium semakin menigkat. Dengan demikian semakin tinggi pula keuntungan yang diharapkan untuk saham tersebut.
Penurunan CAPM
Andaikan suatu Portofolio yang memiliki suatu dari n saham, yang dinotasikan ρ memiliki tingkat pengembalian yang diharapkan (expected return) dan standar deviasi adalah sebagai berikut :
E(rP) = wIeITi+ + (1 - wi) E(Tm)T = 1,,n
(3)
dan standart deviasi :
σp = [wi2σi2 + (1 - wi)2σ^ (4)
1
+ 2wi(1 - wi+σimm,
untuk, i = 1,, n. Saat W i berubah, E(rp) dan σp akan berubah sebagai berikut :
dE(Γp)∕dwi = E(T1) - E(rm) (5)
dan
dσp/dwi = wi E(ri) + (1 (6)
- wi+ Emm+
Sekarang perubahan E( ) relatif terhadap perubahan dapat dihitung dengan
menggunakan persamaan (5) dan (6) sebagai berikut :
dE (rp)
d Op
= [E(ri)-E(rm)]σp (7)
-
- (1 - ) + (1 - 2 )
Persamaan (7) dapat diartikan sebagai kemiringan slope kurva im. Dalam ekuilibrium, tidak ada permintaan berlebih untuk aset i. Jadi, ketika Wi = 0 dalam persamaan (7) (bahwa σp=
), Kemiringan kurva adalah sebagai berikut :
Selanjutnya, kemiringan slope kurva im ketika = 0 harus sama dengan kemiringan CML, karena CML bersinggungan dengan EF tanpa batas efisien pada m dan EF tanpa batas efisien bersinggungan dengan im pada m. kemiringan CML dapat dilihat sama dengan [E(rm) - Tf]/σm. Kemiringan CML disamakan dengan kemiringan slope kurva im pada adalah sebagai berikut :
E(rm+ -rf _ [E(t) - E (rm)]σp(9)
dan, setelah penyederhanaan
Mengukur beta (β)
Risiko sistematis atau risiko beta adalah risiko yang tetap ada meskipun dilakukan diversifikasi dimana banyak dihadapi oleh setiap perusahaan. Faktor-faktor yang berpengaruh terhadap risiko sistematis
cenderung itu yang berasal dari faktor makro ekonomi. Faktor makro ekonomi meliputi inflasi, siklus bisnis, dan berita tentang kondisi ekonomi.
Adapun cara untuk mengukur beta saham, adalah :
COV (HGn) (11)
=
var ( rm )
atau
COV (HGn) (12)
l var ( rm )
dengan σi adalah standar deviasi tingkat keuntungan saham i, ^m , merupakan suatu volatilitas tingkat keuntungan portofolio pasar, Pim merupakan korelasi antara tingkat keuntungan saham dengan tingkat keuntungan portofolio pasar.
-
2. METODE PENELITIAN
Data yang digunakan dalam penelitian ini adalah data sekunder yaitu harga saham penutupan (closing price) per bulan dari bulan Februari 2016 sampai bulan Juli 2018. Data penelitian ini diperoleh dari perusahaan dalam sektor asuransi yang terdaftar di BEI tahun 2018 yang berjumlah 12 data saham perusahaan yang unggul dan yang memenuhi kriteria menjadi sampel sebagai berikut : Asuransi Bina Dana Arta Tbk (ABDA.JK), Asuransi Harta Aman Pratama Tbk (AHAP.JK), Asuransi Multi Artha Guna Tbk (AMAG.JK), Asuransi Bintang Tbk (ASBI.JK), Asuransi Dayin Mitra Tbk (ASDM.JK), Asuransi Jasa Tania Tbk (ASJT.JK), Asuransi Kresna Mitra Tbk (ASMI.JK), Asuransi Ramayana Tbk (ASRM.JK), Lippo General Insurance Tbk (LPGI.JK), Maskapai Reasuransi Indonesia Tbk (MREI.JK), Paninvest Tbk (PNIN.JK), Victoria Insurance Tbk (VINS.JK). Data tersebut diperoleh dari www.finance.yahoo.com, www.idx.co.id, www.edusaham.com, dan www.investing.com. Adapun langkah-langkah dalam penelitian ini adalah :
-
1. Mengumpulkan data saham yang masuk dalam subsektor asuransi di BEI periode Februari 2016 – Juli 2018, yaitu data
closing price pada akhir bulan.
-
2. Menghitung tingkat pengembalian saham individu ( ri ) dengan :
=
-
3. Menghitung tingkat pengembalian pasar ( ^m ) yaitu :
(IHSGt - IHSGt~1)
=1,2,…,12
-
4. Menghitung risiko beta masing-masing individu ( βi )
Pt =
-
5. Menghitung Tingkat Pengembalian yang diharapkan / Expected Return [E( ri)]
menurut CAPM yaitu :
E(∏)=rf + βi [E( Gn)-rf ] (16)
-
6. Membuat Plot Security Market Line (SML)
-
7. Menentukan saham yang efisien berdasarkan nilai ri sebenarnya dan Expected Return [E( ri)] CAPM
-
3. HASIL DAN PEMBAHASAN
-
3.1 Nilai Tingkat Pengembalian Saham
-
Individu
Perhitungan nilai tingkat pengembalian saham individu menggunakan Excel. Sebagai contoh adalah perhitungan nilai tingkat pengembalian pada saham ABDA.JK dengan nilai saham sebelumnya Rp 7.500 dan nilai saham sekarang Rp 7.200 adalah :
(7200 - 7500)
ri = 7500
= -0.04.
Nilai r1 = -0,04 berarti terjadi penurunan nilai saham sebesar 4% dibandingkan nilai sebelumnya. Plot return saham disajikan pada Gambar 1. sampai Gambar 3.
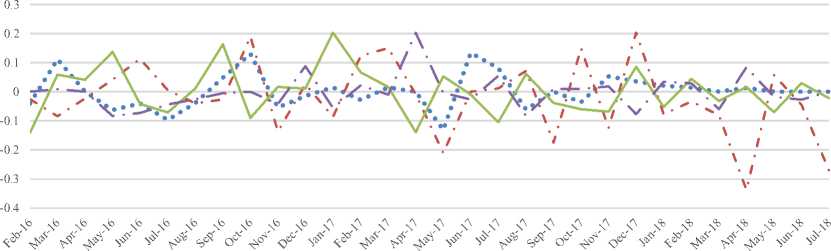
ABDA.JK
AHAP.JK
AMAG.JK
ASDM.JK
Gambar 1. Plot Return Saham ABDA.JK, AHAP.JK, AMAG.JK,ASDM.JK
Berdasarkan dari Gambar 1. seluruh return saham mengalami fluktuasi naik turun
dengan nilai terendah return saham AHAP.JK
periode April
2018.
0.8
√x √> ∖⅛ √? √a sV> χta s⅛o xta χt> χ⅛ ^ ^ x^ ^ sΛ ^ <λ ^ ^ <λ ^b ^b ^b ^b ςb ^b ςb
^ ^ ^ ^ √ ≠' ^ c^ θδ' √5^ ∕ ^ ^ 4^ ^ ^ ≠ ^ ^ c^ ^ ^' ^ ^ ^z ^' ^ ^ ^ ^
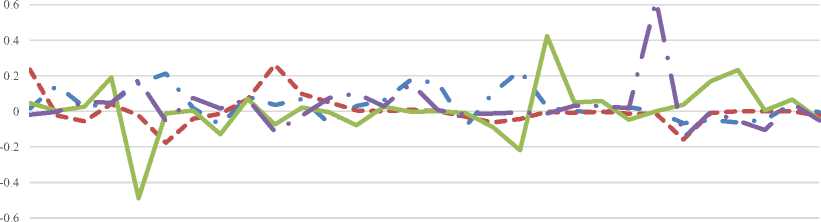
ASMI.JK LPGI.JK ■■■■■■■■I MREI.JK ^^^^B ∙ PNIN.JK
Gambar 2. Plot Return Saham ASMI.JK, LPGI.JK, MREI.JK, PNIN.JK
Berdasarkan dari Gambar 2. saham tersebut hanya mengalami fluktuasi yang signifikan pada periode tertentu. Misalkan return saham MREI.JK yang berfluktuasi tinggi pada
periode Juni 2016 dan September 2017 serta return saham PNIN.JK yang berfluktuasi tinggi pada periode Januari 2018.
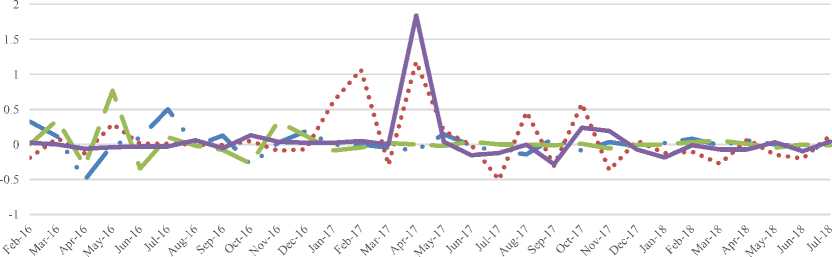
«■■MB B ASBI.JK ASJT.JK ^^^M ^B ASRM.JK ■■■■■■■■B VINS.JK
Gambar 3. Plot Return Saham ASBI.JK, ASJT.JK, ASRM.JK, VINS.JK
Berdasarkan dari Gambar 3. return saham ASBI.JK dan ASRM.JK mengalami fluktuasi yang signifikan pada tahun 2016 kemudian cenderung stabil hingga akhir periode. Sedangkan, saham ASJT.JK dan VINS.JK mengalami fluktuasi signifikan pada tahun 2017 sedangkan cenderung stabil.
-
3.2 Nilai Tingkat Pengembalian Pasar
-
( rm )
Indeks pasar yang digunakan penelitian ini adalah Indeks Harga Saham Gabungan (IHSG) karena mewakili aktivitas saham yang terdaftar di BEI. Sebagai ilustrasi, akan dihitung nilai tingkat pengembalian pasar saat harga IHSG sebelumnya Rp 4615,16 dan harga IHSG sekarang Rp 4770,96. Diperoleh hasil untuk nilai tingkat pengembalian pasar adalah sebagai berikut:
(4770.96 - 4615.16)
r1 = ----------------------
-
1 = 4615.16
= 0.03375831
Nilai rι = 0,03375831 berarti terjadi peningkatan harga pasar dari harga sebelumnya sebesar 3,375831%.
Selengkapnya lihat pada Tabel 1.
Tabel 1. Perhitungan Tingkat Pengembalian Pasar
|
Date |
IHSG |
rm |
|
Jan-16 |
4,615.16 | |
|
Feb-16 |
4,770.96 |
0.03375831 |
|
Mar-16 |
4,845.37 |
0.015596442 |
|
Apr-16 |
4,838.58 |
-0.001401338 |
|
May-16 |
4,796.87 |
-0.008620298 |
|
Jun-16 |
5,016.65 |
0.045817377 |
|
Jul-16 |
5,215.99 |
0.03973568 |
|
Aug-16 |
5,386.08 |
0.032609342 |
|
Sep-16 |
5,364.80 |
-0.003950925 |
|
Oct-16 |
5,422.54 |
0.01076275 |
|
Nov-16 |
5,148.91 |
-0.050461592 |
|
Dec-16 |
5,296.71 |
0.028705105 |
|
Jan-17 |
5,294.10 |
-0.000492759 |
|
Feb-17 |
5,386.69 |
0.017489281 |
|
Mar-17 |
5,568.11 |
0.03367931 |
|
Apr-17 |
5,685.30 |
0.021046639 |
|
May-17 |
5,738.15 |
0.009295903 |
|
Jun-17 |
5,829.71 |
0.015956362 |
|
Jul-17 |
5,840.94 |
0.001926339 |
|
Aug-17 |
5,864.06 |
0.003958267 |
|
Sep-17 |
5,900.85 |
0.00627381 |
|
Oct-17 |
6,005.78 |
0.017782184 |
|
Nov-17 |
5,952.14 |
-0.008931396 |
|
Dec-17 |
6,355.65 |
0.067792424 |
|
Date |
IHSG |
rm |
|
Jan-18 |
6,605.63 |
0.039331933 |
|
Feb-18 |
6,597.22 |
-0.001273156 |
|
Mar-18 |
6,188.99 |
-0.061879095 |
|
Apr-18 |
5,994.60 |
-0.031409002 |
|
May-18 |
5,983.59 |
-0.001836653 |
|
Jun-18 |
5,799.24 |
-0.030809263 |
|
Jul-18 |
5,936.44 |
0.023658272 |
|
Jumlah |
0.264110252 | |
|
rm |
0.008803675 | |
Beta (β) adalah suatu ukuran risiko pada suatu saham. Beta adalah hasil bagi antara kovarian saham dan varians pasar yang menunjukkan hubungan antara return saham dan return market. Beta disajikan Tabel 2.
Tabel 2. Perhitungan Hasil Risiko Beta
Masing -masing Individu (β i)
|
No |
Kode Saham |
Beta |
Kovarians |
Varians Pasar |
|
1 |
ABDA |
0.0066774 |
0.000005014 |
0.0007510 |
|
2 |
AHAP |
0.0344 |
0.00155 |
0.0007510 |
|
3 |
AMAG |
-0.442 |
-0.00033 |
0.0007510 |
|
4 |
ASBI |
1.206 |
0.00091 |
0.0007510 |
|
5 |
ASDM |
0.088 |
0.000066 |
0.0007510 |
|
6 |
ASJT |
2.213 |
0.001661883 |
0.0007510 |
|
7 |
ASMI |
0.997 |
0.000748362 |
0.0007510 |
|
8 |
ASRM |
-1.629 |
-0.001223467 |
0.0007510 |
|
9 |
LPGI |
-0.635 |
-0.000476475 |
0.0007510 |
|
10 |
MREI |
-1.853 |
-0.00139139 |
0.0007510 |
|
11 |
PNIN |
1.605 |
0.00120521 |
0.0007510 |
|
12 |
VINS |
1.1 |
0.00082582 |
0.0007510 |
Berdasarkan dari Tabel 2, diperoleh nilai beta saham yang negatif pada saham AMAG.JK, ASRM.JK, LPGI.JK, dan MREI.JK yang berarti apabila terjadi kenaikan pada pasar maka saham tersebut nilainya akan turun. Sebaliknya, nilai beta saham yang positif pada saham ABDA.JK, AHAP.JK, ASBI.JK, ASDM.JK, ASJT.JK, ASMI.JK, PNIN.JK, dan VINS.JK berarti apabila harga pasar naik maka saham tersebut ikut naik.
-
3.4 Tingkat Pengembalian yang
diharapkan / Expected Return [E(ri)] menurut CAPM
Metode CAPM itu digunakan untuk menghitung suatu tingkat pengembalian yang diharapkan dengan cara input berupa variabel tingkat pengembalian saham masing-masing individu, tingkat pengembalian pasar, tingkat pengembalian bebas risiko, dan risiko beta pada masing-masing saham.
Tabel 3. Perhitungan Tingkat Pengembalian Yang Diharapkan
|
Kode |
ri |
E(ri) |
|
ABDA |
0.003381 |
0.0042884 |
|
AHAP |
-0.02149 |
0.0136137 |
|
AMAG |
0.002389 |
0.0022487 |
|
ASBI |
0.012208 |
0.0097405 |
|
ASDM |
-0.00285 |
0.0046580 |
|
ASJT |
0.06575 |
0.0143183 |
|
ASMI |
0.039515 |
0.0087904 |
|
ASRM |
0.017498 |
-0.0031474 |
|
LPGI |
0.002108 |
0.0013736 |
|
MREI |
0.006254 |
-0.0041657 |
|
PNIN |
0.030687 |
0.0115543 |
|
VINS |
0.048288 |
0.0092586 |
Berdasarkan dari Tabel 3., diperoleh saham ASRM.JK dan MREI.JK memiliki Expected Return yang negatif ini berarti saham tersebut cenderung memiliki nilai harga saham turun. Selain, itu nilai Expected Return saham lainnya positif yang berarti memiliki nilai saham yang cenderung meningkat.
Nilai E (r) yang telah diperoleh pada Tabel 3. dan nilai beta pada Tabel 2. digunakan untuk menggambar grafik Security Market Line (SML). Grafik yang diperoleh dapat dilihat pada Gambar 4.
0.02
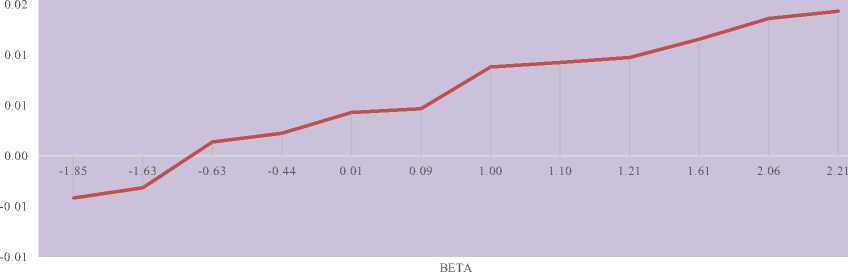
Gambar 4. Grafik Security Market Line ( SML)
Berdasarkan Gambar 4. diperoleh, bahwa kenaikkan nilai beta akan diikuti oleh kenaikan nilai Expected Return. Ini berarti nilai return dan nilai expected return memiliki korelasi yang positif (Hubungan positif).
-
3.6 Menentukan Saham yang Efisien Berdasarkan Nilai Return sebenarnya dan Expected Return
Nilai return terakhir pada setiap saham dan nilai expected return yang diperoleh dari Tabel 3. dapat digambarkan grafik untuk saham-saham yang efisien. Grafik disajikan pada Gambar 5.
Perbandingan dan Posisi Antara Tingkat Pengembalian Saham Individu dan Tingkat yang Diharapkan
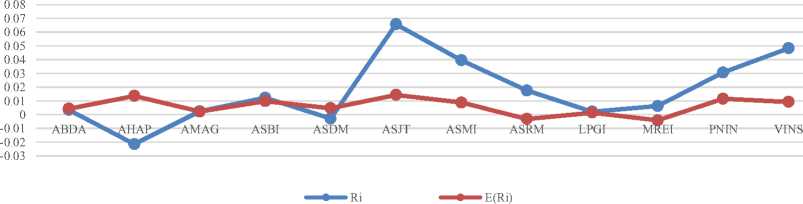
Gambar 5. Perbandingan dan Posisi Antara Tingkat Pengembalian Saham Individu dan Tingkat Pengembalian yang Diharapkan
Berdasarkan dari Gambar 5. bahwa nilai return yang ada di atas garis expected return adalah saham AMAG.JK, ASBI.JK, ASJT.JK, ASMI.JK, ASRM.JK, LPGI.JK, MREI.JK, PNIN.JK, dan VINS.JK. Ini berarti saham-saham tersebut dikatakan efisien karena
memiliki nilai return lebih tinggi daripada expected return. Gambar 5. juga dapat disajikan pada Tabel 4.
Tabel 4. Pengelompokkan Saham Efisien, Tidak Efisien dan Keputusan Investasi Saham
|
Kode Saham |
n |
E(ri) |
r - E(ri) |
Evaluasi Saham |
|
ABDA |
0.003381 |
0.004310 |
-0.000929 |
tidak efisien |
|
AHAP |
-0.02149 |
0.004414 |
-0.025902 |
tidak efisien |
|
AMAG |
0.002389 |
0.002249 |
0.000140 |
efisien |
|
ASBI |
0.012208 |
0.009740 |
0.002467 |
efisien |
|
ASDM |
-0.00285 |
0.004658 |
-0.007512 |
tidak efisien |
|
ASJT |
0.06575 |
0.014318 |
0.051432 |
efisien |
|
ASMI |
0.039515 |
0.008790 |
0.030724 |
efisien |
|
ASRM |
0.017498 |
-0.003147 |
0.020645 |
efisien |
|
LPGI |
0.002108 |
0.001374 |
0.000734 |
efisien |
|
MREI |
0.006254 |
-0.004166 |
0.010420 |
efisien |
|
PNIN |
0.030687 |
0.011554 |
0.019132 |
efisien |
|
VINS |
0.048288 |
0.009259 |
0.039029 |
efisien |
Berdasarkan Tabel 4. diperoleh bahwa ri — E (ri) selisih positif menandakan nilai return saham lebih tinggi daripada expected return ini berarti saham-saham dikatakan saham yang efisien. Sebaliknya saham-saham dengan nilai selisih return dan tingkat yang diharapkan bernilai negatif maka dikatakan saham yang tidak efisien.
Berdasarkan hasil dan pembahasan yang Pembahasan mengenai CAPM menunjukkan bahwa CAPM mampu menunjukkan saham yang efisen dengan melihat apakah selisih nilai return sebenarnya dengan nilai expected return CAPM bernilai positif/negatif. Adapun langkah-langkah yang dilakukan pada CAPM adalah menghitung tingkat pengembalian individu saham individu (rj), selanjutnya menghitung tingkat pengembalian pasar (rn), kemudian menghitung risiko beta masing-masing individu (β i), lalu menghitung tingkat pengembalian yang diharapkan / expected return [E (ri)] menurut CAPM, dilanjutkan dengan membuat plot Security Market Line (SML), dan akhirnya menghitung saham yang efisien berdasarkan nilai ri sebenarnya dan expected return CAPM. Diantara saham-saham yang digunakan dalam penelitian ini, saham-saham yang efisien adalah AMAG.JK, ASBI.JK, ASJT.JK, ASMI.JK, ASRM.JK, PNIN.JK, VINS.JK, LPGI.JK, MREI.JK. Sedangkan, sisanya saham yang tidak efisien adalah ABDA.JK, AHAP.JK, ASDM.JK.
Berdasarkan penelitian yang telah dilakukan, maka saran yang dapat diberikan oleh peneliti yaitu :
-
1. Untuk pengembangan penelitian
selanjutnya, diharapkan membandingkan estimasi CAPM dengan APT untuk
melihat apakah saham yang efisien yang dihasilkan sama.
-
2. Diharapkan adanya penelitian lebih lanjut mengenai suatu subsektor, sampel dan periode penelitian yang berbeda, sehingga mengenai perkembangan dalam dunia investasi di pasar modal dapat diketahui lebih lanjut.
DAFTAR PUSTAKA
Amelia,Viky., Dharmawan, K., & Widana, N.
I. (2017). Membandingkan Risiko Sistematis Menggunakan CAPM-GARCH Dan CAPM-EGARCH. E-Jurnal
Matematika, Volume 6 No 4, hlm 241 -247.
Bodie, Alex, K. & Alan, M., 2014.
Manajemen Portofolio dan Investasi. Jakarta: Salemba Empat.
Francis, J. C. & Kim, D., 2013. Modern Portofolio Theory + WS, New York: s.n.
Husnan & Suad, 2001. Dasar-dasar Teori Portofolio dan Analisis Sekuritas Edisi ketiga. Yogyakarta: UPP AMP YKPN.
Sharpe & William, F., 1997. Theory & Capital Market. New York: McGraw-Hill.
Tandelilin & Eduardus, 2010. Portofolio dan Investasi: Teori dan Aplikasi. Edisi
Pertama. Yogyakarta: Kanisius.
Wijaya & John, H., 2014. Implementasi
Capital Asset Pricing Model (CAPM) Dalam Penentuan saham Efisien : Studi pada BCA, BRI, dan BNI Periode 20122013. Study & Management Research, 11(3).
Yulianti, R., Topowijono & Azizah, D. F., 2016. Penerapan Metode Asset Pricing Model Untuk Menentukan Kelompok Saham-saham Efisien. Jurnal Administarsi Bisnis, 38(2), pp. 122-130.
Zubir & Zalmi, 2010. Manajemen Portofolio: Penerapannya dalam Investasi Saham. Jakarta: Salemba Empat.
30
Discussion and feedback