E-Jurnal Matematika Vol. 9(1), Januari 2020, pp.31-36

DOI: https://doi.org/10.24843/MTK.2020.v09.i01.p275

ISSN: 2303-1751

FAKTOR-FAKTOR YANG BERPENGARUH SIGNIFIKAN TERHADAP INDEKS PEMBANGUNAN MANUSIA

DI PROVINSI PAPUA

Ina Azizah Kadri1§, Made Susilawati2, Kartika Sari3

§Corresponding Author

ABSTRACT

Geographically weighted regression (GWR) analysis is one of an analysis to resolve the problem with data contains effect of spatial heterogenity. One of the problems which considers spatial heterogeneity is human development index (HDI). HDI is an indicator that used to measure success in building quality of human life. One of the provinces with the lowest HDI in Indonesia is Papua. The purpose of this research is to know the contribution of each HDI factors in Papua using GWR method. The weighting function used is adaptive gaussian kernel. The results of this research showed HDI’s dominant factors in Papua, expected years of schooling and mean years of schooling.

Keywords: geographically weighted regression (GWR), spatial heterogeneity, HDI.

  • 1.    PENDAHULUAN

Indeks pembangunan manusia (IPM) adalah indikator yang digunakan untuk mengukur kualitas hidup manusia. Pencapaian angka IPM memberikan indikasi peningkatan atau penurunan kinerja pembangunan manusia. Salah satu provinsi di Indonesia dengan capaian IPM terendah adalah Provinsi Papua. Berdasarkan data BPS 2017, IPM di Provinsi Papua pada tahun 2016 hanya mencapai 58,08 (kurang dari 60). Angka ini meningkat sebesar 0,8 dari tahun sebelumnya. Namun meskipun mengalami peningkatan, IPM di Provinsi Papua masih dalam kategori rendah.

Faktor – faktor yang memengaruhi capaian IPM di setiap wilayah berbeda – beda. Hal ini disebabkan karena adanya perbedaan karakteristik suatu wilayah dengan wilayah lain. Perbedaan karakteristik antarwilayah menimbulkan efek spasial atau disebut heterogenitas spasial. Salah satu metode untuk mengatasi masalah spasial tersebut adalah metode geographically weighted regression (GWR) (Fotheringham, et al., 2002).

Secara umum model GWR dapat ditulis sebagai

∑

βk (^i , Vi ) xik + Zi .

k=l

dengan i menyatakan lokasi amatan ( = 1,2,3,⋯,n), n menyatakan banyaknya pengamatan, Vi menyatakan variabel terikat pada pengamatan ke- i, xik merupakan variabel bebas ke-k pada pengamatan ke- i, βo dan βk merupakan parameter regresi ke-k untuk k=1,2,…,P, βo (Ui, vi ) menyatakan konstanta regresi pada lokasi ke-i, βk (Ui, vi ) xik menyatakan koefisien regresi pada lokasi ke-i dengan variabel bebas ke-k, Ui sebagai titik koordinat spasial (lintang) untuk pengamatan ke-i vi sebagai titik koordinat spasial (bujur) untuk pengamatan ke-i dan εi merupakan error yang berdistribusi normal N (0, σ2 ) pada pengamatan ke-i.

Hal yang paling mendasar pada GWR adalah kedekatan antarwilayah yang ditunjukkan melalui matriks pembobot. Fungsi pembobot yang digunakan dalam penelitian ini adalah adaptive kernel gaussian. Fungsi ini memiliki bandwidth yang berbeda untuk setiap lokasi pengamatan (Fotheringham, et al., 2002).

Metode GWR merupakan metode yang sering digunakan untuk masalah spasial. Susanti dkk. (2016) juga melakukan penelitian

tentang pemodelan tingkat kesejahteraan penduduk Provinsi Kalimantan Selatan menggunakan geographically weighted regression. Penelitian tersebut menghasilkan bahwa faktor-faktor yang berpengaruh secara signifikan adalah tingkat melek huruf penduduk, tingkat partisipasi sekolah, dan presentase balita kekurangan gizi. Penelitian sebelumnya terkait IPM dilakukan oleh Widyastuti dkk. (2018) yang meneliti indeks pembangunan manusia di Kalimantan menggunakan geographically weighted logistic regression. Penelitian tersebut menghasilkan bahwa faktor-faktor yang berpengaruh secara signifikan untuk IPM di Kalimantan adalah persentase penduduk miskin, persentase pengangguran terbuka, persentase penduduk yang lulus perguruan tinggi dan banyaknya jumlah tenaga kesehatan (dokter, bidan, perawat dan apoteker).

  • 2.    METODE PENELITIAN

Data yang digunakan pada penelitian ini adalah data sekunder mengenai Indeks Pembangunan Manusia (IPM) untuk setiap Kabupaten/Kota di Papua yang bersumber dari Badan Pusat Statistik (BPS) tahun 2017 Provinsi Papua.

Variabel yang digunakan meliputi variabel terikat (Y) yaitu indeks pembangunan manusia di Provinsi Papua dan variabel bebas (X). Variabel bebas (X) antara lain angka harapan hidup ( ^l ), harapan lama sekolah ( ^2), rata – rata lama sekolah ( ^3), dan pengeluaran per kapita ( *4 )

Langkah-langkah yang dilakukan adalah

  • 1.    Mengumpulkan data mengenai indeks pembangunan manusia di masing-masing Kabupaten/Kota yang di kategorikan sebagai variabel terikat (Y) dan keempat variabel bebasnya serta data geografis letak titik koordinat masing-masing Kabupaten/ Kota di Papua.

  • 2.    Memodelkan indeks pembangunan manusia menggunakan regresi linear berganda.

Yi =   + βl×il + β2xt2+⋯+

βpxip + Zi                           (1)

  • 3.    Memeriksa  kenormalan dari residual

menggunakan uji Anderson Darling dengan hipotesis:

Hq ∶ Residual berdistribusi normal

Hi ∶ Residual tidak berdistribusi normal Statistik uji yang digunakan adalah

5.


A2 =-n- ⅛ ∑ !U (2 i-1) { lnF( Yi)+ ln[1 - F(Yn+i+i)} (2)

dengan F( Yi) menyatakan fungsi sebaran kumulatif dari normal baku dan Yi menyatakan data yang diurutkan (Algifari, 2000).

Keputusan:  Terima Hq pada taraf

signifikasi a jika A2 < ADiaijei atau Pvalue ≥a . Jika tidak normal, maka dilakukan transformasi data.

  • 4.    Memeriksa multikolinearitas dari variabel-

variabel bebas dengan melihat nilai VIF pada setiap variabel bebas. Jika nilai VIF > 5 maka terdapat multikolinearitas. Salah satu metode yang dapat digunakan untuk mengatasi multikolinearitas adalah metode stepwise. Statistik uji yang digunakan adalah

VIFj =

J I-Rj

(3)


dengan Rf


merupakan koefisien


determinasi antara      dengan variabel

prediktor lainnya pada model regresi dengan j=1,2,…,P . Jika terdapat multikolinearitas, maka pada penelitian ini digunakan metode stepwise (Draper & Smith, 1992).

Memeriksa heteroskedastisitas pada residual menggunakan uji Breush Pagan (Anselin, 1988) dengan hipotesis uji: H0 :   =   =⋯=   = (Tidak

terjadi heteroskedastisitas pada data).

∏1 : Minimal ada satu σi2 ≠ σ2 (Terjadi heteroskedastisitas pada data).

Statistik uji yang digunakan adalah

BP =     (XrX) ~1Xτ f          (4)

dengan f menyatakan vektor berukuran (n×1)  yang berisi f=[fi , f2,…,fn ]

dengan

p∙2 fi ̂2 -1 ̂2= ∑ eI2

̂)2


e2 =∑F=i( Yt -


Notasi BP menyatakan nilai Breusch Pagan, ̂ 2 menyatakan varian sisaan, dan ei2 menyatakan nilai kuadrat sisaan.

Keputusan: Tolak Hq apabila nilai BP ≥ Xk2 dengan taraf signifikan a atau Pvalue <a(0,05).

Jika tidak terjadi heteroskedastisitas maka berhenti di langkah ini.

6.


a.


b.


Membentuk model geographically weighted regression (GWR) berdasarkan persamaan berikut

Vi = (ui, Vi)+∑Li βk (Ui, Vi) Xik + ^i

(5)

Menentukan Ui dan vi berdasarkan garis lintang selatan dan garis bujur timur untuk Kabupaten/Kota i di Papua.

Menghitung jarak Euclid antarkabupaten dan kota berdasarkan letak geografis menggunakan rumus:


g. Menguji signifikasi parameter model


GWR dengan uji t dengan hipotesis

H0 :  (ui , vi)=0

Hy :Minimal ada satu βk (Ui, vi)≠0 Statistik uji yang digunakan adalah


^hitung dengan


̂

Pk (^i , Yi ) SE ̂ *(ui,vi)


(10)


c.


d.


e.


Ui - Uj) +(vi -


2 vJ )


(6)


SE ̂k( ,Vi)=√var ̂k( ,Vi)=√CCt ̂2 C=(XtW(ui, vi )X) 1XtW(ui, vi)


^2

̂


∑Γ=ι(Y1- ̂i)2


Menentukan nilai bandwidth nilai CV menggunakan rumus

CV=∑F=ι(yi - ̂ ≠i (b))2

Bandwidth optimum yang


berdasarkan


(7) digunakan


adalah bandwidth dengan nilai CV terkecil. Menentukan matriks pembobot yang entri-entrinya menggunakan fungsi adaptive gaussian kernel dengan persamaan


wij' =exp


-


δι


β ii (, ) menyatakan koefisien regresi pada koordinat letak geografis (lintang, bujur) ke-i dan SEβ ic (, ) menyatakan


2'


( )


Menduga parameter model Pendugaan parameter model dilakukan dengan menggunakan weighted least square (WLS).


(8)


GWR.

GWR metode


standar error penduga parameter βk , CCt ̂2 menyatakan matriks varians dan kovarians pada pengamatan ke-i , dan ̂ 2 menyatakan jumlah kuadrat residual dari regresi GWR global.

Nilai ^tabel dapat dicari dengan distribusi

t menggunakan derajat bebas df =

θ2 pada taraf signifikan a.


f. Menguji kesesuaian model GWR dengan uji F (Fotheringham, et al., 2002) dengan hipotesis

¾:  (^i , Vi)=βk

Hy : Minimal ada satu βk (Ui, Vi)≠βk Statistik uji yang digunakan adalah

RSS(H0)-RSS(⅛1)


Keputusan: Tolak H0 jika ^hitung ≥ ⅛abel dengan taraf signifikan a atau Pvalue <a. Hal ini berarti ada pengaruh signifikan antara variabel bebas dengan variabel terikat.


3. HASIL DAN PEMBAHASAN


F,.-

rhιtung =       ( Hi )


(9)


δl

RSS(Hq) menyatakan jumlah kuadrat sisaan model regresi linear klasik dan RSS(Hi) menyatakan jumlah kuadrat sisaan model GWR (Leung, et al., 2000). Ftabel dapat dicari dengan distribusi F τ 2 menggunakan derajat bebas      =

τ2

dan df2 = pada taraf signifikan a, Vi =  [(I-H)-(I-L)T(I-L)] i,

dan ^i =   [(I-L)T(I-L)] i dengan

i=1,2

Keputusan: Hipotesis ∏o ditolak jika Fhitung ≥ Ftabel . Hal ini berarti ada perbedaan signifikan antara model regresi linear dengan GWR.


Gambaran umum mengenai indeks pembangunan manusia di Provinsi Papua disajikan pada Tabel 1.


Tabel 1. Statistika Deskriptif

Var

Min

Max

Mean

StDev

Y

27,87

79,23

55,76

11,70

X1    ∖

54,60

71,93

64,47

3,95

X2    ∖

2,64

14,98

9,86

2,99

X3    ∖

0,71

11,15

5,75

2,99

X4    ∖

3,97

14,78

6,83

2,57


Tabel 1 memperlihatkan indeks pembangunan manusia (Y) terendah sebesar 27,87. Pada kolom minimum, semua data tersebut berasal dari Kabupaten Nduga. Untuk angka harapan hidup (Xy) sebesar 54,60 yang artinya tiap bayi yang baru lahir di Kabupaten Nduga memiliki perkiraan rata-rata umur yang diharapkan untuk hidup sebesar 54,60 atau


sekitar 55 tahun. Harapan lama sekolah (X2) sebesar 2,64 bermakna lamanya sekolah yang diharapkan akan dirasakan oleh anak-anak usia 7 tahun di Kabupaten Nduga dimasa mendatang sebesar 2,64 tahun atau hanya lulus kelas 2 SD. Selanjutnya rata-rata lama sekolah (X3 ) sebesar 0,71 yang berarti penduduk di Kabupaten Nduga yang berusia 25 tahun ke atas secara rata-rata menempuh pendidikan formal selama 0,71 tahun atau tidak lulus kelas 1 SD. Sedangkan untuk pengeluaran per kapita (X4) di Kabupaten Nduga sebesar 3,97 yang berarti secara rata-rata pengeluaran penduduk Kabupaten Nduga selama setahun adalah 3,97 juta. Selanjutnya pada penelitian ini, taraf signifikan (α) yang digunakan sebesar (0.05).

Setelah melakukan analisis deskriptif, akan dibentuk model indeks pembangunan manusia di Provinsi Papua menggunakan analisis regresi berganda. Analisis regresi berganda bertujuan

untuk mengetahui hubungan variabel bebas dengan variabel terikat. Diperoleh persamaan regresi linear berganda menggunakan software Minitab 17.

̂i = -4,127 + 0,4738 *1 + 1,473 X2 + 1,463 X3 + 0,9372 *4                     (11)

Persamaan (1) memiliki nilai koefisien korelasi (R2) sebesar 99,33%. Hal ini berarti variabel bebas mampu menjelaskan indeks pembangunan manusia secara umum sebesar 99,21%. Sisanya sebesar 0,79% dijelaskan oleh variabel lain di luar model.

Regesi linear mensyaratkan asumsi-asumsi, diantaranya normalitas residual, tidak ada multikolinearitas antarpeubah bebas dan ragam bersifat homogen.

Uji kenormalan ini bertujuan untuk melihat apakah nilai residual berdistribusi normal atau tidak. Hasil uji kenormalan ditampilkan pada Gambar 1.

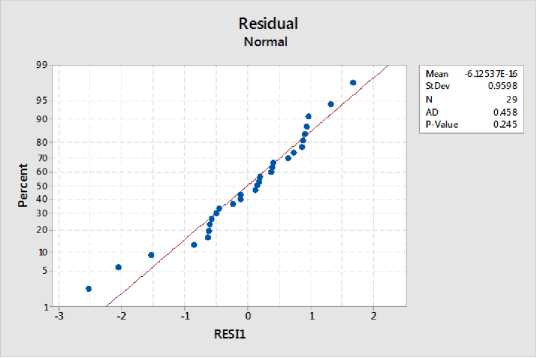
Gambar 1. Uji Kenormalan


Hasil uji Anderson Darling dapat dilihat pada Gambar 1. Tampak bahwa nilai = 0,245 ≥ a. Ini berarti residual yang dihasilkan pada model regresi linear berdistribusi normal.

Pemerikasaan multikoliniearitas dilakukan untuk mengetahui adanya korelasi antarvariabel bebas yang memengaruhi variabel terikat. Hasil uji multikolinearitas dapat dilihat pada Tabel 2.

Tabel 2. Hasil Uji Multikoliniearitas

(X i)

VIF

X1        ∖

1,421528

X2        ∖

4,929688

X3        ∖

7,611009

X4       ∖

3,474465

Hasil uji multikoliniearitas pada Tabel 2 adalah terdapat multikoliniearitas antarvariabel bebas. Hal ini ditunjukkan variabel bebas X3 bernilai VIF≥5. Jika ada gejala multikolinearitas maka diselesaikan menggunakan metode stepwise.

Metode stepwise merupakan gabungan dari metode backward elimination dan metode fordward selection. Kriteria dalam pemilihan variabel yang masuk ke model adalah variabel yang memiliki nilai korelasi tertinggi dan memiliki nilai signifikan yang kurang dari a.

Berdasarkan analisis menggunakan metode stepwise diperoleh model terbaik sebagai berikut:

̂i = -4,128 + 1,463 *3 + 0,474X1 + 1,1473X2 + 0,937X4 (12)

Persamaan tersebut merupakan model terbaik dengan variabel bebas yang berpengaruh    signifikan di beberapa

kabupaten/kota di Provinsi Papua. Dari model di atas terlihat bahwa semua variabel bebas masuk ke dalam model dan masih terjadi multikolinearitas. Hal ini dapat disimpulkan bahwa kasus multikolinearitas yang terjadi tidak dapat diselesaikan menggunakan metode stepwise. Perlu dilihat variabel X3 memiliki korelasi yang tinggi dengan ^2 yaitu sebesar 0.892. Hal ini menandakan kasus multikolinearitas pada IPM di Provinsi Papua tidak dapat diatasi karena korelasi antarvariabel bebas sangat erat. Untuk selanjutnya dapat digunakan metode analisis komponen utama (AKU), pada penelitian kali ini peneliti hanya menggunaka metode stepwise.

Uji heteroskedastisitas bertujuan untuk mengetahui ada tidaknya ketidaksamaan varian dari residual untuk semua pengamatan.

Hasil uji heteroskedastisitas diperoleh nilai Pvalue = 0,009189 lebih kecil dari taraf siginifikasi a. Hal ini dapat disimpulkan bahwa terdapat heteroskedastisitas pada data.

Pengaruh heteroskedastisitas menyebabkan model regresi linear perlu dilakukan pemodelan lebih lanjut. Salah satu metode yang dapat digunakan untuk mengatasi heteroskedastisitas yaitu dengan menggunakan metode weighted least regression (WLS).

Memodelkan GWR lokal, peneliti mengambil contoh pada Kabupaten Nduga. Matriks pembobot dalam penelitian ini menggunakan fungsi pembobot kernel adaptive gaussian yang memerlukan jarak Euclid (uij, vij,) dan nilai bandwidth tertentu (bi).

Pemilihan bandwidth optimum dilakukan dengan proses berulang-ulang sehingga memperoleh nilai CV terkecil. Perolehan bandwidth optimum di Kabupaten Nduga sebesar 143,7815 km.

Fungsi pembobot adaptive kernel gaussian untuk Kabupaten Nduga diperoleh dengan

persamaan

1 ( ^■tj ___∖2I

wii=exp- .     /

p      ∖143 .7815/ J

Model GWR yang terbentuk dari matriks pembobot Kabupaten Nduga adalah

̂ Kab .Nduga = -5,88314 +0,468189Xi

+1,688333X2 +1,396168X3 +1,054283X4

Dilakukan uji kesesuaian model GWR.

Pengujian ini bertujuan untuk mengetahui ada atau tidak perbedaan yang signifikan antara model regresi linear dengan GWR.

Statistik uji:

Fhitung = 2,726746

Sedangkan,

Ftabel(O,05;6.277479;17.72252)= 0,255868

Keputusan:

Hipotesis menolak Hq karena         =

2,726746 ≥ Ftabel = 0,255868. Hal ini berarti ada perbedaan signifikan antara model regresi linear dengan GWR. Model GWR lebih layak untuk menggambarkan indeks pembangunan manusia di Provinsi Papua 2017.

Setelah melakukan uji kesesuaian model, dilakukan uji signifikan parameter pada model GWR. Pengujian ini bertujuan untuk mengetahui pengaruh antara variabel bebas dengan variabel terikat pada setiap kabupaten.

Tabel 3. Hasil Uji t Kabupaten Nduga

Variabel

( ̂)

^hitung

Intersep

-5,88314

-1,75592

Xi

0,468189

8,44714

χ2

1,688333

11,81236

χ2

1,396168

6,87777

X4

0,001054

5.52519

Berdasarkan Tabel 3 nilai ^hitung ≥ ^tabel(0,05;25) =2,059539 yang berarti menolak Hq . Variabel bebas yang berpengaruh signifikan untuk indeks pembangunan manusia di Kabupaten Nduga dipengaruhi oleh angka harapan hidup ( ^l), harapan lama sekolah (%2 ), rata – rata lama sekolah ( ¾ ), dan pendapatan per kapita ( ¾).

Setelah diperoleh model GWR untuk masing-masing pengamatan, selanjutnya melakukan interpretasi model GWR. Sebagai contoh interpretasi pada Kabupaten Nduga

̂ Kab .Nduga = -5,88314 +0,468189Xi +1,688333X2 +1,396168X3 +1,054283X4

Model dapat diartikan jika presentase angka harapan hidup ( ^l ) bertambah satu tahun dengan menganggap variabel bebas yang lain konstan maka indeks pembangunan manusia akan meningkat sebesar 0,468189 persen. Interpretasi juga berlaku untuk untuk variabel bebas lainnya. Terjadi peningkatan maupun penurunan tergantung variabel bebas yang diperoleh.

4. SIMPULAN DAN SARAN

Faktor-faktor yang berpengaruh signifikan terhadap indeks pembangunan manusia untuk setiap kabupaten dan kota di Provinsi Papua adalah angka harapan hidup (X1 ), harapan lama sekolah (X2 ), rata-rata lama sekolah (X3 ), dan pengeluaran per kapita (X4). Konstribusi dari masing-masing faktor untuk setiap kabupaten dan kota di Provinsi Papua berbeda-beda. Faktor yang memberikan konstribusinya paling besar untuk semua wilayah adalah faktor pendidikan yang terdiri dari harapan lama sekolah (X2 ), rata-rata lama sekolah (X3 ). Sedangkan kontribusi yang paling kecil untuk semua wilayah adalah faktor ekonomi berupa pengeluaran per kapita.

Pada penelitian ini, efek multikolinearitas masih belum teratasi. Sehingga untuk peneliti selanjutnya yang akan mengambil kasus yang sama dan terjadi multikolinearitas sebaiknya menggunakan metode analisis komponen utama (AKU). Selain itu, penelitian berikutnya dapat melakukan kajian yang lebih lanjut mengenai variabel bebas yang digunakan serta menggunakan indeks pembangunan manusia yang lebih spesifik seperti tingkat kecamatan agar mendapatkan hasil yang akurat.

DAFTAR PUSTAKA

Algifari, 2000. Analisis Regresi (Teori, Kasus dan Solusi). 2nd penyunt. Yogyakarta: BPFE.

Anselin, L.,  1988. Spatial Econometrics:

Methods and Models. Netherland: Kluwer Academic Publisher.

BPS, 2017. Indeks Pembangunan Manusia 2014 Metode Baru. Jakarta: Badan Pusat Statistika.

BPS, 2018. Provinsi Papua Dalam Angka 2018. Jakarta: Badan Pusat Statistika.

Draper, N. R. & Smith, H., 1992. Applied

Regression Analysis. New York: John Wiley and Sons.

Fotheringham, A. S., Brunsdon, C. & Charlton, M.,   2002. Geographically Weighted

Regression : Analysis of Spatially Varying Relationship. England: John Wiley and Son.

Leung, Y., Mei, C. L. & Zhang, W. X., 2000.

Statistic Test for Spatial Non-Stationarity

Based on the Geographically Weighted Regression Model. Environment and Planning, A(32), pp. 9-32.

Susanti, D. S., Lestia, A. S. & Sukmawaty, Y., 2016. Pemodelan Tingkat Kesejahteraan Penduduk Propinsi Kalimantan Selatan dengan Pendekatan Geographically Weighted Regression. Jurnal Eksponensial. I(1), pp. 184-191.

Widyastuti, L., Yuniarti, D. & Hayati, M. N., 2018. Pemodelan Faktor-Faktor yang Berpengaruh      Terhadap      Indeks

Pembangunan Manusia (IPM) di Kalimantan dengan Geographically Weighted Logistic Regression (GWLR). Jurnal Eksponensial, IX(1), pp. 67-74.

36