E-Jurnal Matematika Vol. 9(1), Januari 2020, pp.14-22

DOI: https://doi.org/10.24843/MTK.2020.v09.i01.p273

ISSN: 2303-1751

PERBANDINGAN ANALISIS DISKRIMINAN DAN REGRESI LOGISTIK UNTUK MENGKLASIFIKASIKAN KELAYAKAN VISITASI PELAMAR BIDIKMISI

Nisa Hidayati1§, I Komang Gde Sukarsa2, Desak Putu Eka Nilakusmawati3

1Program Studi Matematika, Fakultas MIPA – UniversitasUdayana [Email: nisa.hidayati44@gmail.com] 2Program Studi Matematika, Fakultas MIPA – UniversitasUdayana [Email: sukarsakomang@yahoo.com] 3Program Studi Matematika, Fakultas MIPA – UniversitasUdayana [Email: nilakusumawati@unud.ac.id]

§Corresponding Author

ABSTRACT

The purpose of this study is to compare discriminant analysis and logistic regression to classify the feasibility of the Bidikmisi applicant's visitation based on the classification accuracy. The results showed that the assumptions of homogeneity covariance matricies between the groups are unequal, The significant independent variable is the combined amount of parental income (X1 ), parents income divided by the number of family dependents (X2 ), and electricity bills (X6), and then the results of the classification of validation data from the logistic regression analysis of 98,21% higher than the discriminant analysis of 94,64%.

Keywords: Discriminant Analysis, Logistic Regression, Bidikmisi Scholarship.

  • 1.    PENDAHULUAN

Pendidikan adalah usaha sadar dan terencana untuk mewujudkan suasana belajar dan proses pembelajaran agar peserta didik secara aktif mengembangkan potensi dirinya untuk memiliki kekuatan spiritual keagamaan, pengendalian diri, kepribadian, kecerdasan, akhlak mulia, serta ketrampilan yang diperlukan dirinya, masyarakat, bangsa dan negara (Pasal 1 UU Nomor 20 Tahun 2003). Di Indonesia, pembelajaran pada tingkat Perguruan Tinggi masih dikenakan biaya perkuliahan berdasarkan kemampuan ekonomi keluarga atau sesuai dari kebijakan masing-masing perguruan tinggi. Pemerintah telah mengupayakan pendanaan untuk membantu masyarakat ekonomi rendah dan berprestasi agar dapat melanjutkan studi di perguruan tinggi melalui penyaluran beasiswa, salah satunya adalah beasiswa bidikmisi.

Universitas Udayana menjadi salah satu Perguruan Tinggi Negeri yang dipercaya untuk menyalurkan beasiswa bidikmisi sejak tahun 2010. Mahasiswa pelamar bidikmisi mengikuti proses verifikasi dan wawancara yang bertujuan untuk mengklasifikasi pelamar bidikmisi divisitasi atau tidak divisitasi. Pengklasifikasian pelamar bidikmisi ditentukan oleh Tim Verifikasi yang dibentuk oleh Rektor. Adapun

pelamar bidikmisi dinyatakan layak mendapatkan bidikmisi tanpa visitasi apabila data yang dilampirkan memenuhi persyaratan sebagai penerima bidikmisi. Sedangkan pelamar bidikmisi dinyatakan layak mendapat bidikmisi dengan visitasi apabila terdapat data yang tidak memenuhi syarat sebagai penerima bidikmisi.

Setiap Perguruan Tinggi memiliki kriteria sendiri berdasarkan Pemerintah Daerah yang disesuaikan dengan kondisi geografis Perguruan Tinggi dan kondisi ekonomi masyarakat setempat. Program bidikmisi menerapkan tiga prinsip utama yaitu tepat sasaran, tepat jumlah, dan tepat waktu.

Berdasarkan hal tersebut akan dilakukan penelitian untuk mengklasifikasi pelamar bidikmisi layak mendapat bidikmisi dengan visitasi atau tanpa visitasi berdasarkan jumlah gabungan pendapatan orang tua, pendapatan orang tua dibagi jumlah tanggungan keluarga, luas tanah, luas bangunan, bantuan dari pemerintah, dan tagihan listrik. Hal ini perlu dikaji agar beasiswa bidikmisi yang diberikan dapat memenuhi prinsip pertama yaitu tepat sasaran. Untuk pengklasifikasian pelamar bidikmisi dapat menggunakan metode statistika yaitu analisis diskriminan dan regresi logistik.

Analisis diskriminan merupakan suatu metode statistika yang digunakan untuk mengklasifikasi suatu individu atau objek ke dalam suatu kelompok yang telah ditentukan sebelumnya berdasarkan variabel-variabel bebasnya (Dillon & Goldstein, 1984). Tujuan analisis diskriminan adalah membentuk sejumlah fungsi melalui kombinasi linier dari variabel bebasnya yang digunakan untuk memisahkan kelompok individu tersebut dan mengklasifikasi individu baru ke dalam salah satu kelompok (Hair et al, 2010). Sampel yang digunakan pada analisis diskriminan sebaiknya dibedakan menjadi dua yaitu, analysis sample (data analisis) yang digunakan untuk membentuk fungsi diskriminan dan holdout sample (data validasi) yang digunakan untuk menguji ketepatan dari fungsi diskriminan yang telah dibentuk. Analisis diskriminan memiliki asumsi utama yang harus dipenuhi yaitu data peubah berdistribusi normal ganda dan kehomogenan matriks ragam-peragam antar kelompok.

Regresi logistik merupakan salah satu model pendekatan yang digunakan untuk menganalisis hubungan satu atau beberapa variabel bebas dengan sebuah variabel terikat berupa kategori yang bersifat dikotomi atau biner. Menurut Hosmer dan Lameshow (2000), analisis regresi logistik merupakan metode regresi dengan variabel terikat kategorik atau dikotomi dan variabel bebasya merupakan kategorik dan atau kontinu. Tujuan dari regresi logistik adalah memperkirakan besarnya probabilitas kejadian tertentu di dalam suatu populasi. Asumsi-asumsi regresi logistik yang harus dipenuhi antara lain, variabel terikat harus bersifat dikotomi, variabel bebas tidak harus memiliki keragaman yang sama antar kelompok, tidak mengasumsikan hubungan linier antara variabel terikat dan variabel bebas, variabel bebas tidak memerlukan asumsi kenormalan ganda, kategori dalam variabel bebas harus terpisah satu sama lain.

Berdasarkan pemaparan yang telah diuraikan sebelumnya, maka dalam penelitian ini dilakukan perbandingan kedua metode tersebut yaitu analisis diskriminan dan regresi logistik untuk mengklasifikasi pelamar bidikmisi berdasarkan ketepatan pengklasifikasiannya menggunakan nilai Apparent Error Rate (APER). APER merupakan nilai dari besar kecilnya jumlah observasi yang salah dalam pengklasifikasian berdasarkan suatu fungsi klasifikasi. Sehingga

diperoleh tingkat ketepatan pengklasifikasian berdasarkan nilai APER.

  • 2.    METODE PENELITIAN

    • 2.1.    Jenis dan Sumber Data

Jenis data yang digunakan berupa data kuantitatif dan kualitatif. Sumber data yang digunakan berupa data sekunder yang diperoleh dari Biro Administrasi Kemahasiswaan, Bagian Kesejahteraan Mahasiswa (BKM) Universitas Udayana.

  • 2.2.    Variabel Penelitian

Variabel yang digunakan dalam penelitian terdiri dari satu variabel terikat berupa kategorik dan enam variabel bebas berskala kontinu.

Tabel 2.1 Variabel Penelitian

No

Variabel

Skala Pengukuran

Kategori

1.

Kelayakan

Visistasi Pelamar Bidikmisi

Nominal

  • 1:    Tidak

  • 2:    Ya

2.

Pendapatan Gabungan Orang Tua

Rasio

-

3.

Pendapatan Orang Tua dibagi Jumlah Tanggungan Keluarga

Rasio

-

4.

Luas Tanah

Rasio

-

5.

Luas Bangunan

Rasio

-

6.

Bantuan dari Pemerintah

Rasio

-

7.

Tagihan Listrik

Rasio

-

  • 2.3.    Tahap Analisis Data

Analisis data dalam penelitian ini menggunakan software R i386 3.4.3, IBM

SPSS Statistic 22, dan Microsoft Excel 2007. Berikut tahap analisi data yang dilakukan dalam penelitian ini:

  • 1.    Membagi data menjadi dua, yaitu data analisis yang digunakan untuk membentuk fungsi sebesar 80% dan data testing untuk pengujian ketepatan pengklasifikasian sebesar 20%.

  • 2.    Menganalisis data menggunakan metode analisis diskriminan dengan tahapan sebagai berikut:

  • a)    Melakukan uji distribusi normal ganda menggunakan plot nilai jarak mahalanobis

(di ) setiap pengamatan dan nilai khi-

kuadrat * Xp (  , -)+ (Johnson & Wichern

1998).

Hipotesis pengujiannya yaitu:

Hq : data berdistribusi normal ganda, Hy : data tidak berdistribusi normal ganda. Statistik uji:

d? =(Xi-̅)′s-1(Xi - ̅),    (2.1)

Keputusan uji:

Jika lebih dari 50% nilai di >X(,  , ) maka

kriteria keputusannya adalah tolak Hq , yang berarti data tidak berdistribusi normal ganda.

  • b)    Menguji kehomogenan matriks ragam peragam antar kelompok menggunakan uji Box’s M (Morrison, 1990).

Hipotesis pengujiannya yaitu:

^o :    =   ,

Hy :   ≠ ^2 (matriks ragam peragam kedua

kelompok tidak homogen).

Statistik uji:

M=-∑Li(ni-1) ln|S|-∑Li(ni-1)ln |Si|.

Keputusan uji:

Jika M> Z2.i

OL;(    )6(64^1)

(2.2)

maka


keputusannya adalah tolak Hq , yang berarti matriks ragam peragam kedua kelompok tidak homogen. Sehingga fungsi yang dibentuk adalah fungsi diskriminan kuadratik. Selanjutnya jika nilai M< Xl          kriteria keputusannya adalah

CC ; (2 — 1)6(6+1)         py

terima Hq , yang berarti matriks ragam peragam kedua kelompok homogen. Sehingga dibentuk fungsi diskriminan linier.

  • c)    Menguji kesamaan vektor nilai rata-rata menggunakan uji Wilks′ lambda.

Hipotesis pengujiannya yaitu:

¾: = , ^i : ≠ ^2 .

Statistik uji:

Wilks′ lambda=| | -|.       (2.3)

Keputusan uji:

Jika nilai P- value <a (0,05) maka kriteria keputusannya adalah tolak Hq , yang berarti terdapat perbedaan rata-rata dalam kelompok.

  • d)    Memilih variabel menggunakan metode stepwise, dengan kriteria variabel yang dipilih berdasarkan nilai F hitung terbesar, nilai WilksrIambda terkecil, dan nilai signifikansi variabel kurang dari a(0,05).

e) Membentuk fungsi diskriminan dan aturan pengklasifikasian. Jika fungsi diskriminan yang dibentuk adalah fungsi diskriminan linier, maka fungsi yang dapat dibentuk dari dua kelompok adalah satu fungsi. Aturan pengklasifikasian diskriminan linier untuk dua kelompok menggunakan titik tengah (optimum   cutting   score)(Johnson   &

Wichern, 2007):

̂=I[ ̅+ ̅ ],             (2.4)

dengan ̅ merupakan rata-rata dari fungsi diskriminan kelompok 1, dan ̅ adalah rata-rata fungsi diskriminan kelompok 2. Aturan pengklasifikasian menggunakan titik tengah dilakukan dengan syarat ̅> ̅ : xo diklasifikasikan ke kelompok 1, jika:

̂(xo)=̂,Xq ≥ ̂,        (2.5)

selainnya diklasifikasikan ke kelompok 2. Jika fungsi diskriminan yang dibentuk adalah fungsi diskriminan kuadratik, maka masing-masing kelompok mempunyai fungsi. Aturan pengklasifikasian untuk dua kelompok dilakukan dengan:

d® (X) = maksimum {d® (x), d® (X)}, (2.6) dengan d® (x) adalah fungsi diskriminan kuadratik kelompok 1 dan d-2 (X) merupakan fungsi diskriminan kuadratik kelompok 2. Pengamatan baru dimasukkan ke dalam kelompok yang memiliki skor diskriminan kuadratik terbesar.

  • f)    Memprediksi pengelompokan data validasi berdasarkan aturan klasifikasi yang telah dibentuk.

  • g)    Menghitung ketepatan klasifikasi fungsi diskriminan berdasarkan nilai Apparent Error Rate (APER).

  • h)    Menguji keakuratan dari pengklasifikasian fungsi diskriminan menggunakan uji Press’s Q (Hair et al, 2010).

Hipotesis pengujiannya yaitu:

Hq : pengklasifikasian akurat, Hy : pengklasifikasian tidak akurat. Statistik uji:

σ ,         [JV-(n×k)]2 .∏ 7λ

Press s =           .(2.7)

γ       N(k—1)..

Keputusan uji:

Jika nilai Press’s C>x(a;1) maka kriteria keputusannya adalah terima Hq , yang berarti pengklasifikasian dari fungsi diskriminan akurat.

  • 3.    Menganalisis data penelitian menggunakan metode regresi logistik dengan tahapan seperti berikut:

  • a)    Melakukan pengujian signifikansi parameter secara simultan menggunakan statistik uji G (Hosmer & Lameshow, 2000).

Hipotesis pengujiannya yaitu:

Hq :   =   =⋯=   =0, (tidak terdapat

pengaruh variabel bebas secara simultan terhadap variabel terikat),

: Minimal terdapat satu βj≠0, dengan j=1,2…,6 (terdapat pengaruh variabel bebas secara simultan terhadap variabel terikat).

Statistik uji:

G=-2In ^        (2.8)

Keputusan uji:

Jika nilai uji G>X(, ) maka kriteria keputusannya adalah tolak Hq , yang berarti terdapat pengaruh variabel bebas secara simultan terhadap variabel terikat.

  • b)    Menguji signifikansi parameter secara parsial menggunakan statistik uji Wald (Hosmer & Lameshow, 2000).

Hipotesis pengujiannya yaitu:

Hq :    =0 dengani=1,2,…,6 (variabel

bebas ke- j tidak mempunyai pengaruh yang signifikan terhadap variabel terikat)

Hy :    ≠0 denganj =1,2,…,6 (variabel

bebas ke- j mempunyai pengaruh yang signifikan terhadap variabel terikat).

Statistik uji:

w =[Se ( ̂ ; )]            (2.9)

Keputusan uji:

Jika nilai uji W>X(, ) maka keputusannya adalah tolak Hq , yang berarti variabel bebas mempunyai pengaruh signifikan terhadap variabel terikat.

  • c)    Menguji kesesuaian model dengan  uji

Hosmer  and Lameshow (Hosmer  &

Lameshow, 2000).

Hipotesis pengujiannya yaitu:

Hq: model dapat menjelaskan data secara layak,

Hy: model tidak dapat menjelaskan data secara layak.

Statistik uji:

  • ̂=∑ ^l (  _  ; ̅i ) .      (2.10)

  • '           ̅ir (1- ̅lr)

Keputusan uji:

Jika nilai uji ̂>X(,    ) maka kriteria

keputusannya adalah tolak Hq yang berarti model tidak dapat menjelaskan data secara layak.

  • d)    Mengestimasi parameter menggunakan metode kemungkinan maksimum (Hosmer & Lameshow, 2000).

  • e)    Memilih variabel menggunakan metode stepwise, dengan kriteria variabel yang masuk dalam model adalah memiliki pengurangan nilai -2 Log Iikeliℎood terbesar, koefisisen Wald terbesar, dan signifikansi variabel kurang dari a (0,05).

  • f)    Membentuk model regresi logistik dan aturan pengklasifikasiannya. Model regresi logistik dirumuskan dengan:

eβo+βlxl+β2x2 +⋯․

π( xi)=y+eβo+βlxl+β2x2 +⋯․     , (2.11)

dengan model transformasi logitnya yaitu:

Iogit =ln(:)=βo + βιxι+⋯․+βk%k .

(2.12) Aturan pengklasifikasian menggunakan nilai cut-off sebesar 0,5.

  • g)    Memprediksi pengelompokan data validasi berdasarkan aturan klasifikasi.

  • h)    Menghitung ketepatan klasifikasi fungsi regresi logistik berdasarkan nilai Apparent Error Rate (APER).

  • 4.    Menginterpretasi hasil analisis diskriminan dan regresi logistik.

  • 5.    Membandingkan ketepatan pengklasifikasian antara analisis diskriminan dan regresi logistik.

  • 3.    HASIL PEMBAHASAN

    • 3.1    Analisis Deskriptif

Statistika deskriptif dari data pelamar beasiswa bidikmisi di Universitas Udayana yang diterima melalui jalur Seleksi Nasional Masuk Perguruan Tinggi Negeri (SNMPTN) tahun 2018 ditunjukkan pada Tabel 3.1.

Berdasarkan Tabel 3.1, pelamar bidikmisi terbanyak di Universitas Udayana jalur SNMPTN tahun 2018 berasal dari Fakultas Matematika dan Ilmu Pengetahuan Alam yang berjumlah 36 mahasiswa. Sedangkan pelamar bidikmisi paling sedikit berasal dari Fakultas Hukum dan Fakultas Kedokteran Hewan yang berjumlah 11 mahasiswa. Setiap fakultas terdapat mahasiswa pelamar bidikmisi yang di visitasi. Adapun jumlah pelamar bidikmisi yang paling banyak di visitasi berasal dari Fakultas Ekonomi Bisnis dan Fakultas Kedokteran.

Tabel 3.1 Statistika Deskriptif Pelamar Bidikmisi UNUD Jalur SNMPTN Tahun 2018

Fakultas

Jumlah

Total

Tanpa Visitasi

Visitasi

Peternakan

10

4

14

Ekonomi dan Bisnis

26

8

34

Hukum

9

2

11

Ilmu Budaya

29

3

32

Ilmu Sosial dan Politik

11

1

12

Kedokteran

22

8

30

Kedokteran Hewan

10

1

11

Kelautan dan Perikanan

15

2

17

MIPA

34

2

36

Pertanian

28

2

30

Pariwisata

13

1

14

Teknik

21

3

24

Teknologi Pertanian

13

2

15

241

39

280

Sumber: Data diolah, 2019

Data penelitian ini dibagi menjadi dua yaitu data analisis sebesar 80% yang digunakan untuk membentuk fungsi klasifikasi dan data validasi sebesar 20% yang digunakan untuk menguji ketepatan fungsi klasifikasi yang dibentuk. Berdasarkan perhitungan, diperoleh 224 data untuk data analisis dan 56 data untuk data validasi.

  • 3.2    Analisis Diskriminan

Pada tahap ini, dilakukan analisis data pelamar bidikmisi di Universitas Udayana yang diterima melalui jalur SNMPTN tahun 2018 menggunakan metode analisis diskriminan.

  • 1)    Uji Distribusi Normal Ganda

Pengujian kenormalan ganda bertujuan untuk menilai sebaran data apakah berdistribusi normal ganda atau tidak. Pengujian dilakukan dengan plot jarak mahalanobis (di ) dan khi-kuadrat * Xv (, )+. Hipotesis pengujiannya yaitu:

Hq : data berdistribusi normal ganda,

H^ : data tidak berdistribusi normal ganda.

QQ-Plot Data Bidikmisi UNUD

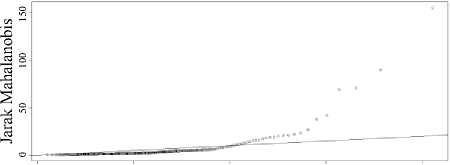
0                    5                   10                   15                   20

Khi-kuadrat

Berdasarkan Gambar 3.1, pencaran titik yang dibentuk mendekati garis lurus atau hasil plot berada di sekitar garis lurus, maka dapat disimpulkan data menyebar secara normal ganda. Jika menggunakan statistik uji, hasil perhitungan menunjukkan bahwa 21 data atau 9,375%       data       dengan       nilai

di >X(,  , )(12,59158). Sehingga kriteria

keputusannya adalah terima Hq , yang berarti data pelamar bidikmisi berdistribusi normal ganda.

  • 2)    Uji Kehomogenan Matriks Ragam

    Peragam

Pengujian asumsi kehomogenan matriks ragam peragam antar kelompok bertujuan untuk mengetahui matriks ragam peragam antar kelompok homogen atau tidak. Statistik uji yang digunakan adalah uji Box’s M, dengan rumusan hipotesis:

Hq :   = (matriks ragam peragam kedua

kelompok homogen),

H^ :   ≠ ^2 (matriks ragam peragam kedua

kelompok tidak homogen).

Hasil dari perhitungan menggunakan statistik uji Box’s M dapat dilihat pada Tabel 3.2:

Tabel 3.2 Hasil Uji Kesamaan Matriks Ragam Peragam dengan Uji Box’s M

Statistik Uji

Nilai

Boxʼs M               ∖

463,384

Sumber: Data diolah, 2019

Berdasarkan Tabel 3.2, hasil nilai Box’s M 463,384 > X(o,05;(2-1)6(6+1))(32,67), sehingga kriteria keputusannya adalah tolak Hq , yang berarti matriks ragam peragam kedua kelompok tidak homogen. Sehingga fungsi diskriminan yang dibentuk adalah fungsi diskriminan kuadratik.

  • 3)    Uji Vektor Nilai Rata-Rata

Pengujian vektor nilai rataan setiap variabel bebas dilakukan untuk menguji nilai rata-rata masing-masing kelompok dan mengetahui ada tidaknya perbedaan nilai rataan antar kelompok. Hipotesis yang digunakan yaitu:

^o :    = ,

^l :    ≠ ^2 .

Hasil pengujian vektor nilai rata-rata dapat dilihat pada Tabel 3.3:

Gambar 3.1 Plot Distribusi Normal Ganda


Tabel 3.3 Hasil Uji Vektor Nilai Rata-Rata (Tests of Equality of Groups Means)

Wilks’

Lambda

F

Sig.

Xl

0,486

234,709

0,000

χ2

0,647

121,109

0,000

χ2

0,999

0,185

0,667

X4

0,998

0,521

0,471

X5

0,993

1,661

0,199

X6

0,762

69,216

0,000

Sumber: Data diolah, 2019

Berdasarkan Tabel 3.3, jumlah gabungan pendapatan orang tua ( ^l), pendapatan orang tua dibagi jumlah tanggungan keluarga (X2), dan tagihan listrik (Xg) mempunyai nilai signifikansi kurang dari a(0,05), sehingga keputusannya adalah tolak Hq . Jadi dapat disimpulkan bahwa ketiga variabel tersebut memberikan perbedaan rata-rata pada pengelompokan kelayakan visitasi pelamar bidikmisi di Univeristas Udayana.

  • 4)    Pembentukan Fungsi Diskriminan

Pemilihan variabel diskriminan menggunakan metode stepwise dengan kriteria variabel yang memiliki nilai F terbesar, variabel yang memiliki nilai Wilksʼ lambda terkecil, dan variabel yang memiliki nilai signifikansi kurang dari a (0,05). Variabel bebas yang mendominasi pembentukan fungsi diskriminan dapat dilihat pada Tabel 3.4:

Tabel 3.4 Variabel yang Masuk Dalam Analisis Diskriminan

Step

Variabel

Wilks’ Lambda

F

Sig.

3

Xl

0,530

56,985

0,000

X6

0,460

20,496

0,000

χ2

0,449

14,988

0,000

Sumber: Data diolah, 2019

Berdasarkan Tabel 3.4, variabel yang masuk dalam pembentukan fungsi diskriminan yaitu jumlah gabungan pendapatan orang tua ( ^l), pendapatan orang tua dibagi jumlah tanggungan keluarga ( ¾ ), dan tagihan listrik (Xg).

Berdasarkan hasil uji asumsi yang telah dilakukan, data peubah memenuhi asumsi kenormalan ganda tetapi tidak memenuhi asumsi kehomogenan matriks ragam peragam antar kelompok. Sehingga fungsi diskriminan yang dibentuk adalah fungsi diskriminan kuadratik. Fungsi diskriminan kuadratik untuk kelompok 1 dan 2 dirumuskan dengan:

0                     1

d® (X) =ln(0,8616) - ln(19,55034)

  • -2(χ- ̅1)τsr1 (χ- ̅1),

^2 (X) =ln(0,1384) -1ln(11667,71)

  • -I(x- ̅2)rs2-1(X- ̅2).

  • 5)    Pengklasifikasian Analisis Diskriminan

Hasil prediksi pengelompokkan data validasi menggunakan fungsi diskriminan kuadratik dapat dilihat pada Tabel 3.5:

Tabel 3.5 Hasil Prediksi Data Validasi Menggunakan Fungsi Diskriminan Kuadratik

Pengamatan

Prediksi

Jumlah

Tanpa Visitasi

Visitasi

Tanpa

Visitasi

46

2

48

Visitasi

1

7

8

Jumlah

47

9

56

Sumber: Data diolah, 2019

Berdasarkan Tabel 3.5, dapat dihitung tingkat kesalahan klasifikasi menggunakan APER yaitu:

APER =   = 0,0536,

56

sedangkan ketepatan klasifikasi dari data validasi diperoleh:

(1 - 0,0536) = 0,9464 = 94,64%.

  • 6)    Uji Keakuratan Analisis Diskriminan

Uji keakuratan digunakan untuk menguji keakuratan dari pengklasifikasian yang dilakukan oleh fungsi diskriminan. Statistik uji yang digunakan adalah uji Press’s Q. Hipotesis yang digunakan yaitu:

Hq : pengklasifikasian akurat,

H1 : pengklasifikasian tidak akurat.

Berdasarkan perhitungan diperoleh nilai uji

Press’s Q (230,4143)>X(, ;1)(3,84146),

sehingga keputusannya adalah terima Hq , yang berarti hasil pengklasifikasian dari fungsi diskriminan kuadratik akurat.

  • 3.3    Regresi Logistik

Selanjutnya dilakukan analisis data pelamar bidikmisi di Universitas Udayana yang diterima melalui jalur SNMPTN tahun 2018 dengan metode regresi logistik.

  • 1)    Uji Signifikansi Parameter (Simultan)

Uji signifikansi parameter secara simultan atau serentak dilakukan untuk mengetahui

pengaruh parameter β terhadap variabel terikat secara keseluruhan. Uji yang digunakan adalah Uji G . Hipotesis pengujian yang digunakan yaitu:

Hq :  =   =⋯=   =0 (tidak ada pengaruh

variabel bebas secara simultan terhadap variabel terikat),

Hγ :Minimal terdapat satu βj≠0, dengan j=1,2…,6 (ada pengaruh variabel bebas secara simultan terhadap variabel terikat).

Hasil pengujian parameter secara simultan dapat dilihat pada Tabel 3.6:

Tabel 3.6 Hasil Pengujian Parameter Secara Simultan

Step

-2 Log \ Iikeliℎood \

Cox & Snell R Square

Nagelkerke R Square

1

43,054

0,458

0,828

Sumber: Data diolah, 2019

Berdasarkan Tabel 3.6, nilai uji G (43,054) > X(, ;6)(12,59159),       maka

keputusannya tolak Hq , yang artinya terdapat paling sedikit satu variabel bebas yang berpengaruh secara simultan terhadap variabel terikat.

  • 2)    Uji Signifikansi Parameter (Parsial)

Uji signifikansi parameter secara parsial dilakukan untuk menunjukkan suatu variabel bebas layak atau tidak untuk masuk kedalam model. Statistik uji yang digunakan adalah uji Wald. Hipotesis pengujian yang digunakan yaitu:

Hq :   = 0dengani =1,2,…,6 (variabel bebas

ke-i tidak mempunyai pengaruh signifikan terhadap variabel terikat),

Hy :    ≠0  denganj=1,2,…,6 (variabel

bebas

ke-j mempunyai pengaruh yang signifikan terhadap variabel terikat).

Hasil pengujian parameter secara parsial dapat dilihat pada Tabel 3.7:

Tabel 3.7 Hasil Pengujian Parameter Secara Parsial

Variabel

Wald

Sig.

12,598

0,000

9,785

0,002

0,507

0,476

*4

1,283

0,257

1,365

0,243

X6

7,875

0,005

Konstanta

25,979

0,000

Sumber: Data diolah, 2019

Berdasarkan Tabel 3.7, nilai uji Wald Xy , ^2 , dan Xb lebih besar dari nilai X(,  ;1)(3,841),

sehingga kriteria keputusannya adalah tolak Hq , yang berarti variabel bebas ¾ , X^ , dan Xq mempunyai pengaruh secara signifikan terhadap pengklasifikasian pelamar bidikmisi.

  • 3)    Uji Kesesuaian Model

Uji kesesuaian model digunakan untuk mengevaluasi kesesuaian model dengan data. Model yang digunakan harus memenuhi goodness of fit, yaitu terdapat kesesuaian antara data yang dimasukkan dalam model dengan data yang diamati. Statistik uji yang digunakan adalah uji Hosmer and Lameshow. Hipotesis yang digunakan dalam pengujian yaitu:

Hq : model dapat menjelaskan data secara layak, Hi : model tidak dapat menjelaskan data secara layak.

Hasil pengujian kesesuaian model dapat dilihat pada Tabel 3.8:

Tabel 3.8 Uji Kesesuaian Model Hosmer and Lameshow

Step

Khi-kuadrat

db

Sig.

1

2,719

8

0,951

Sumber: Data diolah, 2019

Berdasarkan Tabel 3.8, nilai uji Hosmer and Lameshow( ̂)2,719 < X(,  ;8)(15,50731),

sehingga kriteria keputusannya adalah terima Hq, yang artinya model dapat menjelaskan data secara layak.

  • 4)    Pembentukan Fungsi Regresi Logistik

Pemilihan variabel regresi logistik menggunakan metode stepwise, dengan kriteria variabel yang memiliki pengurangan nilai -2 Log Iikeliℎood terbesar, koefisisen Wald terbesar, dan variabel yang dimasukkan dalam model memiliki nilai signifikansi kurang dari a (0,05). Variabel bebas yang memenuhi kriteria tersebut dan masuk dalam pembentukan fungsi regresi logistik dapat dilihat pada Tabel 3.9:

Tabel 3.9 Hasil Prediksi Data Validasi

Menggunakan Fungsi Regresi Logistik

Variabel

B

Wald

Sig.

Exp (B)

*1

2,478

13,207

0,000

11,920

4,548

9,377

0,002

94,452

*6

0,013

7,669

0,006

1,013

Konstanta

-11,685

30,583

0,000

0,000

Sumber: Data diolah, 2019

Berdasarkan Tabel 3.9, model regresi logistik yang terbentuk dirumuskan dengan:

, .      e"11 ,685 + 2,478X1+4, 548X2 + 0,013X6

π(xi)=1+e-11 ,685 + 2,478X1 + 4,548X2+0,013X6 .

Dan model transformasi logitnya dirumuskan dengan:

9(xi) =-11,685+2,478Xi + 4,548X2 +0,013 *6 ,

dengan

^l : jumlah gabungan pendapatan orang tua,

^2 : pendapatan orang tua dibagi jumlah tanggungan keluarga,

^6 : tagihan listrik.

  • 5)    Pengklasifikasian Regresi Logistik

Hasil prediksi pengelompokkan data validasi menggunakan fungsi regresi logistik dapat dilihat pada Tabel 3.10:

Tabel 3.10 Hasil Prediksi Data Validasi

Menggunakan Fungsi Regresi Logistik

Pengamatan

Prediksi

Jumlah

Tanpa Visitasi

Visitasi

Tanpa

Visitasi

48

0

48

Visitasi

1

7

8

Jumlah

49

7

56

Sumber: Data diolah, 2019

Berdasarkan Tabel 3.10, dapat dihitung tingkat kesalahan klasifikasi menggunakan APER yaitu:

0+1

APER =     = 0,0179

56

Sedangkan ketepatan klasifikasi dari data validasi diperoleh:

(1 - 0,0179) = 0,9821 = 98,21%

  • 3.4    Perbandingan Hasil Analisis

    Diskriminan dan Regresi Logistik

Selanjutnya dilakukan perbandingan metode analisis diskriminan dan regresi logistik untuk mengklasifikasi pelamar bidikmisi di Universitas Udayana berdasarkan ketepatan klasifikasinya.     Perbandingan ketepatan

pengklasifikasian dua metode tersebut dapat dilihat pada Tabel 3.11:

Tabel 3.11 Hasil Perbandingan Ketepatan

Pengklasifikasian Analisis Diskriminan dan Regresi Logistik

Metode

Ketepatan Pengklasifikasian

Analisis Diskriminan

94,64%

Regresi Logistik

98,21%

Sumber: Data diolah, 2019

Ketepatan pengklasifikasian menggunakan metode analisis diskriminan sebesar 94,64%, sedangkan dengan regresi logistik sebesar 98,21% (Tabel 3.11). Hasil perbandingan ini menunjukkan ketepatan klasifikasi regresi logistik lebih tinggi dibanding analisis diskriminan.

  • 4.    KESIMPULAN DAN SARAN

Variabel bebas yang mempunyai pengaruh signifikan terhadap pengklasifikasian kelayakan visitasi pelamar bidikmisi Universitas Udayana menggunakan analisis diskriminan dan regresi logistik adalah jumlah gabungan pendapatan orang tua ( ^l), pendapatan orang tua dibagi jumlah tanggungan keluarga ( ^2), dan tagihan listrik ( Xe).

Hasil ketepatan klasifikasi menggunakan analisis diskriminan diperoleh sebesar 94,64%, sedangkan regresi logistik diperoleh sebesar 98,21%. Regresi logistik menghasilkan ketepatan klasifikasi yang lebih tinggi dibandingkan analisis diskriminan. Sehingga analisis yang lebih baik digunakan untuk mengklasifikasi kelayakan visitasi pelamar bidikmisi di Universitas Udayana adalah regresi logistik.

Untuk penelitian selanjutnya, disarankan untuk menggunakan variabel bebas dengan skala pengukuran diskrit atau kategorik. Kemudian untuk tahun 2020, beasiswa bidikmisi sudah tidak diberlakukan dan digantikan dengan Kartu Indonesia Pintar (KIP), sehingga disarankan untuk kedepannya agar dilakukan penelitian mengenai pengklasifikasian pelamar beasiswa Kartu Indonesia Pintar (KIP) berdasarkan faktor-faktornya.

DAFTAR PUSTAKA

Departemen Pendidikan Nasional. (2003).

Undang-Undang Nomor 20 Tahun 2003 tentang Sistem Pendidikan Nasional. Jakarta: Depdiknas

Dillon, W. R.,  & Goldstein, M. (1984).

Multivariate Analysis Methods and Application. United States of America: John Wiley & Sons.

Hair, J. F., Black, W. C., Babin, B. J., & Anderson, R. E. (2010). Multivariate Data Analysis (7th ed.). New Jersey: Pearson Prentice Hall.

Johnson, R. A., & Wichern. (1992). Applied Multivariate Statistical Analysis. New Jersey: Prentice hall.

Morrison, D. F. (1990). Multivariate Statistical Methods. New York: McGraw-Hill, Inc.

Hosmer, D. W., & Lameshow, S. (2000).

Applied Logistic Regression (2nd ed.). New York: John Wiley & Sons.

Kewirausahaan, S. K., Kemahasiswaan, D. P., & Kemristekdikti. (2018). Jejak Langkah Bidikmisi 2010-2018. Jakarta:   Ditjen

Belmawa Kemristekdikti.

22