METODE STATE SPACE DALAM MERAMALKAN JUMLAH PENUMPANG KERETA API DI PULAU JAWA
on
E-Jurnal Matematika Vol. 9(1), Januari 2020, pp.8-13
DOI: https://doi.org/10.24843/MTK.2020.v09.i01.p272
ISSN: 2303-1751
METODE STATE SPACE DALAM MERAMALKAN JUMLAH PENUMPANG KERETA API DI PULAU JAWA
Fitri Ananda Dita Saraswita1§, I Wayan Sumarjaya2, Luh Putu Ida Harini3
1Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: fitri.ananda53@gmail.com] 2Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: sumarjaya@unud.ac.id] 3Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: ballidah@gmail.com]
§Corresponding Author
ABSTRACT
State space is an approach to model and predict together several time series data that are interconnected, and these variables have dynamic interactions. The purpose of this research is to model the number of train passengers in Java and find out the forecasting results using the state space method. The algorithm used to solve the state space model is the Kalman filter. In this research, a suitable final model is local level model with seasonal and produces MAPE value of 2%, this shows that the state space method is very accurately.
Keywords: train passengers, forecasting, state space, Kalman filter.
Pada era globalisasi, perkembangan dalam bidang transportasi sangat pesat. Transportasi merupakan salah satu sarana yang penting bagi penduduk untuk melakukan aktivitasnya. Salah satu transportasi darat yang sangat diperlukan masyarakat yaitu kereta api. Keunggulan kereta api dibanding alat transportasi umum lainnya yaitu lebih ramah biaya, lebih nyaman, dan tidak macet. Oleh karena itu, kereta api merupakan alat transportasi antarkota yang diminati oleh seluruh lapisan masyarakat, baik kelas menengah ke atas maupun ke bawah.
Data pada Badan Pusat Statistik (2019) menunjukkan jumlah penumpang kereta api di Indonesia, khususnya di Pulau Jawa pada tahun 2006 sampai tahun 2018, sangat bervariasi dan tidak stabil setiap bulannya. Oleh karena itu, peramalan tentang jumlah penumpang kereta api sangat diperlukan oleh perusahaan untuk mengetahui prediksi jumlah penumpang kereta api pada periode berikutnya.
Peramalan merupakan perhitungan objektif yang menggunakan data-data masa lalu, untuk menentukan sesuatu pada masa yang akan datang (Sumayang, 2003:24). Data deret waktu adalah sekumpulan data hasil dari pengamatan historis yang menggambarkan secara kronologis suatu karakteristik populasi di mana kaitan variabel waktu dengan pengamatan
diperhatikan, sehingga data dianggap sebagai fungsi atas waktu (Gujarati, 2004:25). Sedangkan deret waktu adalah deretan data atau amatan yang terurut berdasarkan waktu tertentu, dengan ketentuan memiliki selang waktu yang sama (Wei, 2006:1).
Salah satu metode yang dapat digunakan dalam peramalan adalah metode state space. State space adalah pendekatan untuk memodelkan dan memprediksi secara bersama beberapa data deret waktu yang saling berhubungan, serta peubah-peubah tersebut memiliki interaksi yang dinamis. Model state space menggambarkan data deret waktu melalui variabel keadaan (state vector). State vector berisi ringkasan semua informasi dari nilai sebelumnya dan nilai sekarang dari suatu deret waktu yang sesuai dengan prediksi nilai yang akan datang (SAS Institute Inc, 2014).
Algoritme yang dapat digunakan untuk menyelesaikan model state space adalah Kalman filter. Adapun konsep Kalman filter terdiri dari dua tahapan yaitu tahap peramalan dan tahap pembaharuan (Welch & Bishop, 2006). Pada tahap peramalan dihasilkan nilai estimasi untuk keadaan (state) pada waktu sekarang dan nilai kovarians galat yang digunakan sebagai informasi estimasi awal untuk langkah selanjutnya. Sedangkan pada
tahap pembaharuan berfungsi sebagai pengoreksi. Pada tahap ini akan dihasilkan pengukuran baru yang diperoleh dari nilai estimasi awal. Setelah kedua tahap terpenuhi, proses tersebut akan berulang kembali dengan nilai estimasi yang diperoleh dari tahap pengukuran digunakan sebagai informasi awal tahap peramalan yang kedua, begitu seterusnya hingga diperoleh nilai yang konvergen.
Penelitian mengenai state space dilakukan oleh Saputra (2018) yang meramalkan ekspor batubara dan minyak bumi. Penelitian tersebut memperlihatkan aplikasi model state space cukup baik berdasarkan plot yang dihasilkan dengan nilai MAPE untuk batubara sebesar 3,21% dan untuk minyak bumi sebesar 6,09%. Sedangkan penelitian mengenai jumlah penumpang kereta api di Pulau Jawa dilakukan oleh Arianto (2017) yang meramalkan jumlah penumpang kereta api di Jawa pada periode Februari 2017 sampai Januari 2018 dengan menggunakan metode ARIMA, penelitian tersebut memperlihatkan model yang diperoleh yaitu ARIMA ([12],1,1) dengan jumlah penumpang tertinggi berada pada bulan Desember.
Pada penelitian ini penulis menggunakan metode state space untuk memodelkan dan mengetahui hasil peramalan jumlah penumpang kereta api di Pulau Jawa pada periode Februari 2018 sampai Januari 2019.
Jenis data yang digunakan pada penelitian ini adalah data sekunder yaitu data jumlah penumpang kereta api di Pulau Jawa pada Badan Pusat Statistik (BPS). Data ini diambil pada periode Januari 2006 sampai Januari 2018. Berikut merupakan laman resminya https://www.bps.go.id.
Pada penelitian ini, peneliti meramalkan jumlah penumpang kereta api untuk periode berikutnya menggunakan metode state space dengan bantuan software R. Adapun langkah-langkah yang dilakukan dalam penelitian ini adalah:
-
1. Plot data deret waktu
Plot data deret waktu dilakukan guna untuk menunjukkan secara deskriptif gambaran umum mengenai data.
-
2. Pemodelan state space
Pada langkah ini dilakukan pemeriksaan
diagnostik berdasarkan asumsi yang harus dipenuhi, yaitu asumsi kebebasan dengan didiagnosis menggunakan uji Ljung-Box. Hipotesis yang digunakan dalam pengujian asumsi kebebasan yaitu:
H0 : = = =⋯=0 (tidak ada
korelasi residual antar lag),
H^ :terdapat paling sedikit satu Pk≠0, =
-
1,2, …,ℓ (ada korelasi residual antar lag).
Asumsi kenormalan didiagnosis dengan menggunakan uji Shapiro-Wilk. Hipotesis yang digunakan dalam pengujian kenormalan yaitu:
Hq : data berdistribusi normal,
H^ : data tidak berdistribsi normal.
Dan asumsi homoskedastisitas dengan cara mengamati plot kuadrat residualnya (Koopman & Commandeur, 2015). Untuk pemodelan state space dimulai dari model paling sederhana yaitu local level model. Apabila ketiga asumsi tidak terpenuhi maka pemodelan dilanjutkan dengan local linear trend model, apabila ketiga asumsi tidak terpenuhi lagi maka pemodelan dilanjutkan ke local level model with seasonal.
-
3. Penerapan algoritme Kalman filter Tahap 1 : Initial state
Dalam tahap ini dimulai dengan mengasumsikan nilai dari rata-rata (a1) dan varians (P^ ) telah diketahui.
Tahap 2 : Tahap peramalan
Dalam tahap ini dilakukan dengan menghitung nilai at+ι dan P^+^ .
Tahap 3 : Tahap pembaharuan
Dalam tahap ini dilakukan pembaharuan nilai at | ^ dan Pt |f hingga diperoleh nilai yang konvergen.
Setelah tahap 1 sampai tahap 3 diperoleh, langkah selanjutnya yaitu menghitung nilai ̂t berdasarkan model yang diperoleh.
-
4. Kriteria peramalan
Setelah model diperoleh dan memenuhi asumsi kebebasan, kenormalan, dan homoskedastisitas, maka langkah
selanjutnya yaitu menghitung nilai MAPE untuk dapat mengetahui tingkat keakuratan hasil dari peramalan.
Pada tahap ini terlebih dahulu dilakukan plot data jumlah penumpang kereta api di Pulau
Jawa pada periode Januari 2006 sampai Januari 2018 dengan data sebanyak 145 data. Langkah ini dilakukan untuk menunjukkan secara deskriptif gambaran umum mengenai data. Hasil plot data jumlah penumpang kereta api di Pulau Jawa dapat dilihat pada Gambar 3.1.
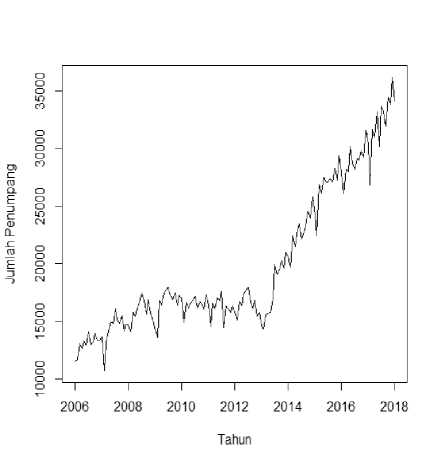
Gambar 3.1 Plot Data Jumlah Penumpang Kereta Api di Pulau Jawa
Hasil plot data jumlah penumpang kereta api di Pulau Jawa pada periode Januari 2006 sampai Januari 2018 menunjukkan pola yang berulang, sehingga dapat dikatakan bahwa adanya pola musiman yang memengaruhi pada data.
Pada tahap ini dilakukan pemilihan model berdasarkan asumsi yang harus dipenuhi, yaitu asumsi independence, normalitas, dan homoscedasticity. Untuk pemilihan model dimulai dari model yang paling sederhana yaitu local level model. Apabila ketiga asumsi tidak terpenuhi maka pemodelan dilanjutkan dengan local linear trend model, kemudian apabila ketiga asumsi tidak terpenuhi lagi maka pemodelan dilanjutkan dengan local level model with seasonal. Hasil diagnostik ketiga model ditunjukkan dalam Tabel 3.1.
Berdasarkan pada Tabel 3.1 untuk local level model menyatakan bahwa normality test menghasilkan P- value = 0,07599 > = 0,05. Karena P- value >a , maka kriteria keputusannya adalah terima Hq , yang artinya bahwa local level model memiliki sisaan yang berdistribusi normal, sehingga untuk asumsi normalitas terpenuhi. Sedangkan independence
test menghasilkan P- value=2,416× 10 5<a = 0,05. Karena P- value <a, maka kriteria keputusannya adalah tolak Hq , yang artinya bahwa terdapat korelasi residual antar lag pada local level model, sehingga asumsi independence tidak terpenuhi. Karena salah satu asumsi tidak terpenuhi, maka pemodelan dilanjutkan ke local linear trend model.
Tabel 3.1. Hasil Uji Normality dan Independence
|
P- value |
Normality test |
Independence test |
|
Local Level Model |
0,07599 |
2,416 × 10-≡ |
|
Local Linear Trend Model |
0,1244 |
2,056 × 10 ^8 |
|
Local Level Model with Seasonal |
0,0858 |
0,5787 |
Sumber: Data diolah (2019)
Kemudian untuk local linear trend model menyatakan normality test menghasilkan P- value = 0,1244 > a = 0,05. Oleh karena P- value >a, maka kriteria keputusannya adalah terima Hq , yang artinya bahwa local linear trend model memiliki sisaan yang berdistribusi normal, sehingga asumsi normalitas terpenuhi. Sedangkan untuk independence test menghasilkan P- = 2,056 × 10 -8 <a = 0,05. Karena P-value <a, maka kriteria keputusannya adalah tolak Hq , yang artinya bahwa terdapat korelasi residual antar lag pada local linear trend model, sehingga asumsi independence tidak terpenuhi. Karena salah satu asumsi tidak terpenuhi, maka pemodelan di lanjutkan ke local level model with seasonal.
Selanjutnya untuk local level model with seasonal menyatakan bahwa normality test menghasilkan P- value = 0,0858 > = 0,05. Karena P- value >a, maka kriteria keputusannya adalah terima Hq , yang artinya bahwa local level model with seasonal memiliki sisaan yang berdistribusi normal, sehingga asumsi normalitas terpenuhi. Sedangkan untuk independence test menghasilkan P- value = 0,5787 > = 0,05. Karena P- value >a, maka kriteria keputusannya adalah terima Hq , yang artinya bahwa tidak ada korelasi residual antar lag pada local level model with seasonal, sehingga asumsi independence juga terpenuhi.
Lebih lanjut, asumsi homoscedasticity dapat dilihat berdasarkan plot kuadrat residual
model data jumlah penumpang kereta api di Pulau Jawa pada Gambar 3.2.
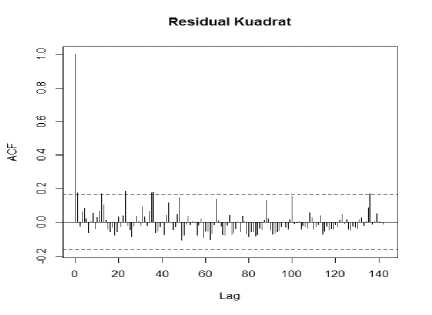
Gambar 3.2 Plot ACF (Autocorrelation Function) pada Kuadrat Residual.
Berdasarkan plot ACF pada Gambar 3.2 terlihat bahwa tidak adanya indikasi heteroskedastisitas yang ditunjukkan oleh beberapa lag yang keluar dari garis Bartlett. Oleh karena itu, dapat dikatakan sisaan pada model data penumpang kereta api bersifat homoskedastisitas.
Karena berdasarkan hasil uji asumsi kenormalan, kebebasan, dan homoskedastisitas yang memenuhi adalah local level model with seasonal, sehingga model akhir untuk data jumlah penumpang kereta api di Pulau Jawa yaitu local level model with seasonal. Selanjutnya local level model with seasonal untuk data bulanan jumlah penumpang kereta api di Pulau Jawa ditulis dengan:
̂ 't = ̂t+ ̂1,t
μt+1 = t
̂1,t+1 =- ̂1,t- ̂2,t- ̂3,t- ̂4,t- ̂5,t- ̂6,t-
̂7,t- ̂8,t- ̂9,t- ̂10,t- ̂11,t
y2,t+l = 1,t
y3,t+1 = 2,t
y-4,t + 1 = 3,t y5,t+1 = 4,t y6,t+1 = 5,t γ̂ 7,t+1 = γ̂ 6,t
γ̂ 8,t+1 = γ̂ 7,t
γ̂ 9,t+1 = γ̂ 8,t
y10,t+1 = 9,t y11,t+1 = 10,t
untuk t=1,…,n ; dengan Lh ~N(a1 , P^),
dimana α1 dan P^ diketahui. Nilai = 19908,84 dan Pl = 38252647. Selanjutnya
̂1 = 34459,16; ̂ , = -3095,7827;
-
̂2, 1 = -352,1559,; ̂3,1 = 1397,2770;
̂ , = -615,2570; ̂ , = 761,0342;
̂ , = 1032,3000; ̂ , = -844,4664;
̂10,1 = 1651,3231; ̂,11,1 = -431,9723;
Karena deret waktu yang diamati merupakan data bulanan pada jumlah penumpang kereta api di Pulau Jawa, sehingga
matriks CCf-, Rt, rIt, Ht , Pt ,Z t, Qt diperoleh
sebagai berikut:
zt = [1 1 0 0 0 0 0 0 0 0 00],
|
Ht = = 0,3577659, | ||||
|
F vt 1 |
10 | |||
|
Yi ,t⎤ |
01 | |||
|
⎢ |
/2 ,t |
⎢ |
00 | |
|
Y3 ,t |
00 | |||
|
Y4 ,t |
00 | |||
|
«t =⎢ |
Y5 ,t⎥ Y6 ,t⎥ |
, "■ = ⎢⎢ |
00 00 |
,m=[ ], |
|
⎢ |
Y7 ,t⎥ |
⎢ |
00 | |
|
⎢ |
Ys ,t⎥ |
⎢ |
00 | |
|
⎢ |
Y9 ,t⎥ |
⎢ |
00 | |
|
⎢ |
Yio,t⎥ |
⎢ |
00 | |
|
⎣Yn ,t⎦ |
⎣0 0⎦ | |||
1 D 0 0 0 0 D 0 0 0 0 D' 0 -1 -1 -1 -1 -, -1 -1 -1 -1 -1-1
,=000010000000 t= 0 0 0 0 0 1 0 0 0 0 00
■o Dooooooooid-
418759 0 000000000 0'
̂ , = -698,4130; ̂ , = 532,3999;
Nilai σε pada matriks Ht diperoleh dari varians residual pada model data penumpang kereta api ( Vt). Nilai σξ pada matriks Qt diperoleh dari varians residual pada rataan (μt). Kemudian untuk nilai σω pada matriks Qt diperoleh dari varians residual pada efek musiman ( Yt).
Setelah diperoleh model state space, tahap berikutnya adalah peramalan dengan menggunakan algoritme Kalman filter. Berikut hasil peramalan jumlah penumpang kereta api di Pulau Jawa untuk periode Februari 2018 sampai Januari 2019 pada Tabel 3.2.
Tabel 3.2. Hasil Peramalan Menggunakan Kalman filter
|
Tahun |
Bulan |
Hasil |
|
2018 |
Februari |
31.363 |
|
2018 |
Maret |
35.123 |
|
2018 |
April |
34.027 |
|
2018 |
Mei |
36.110 |
|
2018 |
Juni |
33.615 |
|
2018 |
Juli |
35.491 |
|
2018 |
Agustus |
34.992 |
|
2018 |
September |
33.761 |
|
2018 |
Oktober |
35.220 |
|
2018 |
November |
33.844 |
|
2018 |
Desember |
35.856 |
|
2019 |
Januari |
34.107 |
Sumber: Data diolah (2019)
Berdasarkan Tabel 3.2 terlihat bahwa jumlah penumpang tertinggi berada pada bulan Mei. Hal ini disebabkan pada bulan Mei merupakan bulan Ramadhan dan Hari Raya Idul Fitri, sehingga diperkirakan banyak masyarakat yang mudik lebaran. Kemudian, jumlah penumpang tertinggi kedua berada pada bulan Desember. Hal ini disebabkan pada bulan Desember merupakan Hari Raya Natal serta hari libur nasional, sehingga diperkirakan lonjakan jumlah penumpang kereta api juga terjadi pada bulan ini.
Sebagai suatu criteria dalam menguji ketepatan model, MAPE merepresentasikan model yang dibuat bahwa semakin kecil nilai MAPE, maka semakin baik model yang digunakan. Berikut hasil kekuatan peramalan
dari MAPE dinyatakan dalam Tabel 3.3.
Tabel 3.3 Kriteria Peramalan dengan Menggunakan MAPE
|
Yt |
̂ |
| Yt- ̂|×100% |
|
30.721 |
31.363 |
0,02091 |
|
35.272 |
35.123 |
0,004228 |
|
35.135 |
34.027 |
0,03153 |
|
34.877 |
36.110 |
0,035367 |
|
32.270 |
33.615 |
0,04167 |
|
36.089 |
35.491 |
0,016557 |
|
34.560 |
34.992 |
0,012487 |
|
33.878 |
33.761 |
0,003461 |
|
35.602 |
35.220 |
0,010724 |
|
34.637 |
33.844 |
0,022897 |
|
37.197 |
35.856 |
0,03604 |
|
34.435 |
34.107 |
0,009525 |
|
∑ MAPE |
2,044979 = 2% |
Sumber: Data diolah (2019)
Menurut Zhang et al. (2015), nilai MAPE yang kurang dari 10% menunjukkan bahwa peramalan sangat akurat. Sedangkan nilai MAPE antara 10% hingga 20% menunjukkan bahwa peramalan baik. Berdasarkan Tabel 3.3, diketahui bahwa nilai MAPE untuk data jumlah penumpang kereta api di Pulau Jawa sebesar 2,044979 atau 2%. Dengan demikian, dapat disimpulkan bahwa metode state space sangat akurat digunakan dalam meramalkan jumlah penumpang kereta api di Pulau Jawa.
Berdasarkan pembahasan pada bab sebelumnya, diperoleh model yang cocok untuk data jumlah penumpang kereta api di Pulau Jawa pada periode Januari 2006 sampai Januari 2018 adalah local level model with seasonal. Peramalan jumlah penumpang kereta api di Pulau Jawa untuk duabelas periode kedepan menggunakan algoritme Kalman filter dari bulan Februari 2018 sampai Januari 2019 diperoleh hasil secara berturut-turut, yaitu 31363; 35123; 34027; 36110; 33615; 35491; 34992; 33761; 35220; 33844; 35856; 34107. Dengan jumlah penumpang tertinggi berada pada bulan Mei dan nilai MAPE diperoleh sebesar 2%, sehingga peramalan jumlah penumpang kereta api dengan metode state space sangat akurat digunakan.
Pada penelitian ini hanya menggunakan state space linear Gaussian dalam meramalkan jumlah penumpang kereta api di Pulau Jawa, maka penelitian selanjutnya disarankan untuk menggunakan metode state space dengan noise (gangguan) yang lain.
DAFTAR PUSTAKA
Arianto, B Wicaksono. 2017. Peramalan Jumlah Penumpang Kereta Api di Pulau Jawa dan Sumatera Menggunakan Arima Box-Jenkins. Skripsi. Surabaya: Institut Teknologi Sepuluh Nopember.
Gujarati, D. 2004. Basic Econometrics. New York: McGraw-Hill.
Koopman, S. J., & Commandeur, J. J. 2015.
Time Series: State Space Methods.
International Encyclopedia of the Social & Behavioral Sciences.Vol.24 (354-360).
Saputra, Ramadhani. 2018. Kontruksi Model Peramalan dengan Menggunakan Metode State Space. Skripsi. Bandar Lampung: Universitas Lampung.
SAS Institute Inc. 2014. SAS/ETS User's Guide, Version 13.2. New York: SAS Institute Inc.
Sumayang, L. 2003. Dasar-Dasar Manajemen Produksi dan Operasi. Jakarta: Salemba Empat.
Wei, W. 2006. Time Series Analysis: Univariate and multivariate. New York: Pearson Addison Wesley.
Welch, G., & Bishop, G. 2006. An Introduction to the Kalman Filter. Chapel Hill: University of North Carolina.
Zhang, T., Wang, K., & Zhang, X. 2015. Modeling and Analyzing the Transmission Dynamics of HBV Epidemic in Xinjiang, China. Journal PLOS One, Volume 10, No.9, 1-14.
13
Discussion and feedback