E-Jurnal Matematika Vol. 8(4), November 2019, pp.309-315

DOI: https://doi.org/10.24843/MTK.2019.v08.i04.p270

ISSN: 2303-1751

PERAMALAN VOLATILITAS SAHAM MENGGUNAKAN MODEL EXPONENTIAL GARCH DAN THRESHOLD GARCH

Siti Rahayu Ningsih1§, I Wayan Sumarjaya2, Kartika Sari3

§Corresponding Author

ABSTRACT

In financial data there is asymmetric volatility, which denotes the different movements on conditional volatility of increase and decrease financial asset returns. The exponential GARCH and threshold GARCH models can be used to capture asymmetric volatility, called leverage effect. The aim of this research is to determine the best model between exponential GARCH and threshold GARCH models, and to know the results of forecasting volatility the LQ-45 stock index using the best model. The research showed that the best model to predicting volatility is EGARCH(2,1), because it has the smallest AIC value compared to other models. Then forecasting volatility of the LQ-45 stock index using EGARCH(2,1) showed that volatility increase from the first period until fourteenth period, this means that it has high volatility.

Keywords: Asymmetric, Exponential GARCH, Threshold GARCH, Volatility

GARCH memiliki respons volatilitas yang simetris terhadap guncangan positif (good news) maupun guncangan negatif (bad news). Namun, dalam beberapa kasus terdapat respons volatilitas yang bersifat asimetris (leverage effect), sehingga model GARCH dikembangkan dengan mengakomodasi adanya respons volatilitas yang bersifat asimetris, yaitu model exponential GARCH (EGARCH) oleh Nelson tahun 1991 dan model threshold GARCH (TGARCH) oleh Zakoian tahun 1994 (Tsay, 2013).

Model EGARCH dan TGARCH banyak diterapkan dalam pasar modal yaitu pada saham. Harga saham di bursa efek setiap saat dapat berubah-ubah, sehingga harga saham umumnya memiliki sifat heteroskedastik. Salah satu saham yang banyak dipilih adalah indeks saham LQ-45 karena dianggap memiliki kapitalisasi perdagangan yang paling aktif, sehingga sangat memengaruhi tingkat likuiditas dan tingkat pengembalian yang cepat bagi para trader (Sobirin, 2016).

Berdasarkan hal tersebut, adapun tujuan dari penelitian ini yaitu mengetahui model terbaik di antara model EGARCH dan TGARCH, serta

mengetahui hasil peramalan volatilitas indeks saham LQ-45 untuk periode 10 Juni 2019 hingga 27 Juni 2019.

  • 2.    METODE PENELITIAN

Data yang digunakan dalam penelitian ini adalah data sekunder, yaitu harga penutupan (closing price) indeks saham LQ-45 sejak tanggal 4 Maret 2013 sampai 31 Mei 2019 selama hari aktif (Senin sampai Jumat) yang diperoleh dari website resmi Yahoo Finance. Adapun langkah-langkah yang dilakukan adalah: 1. Menghitung return pada data harga indeks saham LQ-45.

rt =ln( -^)=lnPt -lnPt-I (1) Er t-l×

  • 2.    Menghitung skewness dan kurtosis data return untuk mengetahui apakah data indeks saham LQ-45 berdistribusi normal.

  • 3.    Melihat kestasioneran data return berdasarkan hasil pada langkah 1 melalui tampilan grafik correlogram dan melakukan pengujian dengan uji Augmented DickeyFuller (ADF) dengan hipotesis:

Hq ∶   =0 (data tidak stasioner),

H^ ∶   ≠0 (data stasioner).

Apabila data belum stasioner akan dilakukan proses differencing sampai diperoleh data yang stasioner.

  • 4.    Melakukan pemeriksaan pada residual kuadrat yang meliputi:

  • a.    Uji korelasi menggunakan uji Ljung-Box dan tampilan grafik correlogram, dengan hipotesis:

∏o ∶   =  =   =⋯=0     (tidak

terdapat korelasi pada residual),

H^ ∶ terdapat paling sedikit satu Pk ≠ 0, k=1,2,…ℓ (terdapat korelasi).

  • b.    Uji efek ARCH menggunakan uji ARCH-Lagrange  Multiplier dengan

hipotesis:

H0 ∶   =0; i=1,…,P (tidak ada efek

ARCH),

Hi ∶   ≠0;i=1,…,P (ada efek ARCH).

Jika tidak terdapat korelasi dan efek ARCH maka data tidak perlu dimodelkan menggunakan model GARCH dan proses berhenti.

  • 5.    Jika terdapat korelasi dan efek ARCH, maka dilakukan estimasi parameter model GARCH dengan menggunakan metode maximum likelihood estimation.

  • 6.    Menghitung nilai AIC, kemudian dipilih nilai AIC yang terkecil. Rumus umum AIC adalah:

AIC =  log(Iikeliℎood)+2F     (2)

  • 7.    Uji asimetris pada model GARCH terbaik menggunakan uji sign dan size bias. Jika tidak terdapat efek asimetris maka model yang digunakan adalah model GARCH. Jika terdapat efek asimetris, dilakukan estimasi parameter model EGARCH dan TGARCH menggunakan metode maximum likelihood estimation.

Model EGARCH( P,P) didefinisikan sebagai: ln tf =   +∑J=i 9 i (et-j)+

∑LiPt ln tf-i(3)

dengan

9i (et-j)=OCj ^t-j + Yj(|et-j|-E| et-j |),

j=1,…,Q .(4)

Kemudian, model   TGARCH( P,P)

didefinisikan sebagai:

tf =   +∑   ( «i + Yj^t-i) tf-i

+∑LiPitf-I(5)

dengan S^—^ adalah indikator untuk at-j , yaitu:

1   jikd &£—j<0

Et-ι ={0 jika cit—j≥0(6)

dan a0 merupakan konstanta, aj , Yj , Pi merupakan parameter model TGARCH (P,P), serta Yj merupakan efek asimetris pada waktu ke-j.

  • 8.    Menghitung nilai AIC model EGARCH dan TGARCH dan dipilih nilai AIC terkecil dari model EGARCH dan TGARCH.

  • 9.    Melakukan peramalan volatilitas saham untuk priode 10 Juni 2019 hingga 27 Juni 2019 dengan menggunakan model terbaik.

  • 3.    HASIL DAN PEMBAHASAN

    • 3.1    Analisis Deskriptif

Langkah pertama dalam penelitian ini adalah plot data harga penutupan (closing price) harian indeks saham LQ-45 dari tanggal 4 Maret 2013 sampai dengan 31 Mei 2019. Plot data ditunjukkan pada Gambar 1.

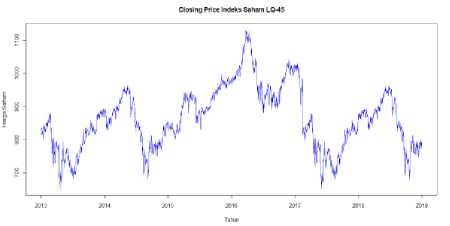
Gambar 1. Plot Closing Price Indeks Saham LQ-45

Berdasarkan Gambar 1 dilakukan analisis deskriptif, terlihat bahwa pergerakan harga berfluktuasi dari waktu ke waktu. Tampilan plot harga tersebut juga dapat digunakan untuk mengetahui data indeks saham LQ-45 telah stasioner atau tidak. Diketahui bahwa data tidak stasioner karena pada plot memperlihatkan adanya tren naik dan tren turun. Karena data indeks saham LQ-45 tidak stasioner maka akan dilakukan proses differencing dengan mencari nilai return.

Berdasarkan pada data indeks saham LQ-45, data harga saham pertama dan kedua secara berturut-turut adalah 814,920 dan 818,150, sehingga return pada periode pertama adalah:

814,920

r1 =ln , = -0,003955795 818,150 ,

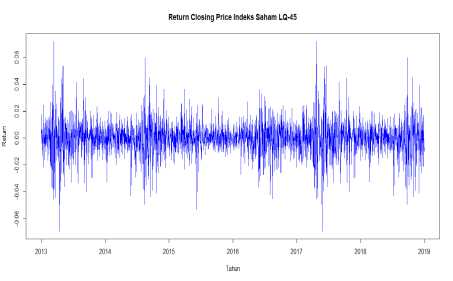
dengan cara yang sama dapat dihitung pula rt untuk t = 2, 3, … , 1.504. Dari sebanyak 1.504 observasi harga penutupan indeks saham LQ-45, diperoleh return sebanyak 1.503. Return indeks saham LQ-45 secara grafis ditunjukkan pada Gambar 2.

Gambar 2. Plot Return Indeks Saham LQ-45

Berdasarkan Gambar 2, terlihat bahwa pergerakan return sangat fluktuatif dari tahun ke tahun. Dalam teori keuangan atau finansial peristiwa ini disebut sebagai volatility clustering, yaitu kondisi dimana pergerakan data deret waktu (time series) cenderung naik atau turun secara drastis dan tiba-tiba dalam suatu kondisi atau kejadian tertentu (Tsay, 2013).

Kemudian, berdasarkan hasil statistik deskriptif dari data return diperoleh nilai mean positif yang mengindikasikan adanya peluang mendapatkan keuntungan. Kemudian diperoleh nilai deviasi standar mendekati nol, menunjukkan bahwa tidak terdapat perbedaan antara observasi harian indeks saham LQ-45 dengan nilai mean indeks saham.

Selanjutnya diperoleh nilai skewness negatif yang menunjukkan bahwa distribusi dari

return memiliki ekor kiri yang lebih panjang daripada ekor kanan distribusinya (long left tail), sehingga terdapat adanya ketidaksimetrisan dari distribusi normal. Dan nilai kurtosis lebih dari 3 sehingga terdapat adanya excess kurtosis. Excess kurtosis mengindikasikan bahwa return indeks saham LQ-45 memiliki kurva distribusi yang meruncing (leptokurtosis). Statistik deskriptif dari data return ditunjukkan pada Tabel 1.

Tabel 1. Statistik Deskriptif Return

Statistik Deskriptif

Nilai

Mean

0,000122

Deviasi Standar

0,012613

Skewness

-0,144574

Kurtosis

3,247764

Sumber: Data diolah, 2019

  • 3.2    Pemeriksaan Kestasioneran

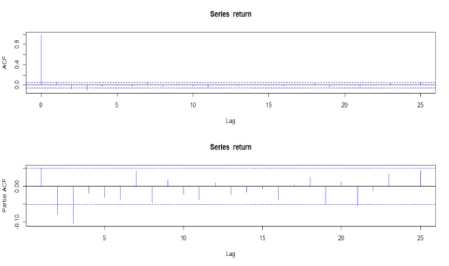
Berdasarkan Gambar 2, diketahui bahwa data return telah stasioner. Selanjutnya, untuk lebih memastikan bahwa data telah stasioner, dilakukan pengujian kestasioneran untuk data return dengan menggunakan tampilan grafik correlogram ACF dan PACF, serta uji Augmented Dickey Fuller (ADF). Tampilan grafik correlogram nilai ACF dan PACF ditunjukkan pada Gambar 4.

Gambar 4. Grafik Correlogram Nilai ACF dan PACF

Berdasarkan Gambar 4, terlihat bahwa hanya beberapa lag yang keluar dari garis Bartlet, sehingga dapat disimpulkan bahwa data return telah stasioner. Kemudian, dilanjutkan dengan uji Augmented Dickey Fuller (ADF) yang ditunjukkan pada Tabel 2.

Tabel 2. Hasil Uji Augmented Dickey Fuller

Augmented Dickey Fuller Test

t-statistic               -12,211

p-value                0,01

Sumber: Data diolah, 2019

Berdasarkan Tabel 2, diperoleh nilai statistik uji t sebesar -12,211 dan p-value sebesar 0,01 kurang dari taraf uji a = 5%, sehingga kriteria keputusannya adalah tolak H0 yang artinya data return stasioner.

  • 3.3    Uji Korelasi dan Uji Heteroskedastisitas

Korelasi dan heteroskedastisitas dapat diketahui dengan melakukan uji Ljung-Box dan uji ARCH-LM (Lagrange Multiplier) pada residual kuadrat dari return. Sebelum itu, terlebih dahulu dilihat tampilan grafik correlogram ACF pada residual kuadrat untuk mengetahui adanya korelasi pada data return yang ditunjukkan pada Gambar 5.

Series fi

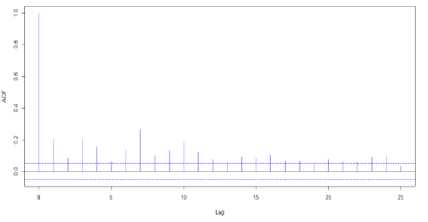
Gambar 5. Correlogram Nilai ACF Residual Kuadrat

Berdasarkan Gambar 5, diketahui bahwa sebagian besar lag pada correlogram melewati garis Bartlet. Hal ini berarti terdapat korelasi pada data return indeks saham LQ-45.

Kemudian dilanjutkan dengan pengujian menggunakan uji Ljung-Box untuk mengetahui keberadaan korelasi dan uji ARCH-LM untuk mengetahui keberadaan efek ARCH. Hasil perhitungan statistik uji Ljung-Box dan ARCH-LM dapat dilihat pada Tabel 3.

Tabel 3. Hasil Uji Ljung-Box dan Uji ARCH-LM

p-value

Ljung-Box                       < 2,2 × 10-16

ARCH Lagrange Multiplier     2,597 × 10-8

Sumber: Data diolah, 2019

Berdasarkan Tabel 3, untuk uji Ljung-Box diperoleh p-value sebesar < 2,2 × 10-16 kurang dari taraf uji a — 5%, sehingga kriteria keputusannya adalah tolak     yang artinya

terdapat korelasi pada residual kuadrat return. Selanjutnya, untuk uji ARCH-LM diperoleh p-value sebesar 2,597 × 10-8 kurang dari taraf uji

— 5%, sehingga kriteria keputusannya adalah tolak yang artinya terdapat efek ARCH pada residual kuadrat return. Karena terdapat

keberadaan korelasi dan efek ARCH maka perlu diakomodasi menggunakan model GARCH (P, Q ).

  • 3.4    Identifikasi Model GARCH

Hasil estimasi untuk masing-masing parameter dari model GARCH( , ) ditunjukkan pada Tabel 4.

Tabel 4. Estimasi Parameter GARCH(p, q)

Model

Parameter

Estimasi

Parameter

t-statistic

p-value

GARCH

α□

2,368 × 10-6

2,718

0,00656

(1,1)

α1

6,521 × 10-2

5,015

5,31 × 10-7

Λ

9,203 × 10-1

56,885

< 2 × 10-16

GARCH

α□

4,551 × 10-6

2,289

0,022074

(1,2)

α1

1,112 × 10-1

3,911

9,19 × 10-5

Λ

3,527 × 10-1

2,207

0,027303

β2

5,077 × 10-1

3,588

0,000333

GARCH

a0

2,369 × 10-6

2,708

0,00677

(2,1)

α1

6,521 × 10-2

2,753

0,00591

«2

1,000 × 10-8

0,000

1,00000

Λ

9,203 × 10-1

55,163

< 2 × 10-16

GARCH

a0

4,551 × 10-6

NA

NA

(2,2)

α1

1,112 × 10-1

4,926

8,41 × 10-7

«2

1,000 × 10-8

NA

NA

Λ

3,527 × 10-1

NA

NA

Pz

5,077 × 10-1

NA

NA

Sumber: Data diolah, 2019

Kemudian, dapat dilakukan pemilihan model terbaik menggunakan AIC (Akaike Information Criterion). Hasil perhitungan nilai AIC ditunjukkan pada Tabel 5.

Tabel 5. Nilai AIC Model GARCH (p, q )

Model

Nilai AIC

GARCH(1,1)

-6,090283

GARCH(1,2)

-6,092676

GARCH(2,1)

-6,088896

GARCH(2,2)

-6,091345

Sumber: Data diolah, 2019

Berdasarkan Tabel 4, diperoleh model dengan parameter yang signifikan adalah model GARCH(1,1) dan GARCH(1,2). Namun, berdasarkan Tabel 5 diperoleh model dengan nilai AIC terkecil yaitu pada model GARCH(1,2). Model GARCH(1,2) tidak melanggar asumsi non-negativity constraint, sehingga dapat digunakan untuk melakukan peramalan. Berdasarkan Tabel 4 diperoleh persamaan model GARCH(1,2), yaitu:

σt2 — 0,000004551 + 0,112 a?_1 + 0,3527 σt2. 1

+0,5077 σt2- 2

  • 3.5    Uji Sign dan Size Bias

Untuk mengetahui apakah terdapat pengaruh asimetris, terlebih dahulu data dimodelkan ke model GARCH dan diambil residualnya. Hasil dari uji sign dan size bias pada model GARCH(1,2) ditunjukkan pada Tabel 6.

Tabel 6. Uji Sign dan Size Bias

t-statistic

p-value

Sig

Sign Bias

0,1571

0,87515

Negative Size Bias

2,1396

0,03254

**

Positive Size Bias

1,0805

0,28009

Joint Effect

10,2413

0,01662

**

Sumber: Data diolah, 2019


Berdasarkan Tabel 6 terdapat beberapa parameter yang signifikan yaitu negative size bias dan joint effect, sehingga kriteria keputusannya adalah tolak Hq yang berarti residual model GARCH(1,2) bersifat asimetris. Karena terdapat efek asimetris pada model GARCH(1,2) maka dapat dimodelkan ke model EGARCH dan TGARCH.

  • 3.6    Estimasi Parameter Model EGARCH

    dan TGARCH

Hasil dari estimasi pada masing-masing parameter model EGARCH dan TGARCH ditunjukkan pada Tabel 7.

Tabel 7. Estimasi Parameter Model EGARCH dan TGARCH

Model

Parameter

Estimasi

Parameter

t-statistic

p-value

EGARCH

«0

-0,145603

-9,172748

0,000000

(1,1)

«1

-0,068471

-3,279291

0,001041

ft

0,983151

653,661953

0,000000

/1

0,098873

17,473811

0,000000

EGARCH

«0

-0,207700

-5,393735

0,000000

(1,2)

-0,094735

-5,786996

0,000000

ft

0,588038

498,867421

0,000000

ft

0,387953

241,076715

0,000000

/1

0,138268

5,493413

0,000000

EGARCH

«0

-0,129442

-61,97206

0,000000

(2,1)

-0,158571

-4,41841

0,000010

«2

0,100623

2,77523

0,005516

ft

0,985003

12914,4842

0,000000

/1

0,147083

4,52703

0,000006

y2

-0,050276

-2,50060

0,012398

EGARCH

«0

-0,127947

-3,5187

0,000434

(2,2)

-0,159485

-4,5746

0,000005

«2

0,102581

3,0085

0,002625

ft

1,000000

2,1492

0,000000

ft

-0,014819

-3,5904

0,000330

/1

0,147465

4,8147

0,000001

y2

-0,051896

-2,1411

0,032263

TGARCH

«0

1,938 × 10-4

3,944

8,01 × 10-5

(1,1)

α1

5,027 × 10-2

5,256

1,48 × 10-7

yi

7,315 × 10-1

3,829

0,000128

ft

9,460 × 10-1

99,104

< 2 × 10-16

Model

Parameter

Estimasi

Parameter

t-statistic

p-value

TGARCH

«0

2,769 × 10-4

3,557

0,000375

(1,2)

α1

6,993× 10-2

4,563

5,04 × 10-6

ft

7,299 × 10-1

3,816

0,000136

ft

5,295 × 10-1

3,034

0,002417

yi

3,947 × 10-1

2,365

0,018034

TGARCH

«0

1,935 × 10-4

3,948

7,88 × 10-5

(2,1)

5,012 × 10-2

5,252

1,50 × 10-7

«2

1,000 × 10-8

0,001

0,998991

ft

7,342 × 10-1

3,832

0,000127

yi

1,145 × 10-1

NA

NA

y2

9,462 × 10-1

99,361

< 2 × 10-16

TGARCH

«0

2,769 × 10-4

3,557

0,000375

(2,2)

6,993 × 10-2

4,563

5,04 × 10-6

«2

1,000 × 10-8

NA

NA

ft

7,299 × 10-1

3,816

0,000136

ft

-1,981 × 10-1

NA

NA

yi

5,295 × 10-1

3,034

0,002417

y2

3,947 × 10-1

2,365

0,018032

Sumber: Data diolah, 2019


Kemudian, dilakukan pemilihan model terbaik menggunakan AIC (Akaike Information Criterion). Hasil perhitungan nilai AIC ditunjukkan pada Tabel 8.

Tabel 8. Nilai AIC Model EGARCH dan TGARCH

Model

AIC

Model

AIC

EGARCH(1,1)

-6,1051

TGARCH(1,1)

-5,711828

EGARCH(1,2)

-6,1062

TGARCH(1,2)

2,903432

EGARCH(2,1)

-6,1089

TGARCH(2,1)

2,909223

EGARCH(2,2)

-6,1076

TGARCH(2,2)

2,906093

Sumber: Data diolah, 2019


Berdasarkan Tabel 7, diketahui bahwa semua model EGARCH signifikan. Namun, berdasarkan perhitungan nilai AIC pada Tabel 8 diperoleh model dengan nilai AIC terkecil pada model EGARCH(2,1). Kemudian, untuk model TGARCH diperoleh model yang signifikan pada model TGARCH(1,1) dan TGARCH(1,2). Namun, berdasarkan Tabel 8 diperoleh model dengan nilai AIC terkecil pada model TGARCH(1,1).

Selain itu berdasarkan nilai AIC terkecil dari model EGARCH dan TGARCH pada Tabel 8, diperoleh model terbaik untuk memodelkan efek asimetris pada indeks saham LQ-45 yaitu model EGARCH(2,1). Persamaan model EGARCH(2,1) berdasarkan hasil estimasi parameter pada Tabel 7 adalah:

ln σt2 =   + α⅛et-ι + ¾et-2 + Xi (| Et-ι|-E|Et-I|)

+/2 (| Et-2|-E| Et-2|)+βl ln σt-ι

= -0,129442 - 0,158571 Et-I + 0,100623Et-2 +0,147083(|Et-I|-E|Et-I |)

-0,050276(|Et-2|-E|Et-2|) -0,985003lnσt-l

Nilai -0,129442 merupakan parameter a0 dari model ARCH. Koefisien Ct1 bernilai negatif menunjukkan bahwa guncangan positif (good news) yang terjadi pada (t-1) memiliki efek yang lebih besar pada varians saat ini (σi). Sedangkan koefisien a2 bernilai positif, menunjukkan bahwa guncangan negatif (bad news) yang terjadi pada (t-2) memiliki efek yang lebih besar pada varians saat ini (σt ).

Kemudian, nilai parameter /1 dan γ2 tidak sama dengan nol, menunjukkan bahwa pada model EGARCH(2,1) terdapat adanya efek asimetris. Selanjutnya, nilai koefisien βγ bernilai positif dan signifikan secara statistik, artinya bahwa volatilitas pada saat ini tergantung dari volatilitas beberapa periode sebelumnya. Dan nilai koefisien βγ > 0,7, artinya old news mempunyai efek yang cukup persisten, atau dengan kata lain old news mempunyai pengaruh yang bersifat menetap pada volatilitas indeks saham LQ-45. Sehingga, indeks saham LQ-45 dapat dikatakan memiliki risiko ketidakpastian yang cukup tinggi (Sari, 2017).

  • 3.7    Peramalan Volatilitas

Hasil peramalan volatilitas indeks saham LQ-45 untuk periode 10 Juni 2019 hingga 27 Juni 2019 dengan menggunakan model EGARCH(2,1) ditunjukkan pada Tabel 9.

Tabel 9. Peramalan Volatilitas

No.

Tanggal

Hasil Peramalan

1

10 Juni 2019

0,01292

2

11 Juni 2019

0,01319

3

12 Juni 2019

0,01319

4

13 Juni 2019

0,01320

5

14 Juni 2019

0,01320

6

17 Juni 2019

0,01320

7

18 Juni 2019

0,01320

8

19 Juni 2019

0,01321

9

20 Juni 2019

0,01321

10

21 Juni 2019

0,01321

11

24 Juni 2019

0,01321

12

25 Juni 2019

0,01321

13

26 Juni 2019

0,01322

14

27 Juni 2019

0,01322

Sumber: Data diolah, 2019

Volatilitas indeks LQ-45 diramalkan selama 14 hari ke-depan, dikarenakan data indeks LQ-45 merupakan data finansial yang sering mengalami perubahan setiap saat. Oleh karena itu, untuk mendapatkan hasil peramalan yang tepat akan lebih baik apabila dilakukan peramalan dalam jangka waktu yang pendek yaitu selama 14 hari ke-depan.

Berdasarkan hasil peramalan, diketahui bahwa nilai volatilitas pada periode pertama sebesar 0,01292 yang menunjukkan bahwa perubahan indeks harga saham sebesar 0,01292. Kemudian, hasil peramalan volatilitas cenderung mengalami peningkatan dari periode pertama hingga periode ke empat belas. Selanjutnya, hasil peramalan volatilitas melebihi nilai deviasi standar dari return indeks saham LQ-45, sehingga dapat diketahui bahwa indeks saham LQ-45 memiliki volatilitas yang tinggi untuk 14 hari berikutnya.

Karena indeks saham LQ-45 memiliki volatilitas yang tinggi, maka menandakan bahwa terdapat risiko yang tinggi pula (Engle, 2001). Bagi investor yang menyukai risiko tinggi (risk takers) dapat mempertimbangkan untuk memilih saham-saham yang termasuk pada indek saham LQ-45.

  • 4.    SIMPULAN DAN SARAN

Setelah dilakukan analisis terhadap data return indeks saham LQ-45 diperoleh kesimpulan, yaitu:

Model terbaik yang diperoleh adalah model EGARCH(2,1) dengan persamaan

ln σ2 = + «iEt-i + ¾et-2 + Xi (| Et-i|-E|Et-I|)

+/2 (| Et-2|-E| Et-2|)+Pl ln Vt-I

= -0,129442 - 0,158571 et-l + 0,100623et-2 +0,147083(| ^t-I |-E|Et-I |)

-0,050276(|Et-2|-E|Et-2|) -0,985003lnσt2-ι

Hasil peramalan volatilitas indeks saham LQ-45 menggunakan model EGARCH(2,1) cenderung mengalami peningkatan dari periode pertama hingga periode ke empat belas yang menunjukkan bahwa indeks saham LQ-45 memiliki volatilitas yang tinggi.

Mengingat dalam penelitian ini hanya dilakukan pendekatan dengan model EGARCH dan TGARCH untuk meramalkan volatilitas indeks saham LQ-45, maka untuk penelitian selanjutnya disarankan untuk menggunakan model asimetris GARCH lainnya seperti APARCH, NGARCH, AVGARCH.

DAFTAR PUSTAKA

Engle, R., 2001. The Use of ARCH/GARCH Models in applied Econometrics. Journal of Econometrics Perspective, 15(4), pp. 157168.

Romli, H.,   2017. Faktor-faktor yang

Mempengaruhi Volatilitas Harga Saham Pada PT Waskita Karya Tbk. Jurnal Ilmiah Ekonomi Global Masa Kini, 8(1), pp. 1-5.

Sari, L. K., 2017. Pemodelan dan Transmisi Volatilitas Return Saham Utama Dunia Terhadap Indonesia. Skripsi. Institut Pertanian Bogor.

Sobirin, A., 2016. Penerapan Analisa Teknikal Untuk Memprediksi Pergerakan Harga Saham Pada Perusahaan LQ45 dengan Menggunakan Indikator RSI, MACD, Stochastic, Fibonacci dan Pivot Point. Skripsi. Universitas Wahid Hasyim Semarang.

Tsay, R., 2013. An Introduction to Analysis of Financial Data With R. New Jersey: John Wiley & Sons.

315