PERAMALAN JUMLAH KUNJUNGAN WISATAWAN MANCANEGARA KE BALI MENGGUNAKAN METODE SINGULAR SPECTRUM ANALYSIS
on
E-Jurnal Matematika Vol. 8(4), November 2019, pp.303-308
DOI: https://doi.org/10.24843/MTK.2019.v08.i04.p269
ISSN: 2303-1751
PERAMALAN JUMLAH KUNJUNGAN WISATAWAN MANCANEGARA KE BALI MENGGUNAKAN METODE SINGULAR SPECTRUM ANALYSIS
Mira Ayu Novita Sari1§, I Wayan Sumarjaya2, Made Susilawati3
1Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: miraayuns812@gmail.com] 2Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: sumarjaya@unud.ac.id] 3Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: mdsusilawati@unud.ac.id] §Corresponding Author
ABSTRACT
Singular spectrum analysis (SSA) is a method to decompose the original time series into a summation of a small number of components that can be interpreted as varied trends, oscillatory, and noise components. The purpose of this research is to model and to find out the results of forecasting the number of foreign tourists arrival to Bali using SSA method. In this research, the accuracy of forecasting results will be calculated using the SSA model with reccurent singular spectrum analysis (RSSA) method. The best SSA model was obtained with a window length (L=94) and produces MAPE value of 7,65%.
Keywords: singular spectrum analysis, reccurent singular spectrum analysis, foreign tourists arrival to Bali
Pariwisata memiliki peranan penting bagi masyarakat serta suatu negara. Pariwisata merupakan salah satu sektor penunjang pembangunan nasional sekaligus salah satu faktor penting untuk meningkatkan pendapatan masyarakat. Pariwisata juga telah ditetapkan sebagai leading sector oleh pemerintah Indonesia dan tercatat menduduki peringkat kedua penyumbang devisa terbesar setelah industri sawit. Kementerian Pariwisata (Kemenpar) mendata devisa yang diraup sektor pariwisata mencapai sembilan miliar dolar AS. Nilai tersebut didukung realisasi kunjungan wisatawan mancanegara yang terus tumbuh hingga akhir tahun 2018 ditarget mencapai tujuh belas juta orang (Anisa, 2019).
Pulau Bali merupakan salah satu daerah wisata di Indonesia yang sering dikunjungi oleh wisatawan mancanegara. Meskipun pariwisata di Bali sempat terguncang saat terjadi erupsi Gunung Agung, namun kini sudah mulai membaik. Hal ini ditunjukkan oleh kenaikan jumlah wisatawan mancanegara yang berkunjung ke Bali pada Januari 2019 (Assifa, 2019). Pada bulan tersebut sebanyak 463.285 wisatawan mancanegara datang ke Pulau Bali melalui Bandar Udara I Gusti Ngurah Rai.
Sedangkan pada periode yang sama pada tahun 2018 tercatat sebanyak 352.015 wisatawan. Hal tersebut dikatakan oleh General Manager PT Angkasa Pura I (Persero) Bandar Udara Ngurah Rai Bali melalui siaran pers (Assifa, 2019).
Saat ini Bali ditargetkan menyumbang minimal delapan juta kunjungan wisatawan mancanegara pada tahun 2019. Target delapan juta tersebut merupakan 40% dari target nasional yang membidik dua puluh juta wisatawan mancanegara pada 2019 (Mardika, 2019). Untuk mencapai target minimal ini tentu tidak terlepas dari perencanaan dan penyusunan strategi dalam meningkatkan sektor pariwisata. Untuk memperoleh gambaran capaian wisatawan mancanegara yang berkunjung ke Bali tahun 2019 diperlukan suatu metode peramalan. Peramalan jumlah kunjungan wisatawan mancanegara dan ketepatan analisis data deret waktu ini sangat bermanfaat bagi penetapan strategi peningkatan sektor pariwisata. Hal ini dikarenakan hasil ramalan jumlah kunjungan wisatawan mancanegara akan menentukan ke arah mana suatu kebijakan akan disusun.
Salah satu metode peramalan data deret waktu yang tengah berkembang saat ini adalah singular spectrum analysis (SSA). SSA adalah
teknik analisis deret waktu yang 3. mendekomposisi deret waktu asli menjadi suatu penjumlahan dari sejumlah kecil komponen yang independen dan dapat diinterpretasikan seperti komponen tren, musiman, dan noise (Golyandina et al., 2001).
Beberapa penelitian terkait metode SSA adalah sebagai berikut. Hassani (2007) melakukan perbandingan antara SSA, SARIMA, ARAR, dan Seasonal Holt-Winter dalam meramal data kematian akibat kecelakaan di USA pada tahun 1973. Hasil dari penelitian tersebut menyimpulkan bahwa SSA merupakan 4. metode terbaik yang bisa digunakan untuk melakukan peramalan dilihat dari nilai mean absolute error (MAE) dan mean relative absolute error (MRAE). Khaeri dkk (2017) menerapkan metode SSA pada peramalan jumlah penumpang kereta api di Indonesia tahun 2017 di mana ditunjukkan bahwa data memiliki lebih dari satu pola musiman. Hasil dari 5. penelitian tersebut menyimpulkan bahwa model SSA dapat meramalkan jumlah penumpang kereta api di Indonesia tahun 2017 dengan nilai MAPE sebesar 7,11%.
Pada penelitian ini penulis menggunakan metode SSA untuk memodelkan dan mengetahui hasil peramalan jumlah wisatawan mancanegara yang berkunjung ke Bali.
Jenis data yang digunakan dalam penelitian ini adalah data sekunder berupa data jumlah kunjungan wisatawan mancanegara ke Bali yang diperoleh dari Badan Pusat Statistik Provinsi Bali. Data yang digunakan adalah data bulanan dari periode Januari 1996 sampai Desember 2018. Data tersebut dibagi menjadi dua yaitu data in-sample (sebanyak 264 data yaitu data pada bulan Januari 1996 hingga Desember 2017) dan data out-sample (sebanyak 12 data yaitu data pada bulan Januari hingga Desember 2018).
2.2 Metode Analisis Data
6.
Menganalisis data menggunakan metode SSA diperlukan langkah-langkah sebagai berikut:
-
1. Mempersiapkan data jumlah kunjungan wisatawan mancanegara ke Bali periode 1996 - 2017.
-
2. Plot data untuk mengetahui karakteristik dan pola data.
7.
8.
Embedding
Pada langkah ini, deret satu dimensi digambarkan sebagai sebuah deret multidimensi yang dimensinya disebut window length (L). Menurut Hassani & Mahmoudvand (2018), pemilihan window length (L) dilakukan secara coba-coba N (trial and error) yang memenuhi 2≤L≤ dengan N = 264. Deret multidimensi
tersebut akan membentuk matriks lintasan X berukuran L×K dan K= -L+1.
Dekomposisi nilai singular (SVD)
Selanjutnya pada tahap SVD dilakukan dekomposisi nilai singular dari matriks lintasan X menjadi suatu penjumlahan dari matriks yang terbentuk dari eigentriple. Jadi, SVD dari matriks lintasan X dapat ditulis sebagai:
X= +⋯+xd dan Xj =√WiVl.
Pengelompokan
Langkah pengelompokan ini bertujuan untuk menentukan pola hasil dekomposisi ke dalam tiga pola umum dalam deret waktu yaitu tren, musiman, dan noise. Ada beberapa cara yang bisa digunakan untuk mengelompokkan komponen dari deret, yaitu:
-
a. Menggunakan grafik dari nilai singular. Suatu urutan grafik yang menurun secara perlahan atau lambat dari nilai singular biasanya terkait dengan komponen noise dari deret.
-
b. Memeriksa grafik satu dimensi dari deret yang direkonstruksi untuk mengidentifikasi komponen tren dan komponen musiman. Semua komponen yang bervariasi lambat pada grafik harus dikelompokkan ke dalam kelompok tren. Jika dua deret yang direkonstruksi oleh dua eigentriple yang berurutan menghasilkan pola musiman dan periode musiman yang sama, maka dua eigentriple tersebut dikelompokkan ke dalam kelompok musiman.
Melakukan diagonal averaging yang bertujuan untuk mengembalikan data menjadi deret sesuai dengan hasil pengelompokan tren dan musiman.
Melakukan peramalan menggunakan recurrent singular spectrum analysis (RSSA).
Menghitung tingkat kesalahan peramalan menggunakan nilai MAPE.
DOI: https://doi.org/10.24843/MTK.2019.v08.i04.p269
-
9. Melakukan interpretasi terhadap hasil peramalan dan menarik kesimpulan.
Proses analisis dilakukan dengan bantuan software R 3.4.4.
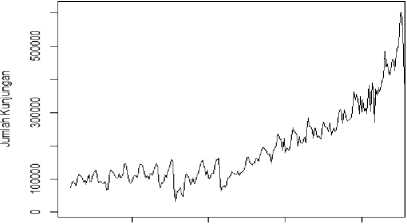
Bagian ini membahas penerapan metode singular spectrum analysis (SSA) untuk meramalkan jumlah kunjungan wisatawan mancanegara ke Bali. Berikut hasil plot data jumlah kunjungan wisatawan mancanegara ke Bali dari Januari 1996 sampai Desember 2017.
Jumlah KunjunganWisatawan Mancanegara ke Bali
2000 2005 2010 2015
Tahun
Gambar 1. Plot Data Jumlah Kunjungan Wisatawan Mancanegara ke Bali dari Januari 1996 sampai Desember 2017
Terlihat adanya pola tren naik pada data jumlah kunjungan wisatawan mancanegara ke Bali dari Januari 1996 hingga Desember 2017. Hal ini menunjukkan bahwa banyaknya wisatawan mancanegara yang berkunjung ke Bali mengalami peningkatan setiap tahun. Selain itu, terlihat adanya pola berulang pada data setiap tahun yang mengindikasikan adanya unsur musiman pada data.
Langkah pertama yang harus dilakukan pada tahap dekomposisi adalah embedding. Pertama dilakukan penentuan nilai window length (L) secara coba-coba (trial and error). Pada kasus ini banyak data yang digunakan adalah 264 data. Oleh karena itu nilai L yang memenuhi adalah 2≤L ≤ 132. Nilai L yang diambil setelah dilakukan proses coba-coba (trial and error) adalah L=94 dan K = 171. Nilai L yang dipilih didasarkan pada nilai MAPE minimum yaitu sebesar 7,64%. Dengan demikian matriks lintasan X dapat disusun sebagai berikut:
x=[Xl , X2,…, ^K]=(×i] ) , ,J 1
74124 87983 ⋯ 192579
87983 93380 ⋯ 184907
97385 83832 ⋯ 315909
Langkah selanjutnya dalam tahap dekomposisi adalah singular value
decomposition (SVD). Pada langkah SVD, matriks lintasan didekomposisi menjadi 50 eigentriple yang terdiri dari 50 nilai eigen dan 50 vektor eigen.
Terdapat dua langkah pada tahap rekonstruksi yaitu pengelompokan (grouping) dan diagonal averaging.
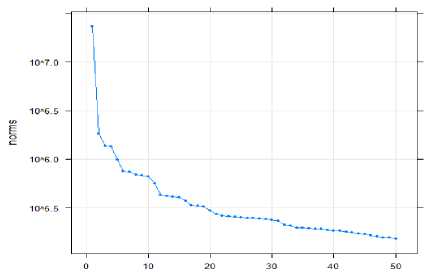
Langkah awal dalam tahap rekonstruksi adalah melakukan pengelompokan terhadap eigentriple yang berhubungan dengan tren, musiman, dan noise. Effect grouping (r) adalah parameter yang digunakan pada tahap pengelompokan untuk membatasi jumlah eigentriple yang akan digunakan pada proses identifikasi komponen tren dan musiman. Nilai parameter effect grouping (r) ditentukan berdasarkan jumlah eigentriple yang tidak mencerminkan noise pada plot nilai singular. Pada plot nilai singular, urutan nilai singular yang menurun secara lambat mencerminkan komponen noise.
Index
Gambar 2. Plot Nilai Singular
Gambar 2 menunjukkan plot nilai singular mulai menurun secara lambat dari eigentriple 20. Hal ini mengakibatkan eigentriple 20 hingga eigentriple 50 diidentifikasi sebagai komponen noise. Oleh karena itu ditentukan nilai parameter effect grouping (r) adalah r=19. Dengan demikian banyaknya eigentriple yang akan digunakan untuk mengidentifikasi komponen tren dan musiman adalah sembilan belas eigentriple. Dari sembilan belas eigentriple
pertama tersebut masih terdapat kemungkinan adanya eigentriple yang mencerminkan noise. Hal ini dapat diketahui dari sisa eigentriple yang tidak mencerminkan komponen tren dan musiman.
Banyaknya eigentriple yang akan digunakan untuk mengidentifikasi komponen tren dan musiman adalah sembilan belas eigentriple. Kesembilan belas eigentriple yang digunakan untuk mengidentifikasi komponen tren dan musiman terdiri dari eigentriple 1,2,3,…,19. Plot dari deret yang direkonstruksi dapat digunakan untuk mengidentifikasi eigentriple yang berhubungan dengan tren dan musiman.
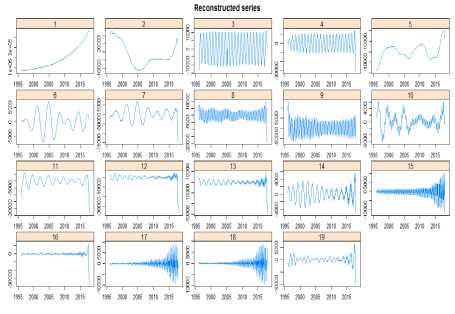
Gambar 3. Plot Deret yang Direkonstruksi
Plot deret yang direkonstruksi pada Gambar 3 memperlihatkan bahwa deret yang direkonstruksi oleh eigentriple 1 dan eigentriple 2 memuat komponen yang bervariasi lambat. Oleh karena itu, eigentriple 1 dan eigentriple 2 dikelompokkan ke dalam komponen tren. Selanjutnya pengelompokan terhadap eigentriple yang berhubungan dengan komponen musiman dilakukan berdasarkan kemiripan nilai singular dari eigentriple yang berurutan. Pada plot deret yang direkonstruksi, kemiripan nilai singular mengakibatkan deret yang direkonstruksi oleh suatu eigentriple memiliki pola dan periode musiman yang sama dengan deret yang direkonstruksi oleh eigentriple lainnya.
Pada Gambar 3 juga dapat diketahui bahwa terdapat beberapa pasang eigentriple berurutan yang memiliki kemiripan pola yaitu eigentriple 3 dan 4, eigentriple 6 dan 7, eigentriple 8 dan 9, eigentriple 12 dan 13, serta eigentriple 17 dan 18. Berdasarkan metode ESPRIT diketahui bahwa deret yang direkonstruksi oleh eigentriple 3 dan 4 memiliki periode musiman yang sama
yakni dua belas bulan sehingga dikelompokkan ke dalam komponen musiman. Selanjutnya, deret yang direkonstruksi oleh eigentriple 6 dan 7 memiliki periode musiman yang sama yakni 41 bulan. Meskipun deret yang direkonstruksi oleh eigentriple 6 dan 7 memiliki periode musiman yang sama, namun kedua eigentriple tersebut tidak dapat dikelompokkan ke dalam komponen musiman. Hal ini disebabkan oleh periode musiman kedua deret tersebut tidak dapat diinterpretasikan untuk data bulanan.
Selain melihat plot deret yang direkonstruksi, proses identifikasi eigentriple yang mencerminkan komponen tren dan musiman dapat dilihat pada plot keterpisahan (w-correlation). Plot keterpisahan (w-correlation) ini digunakan untuk melihat besarnya korelasi antar eigentriple. Semakin tua warnanya maka semakin tinggi korelasinya. Warna yang semakin muda keabu-abuan menunjukkan bahwa eigentriple tersebut memiliki kecenderungan sebagai noise.
W-correlation matrix

Gambar 4. Plot W-Correlation
Pada Gambar 4 dapat dilihat bahwa pasangan eigentriple 3 dan 4, 6 dan 7, 8 dan 9, 13 dan 14, serta 17 dan 18 memiliki korelasi yang kuat. Akan tetapi, untuk mengidentifikasi komponen musiman tidak dapat ditentukan hanya dengan melihat plot. Sehingga digunakan metode ESPRIT untuk mencari periode musiman dari deret yang direkonstruksi oleh dua eigentriple.
Tabel 1. Eigentriple dan Periode Musimannya
|
Eigentriple |
Periode |
Eigentriple |
Periode |
|
3 |
12 |
11 |
187 |
|
4 |
12 |
12 |
187 |
|
6 |
41 |
15 |
3 |
|
7 |
41 |
16 |
3 |
|
8 |
7 |
17 |
2 |
|
9 |
7 |
18 |
2 |
Sumber: Data diolah, 2019
Tabel 1 menyajikan secara lengkap pasangan eigentriple beserta periode musimannya. Diketahui bahwa pasangan eigentriple yang dapat dikelompokkan ke dalam kelompok musiman adalah eigentriple 3, 4, 15, 16, 17, dan 18.
Dengan demikian, eigentriple yang dikelompokkan ke dalam kelompok tren adalah eigentriple 1 dan 2. Selanjutnya eigentriple yang dikelompokkan ke dalam kelompok musiman adalah eigentriple 3, 4, 15, 16, 17, dan 18. Terakhir, sisa eigentriple yang tidak dikelompokkan ke dalam kelompok tren dan musiman merupakan kelompok noise.
Pada langkah diagonal averaging, masing-masing komponen dapat direkonstruksi menggunakan masing-masing eigentriple yang terkait. Pada kasus ini, komponen tren direkonstruksi oleh eigentriple 1 dan 2. Plot hasil dari komponen tren yang direkonstruksi adalah sebagai berikut:
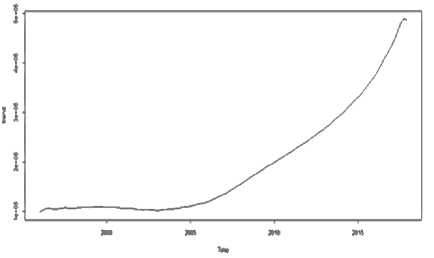
Gambar 5. Komponen tren yang direkonstruksi
Selanjutnya komponen musiman direkonstruksi oleh eigentriple 3, 4, 15, 16, 17, dan 18. Plot hasil dari komponen musiman yang direkonstruksi adalah sebagai berikut:
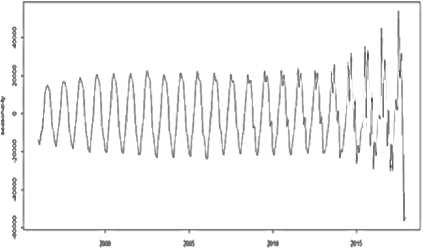
Gambar 6. Komponen musiman yang direkonstruksi
Selanjutnya plot hasil dari komponen noise yang direkonstruksi adalah sebagai berikut:
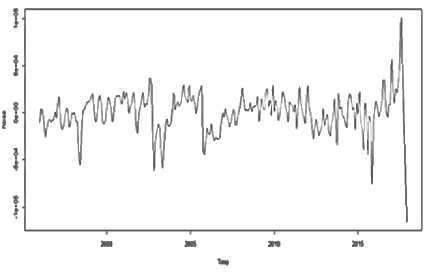
Gambar 7. Komponen noise yang direkonstruksi
Ketika komponen tren, musiman, dan noise berhasil dipisahkan, maka langkah selanjutnya adalah melakukan peramalan terhadap masing-masing komponen kecuali komponen noise. Jenis peramalan yang digunakan untuk meramalkan komponen tren dan musiman adalah recurrent singular spectrum analysis (RSSA). Nilai ramalan yang dihasilkan oleh model SSA dari masing-masing komponen terdiri dari nilai ramalan untuk data in-sample dan nilai ramalan untuk data out-sample. Secara matematis, model SSA yang digunakan untuk meramalkan komponen tren dapat ditulis sebagai berikut:
yl = 0,044yl-ι + 0,044 yl~2+․․․- 0,011yI-93 untuk i=265,266,…,276
Sedangkan model SSA yang digunakan untuk meramalkan komponen musiman dapat ditulis sebagai berikut:
Vi = 0,031yt-ι + 0,119Vi-2+⋯+0,005yf-93 untuk i=265,266,…276
Nilai ramalan untuk data out-sample secara keseluruhan diperoleh dari hasil penjumlahan nilai ramalan data out-sample dari komponen tren dan nilai ramalan data out-sample dari
komponen musiman. Secara matematis, model SSA yang digunakan untuk mendapatkan nilai ramalan data out-sample secara keseluruhan dapat ditulis sebagai berikut:
Vi = + Vi , untuk i=265,266,…,276
Setelah model SSA yang digunakan untuk melakukan peramalan sudah dibentuk, maka langkah selanjutnya adalah melakukan peramalan pada data out-sample berdasarkan model yang diperoleh. Akurasi hasil peramalan pada data out-sample diukur dengan nilai MAPE yang merupakan nilai rata-rata persentase kesalahan dari beberapa periode.
Tabel 2. Hasil Peramalan untuk Data Out-Sample dari Komponen Tren dan Komponen Musiman
|
Bulan |
Hasil ramalan |
Data aktual |
Persentase Kesalahan |
|
Januari |
427687 |
358065 |
0,194 |
|
Februari |
488157 |
452423 |
0,079 |
|
Maret |
485268 |
492678 |
0,015 |
|
April |
509024 |
516777 |
0,015 |
|
Mei |
533052 |
528512 |
0,009 |
|
Juni |
537607 |
544550 |
0,013 |
|
Juli |
568162 |
624366 |
0,090 |
|
Agustus |
529878 |
573766 |
0,076 |
|
September |
571158 |
555903 |
0,027 |
|
Oktober |
526414 |
517889 |
0,016 |
|
November |
524765 |
406725 |
0,290 |
|
Desember |
545155 |
498819 |
0,093 |
|
Total Persentase Kesalahan |
0,917 | ||
|
Nilai MAPE |
0,0764 | ||
Sumber: Data diolah, 2019
Menurut Zhang et al. (2015), nilai MAPE yang kurang dari 10% menunjukkan bahwa peramalan sangat akurat. Sedangkan nilai MAPE antara 10% hingga 20% menunjukkan bahwa peramalan baik. Berdasarkan Tabel 2, diperoleh nilai MAPE pada data out-sample sebesar 0,0764 atau 7,64%. Dengan demikian, dapat disimpulkan bahwa metode SSA dengan L=94 dapat meramalkan jumlah kunjungan wisatawan mancanegara ke Bali dengan sangat baik.
Berdasarkan hasil dan pembahasan yang telah dipaparkan pada bab sebelumnya, diperoleh model SSA yang digunakan untuk meramalkan komponen tren dua belas bulan ke depan yakni sebagai berikut:
y{ = 0,044y{-ι + 0,044yI-2+․․․- 0,011yt-∞ untuk i=265,266,…,276
Sedangkan model SSA yang digunakan untuk meramalkan komponen musiman dua belas bulan ke depan dapat ditulis sebagai berikut:
Vi = 0,031yf-ι + 0,119yt-2 +⋯+0,005Vi-n untuk i=265,266,…276
Model tersebut merupakan model SSA terbaik dengan nilai window length L=94 serta nilai MAPE sebesar 7,64%. Hal ini menunjukkan bahwa metode SSA dapat
meramalkan jumlah kunjungan wisatawan mancanegara ke Bali dengan sangat baik.
Adapun saran untuk penelitian selanjutnya yaitu diharapkan dapat menentukan nilai L dengan memilih nilai MAPE minimum tanpa proses pengelompokan.
DAFTAR PUSTAKA
Anisa, D. F. 2019. Sektor Pariwisata
Berpeluang Geser Sawit sebagai Penyumbang Devisa Terbesar. http://
www.beritasatu.com. Diakses 24 Maret 2019.
Assifa, F. 2019. Awal 2019, Jumlah Turis Mancanegara yang Kunjungi Bali Naik 31,6 Persen. https://regional.kompas.com.
Diakses 24 Maret 2019.
Golyandina, N., Nekrutkin, V., and Zhigljavsky, A. 2001. Analysis of Time Series Structure: SSA and Related Techniques. Florida: Chapman & Hall / CRC.
Hassani, H. 2007. Singular Spectrum Analysis: Methodology and Comparison. Journal of Data Science, 239-257.
Khaeri, H., Yulian, E., and Darmawan, G. 2017. Penerapan Metode Singular Spectrum Singular Analysis (SSA) pada Peramalan Jumlah Penumpang Kereta Api di Indonesia tahun 2017. Jurnal Euclid, Volume 5, No. 1, pp. 8-20.
Mardika, I. 2019. Bali Optimistis Sektor Pariwisata Bangkit di 2019.
https://www.beritasatu.com. Diakses 26 Maret 2019.
Zhang, T., Wang, K., and Zhang, X. 2015. Modeling and Analizing the Transmission Dynamics of HBV Epidemic in Xinjiang, China. Journal PLOS One, Volume 10, No. 9, pp. 1-14.
308
Discussion and feedback