KONTROL OPTIMAL PADA MODEL PENYEBARAN VIRUS KOMPUTER DENGAN KLASIFIKASI PENGAMANAN

E-Jurnal Matematika Vol. 8(4), November 2019, pp.253-258

DOI: https://doi.org/10.24843/MTK.2019.v08.i04.p261

ISSN: 2303-1751

KONTROL OPTIMAL PADA MODEL PENYEBARAN VIRUS KOMPUTER DENGAN KLASIFIKASI PENGAMANAN

Pangestuti Prima Darajat^1§, Tyas Husadaningsih²

¹Universitas Islam Raden Rahmat Malang [Email: pangestuti_prima@uniramalang.ac.id] ²Universitas Islam Raden Rahmat Malang [Email: tyas.husadaningsih@uniramalang.ac.id] ^§Corresponding Author

ABSTRACT

In this paper, a model of the spread of computer viruses with security classification and nonlinear infection rates is formulated. From the short analysis, is found that the model does not have a virus-free equilibrium point. This show that the virus will always exist in the system and increasingly that can not be avoided. Therefore, control strategy by installing antivirus on subpopulation susceptible low-security level and infective subpopulation aims to minimize the number of infective computers, and minimize the cost related to these strategies. Hence, an important tool, in this case is, optimal control theory. The system solved numerically by using Forward-Backward Sweep method in combination with the fourth-order Runge-Kutta method. Based on the simulation results, the combination of the two controls is effective in suppressing the spread of computer viruses. However, controlling by installing an antivirus on an infected computer has a great influence in suppressing the spread of the computer virus.

Keywords: Optimal Control, Mathematical Modeling, Computer Virus.

• 1.    PENDAHULUAN

Tingginya ketergantungan berbagai bidang pada kinerja komputer menjadikan virus komputer sebagai ancaman yang serius. Tidak jarang kerusakan akibat virus ini dapat menyebabkan kerugian finansial yang besar. Sementara itu, software antivirus sebagai alat untuk mengatasi virus komputer memiliki kemampuan terbatas dan perkembangannya tertinggal oleh virus-virus berbahaya baru yang tercipta. Para peneliti telah mengembangkan berbagai model matematika untuk menggambarkan dinamika penyebaran virus komputer demi mendapatkan model yang sesuai dengan realita. (Yang, 2012-2014), (Zhu, 2013), (Gan, 2017), (Zhu, 2017), (Darajat, 2016).

Penelitian ini bertujuan untuk mengkontruksi model matematika yang lebih realistis tentang penyebaran virus komputer sekaligus mendapakan strategi yang efektif dalam penekan penyebaran virus komputer pada masa yang akan datang. Pada teori matematika terdapat dua pendekatan penting untuk mengontrol penyebaran virus, yaitu analisis kualitatif (analisis dinamik) dan teori kontrol optimal. Pada analisis dinamik kondisi

penyebaran pada masa yang akan datang dapat diprediksi. Sementara itu, dengan teori kontrol optimal didefinisikan strategi-strategi untuk menekan penyebaran penyakit sehingga kemudian diperoleh strategi terbaik dalam menekan penyebaran penyakit (Darajat, 2016).

Pada penelitian ini dikonstruksi suatu model yang memodifikasi model penyebaran virus komputer dengan klasifikasi pengamanan oleh Zhu dan Cen pada tahun 2017 serta menggunakan laju infeksi nonlinear yang lebih realistis yang digunakan pada model Gan tahun 2017. Komputer bebas virus diklasifikasikan menjadi dua, yaitu Susceptible low security level (S _l) sebagai subpopulasi komputer bebas virus yang memiliki pengamanan rendah dan Susceptible high security (Sf_l) sebagai subpopulasi komputer bebas virus yang memiliki pengamanan tinggi. Sementara itu, subpopulasi komputer terinfeksi (Infected Computers) dinotasikan dengan I. Beberapa asumsi dikenakan pada model sedemikian sehingga dapat sesuai dengan kondisi sebenarnya yaitu,

• (i) . Komputer 5; dan Sfi terkoneksi dengan internet dengan laju sebesar bi dan bh .

• (ii) . Masing-masing komputer akan terputus koneksinya dengan internet dengan laju sebesar μ.

• (iii) . Didefinisikan parameter a sebagai laju komputer susceptible high security ( ^h ) yang menjadi komputer susceptible low security (Si ) karena melemahnya program antivirus pada komputer tersebut.

• (iv) . Akibat interaksi dengan komputer terinfeksi I , Komputer Si dan komputer S ^ akan terinfeksi dengan laju sebesar βιl dan β_hI⁄f(I) dengan f(I)=1+I.

• (v) . Diasumsikan bahwa pengguna melakukan pembersihan menggunakan program antivirus pada komputer yang terinfeksi, dengan demikian komputer terinfeksi I akan bersih dari virus dan berubah menjadi komputer Si dan S^ dengan laju masing-masing sebesar γ_iι dan γ_hI.

• (vi) . Akibat penggunaaan perangkat remofable storage, komputer $1 akan terinfeksi dengan laju sebesar δ.

Asumsi-asumsi yang telah dibangun di atas selanjutnya disajikan dalam diagram kompartmen pada Gambar 1.

Gambar 1. Diagram Komartment Model

Model penyebaran virus komputer dengan klasifikasi pengamanan dan laju infeksi nonlinear adalah sebagai berikut,

^̇ =  + γβ - ββSι + CtSh - SSi

^- μs_t

,      , r                                               „

5^̇ =   + YhI - l^{Sh -} Ct Sj₁ ^- μs_h

. _n       , βhl _n , _{r 1}

İ=     + ₁s_h ^- YiI ^- YhI + SSi

^- ^i

(1)

Diketahui bahwa sistem persamaan (1) tidak memiliki titik kesetimbangan bebas virus. Hal ini dapat diinterpretasi bahwa, pada masa

yang akan datang jumlah komputer terinfeksi semakin besar (Boyce, 2009). Simulasi sistem (1) dengan parameter merujuk pada Zhu tahun 2017 yang disajikan pada Tabel 1. adalah sebagai berikut,

Tabel 1. Nilai Parameter

bι	0,0012
bh	0,0018
βl	0,05
βh	0,05
Yi	0,146
Yh	0,003
a	0,005
δ	0,003
μ	0,003

Hasil Simulasi model dapat dilihat pada Gambar 2. Ditunjukkan bahwa jumlah komputer terinfeksi meningkat dari waktu-ke waktu. Sementara itu jumlah komputer ^l maupun ^h semakin menurun. Populasi awal S^o=10, ^h =15, I=5 untuk T=25 populasi akhir yang diperoleh adalah ^^0 =3, ^h =4,I=20.

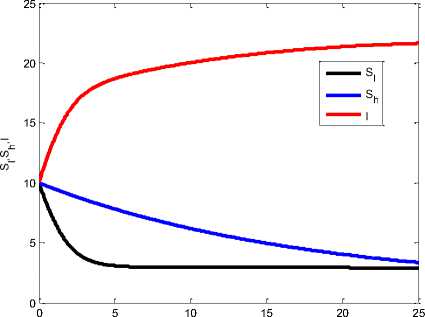
Waktu

Gambar 2. Simulasi Model Penyebaran Virus Komputer dengan Klasifikasi Pengamanan

Oleh karenanya diusulkan beberapa strategi pengontrolan untuk menekan jumlah komputer terinfeksi. Strategi pengontrolan dengan menginstal antivirus pada komputer $i dinotasikan dengan U₁ (t). Pengontrolan ini ditujukan untuk menambah perlindungan komputer ^l ketika berinteraksi dengan komputer terinfeksi maupun dengan perangkat removable storage. Strategi pengontrolan dengan menginstal antivirus pada komputer terinfeksi (I) dinotasikan dengan u₂ (t). Pengontrolan ini bertujuan untuk mengurangi jumlah penginfeksi. Dalam hal ini u₁ (t) dan u₂ (t) menyatakan nilai

yang dinormalisasi sedemikian hingga batas kontrol diberikan sebagai berikut,

U_a d = {u (O)₁U₂V ^ L²0)≤ u ₁(t) ≤l,O≤U2(t)≤l,t   (2)

∈ [0,T].

Berdasarkan keterbatasan kemampuan suatu antivirus, pada model kontrol diasumsikan bahwa, laju komputer terinfeksi I yang menjadi komputer S_fl pada waktu t adalah sebesar ηu₂ ( t) dan laju komputer terinfeksi yang menjadi komputer S₁ adalah sebesar (1 —

) ( ) dengan ∈ [0,1]. Model penyebaran Virus komputer dengan penambahan kontrol adalah sebagai berkut,

^S i = b i + YiI ^{— (}1 ^— u )((βιl S i + ^sS ) + sS— — [lS i + T] 'U 2 I

$h - b — ^{+ γ}f^{1 —} 1₊ j^S— ^{— sS}— ^— ^^S— + (1 — )

I -(l — UiWiISi + SSO+^S— ^{— γ}ι^{1 —} Y—^{1 —} μ^{1 —} u₂¹

• 2.    METODE PENELITIAN

Pada masalah kontrol optimal, variabel yang termuat pada sistem persamaan diferensial disebut sebagai variabel-variabel state. Variabel-variabel state ini akan dikendalikan dengan diberi perlakuan berupa fungsi kontrol yang sesuai. Fungsi kontrol yang dimaksud dapat mempengaruhi perilaku state sedemikian sehingga dapat mengoptimalkan fungsional objektif yang berbentuk integral fungsi yang bergantung pada variabel state dan variabel kontrol. Teknik utama untuk menyelesaikan masalah kontrol optimal adalah menentukan syarat perlu yang memenuhi kondisi optimal dan state. Syarat perlu yang diusulkan oleh Pontryagin pada tahun 1950 disebut sebagai fungsi adjoint. Fungsi adjoint digunakan untuk menambahkan persamaan diferensial pada fungsional objektif . Fungsi adjoint secara sederhana dapat dibangkitkan oleh fungsi Hamilton (Lenhart, 2015).

Kondisi optimal sistem ditentukan menggunakan prinsip Pontryagin dan selanjutnya diselesaikan secara numerik menggunakan metode Sweep Maju-Mundur dikombinasikan dengan metode Rungge-Kutta orde 4. Dibentuk fungsional objektif pada periode waktu [0, ] yang mendeskripsikan

tujuan pengontrolan yaitu meminimumkan jumlah komputer terinfeksi dan meminimumkan biaya total untuk menginstal antivirus pada komputer. Didefinisikan konstanta bobot seperti pada Tabel 2.

Tabel 2. Konstanta Bobot Fungsional Objektif.

Notasi	Keterangan
41	konstanta bobot yang berkaitan dengan jumlah komputer terinfeksi
A2	konstanta bobot yang berkaitan dengan biaya pengontrolan u 1( t).
A2	konstanta bobot yang berkaitan dengan biaya pengontrolan u 2 (t).

Dengan demikian fungsional objektif yang akan diminimumkan adalah

(3)

J (U1,U2 ))- f Jo

[A i I^+A 2 U²V

(4)

+       ( )]   ,

dengan kendala persamaan (2).

Variabel-variabel state pada masalah ini adalah ( ), ( ), dan ( ). Didefinisikan variabel-variabel adjoint yang bersesuaian untuk variabel-variabel state adalah ( ), ( ), dan σ₃ ( t). Selanjutnya, dapat dibentuk fungsi Hamilton sebagai berikut

H^(Sl, ^S—, I > ^U1 ^{, u}2 ^,11> @2^, @3 V —

A i I (t') + A 2 u(V + A ₃ u(V 3

+ ∑σ_i(tVι(Sι,Sf,I,Uι,U2), i=i

(5)

dengan kondisi batas transversal adalah

σ_i (T) — 0, i = 1,2.            (6)

• 3.    HASIL DAN PEMBAHASAN

  • 3.1    Penyelesaian Masalah Kontrol Optimal

Penyelesaian masalah kontrol optimal akan disajkan pada teorema berikut,

Teorema 1. Pada masalah kontrol optimal persamaan (4) dengan kendala sistem persamaan (3), terdapat kontrol optimal u 2(t), dan u ₂( t) dan solusi state optimal S2(t),S2(t),Γ(t) sedemikian sehinggan nilai J(u2,u2) minimum. Selain itu, terdapat variabel adjoint     ,  , dan     yang memenuhi

persamaan berikut,

dσ₁ dt

∂σ₂ dt ^:

∂σ₃ dt

^-σ)(^-(^{1 - u})KβιJ + 5) ^- μ)

• ^{-    σ}3((^{1 - u}))(^βι^{1 + 5))}

M ( ^βhl       ∖

^-σ)W ^{- σ}2 (^-γ∑^7- ^{α -} ^) ( ^βhl ∖

• ^{-    σ}≡ (in)

-A) ^- θ((γ- ^{- (1 -} U))^β_iSι

Kondisi optimal diperoleh ketika fungsi Hamilton memenuhi kondisi stasioner, yaitu

_rdH     , , _

0-— , vuμ-i,2.

du 2         *

(9)

+ ηu2)

Berdasarkan kondisi stasioner pada persamaan (7), maka dapat ditentukan kondisi u 2 (t), u₂(t), dan u₃( t) agar diperoleh sistem optimal adalah sebagai berikut,

^σ (^γ        .;_:-

+ ⁽1 →∕>2 )

(7)

- (i -  )

⁺ (1 + I )^{2 Sh}

^- μ^-u 2 I

^-γι^-γh

dengan kondisi transversal pada persamaan (6).

0-2    +  (   +  )

- σ₃(β√Sι + 5Sι)        (10)

0 — 2A ₃ u₂ + σ₁ ηl + σ₂(1 — η)/ — σ₃ 1

Berdasarkan persamaan (9) dan (10), maka perhitungan nilai ² ( ),  ² ( ), dan ² ( ) dapat

dilakukan dengan persamaan sebagai berikut,

²( )

( σ3-σ) )(βιlSι + 5Sι)

^,           2A₂

— m in {max (

)'¹

(11)

Bukti. Sistem persamaan adjoint dan kondisi tranfersal ditentukan melalui fungsi Hamilton pada persamaan (4). Nilai negatif turunan fungsi Hamilton untuk masing-masing variabel state diperoleh yaitu memenuhi,

dσ₁ dt

∂σ₂ dt

∂σ₃ dt

^- -τy - ^-σ)(^-(^{1 - u}))(^βι¹ + 5)

^- ^)

-σ₃((1-U))(β√ + δ))

∂H

^-^τr^ ^{- -σ})(^α)

^^h

( ^βhl \

• ^{- σ}2[^-i+1^-a-μ)

∕ ^βhl \

• ^{-    σ}≡       /^!

∂H .

^-dT^{--A) - c}^(^γι

• -    (i -  )    +    )

L. ^βh c

• ^-σ2V^h-l1+iy^Sh

+ ⁽i - η >2)

^{- σ}3 ^{((1 - U})^)βl^Sl

1 ^βh c

⁺ (i+∕)2^s^^-γι-γ^

^- μ^-u2 I

²( )

■ f Λ (^σ3^-σ)η^-σ2(^1-η))Λ — m in {max (0,--------—---------I,

Misalkan ²,  ² , ² adalah kondisi state optimal,

dan Oi, σ₂, σ₃ adalah kondisi variabel adjoint yang bersesuaian. Kondisi optimal diperoleh dengan menyelesaikan sistem yang telah disubstitusikan nilai ² ( ) dan ² ( ) sebagai berikut

dS ²

-f)(S t, S²_h, 1², u 2,u2),

(8)

^^l - f2(St,St,1*,ut,ut)

di²

— -f3(S²,S2,1²,ut,ut)

d σ²

~τr ^{- -σ})^{(—(1 - u}))(^βι^{1 + 5})^-ri dt

-  ((1 -  )(

+ 5))

d σ2 _           ∕ β√

_^--σi(_σ)^-σ2(-i_^-_σ^-_μ

(12)

_-

( ^βhl \

^σ3    ■ ^J

∂σ ^∗ ∂t

^-Ai ^- ¾⁽Yi-(1-u_r ⁾βι⅛ι

+ ηu₂ )

( β_h

^- σ₂ ^{(  -}(1+I)

+(1-V)^2 )

dihindari. Sementara itu, jika digunakan pengontrolan U₂ saja jumlah komputer terinfeksi berkurang dengan lebih cepat sehingga kerugian dan kerusakan pada komputer Sf_l maupun $1 dapat dihindari.

_-

((1-U₁ )βι⅛ι

+

(1+I)2^Sh ^- Yi

μ^-  )

_-

Yh

• 3.2    Simulasi Penyelesaian Secara Numerik

Sistem persamaan optimal (12) akan diselesaikan secara numerik menggunakan metode sweep maju mundur yang dikombinasikan dengan metode Rungge-Kutta orde 4 (Lenhart, 2015). Parameter yang digunakan pada tabel 1 ditambahkan nila ^rI = 0,6. Simulasi dilakukan untuk membandingkan pengaruh pengontrolan Ui , u₂ , dan keduanya terhadap sistem. .Nilai awal yang dihunakan adalah ( $1 , Sf_l ,I) =(10,10,10).

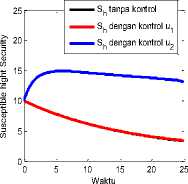
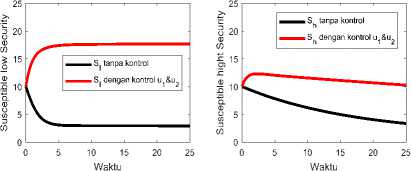
Simulasi masing-masing upaya pengontrolan U₁ dan u₂ disajikan pada Gambar 3. Solusi numerik sistem tanpa kontrol (garis hitam) menunjukkan Jumlah komputer Si dan Sf_l semakin berkurang sementara jumlah komputer terinfeksi I semakin bertambah. Solusi sistem tanpa kontrol konvergen ke nilai (S ∗, S ∗, I∗)= (2.9, 3.3, 21.6). Pada saat diberikan strategi pengontrolan dengan menginstal antivirus pada komputer Si yaitu U₁ saja (Garis Merah) jumlah komputer $1 meningkat secara signifikan akan tetapi jumlah komputer Sf_l tetap turun seiring bertambahnya jumlah komputer terinfeksi (I). Hasil simulasi sistem dengan kontrol u₁ konvergen ke nilai (S ∗_, S ∗_, I^∗)=(22.0,3.4 , 2.5).

Ketika sistem diberikan strategi pengontrolan dengan menginstal antivirus pada komputer terinfeksi I (1^2) saja sistem konvergen ke titik (S ∗_, S ∗_, I^∗)=(12.5,13.1, 2.3). Jumlah komputer $i dan Sf_l bertambah meskipun kurang signifikan semetara komputer terinfeksi berkurang dengan cepat. Baik pengontrolan U₁ maupun U₂ dapat mengurangi jumlah komputer terinfeksi, namun jika digunakan pengontrolan U₁ saja kerusakan dan kerugian pada komputer S^ tidak dapat

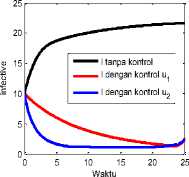
Gambar 3. Simulasi pengaruh masing-masing pengontrolan U₁ (Garis Merah) dan 1^2 Garis Biru.

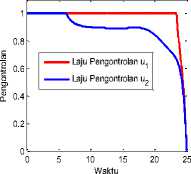
Simulasi selanjutnya digunakan kedua strategi kontrol yaitu U₁ dan U₂ . Solusi numerik sistem (10) dengan kedua strategi kontrol konvergen ke titik (S ∗_, S ∗_, I^∗) = (17.6, 10.3, 0) seperti disajikan pada Gambar 4. Solusi sistem menggambarkan kedua pengontrolan dilakukan dengan maksimum (U₁ = =1) sehingga jumlah komputer terinfeksi cepat menuju nilai 0. Akibat dari kedua pengontrolan tersebut, jumlah komputer Si meningkat secara signifikan, sementara jumlah komputer Sf_l cenderung tetap.

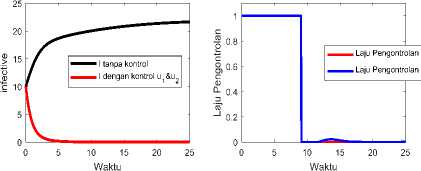
Gambar 4. Hasil simulasi pengaruh pengontrolan U₁ dan 112 .

Berdasarkan hasil simulasi pada Gambar 3. Gambar 4. dapat diketahui bahwa pengontrolan dengan menginstal antivirus pada komputer I saja lebih efektif dalam menekan penyebaran virus komputer dibandingkan pengontrolan dengan menginstal antivirus pada komputer Si saja. Dengan kata lain, menginstal antivirus pada komputer terinfeksi dapat meminimalisir subjek penginveksi secara langsung sehingga penyebaran virus komputer dapat diatasi. Namun demikian, kombinasi kedua pengontrolan yakni penginstalan antivirus pada komputer Si sebagai tindakan preventif pencegahan penyebaran virus komputer dan penginstalan antivirus pada komputer I untuk mengurangi subjek penginveksi merupakan tindakan yang paling efektif untuk mengatasi penyebaran virus komputer.

• 4.    KESIMPULAN

Berdasarkan hasil penelitian dapat disimpulkan bahwa, strategi pengontrolan penyebaran virus komputer yang efektif adalah dengan menginstal antivirus pada subpopulasi komputer dengan pengamanan lemah juga pada subpopulasi komputer terinfeksi. Pengontrolan pada subpopulasi komputer dengan pengamanan lemah bertujuan untuk melindung subpopulasi tersebut ketika berinteraksi dengan komputer terinfeksi maupun perangkat removable storage. Pengontrolan pada subpopulasi komputer terinfeksi bertujuan meminimalisir penginfeksi. Pengontrolan pada komputer terinveksi ini memiliki pengaruh yang signifikan dalam menekan penyebaran virus komputer.

• 5.    SARAN

Pada penelitian selanjutnya dapat dikontruksi model penyebaran virus komputer lain yang lebih realistis dengan penambahan asumsi-asumsi lain. Strategi pengontrolan juga dapat diaplikasikan pada model penyebaran virus komputer lain karena telah terbukti efektif.

DAFTAR PUSTAKA

Boyce, W.E dan R.C. DiPrima. 2009. Elementary Differential Equations and Boundary Value Problems Eight Edition. USA: John Willey and Sons, Inc.

Chen, L., Hattaf, K., dan Sun, J. 2015. Optimal control of a Delayed SLBS computer virus model. Physica A. 427 : 244-250.

Darajat, P. P., Agus S., Agus W. 2016. Optimal Control On The Spread Of Slbs Computer Virus Model. International journal of pure and Applied Mathematics. 107:3.

Gan, C., Maobin Y., Zufan Z., dan Wanping L. 2017. Global Dynamics and Optimal Control of a Viral Infection Model with Generic Nonlinear Infection Rate. Discrete Dynamics in Nature and Society. 7571017.

Lenhart, S., dan Workman, J. T. 2015. Optimal Control Apllied to Biological Models. Taylor & Francis Group. New York.

Yang, L. X., dan Yang, X. 2014. A New Epidemic Model of Computer Viruses. Commun Nonlinear Sci Numer Simulat. 19: 1935-1944.

Yang, L. X., Yang, X., Zhu, Q., dan Wen, L. 2013. A Computer Virus Model With Graded Cure Rates. Commun Nonlinear Sci Numer Simulat. 19: 1935-1944.

Yang, X., dan Yang, L. X. 2012. Towards the epidemiological Modeling of Computer Virus. Discrete Dynamics in Nature and Society. 25967.

Zhu, Q., dan Chen Cen. 2017. A Novel Computer Virus Propagation Model under Security Classification. Discrete Dynamics in Nature and Society. 8609082.

258