E-Jurnal Matematika Vol. 8(4), November 2019, pp.259-263

DOI: https://doi.org/10.24843/MTK.2019.v08.i04.p262

ISSN: 2303-1751

PEMODELAN NILAI KURS TERHADAP HARGA SAHAM PADA DATA LONGITUDINAL MENGGUNAKAN REGRESI NONPARAMETRIK SPLINE TRUNCATED

Milatus Sholikha1§, Made Susilawati 2, I Gusti Ayu Made Srinadi 3

1Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: milatussholikha@gmail.com] 2Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: mdsusilawati@unud.ac.id] 3Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: srinadi@unud.ac.id]

§Corresponding Author

ABSTRACT

The purpose of this study was to obtain the models between currency value and stocks in longitudinal data. The models were obtained by using nonparametric truncated spline regression. The data consisted of stocks from three companies namely PT. Mandom Indonesia, PT. Unilever Indonesia and PT. Akasha Wira Internasional and currency value of AUD to IDR. The data were splitted into two sub samples which were “in sample” data from January 2013-December 2017 that were used to generate the models and “out sample” data from January 2016-December 2018 to validate the models, MAPE was used as measurement in validation. This resulted in three distinctive models which were model with 3nd order and 3 knots for PT. Mandom Indonesia and PT. Unilever Indonesia, model with 2nd order and 4 knots for PT. Akasha Wira Internasional stock, all with there own respective knot points and MAPE value of 9.62%, 15.61% and 48.8% sub sequently.

Keywords: stocks, longitudinal data, nonparametric truncated spline regression, GCV

  • 1.    PENDAHULUAN

Perkembangan ekonomi pada suatu negara menjadi salah satu perhatian pemerintah untuk membawa bangsanya kepada kehidupan yang lebih baik, perkembangan ekonomi dapat terlihat dari indikator pasar modal pada negara tersebut. Menurut Muklis (2016) keberadaan pasar modal di Indonesia merupakan salah satu faktor penting dalam pembangunan perekono-mian nasional, terbukti telah banyak industri dan perusahaan yang menggunakan institusi ini sebagai media untuk menyerap investasi dan memperkuat posisi keuangannya. Salah satu investasi yang ditawarkan investor di pasar modal adalah saham. Saham dapat didefini-sikan sebagai tanda kepemilikan seseorang atau badan dalam suatu perusahaan maupun perseroan terbatas.

Faktor-faktor yang memengaruhi pergerakan harga saham, yaitu faktor internal dan faktor eksternal. Faktor internal merupakan faktor yang berkaitan langsung dengan kinerja atau kondisi suatu perusahaan yang dilihat dari data-data laporan keuangan selama perusahaan melakukan kegiatan operasinya. Faktor eksternal

merupakan faktor yang tidak berkaitan langsung dengan kondisi perusahaan, seperti tingkat suku bunga, tingkat inflasi, kurs valuta asing dan sebagainya (Agustina dan Sumartio, 2014).Data harga saham dari beberapa perusa-haan yang diamati dalam kurun waktu tertentu termasuk data longitudinal atau sering disebut dengan data panel. Data longitudinal merupa-kan data yang dihimpun dari suatu pengama-tan atau pengukuran atas sejumlah subjek yang dilakukan berulang dari waktu ke waktu.

Tujuan penelitian ini adalah memodelkan nilai kurs terhadap saham pada data longitudinal dengan menggunakan metode regresi nonparametrik spline truncated. Secara umum data longitudinal dapat ditulis sebagai berikut:

  • ( Yij ,Xlj} ; i = 1,^.,n,j = 1,^.,m

n menyatakan banyaknya subjek dan m menyatakan banyak amatan tiap subjek, dengan Yi j menyatakan variabel respon untuk subjek ke- i dan waktu ke-j dan Xij menyatakan variabel prediktor untuk subjek ke- dan waktu ke- .

Data harga saham cenderung fluktuatif dan tidak berdistribusi normal sehingga data dapat

diestimasi menggunakan pendekatan regresi nonparametrik.

Secara umum model regresi nonparametrik sebagai berikut (Eubank, 1999):


k

K =∑

tnm ∕ uPn-^nm

P=Q


K

+∑Prr (Xnm


-


k

^rn )+ ^nm


(5)


Dengan demikian persamaan 5 dapat disajikan


Yl =(Xt)+εl,i=1,2,…․,n          (1)


dalam bentuk matriks seperti pada persamaan 6 berikut:


Yi menyatakan variabel respon pada subyek ke- i,f( xi ) menyatakan variabel prediktor yang tidak diketahui kurva atau polanya, xi menyatakan variabel prediktor pada subyek kei , dan Ei merupakan error pengukuran pada subjek ke-i. Model regresi nonparametrik untuk data longitudinal adalah sebagai berikut (Suparti et al, 2017):


N=   +ε


(6)


dimana


Yij =(xij)+εij ,i=1,2,…․,


j = 1,2,


․,


n; m


(2)


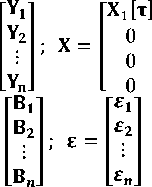
0

X2 [τ]

0

0


00

0    0  ];

0 Xn [τ]


Yij menyatakan variabel respon pada subyek kei waktu ke- j,f( xij ) menyatakan variabel prediktor yang tidak diketahui kurva atau polanya, xij menyatakan variabel prediktor pada subyek ke- i waktu ke- j , dan εij merupakan error pengukuran pada subjek ke-i waktu ke-j.

Salah satu estimator pada regresi nonpara-metrik adalah spline. Pendekatan regresi nonparametrik menggunakan metode spline cenderung mencari sendiri estimasi data dari pola yang terbentuk (Budiantara,  2011).

Beberapa hal yang perlu diperhatikan dalam membentuk regresi spline adalah menentukan orde model, banyaknya titik knot, serta lokasi knot tersebut (Toruan, 2018). Secara umum persamaan fungsi regresi nonparametrik spline truncated berorde k dengan titik knot = { ^l , T2,…, ^K }    misalkan terdapat data

longitudinal dengan i=1,2,…․,n;=

1,2,…․,m sebagai berikut (Suparti et al, 2017): kK

f(Ztt)=∑Vij +∑βri (Itl - τrι )+(3)

P=Or=l


Dengan menggunakan metode Ordinary Least

Square (OLS), diperoleh estimator untuk


parameter β sebagai berikut:


̂=(XtX) -1xty          (7)


Fungsi estimator dari f(X) untuk regresi nonparametrik spline dengan titik knot K= { ^"1 , T2,…,TK} sebagai berikut:


̂ 'i (X)=%k ̂k=   (XkXk)~1Xκγ    (8)

Sehingga dapat ditulis:

̂K=   (XkXk)~1Xκγ =         (9)

̂ K =( ̂ 1 ,…, ̂ n )T , dengan ̂ = ̂ i (X) dan


^K =   (XkXk) 1Xk         (10)


k, ®o , OCγ , ¾ ,…, ^k , βl , β2,…,βκ


adalah


parameter-parameter yang tidak diketahui, dan


{Tri ; Tr1 < Tr2 <⋯ < Trκ }


merupakan


Pemilihan titik knot optimal sangat penting dalam regresi nonparametrik, karena estimator spline terbaik diperoleh dengan menggunakan titik knot optimal. Titik knot merupakan titik perpaduan bersama dimana terdapat perubahan pola perilaku fungsi atau kurva. Titik knot optimal dapat ditentukan dengan menggunakan nilai Generalized Cross Validation (GCV) (Litawati dan Budiantara, 2013).

Pemilihan menggunakan nilai GCV dapat didefinisikan sebagai berikut:


himpunan titik knot ke-r dari subjek ke-i , serta ( xij - τis )+ merupakan fungsi truncated yang dapat dijabarkan sebagai berikut:


GCV(K)=


m 1∑ Th [Xij - ̂G]      (11)


{1-tr (Ak)⁄m}2


(Xij - τis )  ={( ⅛


-


't); xIj ≥ Tri ; Xij < Tn


(4)


GCV(K) merupakan vektor yang memuat nilai GCV dari K yang merupakan titik-titik knot, m


Sehingga persamaan regresi nonparametrik untuk data longitudinal dapat disajikan sebagai berikut:


adalah banyaknya pengamatan, XiJ menyatakan variabel respon untuk subjek ke-i dan waktu ke-j, γ^κ = (XkXk) 1Xk .

Salah satu cara untuk mengetahui ketepatan peramalan sebuah model dapat menggunakan nilai Mean Absolute Percentage Error (MAPE).


Nilai MAPE dapat memberikan petunjuk tentang seberapa besar rata-rata kesalahan absolut peramalan. Rumus untuk menghitung nilai MAPE sebagai berikut:

∑It1 ∑M |(2≡ ̂ ^) ×100%|

MAPE =           Jlj              (12)

∑i=i ^i

Jika nilai MAPE yang diperoleh semakin kecil maka semakin akurat peramalan sebuah model. Interpretasi dari nilai MAPE yang dihasilkan (Chen et al, 2007):

  • 1.    MAPE < 10%         :    peramalan

tersebut sangat akurat

  • 2. 10%≤MAPE<20%   :   peramalan

tersebut baik

  • 3.    20%≤MAPE<50%   :   peramalan

tersebut cukup

  • 4.    MAPE ≥ 50%         :    peramalan

tersebut tidak akurat

  • 2.    METODE PENELITIAN

  • A.    Jenis dan Sumber Data

Data yang digunakan dalam penelitian ini adalah data sekunder yang diperoleh dari website resmi Bank Indonesia untuk data nilai kurs tengah AUD terhadap rupiah dari Januari 2013–Desember 2017, sedangkan data harga saham bulanan periode Januari 2013–Desember 2017 diperoleh dari website yahoo finance. Data out sample yang digunakan dalam penelitian ini adalah data saham bulanan periode Januari 2016–Desember 2018.

  • B.    Teknik Analisis Data

Tahapan analisis dalam penelitian ini adalah:  (1) Membuat scatterplot untuk

variabel respon dengan variabel prediktor pada masing-masing perusahaan. (2) Menentukan titik knot optimal menggunakan nilai Generalized Cross Validation (GCV) minimum pada setiap perusahaan. (3) Membentuk model spline terbaik berdasarkan titik knot optimal pada setiap perusahaan.

  • (4)    Menghitung akurasi dugaan model terbaik menggunakan nilai MAPE pada data out sample.

  • 3.    HASIL DAN PEMBAHASAN

  • A.    Scatterplot Pada Setiap Perusahaan

Membuat scatterplot bertujuan untuk mengetahui apakah kurva regresi yang

diidentifikasikan melalui plot-plot membentuk suatu pola tertentu atau tidak.

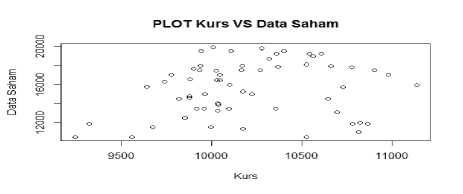
Gambar 1. Scatterplot PT. Mandom Indonesia (Sumber: Data diolah)

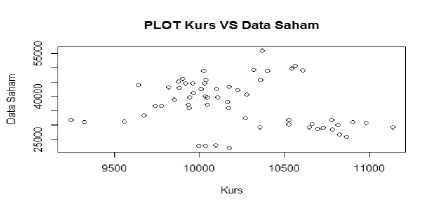
Gambar 2. Scatterplot PT. Unilever Indonesia (Sumber: Data diolah)

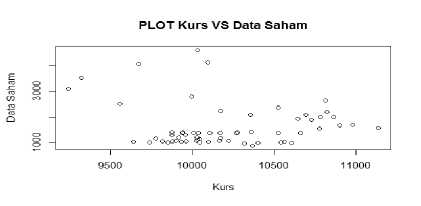
Gambar 3. Scatterplot PT. Akasha Wira

Internasional (Sumber: Data diolah)

Dari gambar scatterplot pada masing-masing perusahaan, dapat dilihat bahwa data memiliki pola yang berubah-ubah pada setiap rentang nilai amatan, sehingga pada penelitian ini data nilai kurs terhadap harga saham akan diestimasi menggunakan pen-dekatan regresi nonparametrik.

  • B.    Pemilihan Titik Knot Pada Setiap

    Perusahaan

Pemilihan titik knot optimal sangat penting dalam menentukan model regresi nonpara-metrik terbaik. Titik knot merupakan titik perpaduan bersama dimana terdapat perubahan pola perilaku fungsi atau kurva. Titik knot optimal dapat diperoleh dengan mencari nilai GCV minimum.

Pemilihan nilai GCV minimum dengan melakukan percobaan pada orde terendah yaitu

orde 2 (model linier) dan jumlah titik knot 1, lalu dilanjutkan dengan menambahkan orde dan titik knot sampai menghasilkan nilai GCV minimum, jika penambahan orde dan titik knot menghasilkan nilai GCV yang lebih besar maka penambahan orde dan titik knot tidak optimal.

Nilai GCV minimum pada setiap perusahaan dapat dilihat pada Tabel 1.

Tabel 1․ Nilai GCV Minimum

Perusahaan

Orde

Jumlah Knot

Titik Knot

Nilai GCV

PT.Mandom Indonesia Tbk (TCID)

3

3

10099,89;

10316,38;

10606,31

7111340

PT.Unilever Indonesia Tbk (UNVR)

3

3

10099,8 ;

10316,38;

10606,31

55996260

PT. Akasha Wira Internasional Tbk (ADES)

2

4

9879,97;

10006,65;

10099,89;

10316,38

620822

  • C.    Menentukan Model Spline Truncated Terbaik Pada Setiap Perusahaan

Model untuk data longitudinal terbaik menggunakan regresi nonparametrik spline truncated diperoleh dengan mencari nilai GCV minimum, setelah diperoleh nilai GCV minimum maka dapat ditentukan estimasi parameter pada setiap perusahaan, dapat dilihat pada Tabel 2.

Tabel 2․ Estimasi Parameter

Perusahaan

Parameter

Estimasi Parameter

PT. Mandom

aIO

-615668,6

Indonesia Tbk

«11

123,6

(TCID)

«12

-0,006

P13

0,028

P14

-0,073

PlS

0,086

PT. Unilever

a20

-3409635

Indonesia Tbk

a21

703,22

(UNVR)

a22

-0,035

P 23

0,212

P 24

0,4

P 25

0,341

PT. Akasha

a30

39319,34

Wira

a31

-3,87

International

P 32

8,75

Tbk (ADES)

P 33

-3,23

P 34

-4,48

P 35

3,96

Dari estimasi yang diperoleh pada Tabel 2, maka dapat dibentuk persamaan model regresi

nonparametrik spline truncated untuk data longitudinal pada masing-masing perusahaan sebagai berikut:

  • a)    Perusahaan 1 (TCID):

ĵ (X)=

⎧-615668,6 + 123,6x - 0,006X2    ;X < 10099,89

  • ⎪2240549,18 - 441,99X + 0,022X2 ; 10099,89 ≤ X < 10316,38

⎨-5528672,65 + 1064,18X - 0,051X2; 10316,38 ≤ X < 10606,31

  • ⎩⎪ 4145795,16 - 760,1X + 0,035X2    ;X ≥ 10606,31

  • b)    Perusahaan 2 (UNVR):

î ( X )=

⎧ -3409635 + 703,22X - 0,035X2 ;X < 10099,89

  • ⎪ 18216013,39 - 3479,13X + 0,177X2; 10099,89 ≤ X < 10316,38

⎨-24355064,59 + 4673,97X - 0,22X2; 10316,38 ≤ X < 10606,31

  • ⎩⎪ 14005325,24 - 2559,53X + 0,012X2 ;X ≥ 10606,31

  • c)    Perusahaan 3 (ADES):

ĵ (X)=

39319,34 - 3,87X               ;X < 9879,97

⎪⎧ -47130,39 - 4,88X             ; 9879,97 ≤ X < 10006,65

-14808,91 + 1,65X             ; 10006,65 ≤ X < 10099,89

30438,59 - 2,83X               ; 10099,89 ≤ X < 10316,38

⎩-10414,27 + 1,13X             ;X ≥ 10316,38

  • D.    Menentukan Nilai MAPE

Nilai MAPE dapat digunakan untuk mengetahui ketepatan sebuah model yang diperoleh.

Diperoleh nilai MAPE untuk model pada setiap perusahaan dengan menggunakan persamaan 12 sebagai berikut:

  • 1.    MAPE untuk ^l (PT. Mandom Indonesia) sebesar 9,62%

  • 2.    MAPE untuk ^2 (PT. Unilever Indonesia) sebesar 15,61%

  • 3.    MAPE untuk Y3 (PT. Akasha Wira Internasional) sebesar 48,8%

  • 4.    KESIMPULAN DAN SARAN

Berdasarkan pembahasan tersebut, dapat disimpulkan bahwa pada perusahaan Mandom Indonesia nilai GCV minimum sebesar 7111340 terletak pada orde 3 dengan 3 jumlah knot yaitu pada titik knot 10099,89 ; 10316,38 ; 10606,31. Pada perusahaan Unilever Indonesia nilai GCV minimum sebesar 55996260 terletak pada orde 3 dengan 3 jumlah knot yaitu pada titik knot 10099,89 ; 10316,38 ;

10606,31. Pada perusahaan Akasha Wira Internasional nilai GCV minimum sebesar 620822 terletak pada orde 2 dengan 4 jumlah knot yaitu pada titik knot 9879,97 ;

10006,65 ; 10099,89 ; 10316,38.

Nilai MAPE untuk PT. Mandom Indonesia sebesar 9,62% < 10% sehingga model yang diperoleh sangat akurat untuk digunakan dalam menduga harga saham pada nilai kurs 10099,89;

10316,38; dan 10606,31. Nilai MAPE untuk PT. Unilever Indonesia terletak diantara 10% -20% sehingga model yang diperoleh baik untuk digunakan dalam menduga harga saham pada nilai kurs 10099,89; 10316,38; dan 10606,31.

Nilai MAPE untuk PT. Akasha Wira Internasional terletak pada 20% - 50% sehingga model yang diperoleh cukup untuk digunakan dalam menduga harga saham pada nilai kurs 9879,97; 10006,65; 10099,89;dan 10316,38.

Pada penelitian ini pendekatan yang digunakan untuk memodelkan nilai kurs terhadap saham pada data longitudinal hanya menggunakan regresi spline truncated, diharapkan pada penelitian selanjutnya menggunakan basis fungsi spline yang lainnya seperti penalized spline.

DAFTAR PUSTAKA

Agustina dan Sumartio, F. 2014. Analisa Faktor-Faktor Yang Mempengaruhi Pergerakan Harga    Saham Pada Perusahaan

Pertambangan.  Jurnal Wira Ekonomi

Mikroskil, 4 (1), pp.51-61.

Bank Indonesia, 2018.

https://www.bi.go.id/id/moneter/kalkulator-kurs/Default.aspx, Diakses tanggal 24 Oktober 2018.

Budiantara, I N. 2011. Penelitian Bidang Regresi Spline Menuju Terwujudnya Penelitian Statistika Yang Mandiri Dan Berkarakter. Seminar Nasional FMIPA Undiksha. Singaraja.

Chen, R. J. C., Bloomfield, P. dan Cubbage, F. W. 2007. Comparing Forecasting Models in Tourism. Journal of Hospitality & Tourism Research, 32 (1), pp.03-21.

Eubank, R.L. 1999. Nonparametric Regression and Spline Smoothing. 2nd ed. New York: Marcel Dekker.

Litawati, E.K. dan Budiantara, I N. 2013. Pendekatan Regresi Nonparametrik Spline untuk Pemodelan Laju Pertumbuhan Ekonomi (LPE) di Jawa Timur. Jurnal Sains dan Seni POMITS, 2 (2), pp.123-128.

Muklis, F. 2016. Perkembangan Dan Tantangan Pasar Modal Indonesia. Jurnal Lembaga Keuangan dan Perbankan, 1 (1), pp.64-75.

Suparti, Prahutama, A. dan Santoso, R. 2017.Kajian Pemodelan Spline Untuk Data Longitudinal Sebagai Perkembangan Dari Regresi Nonparametrik. Seminar Nasional Pendidikan, Sains dan Teknologi. FMIPA Universitas Muhammadiyah Semarang.

Toruan, R. L. 2018. Pengujian Hipotesis Simultan Parameter Model Regresi Nonparametrik Spline Truncated Pada Data Longitudinal (Aplikasi pada Data Pertumbuhan Ekonomi Provinsi Papua Tahun 2011-2016). Tesis. Fakultas Matematika, Komputasi, Dan Sains Data. Institut Teknologi Sepuluh Nopember. Surabaya.

Yahoo Finance, 2018. https://finance.yahoo.com. Diakses tanggal 24 Oktober 2018.

263