POLICY VALUES ASURANSI JOINT LIFE SUAMI ISTRI DENGAN METODE PROSPEKTIF
on
E-Jurnal Matematika Vol. 8(2), Mei 2019, pp.122-131
DOI: https://doi.org/10.24843/MTK.2019.v08.i02.p243
ISSN: 2303-1751
POLICY VALUES ASURANSI JOINT LIFE SUAMI ISTRI DENGAN METODE PROSPEKTIF
I Wayan Sandy Bayu Nugraha1§, Ketut Jayanegara 2, I Nyoman Widana3
1Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: sandybayu73@yahoo.com]
2Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: ktjayanegara@unud.ac.id]
3Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: widana@unud.ac.id]
§Corresponding Author
ABSTRACT
Policy values are funds be held by insurance company that will be used for unexpected claims from insurance participants. The purpose of this work is to calculate constant annual premiums with and without pure endowment on joint life couple insurance, then determine and calculate formula policy values with prospective method. The policy values in joint life couple insurance, are affected by premium payments. Policy values benefit at the end of the 1st year until the end of the 11th year will increase, because the money received by insurance company from premium payments is more than the sum insured to be paid. Policy values benefit at the end of the 11th year until the end of the 66th year will decrease because there are no more premium payments.
Keywords: policy values, premium payments, prospective method
Secara konseptual asuransi merupakan pemindahan risiko dimana pihak tertanggung mengikatkan diri dalam bentuk kontrak polis kepada pihak perusahaan asuransi. Pihak tertanggung wajib membayarkan premi kepada pihak perusahaan, sedangkan pihak perusahaan asuransi wajib memberikan uang pertanggungan jika pihak tertanggung mengalami musibah yang timbul dari suatu peristiwa yang tidak dapat diprediksi di masa depan (Futami, 1993).
Setiap peserta asuransi diwajibkan membayar premi kepada pihak perusahaan asuransi. Premi merupakan sejumlah uang yang harus dibayarkan oleh peserta asuransi kepada perusahaan asuransi sesuai dengan kontrak yang telah disetujui. Pada awal kontrak asuransi, pembayaran klaim yang oleh perusahaan asuransi kepada peserta asuransi jumlahnya lebih sedikit dibandingkan dengan pembayaran premi yang diperoleh. Sehingga, pendapatan perusahaan asuransi harus disimpan sebagai policy values.
Menurut Destriani & Mara (2014), perusahaan jasa asuransi tidak sedikit yang
mengalami kerugian karena tidak mampu membayar klaim kepada peserta asuransi. Hal ini disebabkan ketika jumlah klaim yang harus dibayarkan melebihi jumlah klaim yang diprediksi sebelumnya. Keadaan seperti ini dapat diantisipasi jika perusahaan jasa asuransi memiliki dana policy values yang telah diperhitungkan dengan tepat.
Policy values merupakan sejumlah uang yang ada pada perusahaan asuransi dalam jangka waktu pertanggungan. Perhitungan policy values terbagi menjadi dua yaitu perhitungan policy values prospektif dan retrospektif (Futami, 1993)
Penelitian ini bertujuan menghitung premi tahunan konstan dengan dan tanpa endowment murni pada asuransi jiwa joint life pasangan suami istri, kemudian menentukan dan menghitung formula policy values pada asuransi jiwa joint life pasangan suami istri dengan metode prospektif.
Penelitian Yosia (2016) mengenai perhitungan policy values retrospektif menyatakan bahwa besarnya policy values akan
mengalami peningkatan saat pembayaran premi masih dilakukan. Ketika tidak ada lagi pembayaran premi, besarnya policy values akan menurun karena perusahaan asuransi sudah tidak menerima pembayaran premi.
Sebelum dilakukan perhitungan policy values prospektif, terlebih dahulu dihitung nilai premi tahunan konstan dengan dan tanpa endowment murni pada asuransi joint life pasangan suami istri. Perhitungan premi konstan dipengaruhi oleh faktor tingkat suku bunga dan tingkat mortalitas.
Bunga majemuk adalah pehitungan bunga yang besar pokok selanjutnya merupakan besar pokok sebelumnya di tambah dengan besar bunga (Futami, 1993).
Besar pokok sejumlah P diinvestasikan, tingkat bunga i per tahun, dan jangka investasi n tahun. Sesudah satu tahun, total pokok beserta bunganya adalah:
Pi = + Pi = (1+i),
Pada tahun kedua pokok beserta bunganya menjadi:
P2 = + iPi
= (1+i)+iP(1+i)
= (1+i)(1+i)
= (1+i)2
Sehingga sesudah n tahun total pokok beserta bunganya adalah (Sembiring, 1986):
Pn = (1+i)n (1)
Faktor (1+i)n disebut faktor akumulasi
dan P= (1+i) -n menyatakan besar pokok
beserta bunganya. Bentuk (1+i) disimbolkan
dengan v (Sembiring 1986):
1
V=
1+i
(2)
Menurut Futami (1993), tabel mortalitas merupakan tabel observasi mengenai peluang tingkat kematian berdasarkan kelompok umur. Fungsi-fungsi utama dalam tabel mortalitas adalah:
dγ
dengan, Ix merupakan banyaknya individu yang berhasil mencapai usia tepat X tahun, dx merupakan banyaknya individu yang
meninggal antara umur x tahun sampai X+1 tahun, cIx merupakan peluang individu berumur X meninggal dalam kurun waktu 1 tahun, dan Px merupakan peluang individu berumur X mencapai umur X+1 tahun.
Fungsi gabungan yang menyatakan banyaknya orang berusia X tahun yang masih hidup dikalikan dengan banyaknya orang berumur y tahun yang masih hidup dinotasikan dengan ^xy . Peluang orang berusia X tahun dan y tahun akan tetap hidup selama 1 tahun dinotasikan dengan Pxy . Peluang orang berusia X tahun dan y tahun akan tetap hidup selama t tahun dinotasikan dengan tPxy dan dirumuskan sebagai berikut:
„ „ ⅛+ι ⅛+ι ^xy+ι
L x 'y ^xy
lχ+tlχy+t
L x 'y ^xy
Peluang salah satu di antara X dan y meninggal dalam jangka waktu 1 tahun dinotasikan dengan Pxy dan dirumuskan sebagai berikut:
‰ =1-Pxy=1-(lχy+l)=lχy - Ixyx1 (9)
∖ lχy J lχy
Menurut Bowers Jr & Newton L. (1997), Asuransi jiwa berjangka n tahun adalah asuransi jiwa untuk orang berumur x tahun dengan benefit sebesar 1 satuan yang diberikan jika peserta asuransi meninggal dalam kurun waktu n tahun dinotasikan dengan A1χ-| yang dirumuskan dengan:
: |=∑Vt+1 tPx Vx+t (10)
: |
t=0
Nilai sekarang dari pembayaran yang dilakukan di awal tahun dan ditunda selama n tahun untuk status single life dan joint life dirumuskan dengan:
∞
n| ̈X =∑Vt tPx (11)
t=0 ∞
n| ̈ xy=∑Vk kPxy (12)
k=n
Nilai sekarang dari benefit pada endowment murni berjangka n tahun dengan status joint life yang dibayarkan apabila peserta
asuransi (X,y ) masih hidup sampai kontrak asuransi berakhir dapat dirumuskan sebagai berikut:
^xy: ̅̅̅| = Vn npxy
(13)
Asuransi jiwa berjangka n tahun dengan benefit meningkat pada status joint life adalah asuransi jiwa dengan benefit terus meningkat sebesar 1 satuan setiap tahunnya. Benefit
dibayarkan jika salah satu peserta (x,y)
meninggal dalam kurun waktu n tahun dan
diberikan di akhir tahun kematian peserta asuransi, dirumuskan dengan:
( IA ) xy:̅̅̅| =∑(t+1)V tPxy Qxy+t (14)
t=0
Besarnya premi tahunan konstan dengan endowment murni yang harus dibayarkan oleh
peserta asuransi ialah sebagai berikut:
Q Aχy: ̅̅̅| + Rχ n | ̈x nQy + Ry n | ̈y nQx ̈ xy:̅̅̅| -(IA ) :̅̅̅|
(15)
Sedangkan besarnya premi tahunan konstan tanpa endowment murni yang harus
dibayarkan oleh peserta asuransi ialah sebagai berikut:
■x n| ̈•x nQy + Ry n | ̈y nQx ̈ xy:̅̅̅| - ( IA ) xy :̅̅̅|
(16)
(Matvejevs & Matvejevs, 2001)
Penelitian ini menggunakan data dari Tabel Mortalitas Indonesia 2011. Pengolahan data pada penelitian ini menggunakan Software Microsoft Excel 2013. Adapun langkah -langkah yang dilakukan dalam penelitian ini adalah:
-
4. Menghitung policy values asuransi joint life pada pasangan suami istri dengan menggunakan metode prospektif.
-
5. Interpretasi hasil.
Nilai tabel mortalitas joint life pasangan suami istri dengan i=5%, n=10, x=50 dan y=45, disajikan pada Tabel 1.
Tabel 1. Nilai Tabel Mortalitas Joint Life.
|
n |
Vn |
TlPx |
nPy |
nPx,y I |
TlQx,v \ |
|
1 |
0.9523 |
0.9946 |
0.9980 |
0.9927 |
0.0072 |
|
2 |
0.9070 |
0.9885 |
0.9959 |
0.9844 |
0.0155 |
|
3 |
0.8638 |
0.9815 |
0.9935 |
0.9752 |
0.0247 |
|
10 |
0.6139 |
0.9115 |
0.9668 |
0.8813 |
0.1186 |
Sumber: data diolah, 2019
Untuk Tl=1 didapatkan nilai sebagai berikut:
Vn = (1) =( 1 )= 0,95238
1+ 1+0,05
TlPx = =1-Q50 = 0,99462
nPy = =1-Q45 = 0,99807
TlPx,y= ,45
= ․ 1P45 = 0,99462 ․0,99807=0,99270
TlQx,y = 1- TlPx,y =1- iPso,45 = 0,0072
Ditentukan formula premi tahunan konstan untuk lama kontrak asuransi 1 tahun.
Q ^so,45 : ̅| + ^X 1 | ̈50 1<745 + Ry 1 | ̈45 1QSO
̈50,45: ̅| -(IA )50,45: ̅|
kemudian ditentukan nilai setiap elemen dalam formula dimulai dari menentukan nilai sekarang dari endowment murni berjangka tiap tahun dengan status joint life menggunakan persamaan (13).
^50 ,45 : ̅| = V1 1P50,45 dengan
1P50,45 =
4» , 45: ̅| =(1+0,05) . iPso 1P45
=(1+10,05) . 0,9946 . 0,9980
= 0,9523 . 0,9927
= 0,9454
Nilai sekarang dari benefit tersebut disajikan pada Tabel 2.
Tabel 2. Benefit Endowment murni Joint Life
|
n |
Q |
^50 ,45: ̅̅̅| |
|
1 |
1 |
0.9454 |
|
2 |
1 |
0.8929 |
|
3 |
1 |
0.8424 |
|
10 |
1 |
0.5410 |
Sumber: data diolah, 2019
Kemudian ditentukan nilai sekarang dari pembayaran yang dilakukan di awal tahun dan ditunda selama 1 tahun status single life menggunakan persamaan (11) disajikan pada Tabel 3.
61
1| ̈ so=∑Vn np50 n=l
= + V2 2^50 + ^33Pso+⋯
+ ^61 61?50
=(1+0,05) ιPso + (1 + 0,05) 2p5o
+ (1 + 0,05) 3pso+⋯
+ (1 + 0,05) 61P≡0
= 0,9472+ 0,8966+ 0,8479+⋯+ 6,8021
= 13,5850
66
1| ̈ « =∑Vn nP45 n=l
= + V2 2P45 + V3 3P45 +⋯
+ V61 61P45
=(1+0,05) 1P45 + (1 + 0,05) 2P45
+ (1 + 0,05) 3P45+⋯
+ (1 + 0,05) 61P45
=0,9505+ 0,9033+ 0,8582+⋯+ 5,6652
= 15,6811
Tabel 3. Anuitas Hidup Single Life
|
n |
Rχ |
Ry |
n| ̈ ⅛0 \ |
n| ̈ ⅛5 I |
|
1 |
1 |
1 |
13.5850 |
15.6811 |
|
2 |
1 |
1 |
12.6378 |
14.7306 |
|
3 |
1 |
1 |
11.7412 |
13.8273 |
|
10 |
1 |
1 |
6.7213 |
8.6600 |
Sumber: data diolah, 2019
Kemudian dihitung peluang hidup gabungan status joint life sebagai berikut: TlPso,45 = ιPso,45 = . 1P45
= 0,9946 .0,9980
= 0,9927
Selanjutnya, dihitung nilai sekarang dari pembayaran sebesar 1 satuan yang dilakukan di awal tahun dan ditunda selama 1 tahun status joint life menggunakan persamaan (12) yang disajikan pada Tabel 4.
̈ •50 ,45 : ̅| = ^0 θPsθ,45
1
=(1+0,05) .1=1
Tabel 4. Anuitas Hidup Joint Life
|
n |
̈ ⅛o ,45: ̅| |
|
1 |
1 |
|
2 |
1.9454 |
|
3 |
2.8383 |
|
10 |
7.7813 |
Sumber: data diolah, 2019
Selanjutnya dihitung nilai sekarang benefit yang dibayarkan jika salah satu peserta (X,y) meninggal dalam kurun waktu n tahun, menggunakan persamaan (14) yang hasilnya disajikan pada Tabel 5.
( IA ), :̅|=∑(0+1)v0+1 oPso,45 Qso,45 + 0 k=0
=1 .V1 oPso,45 QSO,45
=1 .0,9523 .1 .0,0073
= 0,0069
Tabel 5. Benefit Pengembalian Premi
|
n |
( IA ) xy:̅̅̅| |
|
1 |
0.0069 |
|
2 |
0.0218 |
|
3 |
0.0457 |
|
10 |
0.5164 |
\ Sumber: data diolah, 2019
Sehingga dapat dilihat besarnya premi tahunan konstan dengan endowment murni menggunakan perhitungan persamaan (15) yang disajikan pada Tabel 6.
Tabel 6. Premi Tahunan Konstan dengan Endowment Murni
|
n |
Premi Tahunan K o ns tan (P ) |
|
1 |
1.0634 |
|
2 |
0.5789 |
|
3 |
0.4199 |
|
. . . |
. . . |
|
10 |
0.2105 |
Sumber: data diolah, 2019
Ditentukan formula premi tahunan konstan untuk lama kontrak asuransi 1 tahun, sesuai dengan persamaan (16). Kemudian dihitung nilai dari masing-masing elemen sesuai dengan perhitungan sebelumnya
Sehingga dapat dilihat besarnya premi tahunan konstan tanpa endowment murni dimulai dari lamanya kontrak 1 tahun hingga lamanya kontrak 10 tahun disajikan pada Tabel 7.
Tabel 7. Premi Tahunan Konstan tanpa Endowment Murni
|
n |
Premi Tahunan K o ns t an (P ) |
|
1 |
0.1113 |
|
2 |
0.1147 |
|
3 |
0.1182 |
|
. . . |
. . . |
|
10 |
0.1361 |
Sumber: data diolah, 2019
Hasil yang didapat pada Tabel 6 dan Tabel 7 disajikan pada Gambar 1.
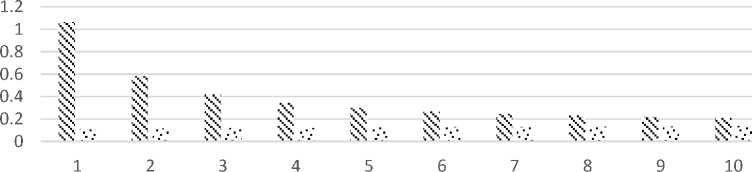
Lamanya kontrak asuransi (n)
Premi tahunan konstan dengan endowment murni Premi tahunan konstan tanpa endowment murni
Gambar 1. Premi tahunan yang bersifat konstan dengan dan tanpa endowment murni untuk lamanya kontrak 1 tahun hingga 10 tahun
Gambar 1 menunjukkan endowment murni yang diberikan untuk peserta asuransi jika kedua peserta bertahan hidup sampai kontrak
-
3.3 Premi Tahunan Konstan Berdasarkan
Usia Peserta Saat Mengikuti Asuransi
Ditentukan formula premi tahunan konstan.
Q A S 0,45 : 3^ + Λx 1 0∣⅛5 O 10^4 S + Ry 10∣⅛4 S 1 θQ S O ¾ 0,45 :lt>| - (1A)S 0,45 :lt>|
Kemudian ditentukan nilai setiap elemen dalam formula sesuai dengan perhitungan pada
berakhir (Q) menyebabkan premi asuransi menjadi lebih mahal.
formula sebelumnya. Sehingga dapat dilihat besarnya premi tahunan konstan dengan endowment murni dengan usia perserta saat mengikuti asuransi dimulai dari 50 tahun untuk suami dan 45 tahun untuk istri hingga usia perserta 59 tahun untuk suami dan 54 tahun untuk istri pada Tabel 8.
Tabel 8. Premi Tahunan Konstan dengan Endowment Murni
|
X |
y |
Premi Tahunan K0ns tan (P') |
|
50 |
45 |
0.2105 |
|
51 |
46 |
0.2220 |
|
52 |
47 |
0.2336 |
|
. . . |
. . . |
. . . |
|
59 |
54 |
0.3215 |
Sumber: data diolah, 2019
Ditentukan premi tahunan konstan.
P _ ^X 1 o∣⅛O 1 0Q4 5 + ^y 1 O∣⅛ 5 1 θQθO ⅛ 0,4 5 :10| - ^)50,4 5:10|
Kemudian ditentukan nilai setiap elemen yang terdapat dalam formula sesuai dengan perhitungan sebelumnya. Sehingga dapat dilihat besarnya premi tahunan konstan tanpa
endowment murni dengan usia perserta saat mengikuti asuransi dimulai dari 50 tahun untuk suami dan 45 tahun untuk istri hingga usia perserta 59 tahun untuk suami dan 54 tahun untuk istri pada Tabel 9.
Tabel 9. Premi Tahunan Konstan tanpa Endowment Murni
|
X |
y |
Premi Tahunan Kons tan (P) |
|
50 |
45 |
0.1361 |
|
51 |
46 |
0.1476 |
|
52 |
47 |
0.1594 |
|
. . . |
. . . |
. . . |
|
59 |
54 |
0.2484 |
Sumber: data diolah, 2019
Hasil yang didapat pada Tabel 8 dan 9 disajikan dalam Gambar 2.
0.35
0.3
0.25
0.2
0.15
0.1
0.05
0

(50,45) (51,46) (52,47) (53,48) (54,49) (55,50) (56,51) (57,52) (58,53) (59,54)
Premi tahunan konstan dengan endowment murni
Premi tahunan konstan tanpa endowment murni
Gambar 2. Premi tahunan yang bersifat konstan dengan dan tanpa endowment murni berdasarkan usia saat mengikuti asuransi
Gambar 2 menunjukkan bahwa endowment murni yang diberikan kepada peserta asuransi
jika keduanya bertahan hidup sampai kontrak berakhir membuat premi menjadi lebih mahal.
3.4 Policy Values Endowment murni pada Asuransi Joint Life (Prospektif)
Perhitungan dilakukan dengan nilai P = 0.2105, Q = 1,Λχ = 1,Λy = 1, dan n = 10. Selanjutnya, ditentukan formula policy values benefit pada akhir tahun pertama dirumuskan sebagai berikut:
+p⅛‰n)0y — ly+J + ⅛(ly+J(lχ - 0+J
+ Q -I x+n,y+n
} +
66 1
∑ (T+F^ ^^+^)( ly — ly+") + fiy( l++^x l-
—
φ
* =[∑(T+⅛
'-a=m
—
((α + 1)P(O+. P ■ l x+a, ^y+a ^ +
—
)
(1 + 0
Untuk, m = 1,2,3 ... ,9
km = Iχ+m,ly+m+ Iχ+m( ly — ly+m) + ly+m (k - lχ+m)
Sehingga diperoleh hasil penyelesaian nilai
policy values untuk akhir tahun pertama adalah sebagai berikut:
1K
= [∑
1
(1 + i)
- 0,2105. ^50+α ,
(a + 1)0,2105(l, (
)
-
‰5+α+l)
(1 + 0,05)
1
(1 + 0 05) ξ {1(912)(1000 - 967) + 1(967)(1000 - 912) (+, )
1
+ (1 + 0,05) 10-1 {1( ,)(U5
-
^45 + 10)
+ 1.912,967}
66
+ ∑ (1 + 0 05)10 (1(899)(1000 - 967) + 1(961)(1000
(1 + 0,05)
+ 1(^45 + 10)(Uo 66
-
^50+10)+1.^50+10 ,45 + 10}
- 912))
+ ∑ (1 + 0,05) (1(^50+/?)(U5
1
912,967 + 912(1000 - 967) + 967 (1000 - 912)
-
, +i (I ≈
, + (
= [ ∑ (
∖a=m
-
-
I)+1(^45+/?)(Uo
1
^45 + 1)+ ^45 + 1 (k
2491939,386
897940,6473
-
^50+l)
= 2,7751
(1+ 1)0,2105(995 .998-989 . 996) (1 + 0,05)
Jadi policy values t = 10 adalah sebesar
2,7751. Selanjutnya sesuai dengan kontrak
- 0,2105 .995 .998 )
dalam penelitian ini ditentukan formula policy
1
+ (1 + 0,05)9 {1(912)(1000 - 967)
+ 1(967)(1000 - 912) + 1. 912 . 967}
66
+ ∑ (1 + 0,05) 10 (1(899)(1000 - 967)
values untuk akhir tahun ke 11 sampai akhir
tahun ke 66 adalah menggunakan formula
sebagai berikut:
+ 1(961)(1000
- 912))]
1
995,998 + 995(1000 - 998) + 998 (1000 - 995)
[
∑ (1 + 1)β-m (Rx ( lχ+β)(Iy - ^y+n )
219569,9415
= 999989,6166
= 0,2195
+ Ry (ly+β)(I.
-
■x+n))] 1
υn+t
Sehingga dana policy values pada tahun pertama yaitu untuk t = 1 adalah sebesar 0,2195. Perhitungan policy values dari tahun pertama sampai tahun ke sembilan menggunakan formula yang sama karena sesuai dengan kontrak yang telah dijelaskan sebelumnya.
Selanjutnya sesuai dengan kontrak dalam penelitian ini ditentukan formula policy values pada akhir tahun ke 10 adalah sebagai berikut:
uJ = ( ly - ^y+n)+ ly+J (l.
-
^x+n)
untuk j= + 1, n + 2, n+3,…
Sehingga diperoleh hasil penyelesaian nilai policy values untuk akhir tahun ke 66 adalah sebagai berikut: 10+56^
[
∑ (1 + 0,05)11-10 (1(Uo+11)(Us
+1(Us + 11)(Uo
-
Us + 10)
-
Uo+10))]
1
=[
1
⅛+66 (Us - Us+io)+ Us + 66 (Uo
-
Uo+io)
(1 + i) 10-1
{1(^50+10)(U5
-
^45 + 10)
+ 1(^45 + 10)(⅛ 66
+ ∑ (1+1)
-
^50+10)+1.^50+10 ,45 + 10}
(1(^50+11)(U5
-
•45+10)+1(^45 + 11)(⅛
[
∑ (1+0,05)1 (1(899)(1000 - 967)
+ 1(961)(1000
-
^50+10)) h—
,
+ ^50+10(^45
-
1
^45+10)+ ^45 + 10 (⅛
-
^50+10)
Sehingga diperoleh hasil penyelesaian nilai policy values untuk akhir tahun ke 10 adalah sebagai berikut:
1
0(1000 - 967) + 0,01(1000 - 912)
Jadi dana policy values untuk t = 66 adalah sebesar 1. Dengan menggunakan perhitungan Microsoft Excel 2013 diperoleh nilai policy values pada asuransi joint life dengan endowment murni menggunakan metode prospektif disajikan pada Tabel 10.
Untuk, m = 1,2,3,... 9.
km = l x a m,ly a m+ l x a m( ly — ly a m) + ly a m (lx - lxa m)
Sehingga diperoleh hasil penyelesaian nilai policy values untuk akhir tahun pertama adalah sebagai berikut:
Tabel 10. Policy Values Asuransi Joint Life Endowment murni (Prospektif)
V
|
t |
V |
t |
V |
t |
V |
|
1 |
0.2195 |
23 |
10.3597 |
45 |
4.3315 |
|
2 |
0.4498 |
24 |
10.0628 |
46 |
4.1258 |
|
3 |
0.6915 |
25 |
9.7656 |
47 |
3.8947 |
|
4 |
0.9452 |
26 |
9.4672 |
48 |
3.6554 |
|
5 |
1.2118 |
27 |
9.1683 |
49 |
3.4229 |
|
6 |
1.4922 |
28 |
8.8700 |
50 |
3.2089 |
|
7 |
1.7875 |
29 |
8.5731 |
51 |
3.0308 |
|
8 |
2.0988 |
30 |
8.2787 |
52 |
2.8848 |
|
9 |
2.4275 |
31 |
7.9868 |
53 |
2.7798 |
|
10 |
2.7751 |
32 |
7.6977 |
54 |
2.6410 |
|
11 |
13.6737 |
33 |
7.4107 |
55 |
2.4903 |
|
12 |
13.4269 |
34 |
7.1254 |
56 |
2.3452 |
|
13 |
13.1748 |
35 |
6.8414 |
57 |
2.2050 |
|
14 |
12.9167 |
36 |
6.5587 |
58 |
2.0704 |
|
15 |
12.6524 |
37 |
6.2840 |
59 |
1.9422 |
|
16 |
12.3818 |
38 |
6.0183 |
60 |
1.8224 |
|
17 |
12.1051 |
39 |
5.7584 |
61 |
1.7129 |
|
18 |
11.8223 |
40 |
5.5043 |
62 |
1.6117 |
|
19 |
11.5358 |
41 |
5.2564 |
63 |
1.5158 |
|
20 |
11.2455 |
42 |
5.0059 |
64 |
1.4152 |
|
21 |
10.9520 |
43 |
4.7681 |
65 |
1.2822 |
|
22 |
10.6560 |
44 |
4.5428 |
66 |
1 |
Sumber: data diolah, 2019
■ ∑
—
1
(1 + 0 1 - 1
C
■(1 + 1)0,2105⅛aa,⅛aa
0,2105+ 5 0 aa, ∣4 5 a a )
1
+ (1 + 0,05)10-1
{1⅛0a10,)‰5
—
—
(1 + 0,05)
∕50aaa√45aaa1)
l4 5a 10 ) + 1(‰ 5 a 1O)( l 5 0 — l 50a10)}
66 +∑ /3=11
—
______1______
(1 + 0,05)10( ( 50 aβ ) 4 5
⅛0+10.
’)) Γ^
L50 + 1, l4
L50 + 1, ‘45 + 1
1
—
) + 1( )(
+ ⅛0 + 1(45 ^5+ι) + ^45+1 (50
[10 - 1 1 Z
∑<τ⅛(-a=l
—
50+1)
(1 + 1)0,2105(995 ■ 998 — 989 ■ 996) (1 + 0,05)
— 0,2105.995 .998 )
1
+ 7TT7Γ^{1(912×1000 — 967) + 1(967)(1000 — 912)}
(1 + 0,05)
66 +∑ /3=11
1
m , nnςv0 (1(899)(1000 — 967) + 1(961)(1000 (1 + 0,05)
— 912))]
1
995,998 + 995(1000 — 998) + 998 (1000 — 995)
141870,1871
9999 89,6166
0,1418
3.5 Policy Values tanpa Endowment murni Asuransi Joint Life (Prospektif)
dengan nilai P = 0,1361, XXx ■ 1,Ry ■ 1, dan n = 10. sehingga policy values benefit
pada akhir tahun pertama dapat sebagai berikut:
dirumuskan
Sehingga dana policy values untuk t ■ 1 adalah sebesar 0,1418. Perhitungan policy values dari tahun pertama sampai tahun ke sembilan menggunakan formula yang sama sesuai dengan kontrak. Selanjutnya ditentukan formula policy values pada akhir tahun ke 10 adalah sebagai berikut: wv
-
In - 1
∑
a=m
1 ((a + 1)P( l
(1 + i)a - m (
■x+a, yy+a
-
lx+a+1, ly+a+1)
(1 + i )
k ■ lxa a, ly+a
1
(1 + O
)
{RxGxaJ(ly
-
ly+n )
+ Ry( Iyan)(lx - lx a n)}
66
∑1
(1 + i)β- m (Rx(Xχaβ)( ly - lya n) β=n+ιv 1
+ Ry(ly + β)(l
-
'x+n ))∖km
■l
1
(1 + i)10- 1 {1(^ 5 0a 10 )(l45
+ 164 5 a1 0)(i 5 0
66
—
50a10)}
—
⅛ a10 )
+ Σ (1 + i) 1 1 - 1(1^ 5 0 a 1 1)( l 4 5
—
—
-4 5 a 1 0 ) + 1( l 4 5 a 1 1)( l 5 0
l50a10)) 1 1 . 1 Zl
l5 0 a 1 0, l4 5 a 1 0+ i5 0 a 1 0( i4 5
—
1
)+ (
—
l50a10)
Sehingga diperoleh hasil penyelesaian nilai policy values untuk akhir tahun ke 10 adalah sebagai berikut:
1
—— {1(912)(1000 — 967) + 1(967)(1000 — 912)} ( -L I ∖J f∖J ) J
Tabel 11. Policy Values Asuransi Joint Life tanpa Endowment Murni (Prospektif)
66
+ Σ —-?7^(1(899)(1000 — 967) + 1(961)(1000
(+, )
— 912))
1
912,967 + 912(1000 - 967) + 967 (1000 - 912)
1610608,863
897940,6473
= 1,7936
Jadi dana policy values t = 10 adalah sebesar 1,7936. Selanjutnya sesuai dengan kontrak ditentukan formula policy values untuk akhir tahun ke 11 sampai akhir tahun ke 66 adalah menggunakan formula sebagai berikut:
66
β=n+l
—
Iy+n ) + Ry( Iy+/?)(lx
-
lx+n ))
|
t |
V |
t |
V |
t |
V |
|
1 |
0.1418 |
23 |
10.3597 |
45 |
4.3315 |
|
2 |
0.2907 |
24 |
10.0628 |
46 |
4.1258 |
|
3 |
0.4469 |
25 |
9.7656 |
47 |
3.8947 |
|
4 |
0.6108 |
26 |
9.4672 |
48 |
3.6554 |
|
5 |
0.7832 |
27 |
9.1683 |
49 |
3.4229 |
|
6 |
0.9644 |
28 |
8.8700 |
50 |
3.2089 |
|
7 |
1.1553 |
29 |
8.5731 |
51 |
3.0308 |
|
8 |
1.3565 |
30 |
8.2787 |
52 |
2.8848 |
|
9 |
1.5689 |
31 |
7.9868 |
53 |
2.7798 |
|
10 |
1.7936 |
32 |
7.6977 |
54 |
2.6410 |
|
11 |
13.6737 |
33 |
7.4107 |
55 |
2.4903 |
|
12 |
13.4269 |
34 |
7.1254 |
56 |
2.3452 |
|
13 |
13.1748 |
35 |
6.8414 |
57 |
2.2050 |
|
14 |
12.9167 |
36 |
6.5587 |
58 |
2.0704 |
|
15 |
12.6524 |
37 |
6.2840 |
59 |
1.9422 |
|
16 |
12.3818 |
38 |
6.0183 |
60 |
1.8224 |
|
17 |
12.1051 |
39 |
5.7584 |
61 |
1.7129 |
|
18 |
11.8223 |
40 |
5.5043 |
62 |
1.6117 |
|
19 |
11.5358 |
41 |
5.2564 |
63 |
1.5158 |
|
20 |
11.2455 |
42 |
5.0059 |
64 |
1.4152 |
|
21 |
10.9520 |
43 |
4.7681 |
65 |
1.2822 |
|
22 |
10.6560 |
44 |
4.5428 |
66 |
1 |
Sumber: data diolah, 2019
U∏+t
Uj = U+;(ly — ly+„)+ ly + ; ( U untuk j = n+1,n + 2,n + 3,^
-
lx+n )
Sehingga diperoleh hasil penyelesaian nilai policy values untuk akhir tahun ke 66 adalah sebagai berikut:
10+S6^
16 6 1
∑s6<1 + 0,05) 1 1 - 1O <1°s o+1 1)°4 s
+ 1<U s+1 1)< I s O
—
Us + IO )
—
ls o+1 o)) ; (Γ
50+66 ( 45
1
—
145+10) + ^45+66(^50 ⅛0+10)
16 6
∑ ..,.∙<' ■■■<"■•• --'
+ 1<961)<1000
— 912))]
1
0(1000 — 967) + 0,01(1000 — 912)
_ 0,501144307
= 0,501144307 = 1
Jadi dana policy values t = 66 adalah sebesar 1. Diperoleh nilai policy values pada asuransi joint life tanpa endowment murni menggunakan metode prospektif disajikan pada Tabel 11.
4. KESIMPULAN DAN SARAN
Besarnya policy values benefit pada asuransi joint life endowment murni untuk t = 1 adalah sebesar 0,2195. Nilai ini mengalami peningkatan hingga akhir tahun ke 11, sehingga nilai policy values benefit untuk t = 11 adalah sebesar 13,6737. Hal ini disebabkan karena uang yang diterima perusahaan asuransi dari pembayaran premi melebihi jumlah uang pertanggungan yang harus dibayarkan.
Sedangkan nilai policy values benefit pada akhir tahun ke 11 hingga akhir tahun ke 66 mengalami penurunan, sehingga nilai policy values benefit untuk t = 66 adalah sebesar 1. Hal ini disebabkan karena sudah tidak ada lagi pembayaran premi namun perusahaan harus tetap membayarkan uang pertanggungan setiap tahunnya.
Hal tersebut juga berlaku pada policy values benefit pada asuransi joint life tanpa endowment murni yaitu untuk, t = 1 nilai policy values benefitnya adalah sebesar 0,1418, kemudian akan meningkat hingga = 11 menjadi sebesar 13,6737, dan nilai policy values benefit akan menurun hingga untuk
t = 66 hingga nilainya menjadi sebesar 1.
Disarankan untuk penelitian selanjutnya dapat meghitung asuransi joint life lebih dari 2 orang seperti, sebuah keluarga yang terdiri dari suami, istri, dan anaknya. Selain itu dapat mengkombinasikan perhitungan policy values prospektif dengan retrospektif.
DAFTAR PUSTAKA
Bowers Jr, Newton L. 1997. Actuarial
Mathematics. 2nd ed. Schaumburg: The Society Of Actuaries.
Destriani, Neva Satyahadewi, and Muhlasah Novitasari Mara. 2014. “Penentuan Nilai Cadangan Prospektif Pada Asuransi Jiwa
Seumur Hidup Menggunakan Metode New Jersey.” Buletin Ilmiah Mat.Stat dan Terapannya (Bimaster) 3(1): 7–12.
Futami, T. (1993). Matematika Asuransi Jiwa, Bagian I (1st ed.). Tokyo: Oriental Life Insurance Cultural Development Center.
Matvejevs, A., and A. Matvejevs. 2001. “Insurance Models for Joint Life and Last Survivor Benefits.” Informatica 12(4).
Sembiring, R. K. (1986). Buku Materi Pokok Asuransi I. Jakarta: Universitas Terbuka.
Yosia, Bella. 2016. Penentuan Premi Tahunan Konstan Dan Cadangan Benefit Pada Asuransi Joint Life. Skripsi. Bogor. Institut Pertanian Bogor.
131
Discussion and feedback