MODEL DINAMIKA PENYEBARAN PENYAKIT CAMPAK DENGAN PENGARUH VAKSINASI DAN PENERAPANNYA DI PROVINSI NUSA TENGGARA BARAT

E-Jurnal Matematika Vol. 8(2), Mei 2019, pp.112-121

DOI: https://doi.org/10.24843/MTK.2019.v08.i02.p242

ISSN: 2303-1751

MODEL DINAMIKA PENYEBARAN PENYAKIT CAMPAK DENGAN PENGARUH VAKSINASI DAN PENERAPANNYA DI PROVINSI NUSA TENGGARA BARAT

Mutmainnah^1§, Lailia Awalushaumi², Qurratul Aini³

¹Program Studi Matematika, Fakultas MIPA – Universitas Mataram [E-mail : mmut855@gmail.com]

²Program Studi Matematika, Fakultas MIPA – Universitas Mataram [E-mail : awalushaumi@yahoo.co.id]

³Program Studi Matematika, Fakultas MIPA – Universitas Mataram [E-mail : qurratulaini.aini@unram.ac.id]

^§Corresponding Author

ABSTARCT

Measles is an acute disease highly contagious, caused the measles. This disease is transmitted through droplet or direct contact to the patient. Besides causing various complications, this disease can also cause death. The purpose of this research was we formulated a model the dynamics of the spread of diseases by the influence of a measles vaccination, that are used to know the influence of vaccination to the spread of diseases measles in the province of NTB. The dynamics model of the spread of diseases by the influence of a measles vaccination,

^dS =(1-θ)∏-^αSI -µS

dt           N

dI dt

αSI N

- µI - µ_t I - βI

dV dt

= θ∏ + βI - µV

Based on a implementation model in NTB Province we get bigger the scope of vaccination done in the NTB so the less individuals are susceptible when stability and measles disease faster disappearance.

Keywords: dynamic model,measles of NTB, vaccination

• 1    PENDAHULUAN

Penyakit campakdikenal juga sebagai Measlesmerupakan penyakit infeksi akut, kebanyakan menyerang anak-anak dan disebabkan oleh virus (WHO, 2004). Penyakit ini disebabkan oleh Measles virus (MV), genus virus Morbili family Paramyxoviridae(Depkes, 2008). Penyakit ini dapat disertai dengan komplikasi pneumonia, diare, meningitis dan bahkan dapat menyebabkan kematian (Depkes, 2017). Menurut Badan Pencegahan dan Pengendalian Penyakit Indonesia (2016), 90% orang yang berinteraksi erat dengan penderita dapat tertular jika mereka belum kebal terhadap campak. Sedangkan seseorang dapat kebal, jika telah divaksinasi atau pernah terinfeksi virus campak sebelumnya. Menurut Chin (2000), vaksinasi dapat menaikkan tingkat imunitas sampai sekitar 99%. Dengan program vaksinasi

yang efektif untuk bayi dan anak-anak kasus campak dinegara seperti Amerika dan Kanada turun sebesar 99%. Vaksinasi merupakan upaya yang efektif dalam mencegah dan memberantas penyakit campak.

Model matematika yang menjelaskan penyebaran penyakit campak telah banyak dikonstruksi dandidiskusikan dengan batasan-batasan masalah yang berbeda. Model penyebaran penyakit inidikonstruksi melalui beberapa pendekatan, seperti Verguet, dkk., (2017) yang mengkonstruksi model penyebaran penyakit campak dengan membangun model dinamis transmisi campak di India dengan parameter yang secara empiris disimpulkan menggunakan analisis spektral dari serangkaian waktu kematian campak. Model ini kemudian digunakan untuk memperkirakan CFR (case fatality rate) campak, jumlah kematian campak,

dan dampak vaksinasi, pada tahun 2000–2015 di India dan di negara bagian Bihar dan Uttar Pradesh (UP).

Selain itu ada pula yang menggunakan pendekatan model host seperti model yang dikontruksi oleh Haffernan dan Kelling (2007). Lashari (2016) mengkontruksi model matematika SIR penyakit campak dengan pengobatan, yang merupakan pengembangan dari model SIR klasik, sedangkan Aziziah (2017) mengembangkan model SIR klasik pada penyakit campak dengan memperhatikan vaksinasi. Dalam penelitian ini, model dinamika penyebaran penyakit campak mengacu pada model SIR ditambah vaksinasi denganbeberapa modifikasi yang akan penulis jelaskan di subbab selanjutnya. Adapun tujuan penelitian ini adalah mengetahui model dinamika penyebaran penyakit campak dengan pengaruh vaksinasi dan penerapannya di Provinsi Nusa Tenggara Barat.

Model dinamika penyebaran penyakit campak berbentuk sistem nonlinier. Suatu langkah terbaik dalam memulai menganalisis sistem nonlinear untuk sistem persamaan * = f(x) adalah menentukan titik tetap dari sistem persamaan X = f(x) dan menjelaskan perilaku X = f(x) disekitar titik tetap.

Definisi 1.1 Titik x₀ ∈ Kⁿdisebut titik tetap atau titik kritis dari Sistem Persamaan x = f(x) jika f (x₀) = 0(Perko, 2001).

Sifat kestabilan pada titik tetap berdasarkan nilai eigen menurut Boyce dan Diprima (2012),

Tabel 1.1 Sifat Kestabilan Berdasarkan Nilai

Eigen

Nilai Eigen	Kestabilan
Riil berbeda,	• Stabil asimtotik untuk setiap
bertanda sama	nilai eigen bernilai negatif • Tidak stabil untuk setiap nilai eigen bernilai positif
Riil berbeda, berlawanan tanda	Tidak stabil
Riil sama	•    Stabil asimtotik untuk setiap nilai eigen bernilai negatif •    Tidak stabil untuk setiap nilai eigen bernilai positif
Kompleks	• Stabil asimtotik untuk
sekawan bukan	bagian real negatif
imajiner murni	• Tidak stabil untuk bagian real positif
Imajiner murni	Stabil

• 2    HASIL DAN PEMBAHASAN

Model dinamika penyebaran penyakit campak ini mengacu pada model SIR yang dipaparkan oleh Aziziah (2017)    dalam

penelitiannya, tetapi dengan empat modifikasi. Modifikasi tersebut terletak pada populasi Recovered (sembuh) yang diganti dengan populasi Vaccinated(vaksinasi). Modifikasi pada kompartemen tersebut dilakukan karena pada penelitian ini akan dilihat pengaruh vaksinasi terhadap penyebaran penyakit campak, sehingga kelompok individu yang sembuh diganti dengan kelompok individu yang divaksinasi. Modifikasi juga dilakukan dengan penambahan laju kematian akibat penyakit. Penambahan ini mengacu pada penelitian Hethcote (2000), yang menyatakan bahwa laju kematian akibat penyakit mempunyai pengaruh terhadap jumlah populasi. Modifikasi selanjutnya terletak pada laju kelahiran dan laju kematian alami yang diasumsikan tidak sama. Hal ini mengacu pada pernyataan Mantra (2006) dalam bukunya yang berjudul Demografi Umum, yang mengatakan bahwa laju kelahiran lebih kompleks daripada laju kematian, karena seorang perempuan hanya meninggal satu kali, tetapi ia dapat melahirkan lebih dari seorang bayi. Dan modifikasi selanjutnya terletak pada laju infeksi yang bergantung pada total populasi (N) (Hethcote, 2000).

Adapun asumsi untuk menyederhanakan atau mengurangi jumlah faktor yang mempengaruhi model, antara lain : a. Populasi penduduk bersifat tertutup.

• b.    Populasi rentan bersifat homogeny, asumsi ini sesuai menurut Depkes (2008), bahwa 90% individu yang rentan terhadap penyakit campak, akan terserang penyakit campak.

• c.    Hanya individu yang terinfeksi yang mengalami kematian akibat penyakit campak.

• d.    Laju infeksi dari populasi rentan ke populasi infeksi terjadi karena adanya kontak antara individu rentan dan individu infeksi (Cherry, dkk., 2014).

• e.    Menurut Chin (2000), vaksinasi dapat menaikkan tingkat imunitas sampai 99%.

  Maka dari ini, diasumsikan keampuhan vaksin mencapai 100%.

  • f.    Kekebalan yang terjadi karena vaksin bersifat permanen.

  • g.    Pengendalian dengan selain vaksin diabaikan.

  • h.    Saat vaksinasi, individu dalam keadaan sehat.

  • i.    Penyakit selain campak diabaikan.

  Berikut diagram alir penyebaran penyakit campak dengan vaksinasi:

  
  

  β

  
  

  θ

  
  

  laju kesembuhan penyakit campak

  
  

  cakupan vaksinasi

  
  
  

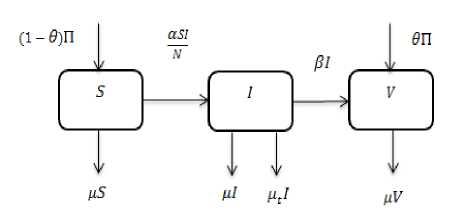
  Gambar1. Diagram alir model dinamika penyebaran penyakit campak dengan pengaruh vaksinasi

  
  

  dengan,  μ,α,β > 0,  0 ≤ θ ≤ 1 dan

  S, I, R ≥ 0

  Dari sistem persamaan (1) diperoleh

  dN  dS  dI  dV

  1

  dt   dt   dt   dt

  • - ∏-μS - μI - μ_tI - μV

  • - ∏-μ( S +1 + V) - μ_tI

  • -    ∏-μN-μ_tI ≤ ∏-μN

  Sehingga, diperoleh

  dN

  -∏- μN

  dt

  dN

  -------- dt

  ∏ -μN

  dN

  ∫--------- dt

  ^j∏- μN  ^J

  
  

  Berdasarkan diagram alir pada gambar 1 model dinamika penyebaran penyakit campak dengan vaksinasi dapat diekspresikan sebagai berikut:

  
  

  n c

  N(t) -∏-Ce-^μt μ μ

  Akan ditunjukkan N(t) → ∏ untuk μ

  
  

  t → ∞

  
  

  dS

  • —    ^- (1^- θ) ∏^--^-μ

  dtN

  dI

  • —    =--μI - μ I - βI

  dt N

  --= θ∏+ βl - μV dt

  dimana:

  
  

  (∏

  lim N^(t) ^- lim —

  
  

  t →∞

  
  

  t →∞

  
  

  < μ

  
  

  —

  
  

  C

  e

  μ

  
  

  μ

  
  

  J

  
  

  (1)

  
  

  ∏   C

  - lim ^- lim e ^μ t→∞ μ   t→∞ μ

  ∏

  
  

  Laju perubahan jumlah individu rentan dt

  
  

  Laju perubahan jumlah individu infeksi

  
  

  dt

  
  

  Laju perubahan jumlah individu divaksinasi

  S   Populasi rentan (Susceptable)

  I   Populasi infeksi (Infected)

  R  Populasi sembuh (Recovered)

  • ^μ   laju kematian alami

  • α   laju infeksi penyakit campak

  
  

  μ

  Didapatkan 0 < N(t) ≤ ∏     menunjukkan

  μ

  jumlah populasi terbatas.Menurut Ngilawajan (2010), laju pertumbuhan penduduk akan terbatas sesuai dengan ketersediaan makanan, tempat tinggal, dan sumber hidup lainnya. Sehingga jumlah populasi dengan model ini akan selalu terbatas pada suatu nilai tertentu. Pada kondisi kesetimbangan (equilibrium), populasi akan akan sama dengan carrying capacitiy, sehingga diperoleh,

  
  

  N = ∏

  μ

  
  

  (2)

  
  

  2.1 Titik Tetap Model Penyebaran Penyakit Campak dengan Pengaruh Vaksinasi

  Berdasarkan definisi (1.1), titik tetap

  
  

  diperoleh jika — = 0, dt

  
  

  dI      dV

  — = 0dan— = 0.

  
  

  dt

  
  

  Sehingga sistem persamaan (1) dapat

  (1 - θ) ∏-^aSI - μS = 0

  
  

  dt ditulis :

  
  

  (3)

  
  

  terinfeksi tidak sama dengan nol (I ≠ 0). Sehingga diperoleh suatu keadaan dimana terdapat individu yang terinfeksi yang dapat menularkan penyakit campak di dalam populasi. Hal ini yang dapat menimbulkan endemik penyakit campak.

  Dengan mensubstitusikan persamaan (7) ke persamaan (3), diperoleh:

  
  

  ^aSI- - μ - μtI - βI = 0

  θ ∏+βI - μV = 0

  Dari sistem persamaan(4.7) diperoleh :

  I = 0

  
  

  (4)

  
  

  (5)

  
  

  _{1 =} α(^{1 -} θ) ∏ ^-μ(μ⁺μt^+β)^N

  ^{1         a}(μ⁺μt^+β)        (₁₀)

  Dengan mensubstitusikan persamaan (10) ke persamaan (5), diperoleh:

  
  

  dan

  
  

  _s = (^μ+μt^+β) ⁿ

  
  

  a

  
  

  (6)

  
  

  (7)

  
  

  2.1.1 Titik tetap bebas penyakit (E ₀)

  Titik tetap bebas penyakit dari model dinamika penyebaran penyakit campak dengan pengaruh vaksinasi, didapatkan jika individu yang terinfeksi adalah nol (I = 0). Sehingga diperoleh suatu keadaan dimana semua individu masuk ke populasi rentan dan populasi vaksinasi, serta tidak ada individu yang menularkan atau terinfeksi penyakit campak.

  Dengan mensubstitusikan persamaan (6) ke persamaan (3), diperoleh :

  _c _ (1 - θ ∏

  S 0 =

  
  

  μ

  
  

  (8)

  
  

  Dengan mensubstitusikan persamaan (4.9) ke

  
  

  persamaan (4.7), diperoleh :

  θ∏

  V o =

  μ

  
  

  (9)

  
  

  Berdasarkan persamaan (4.9), (4.11) dan (4.12), diperoleh titik tetap bebas penyakit campak, yaitu :

  
  

  E o = (S o, I o, V o) =

  
  

  f ^θ^' ,o, θ∏

  
  

  V μ

  
  

  μ 7

  
  

  2.1.2 Titik tetap endemik penyakit (E ₁)

  Titik tetap endemik penyakit dari model penyebaran penyakit campak dengan pengaruh vaksinasi, didapatkan jika individu yang

  
  

  V1 =

  
  

  (μ + μ_t + β‰θ ∏-βμN)+ αβ(1 - θ) ∏

  
  

  αμ(μ⁺μt^+β)

  
  

  Sehingga didapatkan titik tetap endemik penyakit campak, yaitu :

  E1 = (S1,11, V1)

  '(μ + μ + β)∏ α(1 -θ)∏-(μ + μ + β)∏ ' ^aμ ’      α(μ ⁺ μt^{+ β})     ’

  
  

  (μ + μ + β∖aθ ∏- βμN) + αβ(1 - θ) ∏

  -----~—^t---------f-------------⅛--------------

  ’ (μ ⁺ μ_t ^{+ β})

  
  

  V

  
  

  aμ

  
  

  7

  
  

  2.2 Menentukan Bilangan Reproduksi Dasar

  Penyakit Campak (R ₀)

  Menurut Diekmann & Heesterbeek (2000), Bilangan reproduksi dasar ( R₀) merupakan jumlah rata-rata kasus individu rentan yang terinfeksi disebabkan oleh satu individu yang sudah terinfeksi, jika individu yang terinfeksi tersebutmasuk ke dalam populasi yang sebelumnya masih rentan. Jika nilai R₀ < 1 maka banyaknya individu yang terinfeksi penyakit kemungkinan semakin berkurang atau akan hilang dari populasi. Sedangkan jika R₀ > 1, maka banyaknya individu akan terinfeksi semakin meningkat dan penyakit akan menjadi endemik.

  Penentuan nilai menggunakan metode yang diperkenalkan oleh Driessche dan Watmough (2002) yaitu metode matriksnext generation. Pada model yang sudah dibentuk sebelumnya, populasi terinfeksi adalah Infectious atau dengan kata lain satu-satunya

  
  

  populasi yang dapat menularkan penyakit campak, sehingga :

  
  

  dI dt

  
  

  aSI

  N

  
  

  ^- μI ^- μ_t I ^{- β}I

  
  

  Kemudian akan dicari persamaan karakteristik (λ):

  det(J - λI ) — 0       (14)

  
  

  dI dt

  
  

  N -^μ+μ,^{+ β} 'I

  
  

  Berdasarkan metode matriksnext generation, diperoleh :

  
  

  φ =

  
  

  αSI

  N

  
  

  dan ψ = [(μ⁺μt^{+ β}I ]

  
  

  Analisis kestabilan disekitar titik tetap bebas penyakit yaitu dengan mensubstitusikan titik tetap bebas penyakit(F₀) ke persamaan (14), sehingga diperoleh :

  - μ - λ	- α(1 - θ) a(1 - θ)-(μ + μt + β		0
  0		)-λ	0	— 0
  0	β		- μ - λ

  
  

  Dengan F dan V adalah hasil Iiniearisasi dari φ dan ψ, yaitu :

  
  

  (— μ — λ)(α(1 — θ) -(μ + μ + β)-λ)(- μ — λ) — 0

  
  

  F =

  
  

  aS  αSI

  —

  N N²

  
  

  dan

  
  

  V = [μ⁺μt^+β]

  Sehingga diperolehmatriksnext sebagai berikut :

  _-1

  K = FV =

  
  

  Diperoleh nilai eigen untuk titik tetap bebas penyakit adalah :

  λ = -μ

  λ₂ = a(1 - θ)-(μ + μ_t + β) (15)

  
  

  generation

  
  

  aS  aSI

  ---—

  N _N²

  μ ⁺ μ,^{+ β}

  
  

  (11)

  
  

  Selanjutnya mensubstitusi persamaan

  
  

  ((i - θ) ∏ _n θ m

  E₀ =I  -----—,0,----I ke persamaan (11), v μ      μ )

  
  

  sehingga diperoleh bilangan reproduksi dasar

  
  

  penyakit campak(T? ₀)

  
  

  „ _ (1 — θ)α

  R o =        o

  μ⁺μt^{+ β}

  
  

  (12)

  
  

  2.3 Analisis Kestabilan Titik Tetap

  Setelah diperoleh titik tetap, selanjutnya menentukan matriks Jacobian dengan melakukan linierisasi pada sistem persamaan diferensial nonlinier. Dari matriks Jacobian akan didapatkan nilai eigen. Nilai eigen berfungsi untuk mencari kestabilan dari titik tetap pada sistem.Berikut matriks Jacobian dari sistem :

  
  

  λ = -μ

  Titik tetap bebas penyakit akan stabil asimtotik jika semua nilai eigen bernilai negatif. Dari sistem persamaan (15), terlihat nilai λ dan λ bernilai negatif. Sedangkan nilai λ₂ belum pastinegatif maupun positif. Jika λ bernilai negatif, titik tetap bebas penyakit campak akan stabil, namun jikaλ bernilaipositif maka titik tetap bebas penyakit campak akan tidak stabil.

  Agar titik tetap bebas penyakit campak stabil dimisalkan λ₂ < 0

  α(1 - θ) -(μ + μ + β) < 0

  ^{a(1 -}θ -C^μ+^μ+^β_<0
  
  (μ⁺μ_t^+β)  (μ⁺μ_t^+β)

  ^a-θ) -1 < 0
  
  (μ⁺μ_t^+β)

  
  

  a(1 - θ) (μ⁺μ_t^+β)

  
  

  dimana,

  
  

  a(1 - θ) (μ ⁺ μ_t ^{+ β})

  
  

  = R o

  
  

  	Γ a! --+	aSI __f l		aS  aSI --+--	aSI
  	N	2   μ N2		N  N2	Nr
  	aI	aSI	aS	aSI  i	aSI
  —	—	—	—	—τ-(μ+μ+β)	-
  	N	N2	N	N2          t	N2
  		0		β	- μ
  	L

  (13)

  
  

  Maka dapat diperoleh titik tetap bebas penyakit campak akan stabil asimtotik jika r ₀ < 1 yang menunjukkan bahwa pada populasi tidak terjadi penyebaran penyakit. Sedangkan titik tetap bebas penyakit campak akan tidak

  
  

stabil jika R0 > 1 yang menunjukkan akan selalu terjadi penyebaran penyakit di dalam populasi.

Dengan cara yang sama, didapatkan hasil untuk titik tetap endemik penyakit yaitu, αBλ + (μαA + μaB)λ + (μ AB + βμAB + αμAB+μAB²) = 0 dengan,

A = α(1 — θ) — (μ + μ_t + β)

^b = (^{μ +} μ ^{+ β})

Persamaan diatas dimisalkan dengan persamaan berikut,

a o λ ⁺ aι^{λ +} a 2 = 0           ⁽¹⁶⁾

Menurut kriteria Routh-Hurwitz, untuk mendapatkan akar-akar real yang negatif (stabil) haruslah a₀ , _a dan _a bernilai positif.

Misalkan nilai a₀ , a₁ dan a₂ adalah positif, diperoleh,

a 0 = aB > 0

Jelas a₀ adalah positif karena a > 0 dan B = (μ + μ_t + β)> 0.

Untuk, a₁ = μaA + μaB > 0

μa(A + B )> 0

A + B > 0

diperoleh :

a (1 — θ) > 0

Jelas a₁  adalah positif karena a > 0 dan

(1 — θ)> 0.

Untuk

a₂ = μ AB + βμAB + aμAB + μAB² > 0

(μ + β + a + 1XμB) A > 0   (17)

Dari pertidaksamaan (17), jelas (μ + β + a +1),   μ dan   B = (μ + μ_t + β}

bernilai positif. Sehingga diperoleh :

A > 0

a(1 — O')-(μ + μ_t + β) > 0

a(1 - θ)  _>1

^μ + μ_t ^{+ β}

Sedangkan

a(1 — θ) ^{μ +} μ_t ^{+ β})

merupakan R ,

sehingga diperoleh :

R 0 > 1

Maka dapat diperoleh titik tetap endemik penyakit akan stabil asimtotik jika R₀ > 1yang berarti bahwa akan selalu terjadi penyebaran penyakit di dalam populasi yang menyebabkan penyakit akan endemik di suatu daerah. Sedangkan titik tetap endemik penyakit akan tidak stabil jika R₀ < 1yang menunjukkan pada populasi tidak terjadi penyebaran penyakit campak.

• 2.4    Model Dinamika Penyebaran Penyakit Campak dengan Pengaruh Vaksinasi di Provinsi Nusa Tenggara Barat (NTB)

Berdasarkan data dari Badan Pusat Statistika (BPS) Provinsi NTB, pada tahun 2016 jumlah penduduk NTB sebanyak 4.896.162 jiwa. Menurut profil kesehatan NTB tahun 2016, ditemukan kasus campak sebanyak 171 kasus. Jumlah individu yang divaksinasi campak dari anak-anak sebanyak 307.858 anak, sedangkan tidak ada data yang menunjukkan jumlah orang dewasa yang divaksinasi, sehingga pada kasus ini, diasumsikan dimasukkan ke populasi vaksinasi. Oleh karena itu jumlah populasi tervaksinasi adalah 4.700.160 jiwa. Adapun jumlah populasi rentan adalah 195.831 jiwa. Nilai-nilai variabel tersebut akan menjadi nilai awal dari model dinamika penyebaran penyakit campak dengan pengaruh vaksinasi.

Menurut profil kesehatan NTB tahun 2016, jumlah kelahiran (∏) bayi di NTB pada tahun 2016 sebanyak 105.598 bayi. Jadi rata-rata kelahiran bayi perbulan adalah 8.800 bayi, sedangkan cakupan vaksinasi pada bayi (θ) pada tahun tersebut mencapai 99,99%. Pada tahun yang sama, ditemukan kematian akibat campak sebanyak satu orang, sehingga berdasarkan penentuan parameter pada bab sebelumnya didapatkan laju kematian akibat penyakit sebesar μ = jyj = 0.000487 /bulan.       Adapun

berdasarkan data BPS, angka harapan hidup penduduk Provinsi NTB tahun 2016 adalah 65,48 tahun, sehingga laju kematian alami manusia sebesar u. =---------= 0,001273

65,48 ×12

/bulan.

Berdasarkan pada penentuan parameter pada bab sebelumnya, laju kontak = (171 ÷ 12)× 4896162 -------------------= 2,083503/bulan. 171×195831

Lama infeksi penyakit campak berdasarkan tabel (2.1) adalah 17 hari. Adapun menurut Badan Pencegahan dan Pengendalian Penyakit Indonesia (2016), peluang terinfeksinya individu rentan adalah 90%, sehingga laju perpindahan dari populasi rentan ke populasi infeksi atau laju infeksi adalah

α = ²,⁰⁸³⁵⁰3 × 90% = 3,₆7₆402₁ (17 ÷ 30)

/bulan. Laju perpindahan dari populasi infeksi ke populasi tervaksinasi atau laju kesembuhan

adalah β =------= 1,764706/bulan.

17 ÷ 30

Berdasarkan penentuan parameter di atas, maka didapatkan model dinamika penyebaran penyakit campak dengan pengaruh vaksinasi di Provinsi NTB adalah sebagai berikut :

^dS = (8.800) × 0,01% - 3,6764021 SI- - 0,001273S dt                         N

^dI- = 3,6764021 — - 0,0012731 - 0,0004871 -1,7647061 dt           N

dV

— = (8.800) × 99,99% +1,7647061 - 0,001273V dt

• 2.5    Hasil Simulasi Model dengan Matlab

Berdasarkan data dari BPS dan Profil Kesehatan Provinsi NTB, nilai awal yang digunakan pada model ini adalah S(0)  =

• 195.831 , I(0) = 171 dan V(0) = 4.700.160..

waktu sampai 10.000 bulan. Dari gambar 4.2 terlihat adanya perubahan jumlah populasi rentan (S), terinfeksi (I) dan vaksinasi (V) terhadap waktu. Pada waktu kurang dari 1.000 bulan, perubahan ketiga populasi terlihat sangat jelas. Populasi rentan yang semula sebesar 195.831 jiwa, seiring berjalannya waktu mengalami penurunan jumlah, begitu juga dengan populasi infeksi yang semula berjumlah 171 jiwa, jumlahnya semakin menurun. Lain halnya dengan populasi vaksinasi yang awalnya berjumlah 4.700.160 jiwa, seiring berjalannya waktu jumlahnya semakin meningkat. Ketiga populasi tersebut akan terus mengalami perubahan jumlah seiring berjalannya waktu hingga menuju titik tetapnya. Didapatkan dari model dinamika tersebut bilangan reproduksi dasar (R₀) sebesar 0,000208 dan titik tetap model adalah (S,I,V) = ((691,280439), (0), (6.912.113,118617)).Titik tetap yang didapatkan adalah titik tetap bebas penyakit (E₀ ) karena jumlah populasi terinfeksi adalah nol. Titik tetap ini akan stabil karena nilai R₀ < 1. Hal ini menunjukkan tidak ada individu yang terinfeksi yang akan menularkan penyakit campak kepada individu rentan dalam waktu yang tidak terbatas, sehingga pada akhirnya Provinsi NTB bebas dari penyakit campak. Titik tetap dibulatkan menjadi (S,I,V) = ((691), (0), (6.912.113)). Pada saat titik tetap tersebut stabil, maka jumlah individu rentan akan konstan yaitu sebanyak 691 jiwa, jumlah individu terinfeksi adalah nol (tidak ada) dan jumlah individu vaksinasi juga akan konstan adalah 6.912.113 jiwa.

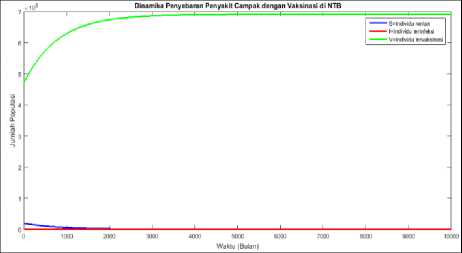
Gambar 4.2. Plot dinamika penyebaran penyakit campak dengan vaksinasi di NTB

Gambar 4.2.    menunjukkan plot

perkembangan penyakit campak di NTB dengan

Adapun plot dari masing-masing populasi dapat dilihat pada gambar 4.3, gambar 4.4, dan gambar 4.5.

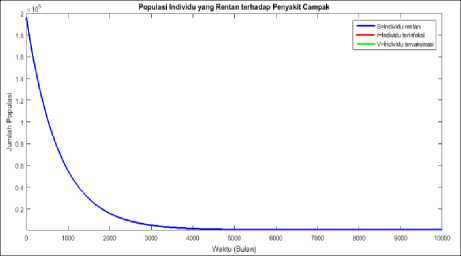
Gambar 4.3. Plot populasi rentan

Gambar 4.4. Plot populasi terinfeksi

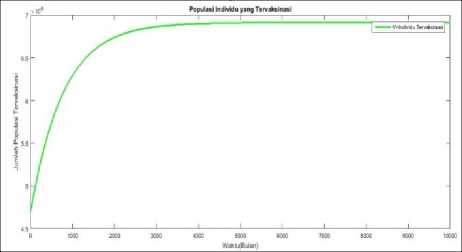
Gambar 4.5. Plot populasi vaksinasi

Pada gambar 4.3, gambar 4.4, dan gambar 4.5, terlihat masing-masing populasi mengalami perubahan seiring berjalannya waktu. Besar kecilnya laju yang masuk pada setiap populasi, dikarenakan laju cakupan vaksinasi yang diberikan pada individu baru. Hal ini menunjukkan, cakupan vaksinasi mempunyai pengaruh terhadap ketiga jumlah populasi.

Untuk mengetahui lebih jelasnya pengaruh vaksinasi terhadap penyebaran penyakit campak, bisa dilihat pada gambar 4.6 dan gambar 4.7. Cakupan vaksinasi campak (θ) yang sudah dilakukan di Provinsi NTB yaitu sebesar 99,99%, dibandingkan dengan cakupan vaksinasi sebesar 50% dan 0%, dengan nilai parameter yang lainnya sama. Didapatkan hasil sebagai berikut :

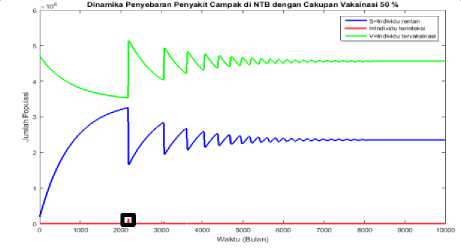
Gambar 4.6. Dinamika penyebaran penyakit campak dengan θ = 50%

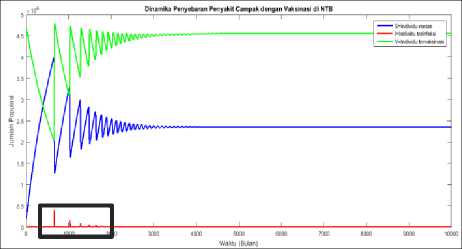
Gambar 4.7. Dinamika penyebaran penyakit campak dengan θ = 0%

Dengan nilai awal yang sama seperti sebelumnya yaitu S(0) = 195.831, I(0) = 171 dan V(0) = 4.700.160 didapatkan plot populasi dengan cakupan vaksinasi 50% dan 0%.

Pada model dinamik penyebaran penyakit campak dengan cakupan vaksinasi 50% didapatkan bilangan reproduksi dasar sebesar 1.040609dan titik tetap model adalah (S,I,V) = ((3.321.517,225762), (97,204579), (3.591.152,782048)).Titik tetap yang didapatkan adalah titik tetap endemik penyakit (E₁ ) karena jumlah populasi terinfeksi tidak sama dengan nol. Titik tetap endemik penyakit akan stabil asimtotik karena nilai R₀ > 1. Hal ini menunjukkan setiap individu yang terinfeksi dapat menularkan penyakit campak kepada lebih dari satu individu rentan, sehinggan menjadi individu terinfeksi baru. Sehingga pada akhirnya terjadi penyebaran penyakit campak yang meluas di Provinsi NTB. Adapun titik tetap endemik penyakit tersebut adalah (S,I,V) = ((3.321.517,225762), (97,204579), (3.591.152)) atau jika dibulatkan menjadi (S,I,V) = ((3.321.517), (97), (3.591.153))., menunjukkan bahwa dalam keadaan stabil, jumlah populasi rentan sebesar 3.321.517 jiwa, populasi terinfeksi sebesar 97 jiwa dan populasi vaksinasi sebesar 3.591.153 jiwa.

Pada model dinamik penyebaran penyakit campak dengan cakupan vaksinasi 0% didapatkan bilangan reproduksi dasar sebesar 2,081219 dan titik tetap model adalah (S,I,V) = ((3.321.517,225762), (2.588,053706), (3.587.709,031488)). Titik tetap yang didapatkan adalah titik tetap endemik penyakit (E₁ ) karena jumlah populasi terinfeksi tidak

sama dengan nol. Titik tetap endemik penyakit akan stabil asimtotik karena nilai R₀ > 1 . Hal ini berarti setiap individu yang terinfeksi dapat menularkan penyakit campak kepada lebih dari satu individu rentan, sehingga menjadi individu terinfeksi baru. Sehingga pada akhirnya terjadi penyebaran penyakit campak yang meluas di Provinsi NTB. Adapun titik tetap endemik penyakit (S,I,V) = ((3.321.517,225762), (2.588,053706), (3.587.709,031488)) atau jika dibulatkan menjadi (S,I,V) = ((3.321.517), (2.588), (3.587.709)), menunjukkan bahwa dalam keadaan stabil, jumlah populasi rentan sebesar 3.321.517 jiwa, populasi terinfeksi sebesar 2.588 jiwa dan populasi vaksinasi sebesar 3.587.709 jiwa.

Kedua hasil tersebut berbeda dengan hasil penyebaran penyakit campak dengan cakupan vaksinasi 99,99%. Pada cakupan vaksinasi 99,99%, titik tetap yang diapatkan adalah titik tetap bebas penyakit, sehingga pada keadaan stabil jumlah populasi infeksi adalah nol. Sekalipun pada cakupan vaksinasi 50% diadakan vaksinasi pada individu baru, namun hal itu tidak mampu mencegah endemiknya penyakit campak. Lain halnya dengan cakupan vaksinasi yang mencapai 99,99%, yang pada akhirnya mampu membuat Provinsi NTB bebas dari penyakit campak. Sana halnya dengan cakupan vaksinasi 0% atau tidak dilakukan vaksinasi sama sekali, didapatkan hasil yang berbeda cukup signfikan dengan cakupan vaksinasi 99,99%. Kedua hal tersebut menunjukkan cakupan vaksinasi mempunyai pengaruh yang signifikan terhadap penyebaran penyakit campak di Provinsi NTB.Semakin besar cakupan vaksinasi di Provinsi NTB, semakin sedikit individu yang rentan pada titik tetapnya dan semakin cepat menghilangnya penyakit campak.

• 3 KESIMPULAN DAN SARAN

• 3.1    Kesimpulan

Berdasarkan penelitian yang telah dilakukan dan analisis data, maka dapat disimpulkan model matematika penyebaran penyakit campak dengan pengaruh vaksinasi yaitu :

^dS =(1-θ)∏-^αSI-µS dt           N

dI  αSI

dt N

_-

µI - µ_t I - βI

^dV =θ∏+βI -µV dt

dengan dua titik tetap model (E0) yaitu titik tetap bebas penyakit dan titik tetap endemik penyakit (E 1). E₀akan stabil jika jumlah rata-rata individu rentan yang terinfeksi kurang dari satu, sedangkanE ₁akan stabil jika rata-rata individu rentan yang terinfeksi lebih dari satu.

Titik tetap yang didapatkan dari model dinamika penyebaran penyakit campak dengan pengaruh vaksinasi di Provinsi Nusa Tenggara Barat adalah (S,I,V) = ((691,280439), (0), (6.912.113,118617)), dengan jumlah rata-rata individu rentan yang terinfeksi adalah 0,000208. Titik tetap yang didapatkan adalah stabil asimtotik, yang berarti jika parameter-parameternya tidak berubah maka penyakit campak akan menghilang di NTB. Berdasarkan simulasi juga didapatkan semakin besar cakupan vaksinasi yang dilakukan di Provinsi NTB maka semakin sedikit individu yang rentan saat keadaan stabil dan semakin cepat menghilangnya penyakit campak.

• 3.2    Saran

Pada penelitian ini, tidak memperhatikan migrasi, pencegahan dengan vaksin dan tanpa adanya pengobatan. Untuk peneliti selanjutnya yang tertarik dengan model matematika campak ini, diharapkan dapat melibatkan migrasi, pencegahan dengan selain vaksin dan dengan pengobatan.

DAFTAR PUSTAKA

Aziziah, A.N., 2017, Model Sir pada Epidemi Penyakit Campak Berdasarkan Umur dengan Pengaruh Vaksinasi, MATH-unesa Jurnal Ilmiah Matematika, Vol. 3, No.4.

Boyce, W. E. dan Diprima, R.C.,  2012,

Elementary Differential Equation and BoundaryValue Problems Tenth Edition, John Wiley & Sons, Inc.,United State of America.

BPS Provinsi NTB, 2017, NTB dalam Angka tahun 2016, BPS NTB, Mataram.

Cherry, J.D., Harrison, G.D., Kaplan, S., Hotez, P., dan Steinbach, W., 2014, Textbook of Pediatric Infectious Diseases : Measles Virus, Elsevier Inc, Philadelphia.

Chin, J., 2000, Manual Pemberantasan Penyakit MenularEdisi 17 Cetakan IV Terjemahan Dr. I Nyoman Kandun, Mph Edisi ke-17, Bakti Husada, Jakarta.

Depkes RI, 2017, Petunjuk Teknis Kampanye Imunisasi                       Measles-

Rubella,(http://www.depkes.go.id), diakses jam 10.00 WITA, tanggal 25 Januari 2018.

Depkes RI, 2008, Profil Pengendalian Penyakit dan Penyehatan Lingkungan Tahun 2009, Jakarta.

Diekmann, O., dan Heesterbeek, J.A.P., 2000, Mathematical Epidemiology of Infectious Diseases: Model Building, Analiysis and Interpretation, John Wiley & Sons, Inc., United State of America.

Dinas Kesehatan Provinsi NTB, 2015, Profil Kesehatan Provinsi Nusa Tenggara Barat tahun 2015, Dikes NTB, Mataram.

Dinas Kesehatan Provinsi NTB, 2016, Profil Kesehatan Provinsi Nusa Tenggara Barat tahun 2016, Dikes NTB, Mataram.

Direktorat Jenderal Pencegahan dan Pengendalian Penyakit Indonesia, 2017, Petunjuk Teknis Kampanye Imunisasi Measles-Rubella,(http://www.depkes.go.id), diakses jam 10.00 WITA, tanggal 25 Januari 2018.

Driessche, V.D.P. dan Watmough, J., 2002,

Reproduction Numbers and Subthreshold Endemic Equilibria for Compartmental Models of Disease Transmission, Journal of Mathematical Biosciences, 180, pp. 29-48.

Haffernan, J.M. dan Kelling, M.J., 2007, An inhost model of acute infection: Measles as a case study, Theoretical Population Biology, 73, 134–147.

Hethcote, H.W., 2000, The Mathematics of

Infectious Diseases, SIAM Review, Vol. 42, No. 4, pp. 599-653.

Lashari, A.A., 2016, Optimal Control of an SIR Epidemic Model with a Saturated Treatment, Appl. Math. Inf. Sci., 10, No. 1, 185-191.

Mantra, I.B., 2006, Demografi Umum, Pustaka Pelajar ,Yogyakarta.

Ngilawajan, D.A., 2010, Model Matematika

untuk Penangkapan Ikan Pada Budidaya Ikan, Buletin Pendidikan Matematika, Vol. 10, No. 1, pp 81-90.

Perko, L., 2001, Differential Equations and

Dynamical Systems Third Edition, Springer, New York.

Verguet, S., Jones, J.E.O., Johri, M., Morris, S.K., Suraweera, W., Cindy L., dan Gauvreau, 2017, Characterizing Measles Transmission in India: A Dynamic Modeling Study using Verbal Autopsy Data, BMC Medicine (2017) 15:151.

WHO, 2004, Treating Measles in Children, (www.who.int/immunization) diunduh jam 10.45 WITA, tanggal 25/01/2018.

121