ANALISIS SINTASAN PARAMETRIK PADA PASIEN STROKE DENGAN PENDEKATAN DISTRIBUSI WEIBULL
on
E-Jurnal Matematika Vol. 8(1), Januari 2019, pp. 55-63
DOI: https://doi.org/10.24843/MTK.2019.v08.i01.p235
ISSN: 2303-1751
ANALISIS SINTASAN PARAMETRIK PADA PASIEN STROKE DENGAN PENDEKATAN DISTRIBUSI WEIBULL
Ni Made Sri Wahyuni1§, I Wayan Sumarjaya2Ni Luh Putu Suciptawati3
1Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: madesri80@gmail.com]
2Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: sumarjaya@unud.ac.id]
3Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: suciptawati@unud.ac.id]
§Corresponding Author
ABSTRACT
Parametric survival analysis is one of the survival analysis that has a distribution of survival data that follows a certain distribution. Weibull distribution is a distribution that is often used in parametric survival analysis. The purpose of this study is to determine parametric survival models using the Weibull distribution and to determine the factors that can influence the recovery of stroke patients. This study uses data on stroke patients in the Wangaya hospital, Denpasar in 2017. The best model obtained in this study is a model that consists of two predictor variables, namely the age and the body mass index (BMI).Therefore the factors that can influence the recovery of stroke patients are age and BMI.
Keywords: Parametric survival analysis, stroke, Weibull.
Stroke merupakan penyakit yang terjadi pada otak yang menyebabkan gangguan fungsi saraf lokal atau global dengan kemunculan yang mendadak, progresif, dan cepat (Kemenkes, 2013). Menurut WHO (2016) secara global stroke merupakan penyebab kematian kedua dan penyebab keenam dari kecacatan.
Jumlah kasus stroke di Indonesia berdasarkan diagnosis kesehatan sebesar 7 kasus per mil dan yang terdiagnosis tenaga kesehatan atau gejala sebesar 12,1 kasus per mil. Jumlah kasus stroke di Bali berdasarkan diagnosis tenaga kesehatan yaitu sebesar 5,3‰ dan berdasarkan terdiagnosis tenaga kesehatan dan gejala yaitu sebesar 8,9‰ (Kemenkes, 2013).
Faktor-faktor yang memengaruhi stroke dapat dikategorikan menjadi dua yaitu faktor risiko yang tidak dapat diubah dan faktor risiko yang dapat diubah. Faktor risiko yang tidak dapat diubah yaitu usia, jenis kelamin, ras atau bangsa, serta faktor riwayat stroke yang diturunkan dari keluarga. Sedangkan faktor risiko yang dapat diubah yaitu seperti hipertensi,
diabetes melitus, penyakit jantung, TIA (transient ischaemic attack), obesitas, kebiasaan merokok, alkohol, stres, penyalahgunaan obat, dan lain-lain.
Penelitian tentang penyakit stroke telah dilakukan oleh beberapa peneliti diantaranya penelitian yang dilakukan oleh Ghani, dkk. (2016) mengenai faktor risiko dominan penderita stroke di Indonesia dan penelitian yang dilakukan oleh Wulandari (2011) yang menerapkan metode least absolute shrinkage (LASSO).
Salah satu analisis yang dapat digunakan untuk menduga faktor-faktor yang memengaruhi kesembuhan pasien penyakit stroke adalah analisis sintasan. Analisis sintasan merupakan salah satu metode statistika yang digunakan untuk menganalisis data, di mana variabel yang diperhatikan adalah waktu sampai dengan terjadinya suatu peristiwa tertentu (Kleinbaum & Klein, 2005).
Analisis sintasan parametrik adalah salah satu analisis sintasan yang memiliki sebaran data waktu sintasan dengan mengikuti suatu
distribusi tertentu seperti distribusi Weibull, eksponensial, log-logistik, lognormal, dan generalisasi gamma (Kleinbaum & Klein, 2005). Dalam analisis sintasan parametrik estimasi yang diperoleh dari model menghasilkan plot yang lebih konsisten. Selain itu, parameter dapat ditentukan menggunakan distribusi yang mendasari, sehingga fungsi sintasan dan fungsi hazard dapat ditentukan. Kesederhanaan dan kelengkapan inilah yang membuat analisis sintasan parametrik menarik untuk digunakan.
Penelitian tentang analisis sintasan parametrik telah dilakukan oleh beberapa peneliti. Bastyan & Latra (2013) melakukan penelitian tentang analisis sintasan dengan model regresi Cox Weibull pada penderita demam berdarah dengue (DBD) di rumah sakit Haji Sukolilo Surabaya. Yogesswara dkk. (2018) melakukan penelitian tentang estimasi sintasan penderita diabetes melitus dengan komparasi kinerja regresi PLS dan LASSO. Selain itu, Monica & Purhadi (2016) melakukan penelitian mengenai analisis faktor yang memengaruhi laju kesembuhan pasien tuberkulosis paru di RSUD Dr. Soetomo tahun 2015 menggunakan regresi Weibull dan regresi Cox Proportional Hazard.
Tujuan dari penelitian ini adalah untuk mengetahui model sintasan parametric dengan pendekatan distribusi Weibull dan untuk mengetahui faktor-faktor yang memengaruhi kesembuhan pasien penyakit stroke.
Menurut Kleinbaum & Klein (2005) di dalam analisis sintasan terdapat data tersensor yang harus diperhatikan. Penyebab munculnya data tersensor yaitu:
-
1. Individu tidak mengalami kejadian hingga penelitian berakhir.
-
2. Individu hilang dari penelitian dalam periode penelitian.
-
3. Individu mengeluarkan diri dari penelitian karena kematian (jika kematian bukan kejadian yang diperhatikan) atau karena suatu alasan tertentu.
Distribusi waktu dalam analisis sintasan dapat dijelaskan dengan tiga fungsi yaitu fungsi sintasan (survivorship function), fungsi densitas probabilitas (probability density function), dan fungsi hazard (hazard function). Ketiga fungsi
tersebut memiliki keterkaitan satu sama lain. Jika salah satu fungsi sudah diketahui maka kedua fungsi lainnya akan dapat dicari.
-
1. Fungsi Sintasan
-
2. Fungsi Densitas Probabilitas
f(t)=
P[seorang individu mati dalam interval (t,t+Δt)] limΔt→O ----------------------1
(2)
-
3. Fungsi Hazard
Model regresi Cox merupakan model yang paling populer digunakan dalam analisis sintasan karena rasio hazard bisa ditentukan tanpa mengetahui baseline hazard, estimasi koefisien regresinya baik, kurva sintasan dapat diperoleh untuk berbagai macam data (Kleinbaum & Klein, 2005). Persamaan model untuk Cox proportional hazard yaitu:
ℎ(t, *)=ℎO(t) ехр(∑i=ι βixi). (4)
dengan ℎo(t) adalah baseline hazard yang tidak perlu diketahui, xi adalah peubah-peubah bebas terdiri dari xι , X2 , X3,…,Xp , dan βi adalah
parameter dari peubah-peubah bebas terdiri dari βι , β2 , β3,…,βp .
Analisis sintasan parametrik adalah salah satu analisis sintasan yang mana sebaran data waktu sintasannya mengikuti suatu distribusi tertentu. Contoh dari distribusi yang umum digunakan untuk analisis sintasan parametrik adalah Weibull, eksponensial (kasus khusus dari Weibull), log-logistik, lognormal, dan generalisasi gamma (Kleinbaum & Klein, 2005).
Model distribusi Weibull adalah model sintasan yang paling banyak digunakan. Bentuk umum fungsi hazard dari distribusi Weibull diberikan sebagai berikut (Kleinbaum & Klein, 2005).
Fungsi sintasan pada distribusi Weibull yaitu:
Fungsi densitas peluang distribusi hazard yaitu:
DOI: https://doi.org/10.24843/MTK.2019.v08.i01.p235
Menurut Collet (1994) model proportional hazard distribusi Weibull dapat dinyatakan sebagai berikut:
ℎi(t) = ехр(β′X)ℎO(t). (8)
dengan ℎQ(t)= λptp 1 adalah baseline hazard yang dispesifikasikan pada parameternya dalam hal ini adalah distribusi Weibull.
Data yang diperoleh terdiri atas n pengamatan waktu sintasan, ditunjukkan oleh tI , ^2 ,...,tn ; ^i adalah indikator sensor yang bernilai nol bila tersensor kanan untuk waktu sintasan ke-i, ⅛ (1,2,3,...,n) dan bernilai satu untuk yang lainnya. Maka fungsi likelihood dapat dinyatakan dalam bentuk:
L(β)= ∏ {h(⅛)}5{St (ti)}I-S . (9) dengan fi ( ti ) adalah fungsi densitas dan Si (ti) adalah fungsi sintasan.
Peubah yang berpengaruh terhadap model didapatkan melalui uji signifikansi parameter. Berikut ini pengujian parameter yang dilakukan setelah mendapatkan model (Lee, 1997).
Hipotesis:
H0 ∶ = 0, i = 1,2,3,...,P;
Hi ∶ ≠0,i = 1,2,3,...,P.
Statistik Uji:
Uji Wald yang berbentuk:
̂
‰ = ( ̂;).
Daerah kritis : Hipotesis nol (H0) tidak diterima jika Xhitung > Xl ,a atau jika P-value < a.
Jenis data yang digunakan pada penelitian ini adalah berupa data sekunder. Data sekunder yang digunakan dalam penelitian ini adalah data yang sebelumnya telah dikumpulkan oleh Rumah Sakit Wangaya yang berupa data hasil rekam medis pasien penderita penyakit stroke yang dirawat inap pada tahun 2017.
Variabel respons yang digunakan pada penelitian ini adalah lama pasien penyakit stroke dirawat inap di Rumah Sakit Umum Daerah Wangaya, Denpasar tahun 2017. Variabel prediktor yang digunakan pada penelitian ini adalah usia (X1), jenis Kelamin (X2), jenis stroke (X3), hipertensi (X4), penyakit jantung (X5), diabetes melitu (X6), dan indeks massa tubuh (IMT) (X7).
Adapun langkah-langkah analisis yang akan dilakukan dalam penelitian ini yaitu:
-
1. Melakukan analisis deskriptif untuk melihat karakteristik dari pasien penyakit stroke yang dirawat inap di RSUD Wangaya tahun 2017.
-
2. Menguji asumsi proportional hazard menggunakan plot log minus log atau log(-log(S(t)) terhadap waktu sintasan untuk setiap variabel prediktor.
-
3. Melakukan pengujian distribusi Weibull pada variabel respons menggunakan uji Anderson-Darling.
-
4. Menyusun model proportional hazard
Weibull.
-
5. Melakukan seleksi model terbaik dengan metode backward elimination serta melihat perubahan -2 log likelihood pada model yang dihasilkan dari pendekatan distribusi Weibull.
-
6. Melakukan pengujian secara parsial melalui pendekatan distribusi Weibull untuk mengetahui peranan masing-masing variabel prediktor terhadap variabel respons.
-
7. Mendapatkan model proportional hazard Weibull.
-
8. Interpretasi model proportional hazard Weibull.
Analisis deskriptif digunakan untuk menunjukkan karakteristik ataupun gambaran umum dari data yang telah diperoleh yaitu berupa data hasil rekam medis pasien stroke yang dirawat inap di Rumah Sakit Umum
Daerah Wangaya Denpasar pada tahun 2017. Data yang digunakan dalam penelitian ini adalah sebanyak 100 data pasien stroke.
Persentase jumlah pasien stroke berdasarkan usia yaitu diperoleh persentase tertinggi pada usia 55─64 tahun dan 65─74 tahun dengan masing-masing persentase yaitu sebesar 26%. Peningkatan usia berhubungan dengan proses penuaan yaitu semua organ tubuh mengalami kemunduran fungsi termasuk pembuluh darah otak (Kristyawati, dkk., 2009). Julmah pasien stroke berjenis kelamin laki-laki pada penelitian ini memiliki persentase yang lebih banyak yaitu sebesar 53%, sedangkan jenis kelamin perempuan memiliki persentase sebesar 47%. Menurut Krityawati, dkk. (2009) kondisi ini berhubungan dengan gaya hidup laki-laki seperti merokok dan konsumsi alcohol. Jenis stroke non hemoragik merupakan jenis stroke yang paling banyak terjadi yaitu sebesar 84%. Hal tersebut sesuai dengan penelitian Dinata, dkk. (2013) yang memperoleh hasil bahwa jenis stroke non hemoragik lebih besar jumlahnya dibandingkan dengan jenis stroke non hemoragik.
Persentase jumlah pasien stroke berdasarkan hipertensi yaitu sebesar 62% pasien mengalami hipertensi. Menurut Khairatunnisa & Sari (2017) efek jangka panjang dari hipertensi adalah kerusakan dinding arteri dan memudahkan pecahnya pembuluh darah. Pada penelitian ini persentase pasien dengan riwayat penyakit jantung hanya sebesar 10%. Hal ini sesuai dengan penelitian yang dilakukan Kristiyawati, dkk (2009) yang memperoleh hasil bahwa pasien yang menderita penyakit jantung lebih sedikit dibandingkan dengan pasien yang tidak menderita penyakit jantung.
Selanjutnya persentase pasien yang memiliki riwayat diabetes mellitus yaitu sebesar 16%. Hasil penelitian ini bertentangan dengan Udani (2013), selain itu, menurut Ramadany, dkk. (2013) terdapat hubungan diabetes mellitus dengan kejadian stroke iskemik di mana kadar glukosa darah yang berlebih akan mengganggu
elastisitas pembuluh darah. Sebagian besar pasien pada penelitian ini yaitu sebesar 53% memiliki indeks massa tubuh 18,5─24,9 kg/m2. Menurut PERDOSSI (2011), obesitas merupakan salah satu faktor yang dapat mempermudah terjadinya penyakit stroke. Penelitian ini terdapat sebesar 21% pasien yang memiliki status gizi yang berlebih atau obesitas.
Pengujian asumsi proportional hazard setiap variabel prediktor terhadap waktu sintasan dapat dilakukan dengan plot log minus log (LML). Variabel prediktor yang memberikan hasil plot LML yang sejajar dikatakan memenuhi asumsi proportional hazard dan dapat digunakan dalam model proportional hazard Weibull. Gambar 1 menunjukkan bahwa ketujuh variabel prediktor yang digunakan dalam penelitian ini proporsional sehingga dapat digunakan dalam model proportional hazard Weibull.
Uji distribusi dilakukan untuk mengetahui distribusi data variabel respons (waktu sintasan). Pengujian distribusi dapat menggunakan uji distribusi Anderson-Darling. Berdasarkan Gambar 2 dapat dilihat bahwa nilai P-value > 0,05, hal ini berarti waktu sintasan pasien stroke berdistribusi Weibul.
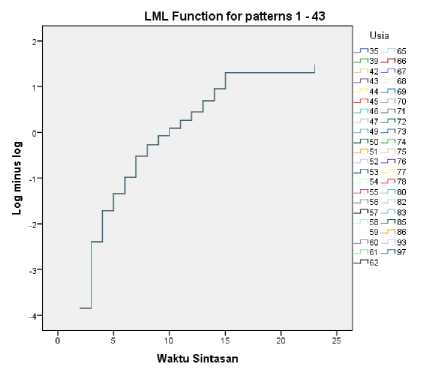
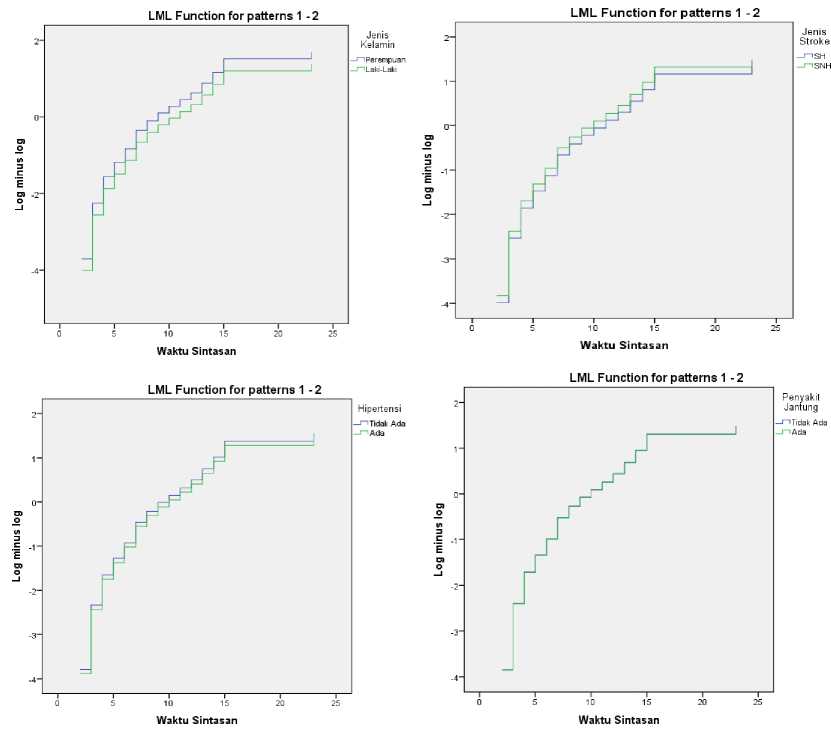
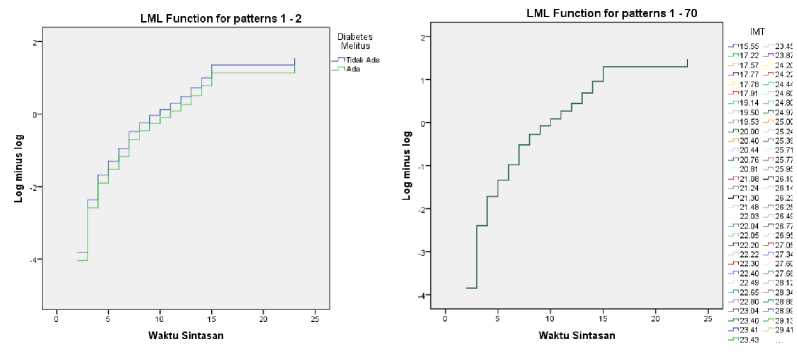
Gambar 1. Plot LML Waktu Sintasan Terhadap Ketujuh Variabel.
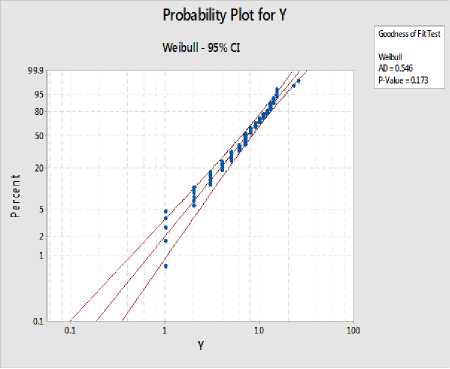
Gambar 2. Plot Distribusi Waktu Sintasan
|
3.4 Menentukan Model Proportional Hazard Weibull |
-intеrcерt λ=ехр[ р ] еrror variancе |
|
Analisis sintasan parametrik memiliki baseline hazard yang harus ditentukan. Baseline hazard atau ℎ0(t) merupakan fungsi hazard untuk individu dengan nilai kovariatnya adalah |
-(-2,767534) =ехр[ 0,4125289 ] 2,767534 =ехр[0,4125289] = ехр[6,70870332] = 819,507311. |
nol. Berdasarkan Tabel 1 dapat diperoleh baseline hazard dalam model proportional hazard Weibull pada pasien stroke adalah sebagai berikut:
Tabel 1. Hasil Analisis Model Proportional Hazard Weibull
|
Variabel |
Koefisien |
Std. error |
Z |
P>|z| |
[95% Conf. Interval] | |
|
X1 |
-0,0215857 |
0,0091826 |
-2,35 |
0,019 |
-0,0395832 |
-0,0035882 |
|
X2 |
-0,259631 |
0,2402777 |
-1,07 |
0,287 |
-0,7268988 |
0,2149726 |
|
X3 |
0,478261 |
0,3974348 |
1,20 |
0,229 |
-0,3006968 |
1,257219 |
|
X4 |
-0,0062832 |
0,2432546 |
-0,03 |
0,979 |
-0, 4830535 |
0,4704872 |
|
X5 |
-0,0741228 |
0,3772851 |
-0,20 |
0,844 |
-0,8135881 |
0,6653424 |
|
X6 |
-0,306554 |
0,3139762 |
-0,98 |
0,329 |
-0.921936 |
0,3088281 |
|
X7 |
-0,0683181 |
0,0304425 |
-2,24 |
0,025 |
-0,1279843 |
-0,0086519 |
|
Konstanta |
-2,767534 |
0,8966259 |
-3,09 |
0,002 |
-4,524889 |
-1,01018 |
|
ln(p) |
0,885449 |
0,083253 |
10,64 |
0,000 |
0,7222762 |
1,048622 |
|
p |
2,424073 |
0,2018112 |
2,059115 |
2,853715 | ||
|
1/p |
0,4125289 |
0,0343443 |
0,3504204 |
0,486456 | ||
Sumber: Data Diolah, 2018
Sehingga baseline hazardnya menjadi:
ℎO(t)=Ap tp 1
= (819,507311)(2,424073)t2, 424073-1
= 1986,54555t1, 424073 .
Langkah selanjutnya adalah menentukan model proportional hazard Weibull. Berdasarkan Tabel 1, dengan menganggap semua variabel berpengaruh maka model proportional hazard Weibull pada pasien stroke adalah sebagai berikut:
ℎi(t) =ехр(βlXl + β2x2 + β3x3 + β4x4
+ β3x3 + β6X6 + β7X7)ℎ0(t)
= ехр(-0,0215857*1 - 0,259631X2 + 0,4782612X3 - 0,0062832X4 -
0,0741228X5 - 0,306554Xe -0,0683181X7) × 1986,54555t1, 424073 .
Langkah selanjutnya adalah menentukan model terbaik dengan dengan menggunakan metode backward elimination. Berikut ini adalah hasil dari backward elimination menggunakan software STATA.
Tabel 2. Hasil Backward Elimination
|
Variabel |
Koefisien |
Std. error |
Z |
P>|z| |
[95% Conf. Interval] | |
|
X1 |
-0,0195386 |
0,0092673 |
-2,11 |
0,035 |
-0,03770 |
-0,001751 |
|
X7 |
-0,0720804 |
0,0268676 |
-2,68 |
0,007 |
-0,12474 |
-0,0194208 |
|
Konstanta |
-2,45037 |
0,898574 |
-2,73 |
0,006 |
-4,211511 |
-0,6892303 |
|
ln(p) |
0,8598117 |
0,082025 |
10,48 |
0,000 |
0,6990454 |
1,020578 |
|
p |
2,362716 |
0,1938021 |
2,011831 |
2,774798 | ||
|
1/p |
0,4232418 |
0,0347165 |
0,3603866 |
0,4970596 | ||
Sumber: Data Diolah, 2018
Berdasarkan Tabel 2 diperoleh model terbaik proportional hazard Weibull yaitu
model yang terdiri dari variabel prediktor X1 dan X7. Sehingga dapat ditentukan baseline hazard
dari model terbaik proportional hazard Weibull
adalah sebagai berikut:
|
-intеrcерt [еrror variancе] | |
|
A=ехр | |
|
-(-2,45037) [ 0,4232418 ] | |
|
=ехр | |
|
2,45037 [0,4232418] | |
|
=ехр |
= ехр[5,7895274] = 326,858515.
Sehingga baseline hazardnya menjadi: ℎO(t) = Aptp 1
= (326,858515)(2,362716)t2, 362716-1 = 772,273842t1, 362716 .
Dengan demikian model terbaik proportional hazard Weibull pasien stroke adalah sebagai berikut:
ℎ i (t) = ехр(-0,0195*1 - 0,0721*7)× 772,2738t1, 362716 .
dengan ^l menyatakan usia dan X7 menyatakan indeks massa tubuh (IMT).
Langkah selanjutnya adalah melakukan uji rasio likelihood yang bertujuan untuk melihat pengaruh variabel-variabel prediktor secara simultan dan menentukan kepentingan relatif dari masing-masing variabel prediktor.
Berdasarkan pada Tabel 3 dapat dilihat bahwa nilai perubahan -2 log yang digunakan dalam menentukan model terbaik adalah 11,019758 atau model terbaik yang digunakan adalah model yang terdiri dari variabel
prediktor X1 dan X7.
Tabel 3. Hasil Analisis Pengujian Rasio Likelihood dengan Pendekatan Distribusi Weibull
|
Model dengan perubahan yang disertakan |
-2log likelihood |
Perubahan |
|
Tanpa variabel prediktor |
139,27991 | |
|
X1 |
135,535306 |
3,744604 |
|
X2 |
137,746492 |
1,533428 |
|
X3 |
139,25498 |
0,02493 |
|
X4 |
138,387126 |
0,892784 |
|
X5 |
139,202652 |
0,077258 |
|
X6 |
137,164582 |
2,115328 |
|
X7 |
132,840984 |
6,438926 |
|
X1+ X7 |
128,260152 |
11,019758 |
|
X1 + X2 |
132,583048 |
6,696862 |
|
X2+ X7 |
132,272656 |
7,007254 |
|
X1 + X3 |
135,49986 |
3,78005 |
|
X3 + X7 |
131,966872 |
7,313038 |
Sumber: Data Diolah, 2018
Langkah selanjutnya adalah melihat ada tidaknya pengaruh nyata variabel prediktor terhadap variabel respons (waktu sintasan) dengan melakukan pengujian secara parsial terhadap masing-masing variabel prediktor.
Berdasarkan hasil pengujian secara parsial data waktu sintasan stroke dengan pendekatan distribusi Weibull yang diperoleh pada Tabel 4, dapat ditunjukkan bahwa variabel yang berpengaruh nyata adalah variabel X1 dan X7 dengan nilai p-value < 0,05 yaitu masing-masing sebesar 0,019 dan 0,025.
Tabel 4. Hasil Uji Parsial Data Waktu Sintasan Pasien Stroke dengan Pendekatan Distribusi Weibull
|
Variabel Prediktor |
̂ |
P-value |
Keputusan |
|
X1 |
-0,0215857 |
0,019 |
Tolak H0 |
|
X2 |
-0,259631 |
0,287 |
Terima Hq ∖ |
|
X3 |
0,478261 |
0,229 |
Terima Hq ∖ |
|
X4 |
-0,0062832 |
0,979 |
Terima Hq ∖ |
|
X5 |
-0,0741228 |
0,844 |
Terima Hq ∖ |
|
X6 |
-0,306554 |
0,329 |
Terima Hq ∖ |
|
X7 |
-0,0683181 |
0,025 |
Tolak H0 |
Sumber: Data Diolah, 2018
-
3.5 Menentukan Hazard Ratio Model
Proportional Hazard Weibull
Hazard ratio dapat digunakan untuk menginterpretasikan koefisien dari variabel prediktor pada model proportional hazard Weibull. Faktor-faktor yang memengaruhi kesembuhan pasien stroke dapat dilihat dari nilai hazard ratio variabel yang berpengaruh secara signifikan.
Berdasarkan Tabel 5 dapat dilihat bahwa nilai hazard ratio untuk variabel X1 sebesar 0,980651, hal ini berarti bahwa untuk peningkatan satu unit pada kovariat usia akan mengurangi risiko kesembuhan sebesar 1,9%. Sedangkan variabel X7 memiliki nilai hazard ratio sebesar 0,9304561, hal ini berarti bahwa untuk peningkatan satu unit pada kovariat IMT akan mengurangi risiko kesembuhan sebesar 6,9%.
Berdasarkan hasil dan pembahasan pada penelitian ini, dari ketujuh variabel prediktor yang digunakan untuk memodelkan kesembuhan pada pasien penyakit stroke hanya terdapat dua variabel prediktor yang berpengaruh nyata terhadap kesembuhan pasien yaitu usia dan indeks massa tubuh (IMT).
Adapun saran yang bisa diberikan untuk penelitian selanjutnya adalah Pada penelitian selanjutnya dapat menambahkan variabel prediktor lain yang memengaruhi kesembuhan pasien stroke dan kelengkapan informasi pada data yang diperoleh lebih diperhatikan.
Tabel 5. Hasil Analisis Hazard Ratio Model Proportional Hazard Weibull
|
Variabel |
Hazard Ratio |
Std. error |
Z |
P>|z| |
[95% Conf. Interval] | |
|
X1 |
0,980651 |
0,009088 |
-2,11 |
0,035 |
0,9629998 |
0,9986259 |
|
X7 |
0,9304561 |
0,249992 |
-2,68 |
0.007 |
0,8827264 |
0,9807666 |
|
ln(p) |
0,8598117 |
0, 0820251 |
-2,73 |
0,006 |
0,6990454 |
1,020578 |
|
P |
2,362716 |
0,1938021 |
10,48 |
2,011831 |
2,774798 | |
|
1/p |
0,4232418 |
0,0347165 |
0,3603866 |
0,4970596 | ||
Sumber: Data Diolah, 2018
DAFTAR PUSTAKA
Bastyan, E., & Latra, I. N. (2013). Analisis Survival dengan Model Regresi Cox Weibull pada Penderita Demam Berdarah Dengue (DBD) di Rumah Sakit Haji Sukolilo Surabaya. Jurnal Sains dan Seni Pomits Vol. 2, No. 2, 2337-3520.
Collet, D. (1994). Modeling Survival Data in Medical Research. London : Chapman and Hall. Cox, D. (1972). Regression Models and Life -Tables. Journal of The Royal Statistical Society. Series B
(Methodological), Vol. 34, No. 2 , 187220.
Dinata, A. C., Safrita, Y., & Sastri, S. (2013). Gambaran Faktor Risiko dan Tipe Stroke pada Pasien Rawat Inap di Bagian Penyakit Dalam RSUD Kabupaten Solok Selatan Periode 1 Januari 2010-3 Juni 2012. Jurnal Kesehatan Andalas,Vol.2, No. 2, 57-61.
Ghani, L., Mihardja, L. K., & Delima. (2016). Faktor Risiko Dominan Penderita Stroke di Indonesia. Buletin Penelitian Kesehatan, Vol. 44, No. 1, 49-58.
Kemenkes. (2013). Riset Kesehatan Dasar. Jakarta: Badan Penelitian dan
Pengembangan Kesehatan Kementerian Kesehatan RI.
Khairatunnisa, & Sari, D. M. (2017). Faktor Risiko yang Berhubungan dengan Kejadian Stroke pada Pasien di RSU H. Sahudin Kutacane Kabupaten Aceh Tenggara. Jurnal Jumantik, Vol.2, No.1, 60-70.
Kleinbaum, D. G., & Klein, M. (2005).
Survival Analysis A Self-Learning Text. New York: Spinger Science+Business Media, Inc.
Kristiyawati, S. P., Irawaty, D., & Hariyati, R.
T. (2009). Faktor Risiko Yang Berhubungan Dengan Kejadian Stroke Di Rumah Sakit Panti Wilasa Citarum Semarang . J. Keperawatan dan Kebidanan (JIKK), Vol. 1 No. 1, 1-7.
Le, C. T. (1997). Applied Survival Analysis. New York: John Wiley & Sons, Inc.
Monica, Y. S. A., & Purhadi. (2016). Analisis Faktor yang Memengaruhi Laju Kesembuhan Pasien Tuberkulosis Paru di RSUD Dr. Soetomo Tahun 2015 Menggunakan Regresi Weibull dan Regresi Cox Proportional Hazard. Jurnal Sains dan Seni ITS, Vol. 5, No. 2, 23373520.
PERDOSSI. (2011). Guideline Stroke. Jakarta: Perhimpunanan Dokter Spesialis Saraf Indonesia (PERDOSSI).
Ramadany, A. F., Pujarini, L. A., &
Candrasari, A. (2013). Hubungan Diabetes Melitus dengan Kejadian Stroke Iskemik di RSUD dr. Moewardi Surakarta Tahun 2010. Biomedika, Vo. 5 No. 2, 11-16.
Udani, G. (2013). Faktor Resiko Stroke. Jurnal Kesehatan Metro Sai Wawai, Vol.6, No.1, 49-57.
WHO. (2016). Tobacco & Stroke. Switzerland: WHO Document
Production.http://www.wpro.who.int/ch ina/topics/tobacco/tbs-2016-en.pdf.
Wulandari, P. R., (2011)."Penerapan Metode Regresi Least Absolute Shrinkage and Selection Operator (LASSO) Terhadap Waktu Tahan Hidup Penderita Stroke". Skripsi. Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Udayana.
Yogesswara, G. A., Kencana, E. N., &
Sukarsa, I. K. (2018). Estimasi Sintasan Penderita Diabetes Melitus: Komparasi Kinerja Regresi PLS dan LASSO. E-Jurnal Matematika Vol. 7, No.4, 339-345.
63
Discussion and feedback