PETA KENDALI EWMA RESIDUAL PADA DATA BERAUTOKORELASI

E-Jurnal Matematika Vol. 8(1), Januari 2019, pp.64-73

DOI: https://doi.org/10.24843/MTK.2019.v08.i01.p236

ISSN: 2303-1751

PETA KENDALI EWMA RESIDUAL PADA DATA BERAUTOKORELASI

Ni Kadek Yuni Dewiantari^1§, I Wayan Sumarjaya ², G.K. Gandhiadi³

• ¹Program Studi Matematika, Fakultas MIPA - Universitas Udayana [Email: kadekyuni48@gmail.com]

• ²Program Studi Matematika, Fakultas MIPA - Universitas Udayana [Email: sumarjaya@unud.ac.id]

• ³Program Studi Matematika, Fakultas MIPA - Universitas Udayana [Email: gandhiadi@unud.ac.id]

^§Corresponding Author

ABSTRACT

Control charts with autocorrelation can be overcome by creating control chart with residuals from the best forecasting model. EWMA control chart is a alternative to the Shewhart control chart when detecting small shifts. The purpose of this study is to make the best forecasting model to obtain residual, and see the stability of the rupiah exchange rate against US dollar using EWMA control chart with residual. The best model of the case is ARIMA (1,1,1). The results of the EWMA residual control chart with λ = 0.1 there is a pattern that makes the process unstable.

Keywords: Control Chart, EWMA, Time Series, Rupiah Exchange Rate

• 1.    PENDAHULUAN

Produk dan jasa yang berkualitas baik adalah produk dan jasa yang sesuai dengan keinginan konsumen (Ariani, 2004). Peningkatan kualitas adalah pengurangan variabilitas (kesalahan) dalam proses dan produk. Hal ini menyiratkan bahwa jika variabilitas yang terjadi menurun, maka kualitas produk meningkat (Montgomery, 2005).

Pengendalian kualitas tidak hanya diaplikasikan pada bidang industri, namun juga bidang lain seperti bidang kimia, farmasi, dan keuangan. Sebagai contoh dalam bidang keuangan yaitu pengendalian nilai tukar rupiah terhadap dolar Amerika Serikat (USD). Menurut Bank Indonesia (2017) kestabilan nilai tukar rupiah terhadap mata uang asing berpengaruh terhadap perekonomian di Indonesia. Melemahnya nilai tukar rupiah terhadap dolar dapat menimbulkan beberapa hal antara lain: meningkatnya nilai suku bunga yang berdampak pada perubahan investasi di Indonesia, terjadinya inflasi yang menyebabkan harga-harga meningkat secara umum, dan permasalahan ekonomi lainnya. Melihat dampak dari nilai tukar rupiah terhadap perekonomian di Indonesia,

maka pergerakan nilai tukar rupiah harus dipantau dan dikendalikan.

Statistical process control (SPC) merupakan pengendalian kualitas statistika dengan memantau dan mengendalikan sebuah proses produksi. Salah satu alat SPC adalah peta kendali. Peta kendali merupakan alat SPC yang digunakan untuk membedakan adanya variasi dari sebab umum (common causes) dan sebab khusus (assignable causes). Variasi dari sebab khusus biasanya berada di luar batas pengendali dan sebab umum berada di dalam batas pengendali. Peta kendali juga memperlihatkan apakah suatu proses dalam keadaan stabil atau tidak. Proses yang stabil (terkendali) menandakan kualitas produk yang baik (Ariani, 2004). Peta kendali pada umumnya dibentuk berdasarkan asumsi kebebasan atau berdistribusi normal pada data observasi. Namun, dalam kenyataannya data tidak selalu berdistribusi normal dan terjadi proses autokorelasi, sehingga keadaan ini akan berpengaruh terhadap pembuatan peta kendali. Asumsi tersebut tentunya harus dipenuhi agar peta kendali yang dihasilkan tidak menimbulkan hasil yang keliru.

Oleh karena itu, untuk data yang mengandung autokorelasi dapat diatasi dengan cara mencari residual dari model peramalan terbaik dan residual tersebut sudah memenuhi asumsi untuk membuat peta kendali.

Peta kendali pertama kali diperkenalkan oleh Walter A. Shewhart pada tahun 1920-an. Menurut Montgomery (2005) kelemahan utama dalam peta kendali Shewhart adalah peta kendali ini hanya menggunakan informasi sampel yang terakhir dan mengabaikan informasi yang diberikan oleh sampel-sampel sebelumnya. Hal ini menyebabkan peta kendali Shewhart kurang sensitif dalam mendeteksi pergeseran proses yang kecil. S.W. Roberts memperkenalkan peta kendali exponentially weighted moving average (EWMA) untuk mendeteksi pergeseran proses yang kecil dalam suatu proses produksi (Montgomery, 2005). Pada peta kendali EWMA, data yang terbaru berhubungan dengan data yang sebelumnya. Data diberi bobot menurun secara eksponential.

Berdasarkan pendahuluan di atas, peneliti tertarik untuk meneliti pergerakan nilai tukar rupiah menggunakan peta kendali EWMA residual.

• 2.    TINJAUAN PUSTAKA

Kualitas

Kualitas merupakan faktor utama dalam sebuah perusahaan atau instansi. Segala upaya dilakukan untuk meningkatkan kualitas. Menurut Feigenbaum (1991) dalam Ariani (2004) mengatakan keseluruhan karakteristik produk dan jasa yang meliputi marketing, engineering, manufacture, dan maintenance, di mana produk dan jasa tersebut dalam pemakaiannya akan sesuai dengan kebutuhan dan harapan pelanggan.

Pengendalian kualitas

Statistical process control (SPC) merupakan pengendalian kualitas statistika dengan memantau dan mengendalikan sebuah proses produksi. Pengendalian kualitas perlu dilakukan untuk memantau dan mengendalikan produk atau jasa agar sesuai dengan standar. Pengendalian kualitas dilakukan sebagai upaya

mengurangi variabilitas atau kesalahan yang dapat menyebabkan produk atau jasa tidak sesuai dengan konsumen.

Salah satu alat pengendalian kualitas statistika atau SPC, yaitu bagan kendali atau peta kendali. Peta kendali memperlihatkan kestabilan suatu proses secara statistika. Peta kendali merupakan alat yang membedakan adanya variasi dari sebab umum (common cause) dan sebab khusus (assignable cause). Variasi dari sebab khusus biasanya berada di luar batas pengendali dan sebab umum berada di dalam batas pengendali (Ariani, 2004).

Peta kendali EWMA

EWMA dapat didefinisikan sebagai berikut (Montgomery, 2005):

Z_i — λx_i + (1 - Λ)z_i_ ₁      (1)

dengan z_i merupakan nilai EWMA pengamatan ke- i, Xi merupakan data pengamatan ke- i, dan λ merupakan nilai pembobot dengan 0 < λ ≤ 1 adalah konstan (sampel pertama pada i = 1) sehingga z₀ — μ₀, dengan μ₀ merupakan rata-rata dari observasi. Lebih lanjut lagi (Montgomery, 2005) menyatakan bahwa dalam praktiknya, nilai λ = 0,05; λ = 0,1; dan λ = 0,2 adalah pilihan yang populer dalam mendeteksi pergeseran proses yang kecil.

Batas kontrol dari peta kendali EWMA adalah :

U CL — Oq + L σ f⅛1-(1-r) , \ ⁽ 2 ^_Z)

^^{l — μ} o ^{,                                  (2)}

LCL = μo — Lσ ∣⅛1-(1-r) , ^{( 2 _}^)

atau

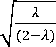
CL =μo ,                       (3)

L CL — Oq

—

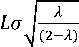
dengan L adalah lebar dari batas kendalinya, adalah rata-rata observasi, adalah simpangan baku dari observasi, upper control limit (UCL) adalah batas kendali atas, central limit (CL) adalah titik tengah, dan lower control limit (LCL) adalah batas kendali bawah.

Deret waktu

Deret waktu didefinisikan sebagai kumpulan observasi yang dibuat secara beruntun atau berurut sepanjang waktu. Biasanya observasi dalam deret waktu bersifat tidak bebas (dependent) atau dapat dikatakan berkorelasi. Sehingga urutan dari observasi menjadi sangat penting (Cryer & Chan, 2008).

Kestasioneran data

Data deret waktu dikatakan stasioner jika rata-rata dan variansnya konstan yang artinya tidak ada unsur tren dan tidak ada unsur musiman dalam data (Cryer & Chan, 2008). Sehingga jika data tidak stasioner dalam rata-rata, maka dilakukan penstasioneran terlebih dahulu dengan metode pembedaan (differencing). Jika data tidak stasioner dalam varians, maka dapat dilakukan dengan transformasi log dan akar kuadrat yang merupakan keluarga power transformation yang disebut Box-Cox transformation. Untuk melihat kestasioneran data, dapat dilakukan dengan uji unit root (akar unit). Uji ini disebut Augmented Dickey-Fuller (ADF) test dengan formulasi sebagai berikut:

H₀ : data tidak stasioner (terdapat unit roots) H₁ : data stasioner (tidak terdapat unit roots)

Statistik Uji : ∆ Y_t = β₁ + β₂t + YY_t _ ₁ + ∑^ i a_iYY_t _ _i + u_t                           (4)

Daerah kritis uji sebagai berikut:

H₀ ditolak apabila nilai p-value < a, dengan taraf nyata a = 0,05. H₀ diterima apabila nilai atau p-value > a, dengan taraf nyata a = 0,05.

Identifikasi model

Setelah data stasioner dilanjutkan dengan mengidentifikasi (menduga) orde AR dan MA yang sesuai dengan menggunakan grafik ACF dan PACF. Jika ACF turun secara eksponensial dan PACF signifikan pada lag p maka proses tersebut merupakan proses AR(p). Sebaliknya jika PACF turun secara eksponensial dan ACF signifikan pada        maka proses tersebut

merupakan proses MA( ).

Menduga parameter

Misalkan adalah suatu parameter pada model ARIMA (mencakup ,  , dan ), maka untuk

menguji signifikan parameter dilakukan uji hipotesis sebagai berikut (Wei, 2006):

H₀ : <5 = 0 (parameter tidak signifikan)

H₀ : <5 ≠ 0 (parameter signifikan)

j

Statistik uji:         t — —-~-            (5)

^j                             s . e.(<^s>)

dengan <5 adalah estimasi parameter dalam model dan s. e. (5) adalah standard error dari nilai estimasi parameter. Daerah kritis uji sebagai berikut:

H₀ ditolak apabila nilai |t|>t^_n__pj atau p -value < a, dengan taraf nyata a = 0,05. H₀ diterima apabila nilai |t| > t(a_n__p) atau p -value > a, dengan taraf nyata a = 0,05.

Menguji kenormalan dan uji white noise

• 1.    Menguji kenormalan

Untuk menguji normalitas residual dapat digunakan uji hipotesis, di antaranya uji Jarque-Bera sebagai berikut:

• :    residual berdistribusi normal

• :    residual tidak berdistribusi normal

Statistik Uji: J = = n       ₊ ⅛^∣

(6)

dengan

,          1∑<⅛→)³

s k e wn e ss = —-------- ∑

, _t .     1 ∑≡⅛_i-⅛⁴

kur tos is = -^-----------2

G⅛ι⅛→) ²⁾

Daerah kritis uji sebagai berikut:

ditolak apabila nilai >         atau -

value <  , dengan taraf nyata — 0,05.

diterima apabila nilai <         atau -

value >  , dengan taraf nyata — 0,05.

• 2.    Uji white noise

Pengujian asumsi white noise menggunakan uji Ljung-Box dengan hipotesis dengan hipotesis sebagai berikut:

Hq : Pi — P2 — '" — Pκ — 0 (residual white noise)

H₁ : minimal satu P∕_c ≠ 0 (residual tidak white noise)

dengan fc = 1,2,..., K.

Statistik Uji : Q = n(n + 2∑ ∑^ ^     (7)

Daerah kritis uji sebagai berikut:

H₀ ditolak apabila nilai Q > χ²^__a^_K__m) atau p-value < α, dengan taraf nyata a — 0,05. diterima apabila nilai <               atau

• -value >  , dengan taraf nyata  — 0,05.

Memilih model terbaik berdasarkan nilai AIC minimum

Adapun kriteria informasi pemilihan model berdasarkan residual menggunakan nilai AIC minimum (Wei, 2006) dengan:

Tl IC (M) = nlnσ^ + 2M .         (8)

dengan adalah banyaknya residual,    adalah

jumlah parameter di dalam model, dan ^ varians dari residual. Pada pemilihan model terbaik yang digunakan untuk meramalkan suatu data dapat    dipertimbangkan dengan

meminimalkan nilai AIC. Karena AIC memperkirakan jumlah relatif dari informasi yang hilang oleh suatu model, sehingga semakin sedikit informasi yang hilang semakin tinggi kualitas model tersebut. Oleh karena itu, dipilihlah nilai AIC terkecil. (Wei, 2006).

• 3.    METODE PENELITIAN

Data yang digunakan dalam penelitian ini adalah kurs beli rupiah terhadap dolar Amerika Serikat dengan data kurs harian yang dapat diakses melalui situs http://bi.go.id dengan periode Oktober 2017 sampai Mei 2018. Langkah-langkah dari penelitian ini sebagai berikut:

• 1.    Memplot data untuk melihat data stasioner atau belum dalam rata-rata dan varians. Bila data belum stasioner dalam rata-rata, maka data perlu dilakukan differencing. Bila data belum stasioner dalam varians, maka perlu dilakukan transformasi.

• 2.    Apabila data sudah stasioner, dilanjutkan dengan mengidentifikasi model dengan melihat plot dari ACF dan PACF.

• 3.    Menduga parameter dengan metode maximum likelihood.

• 4.    Melakukan uji kenormalan dengan uji Jarque-Bera dan uji white noise pada sisaan (residual).

• 5.    Memilih model terbaik berdasarkan nilai AIC yang minimum.

• 6.    Membuat peta kendali EWMA residual yang diperoleh dari model peramalan terbaik.

• 7.    Interpretasi dari peta kendali EWMA residual.

• 4.    HASIL DAN PEMBAHASAN

Deskriptif data

Gambar 4.1, memperlihatkan plot nilai tukar rupiah terhadap dolar Amerika Serikat pada periode Oktober 2017 sampai Mei 2018. Berdasarkan plot data terjadi fluktuasi cukup tajam dan dapat dilihat adanya tren naik, yang mengindikasikan bahwa dolar Amerika Serikat semakin menguat dan rupiah melemah.

Data nilai tukar rupiah terhadap dolar Amerika Serikat merupakan data deret waktu yang artinya bahwa data sekarang dipengaruhi oleh data sebelumnya. Sehingga data nilai tukar rupiah terhadap dolar Amerika Serikat bersifat tidak bebas atau berautokorelasi.

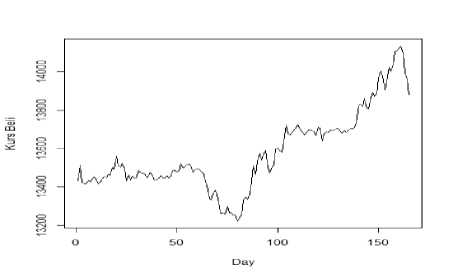
Gambar 1. Kurs Beli Rupiah Terhadap Dolar Amerika Serikat periode Oktober 2017 sampai Mei 2018

Kestasioneran Data

Melihat kestasioneran data dapat dilihat berdasarkan plot dari data dan menggunakan uji

akar unit Augmented Dickey-Fuller (ADF). Apabila data belum stasioner, dapat dilakukan transformasi dan differencing pada data sampai data stasioner.

• 1.    Plot data

Gambar 4.1, dapat dilihat bahwa data mengandung tren naik, sehingga data kurs rupiah belum stasioner. Agar deret tersebut stasioner, maka data perlu ditransformasi dan didifferencing.

• 2.    Mengidentifikasi stasioner dengan menggunakan uji unit-root (akar unit)

• i.    Melihat kestasioneran melalui uji unit root dengan uji ADF pada data nilai tukar rupiah terhadap dolar Amerika Serikat. Berdasarkan uji ADF, diperoleh nilai statistik uji Dickey-Fuller = -2.1044 dengan nilai p — value = 0.5328, karena p — aalue > a = 0.05, maka kesimpulannya adalah data nilai tukar rupiah terhadap dolar Amerika Serikat tidak stasioner.

• ii.    Melihat kestasioneran melalui uji unit root dengan uji ADF pada data nilai tukar rupiah terhadap dolar Amerika Serikat yang telah ditransformasi dan didifferencing. Berdasarkan uji ADF, diperoleh nilai statistik uji Dickey-Fuller = —3.5913 dengan nilai p — v alue = 0.03622, karena p — aalue < a = 0.05, maka kesimpulannya adalah data nilai tukar rupiah terhadap dolar Amerika Serikat yang telah didifferencing satu kali dan ditransformasi sudah stasioner.

Identifikasi model

Setelah data stasioner, selanjutnya mengidentifikasi model dengan melihat pola dari plot ACF dan PACF dari data kurs beli rupiah terhadap dolar Amerika Serikat yang sudah ditransformasi dan didifferencing.

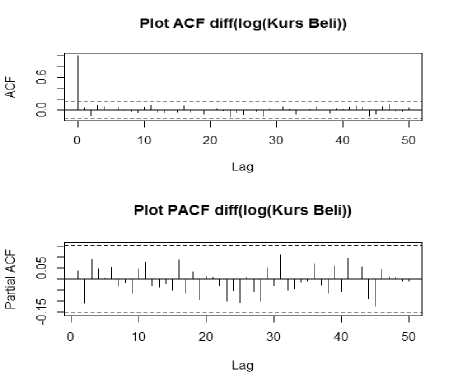
Gambar 2. Plot ACF Dan PACF Kurs Beli Rupiah Terhadap Dolar AS yang ditransformasi dan didifferencing

Berdasarkan Gambar 2, dapat dilihat bahwa plot ACF dan PACF melemah setelah lag 2 dan 3 sebelumnya telah diperoleh data yang stasioner setelah data nilai tukar rupiah terhadap dolar Amerika Serikat ditransformasi dan didifferencing satu kali, sehingga ada beberapa kandidat model yang dapat dibuat untuk meramalkan nilai tukar rupiah terhadap dolar Amerika Serikat, yaitu: ARIMA(1,1,0), ARIMA(2,1,0),ARIMA(3,1,0), ARIMA(0,1,1), ARIMA(0,1,2) ARIMA(1,1,1), ARIMA(2,1,3), dan ARIMA(3,1,2).

Menduga parameter

Dari beberapa model, diperoleh bahwa model ARIMA(1,1,1) yang parameternya signifikan dikarenakan |t| > t^a_n__py

Menguji kenormalan dan white noise

Setelah menduga parameter, selanjutnya akan diuji residual yang diperoleh dari masing-masing model.

• 1.    Uji kenormalan Jarque-Bera

Hasil yang diperoleh dari uji kenormalan uji Jarque-Bera dengan software R, diperoleh bahwa model ARIMA(1,1,0), ARIMA(0,1,1), dan ARIMA(1,1,1) yang berdistribusi normal dan model lainnya tidak berdistribusi normal.

Tabel 1. Uji kenormalan residual beberapa model

Model	p-value	Uji kenormalan
ARIMA(1,1,0)	0.07888	Normal
ARIMA(2,1,0)	0.03181	Tidak normal
ARIMA(3,1,0)	0.03204	Tidak normal
ARIMA(0,1,1)	0.08251	Normal
ARIMA(0,1,2)	0.03778	Tidak normal
ARIMA(1,1,1)	0.06266	Normal
ARIMA(2,1,3)	0.02593	Tidak normal
ARIMA(3,1,2)	0.01691	Tidak normal

Alpha yang digunakan a = 0,05, p - aaIue > 0,05

mengartikan bahwa residual dari model peramalan berdistribusi normal.

• 2.    Uji white noise

Hasil yang diperoleh dari uji white noise dengan software R, diperoleh bahwa semua model memenuhi asumsi white noise. Sehingga residual dari semua model ini bersifat bebas atau independent.

Tabel 2. Uji white noise residual beberapa model

Model	p-value	Uji white noise	AIC
ARIMA(1,1,0)	0.581	White noise	1632,11
ARIMA(2,1,0)	0.9022	White noise	1632,1
ARIMA(3,1,0)	0.9865	White noise	1631,86
ARIMA(0,1,1)	0.5845	White noise	1632,01
ARIMA(0,1,2)	0.9152	White noise	1631,88
ARIMA(1,1,1)	0.8077	White noise	1632,49
ARIMA(2,1,3)	0.9913	White noise	1635,09
ARIMA(3,1,2)	0.9988	White noise	1635,26

Alpha yang digunakan a = 0,05, p - aalee > 0,05

mengartikan bahwa residual dari model peramalan memenuhi asumsi white noise, sehingga residual bersifat bebas atau independent.

Memilih model terbaik berdasarkan nilai AIC minimum

Setelah melakukan pemeriksaan diagnostik, selanjutnya memilih model terbaik berdasarkan nilai AIC minimum. Karena diperoleh satu-satunya model, yaitu ARIMA(1,1,1) yang memenuhi asumsi kenormalan dan uji white noise, serta parameternya signifikan. Sehingga ARIMA(1,1,1) dipilih sebagai model terbaik.

Membuat peta kendali EWMA

• 1.    Menentukan nilai lambda (bobot) yang paling efektif.

Menentukan nilai lambda yang paling efektif dalam membuat peta kendli EWMA, yaitu dengan melihat seberapa banyak titik mengalami pergeseran dan ditemukan pola yang paling signifikan memberikan informasi tingkah laku pola grafik yang tidak random pada setiap lambda yang dicobakan (Antono, dkk, 2016) . Lambda 0,05; 0,1; dan 0,2 merupakan lambda yang populer digunakan untuk mendeteksi pergeseran mean proses yang kecil pada peta kendali EWMA (Montgomery, 2005). Sehingga peneliti ingin mencobakan pada ketiga lambda tersebut dan menemukan satu lambda alternatif yang mampu mendeteksi pergeseran kecil.

• a.    Peta kendali EWMA dengan lambda 0,2

Peta Kendali EWMA residual Kurs Beli

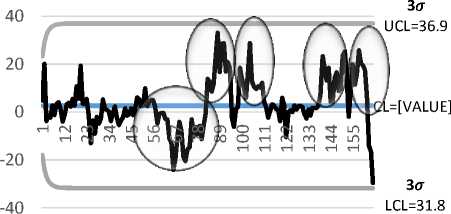
Gambar 3. Peta Kendali EWMA residual dengan λ = 0,2 dan L = 3

Berdasarkan Gambar 3. dapat dilihat bahwa terdapat lima kelompok pergeseran mean. Kelompok pertama terdapat 25 data (15,5%) di bawah nilai tengah dari data ke- 58 sampai data ke- 82. Kelompok kedua terdapat 12 data (7,27%) di atas nilai tengah dari data ke- 83 sampai data ke- 94. Kelompok ketiga terdapat 12

data (7,27%) di atas nilai tengah dari data 99 sampai data ke- 110. Kelompok keempat terdapat 14 data (8,48%) di atas nilai tengah dari data ke-139 sampai ke- 152. Kelompok kelima terdapat 9 data (5,45%) di atas nilai tengah dari data ke-154 sampai ke- 162. Banyaknya kelompok pergeseran mean ini menandakan proses tidak stabil sehingga = 0,2 cukup sensitif dalam mendeteksi pergeseran mean proses yang kecil.

• b.    Peta kendali EWMA dengan lambda 0,1

Peta Kendali EWMA residual Kurs

40

20

0

-20

-40

EWMA Chart of residual kurs beli

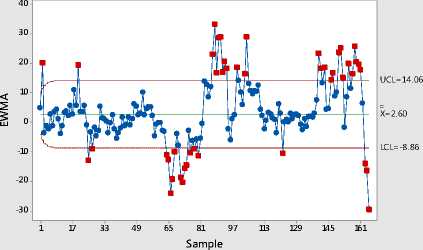
Gambar 4. Peta Kendali EWMA residual dengan =0,2 dan =1

Berdasarkan Gambar 4. dapat dilihat bahwa pada lebar batas kendali 1 ditemukan empat kelompok yang keluar dari batas kendali dan total titik yang keluar dari batas kendali 1 adalah 45 data (27,3%).  Kelompok pertama

terdapat 5 data (3,03%) yang keluar dari batas bawah 1   dari data ke- 64 sampai ke- 68.

Kelompok kedua terdapat 5 data (3,03%) yang keluar dari batas bawah 1 dari data ke- 71 sampai ke- 74. Kelompok ketiga terdapat 8 data (4,84%) yang keluar dari batas atas 1 dari data ke- 87 sampai ke- 94. Kelompok keempat

terdapat 5 data (3,03%) yang keluar dari batas atas 1 dari data ke-157 sampai ke- 161. Berdasarkan penjelasan di atas, bahwa pada = 0,2 banyak titik yang mengelompok dan keluar dari batas 1 yang membuat proses menjadi tidak stabil. Sehingga, bobot 0,2 menunjukkan bahwa peta kendali lebih sensitif terhadap pergeseran mean.

Gambar 5. Peta Kendali EWMA residual dengan =0,1 dan =3

Berdasarkan Gambar 5. dapat dilihat bahwa terdapat empat kelompok pergeseran mean. Kelompok pertama terdapat 25 data (15,15%) di bawah nilai tengah dari data ke- 58 sampai data ke- 82. Kelompok kedua terdapat 10 data

(6,06%) di atas nilai tengah dari data ke- 86 sampai data ke- 95. Kelompok ketiga terdapat 20 data (12,12%) di atas nilai tengah dari data 97 sampai data ke- 116. Kelompok keempat terdapat 24 data (14,54%) di atas nilai tengah dari data ke-  139 sampai ke- 162. Setelah bobot

diturunkan dari 0,2 menjadi 0,1 diperoleh bahwa terdeteksi pergeseran mean yang semakin melebar. Sebelumnya =0,2 pada kelompok ketiga terdapat 12 data (7,27%) di atas nilai tengah. Ketika =0,1 pada kelompok ketiga terdapat 20 data (12,12%) di atas nilai tengah. Sehingga, penurunan bobot ( ) dari 0,2 ke 0,1 menunjukkan pergeseran mean yang semakin melebar. Sehingga dapat dikatakan bahwa = 0,1 lebih sensitif dari 0,2 untuk mendeteksi

pergeseran mean.

Gambar 6. Peta Kendali EWMA residual dengan =0,1 dan =1

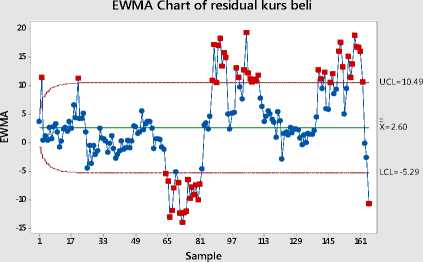
Berdasarkan Gambar 6. dapat dilihat bahwa pada batas kendali 1σ ditemukan lima kelompok yang keluar dari batas kendali dan total titik yang keluar dari batas kendali 1σ adalah 54 data (32,8%). Kelompok pertama terdapat 5 data (3,03%) yang keluar dari batas bawah 1σ dari data ke- 64 sampai ke- 68. Kelompok kedua terdapat 12 data (7,27%) yang keluar dari batas bawah 1σ dari data ke- 70 sampai ke- 81. Kelompok ketiga terdapat 8 data (4,84%) yang keluar dari batas atas 1σ dari data ke- 87 sampai ke- 94. Kelompok keempat terdapat 8 data (4,84%) yang keluar dari batas atas 1σ dari data ke-103 sampai ke- 110. Kelompok kelima terdapat 8 data (4,84%) yang keluar dari batas atas 1σ dari data ke-155 sampai ke- 162. Setelah bobot diturunkan dari lambda 0,2 menjadi 0,1, terjadi pergeseran mean yang semakin melebar. Pada Λ = 0,2, data ke-103 sampai ke-110 berada di dalam batas kendali 1 σ. Sedangkan pada lambda 0,1, data ke-103 sampai ke-110 berada di luar batas kendali 1 . Hal ini berarti bahwa pada data ke-103 sampai ke-110 dengan = 0,1 bergeser semakin menjauh dari nilai tengah. Sehingga, dapat dilihat bahwa = 0,1 dianggap lebih efektif dalam mendeteksi pergeseran mean proses dibandingkan = 0,2.

c. Peta kendali EWMA dengan lambda 0,05

30

Peta Kendali EWMA residual Kurs Beli

Gambar 7. Peta Kendali EWMA residual dengan λ = 0,05 dan L = 3

Berdasarkan Gambar 7. dapat dilihat bahwa terdapat empat kelompok pergeseran mean. Kelompok pertama terdapat 29 data (17,58%) di bawah nilai tengah dari data ke-58 sampai data ke-86. Kelompok kedua terdapat 7 data (4,24%) di atas nilai tengah dari data ke-88 sampai data ke-94. Kelompok ketiga terdapat 20 data (12,12%) diatas nilai tengah dari data ke-99

samapai data ke-118. Kelompok keempat terdapat 24 data (14,55%) di atas nilai tengah dari data ke-140 sampai ke-163. Setelah bobot diturunkan menjadi 0,05 dari lambda 0,1 dapat dilihat bahwa dengan menurunkan bobot dari 0,1 ke 0,05 tidak menunjukkan pergeseran yang halus pada titik-titik untuk mendeteksi pergeseran mean yang melebar atau mendeteksi adanya kelompok lain.

EWMA Chart of residual kurs beli

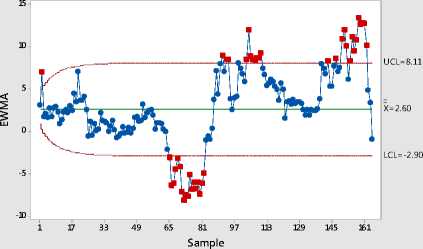
Gambar 8. Peta Kendali EWMA residual dengan λ = 0,05 dan L = 1

Berdasarkan Gambar 8. dapat dilihat bahwa pada lebar batas kendali 1 ditemukan tiga kelompok yang keluar dari batas kendali dan total titik yang keluar dari batas kendali 1 adalah 44 data (26,7%). Kelompok pertama terdapat 18 data (10,9%) yang keluar dari batas bawah 1 σ dari data ke-65 sampai ke-82. Kelompok kedua terdapat 8 data (4,85%) yang keluar dari batas bawah 1 dari data ke-103 sampai ke-110. Kelompok ketiga terdapat 9 data (5,45%) yang keluar dari batas atas 1 dari data ke-154 sampai ke-162. Setelah bobot diturunkan menjadi 0,05 dari bobot 0,1 diperoleh bahwa awalnya data ke-87 sampai ke-94 berada di luar batas kendai 1 pada lambda 0,1. Tapi data ke-87 sampai ke-94 pada lambda 0,05 berada dalam batas kendali 1 .

Hal ini berarti bahwa titik-titik pada lambda 0,05 kurang sensitif mendeteksi pergeseran mean proses yang kecil. Sehingga dari ketiga lambda yang dicobakan pada residual model peramalan ARIMA(1,1,1) kurs beli rupiah terhadap dolar Amerika Serikat, diperoleh bahwa = 0,1 yang paling efektif untuk mendeteksi pergeseran mean proses yang kecil.

Interpretasi Peta Kendali EWMA

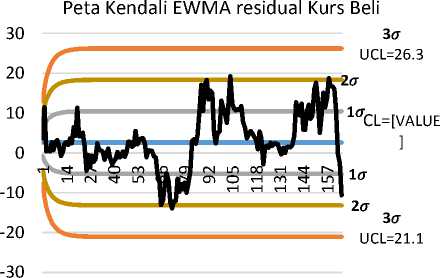
Gambar 9. Peta Kendali EWMA residual dengan λ = 0,1 dan L = 1,2,3

Peta Kendali EWMA Kurs Beli 14200

13000

12800

Γ^^(Y)σ)lΛΓ^^(Y)σ)Lnr^ Hω'tωcoσ)HN^∙ιo

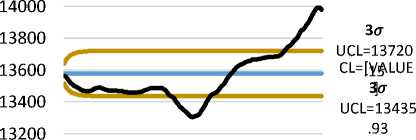
Gambar 10. Peta Kendali EWMA observasi dengan = 0,1 dan = 3

Berdasarkan Gambar 4.10 dapat dilihat bahwa pada peta kendali EWMA observasi kurs beli rupiah terhadap dolar AS terdapat data yang out of control, sehingga proses tidak stabil. Akan tetapi, penyebab out of control pada observasi disebabkan oleh data yang mengandung autokorelasi. Karena asumsi untuk membuat batas pengendali pada peta kendali EWMA adalah data harus independen dan berdistribusi normal. Oleh sebab itu, asumsi kebebasan dan kenormalan pada data untuk membuat peta kendali EWMA perlu dipenuhi. Apabila tidak, maka bisa menimbulkan peringatan palsu.

Berdasarkan Gambar 4.9 dapat dilihat bahwa residual berada di dalam batas pengendalian yang berarti tidak ada data yang out of control, akan tetapi data mengalami pergeseran mean atau terdapat beberapa hal yang menyebabkan proses tidak stabil. Beberapa hal yang menyebabkan proses tidak terkendali pada

λ = 0,1 yaitu terdapat 4 titik dari 5 berturut-turut berada di luar batas 1 σ, yaitu pada data ke-64 sampai ke-68, data ke-70 sampai ke-81, data ke-87 sampai ke-94, data ke-103 sampai ke-110, dan data ke-155 sampai ke-162. Pelanggaran selanjutnya 15 titik berurutan di satu sisi CL pada data ke-24 sampai ke-47. Proses tidak terkendali disebabkan oleh variasi dari sebab umum karena data residual berada di dalam batas pengendali dan terdapat beberapa pelanggaran. Variasi dari sebab umum merupakan hal-hal yang melekat pada sistem. Pada kasus ini, hal tersebut bisa meliputi ekspor, impor, harga minyak, dan faktor lainnya. Sehingga, dari pihak Bank Indonesia dan pihak yang bekerja di bidang keuangan perlu memperhatikan secara khusus penyebab ketidakstabilan nilai tukar rupiah terhadap dolar Amerika Serikat agar periode berikutnya menjadi lebih stabil atau terkendali

5. KESIMPULAN DAN SARAN

Kesimpulan yang dapat diambil dari hasil dan pembahasan yang telah diperoleh pada penelitian adalah setelah di plot peta kendali EWMA observasi dari data kurs beli rupiah terhadap dolar Amerika Serikat terdapat data yang out of control, sehingga proses tidak stabil. Akan tetapi, penyebab out of control pada observasi disebabkan oleh data yang mengandung autokorelasi. Model peramalan ARIMA terbaik yang diperoleh dari data kurs beli rupiah terhadap dolar Amerika Serikat dengan data harian berjumlah 165 pada periode Oktober 2017 sampai Mei 2018 adalah ARIMA(1,1,1). Setelah dicobakan =— 0,2; 0,1; dan 0,05, diperoleh λ = 0,1 sebagai lambda yang paling efektif untuk mendeteksi pergeseran mean proses yang kecil. Setelah di plot peta kendali EWMA residual dari model peramalan ARIMA(1,1,1) dengan λ = 0,1 diperoleh bahwa residual tidak terkendali. Sehingga, kurs beli rupiah terhadap dolar Amerika Serikat tidak terkendali (stabil).

Dalam penelitian ini, untuk menghilangkan sifat autokorelasi pada observasi digunakan residual model peramalan terbaik untuk membuat

peta kendali. Pada penelitian selanjutnya diharapkan bisa mengatasi sifat autokorelasi data dengan cara lain, yaitu dengan peta kendali EWMA yang dimodifikasi. Apabila ingin mendeteksi pergeseran besar dan kecil dalam satu bagan, bisa digunakan peta kendali Shewhart-EWMA. Apabila ingin membuat peta kendali tanpa asumsi kenormalan, bisa menggunakan peta kendali Non-parametric EWMA. Apabila ingin membuat peta kendali pada data lebih dari satu variabel yang diukur, bisa menggunakan peta kendali Multivariat EWMA (MEWMA).

DAFTAR PUSTAKA

Antono, I., Santoso, R., & Wilandari, Y. (2016). Komputasi Metode Exponentially Weighted Moving Average Untuk Pengendalian Kualitas Proses Produksi Menggunakan GUI Matlab (Studi Kasus : PT Djarum Kudus SKT Brak Megawon III). Jurnal Gaussian, Volume 5, Nomor 4, Tahun 2016, Halaman 673-682.

Ariani, D. W. (2004). Pengendalian Kualitas Statistik (Pendekatan Kuantitatif dalam Manajemen Kualitas). Yogyakarta: Andi.

Bank Indonesia. (2017). Tujuan Kebijakan Moneter. Retrieved from https://www.bi.go.id/id/moneter/tujuan-kebijakan/Contents/Default.aspx

Cryer, J., & Chan, K.-S. (2008). Time Series Analysis with Applications in R, Second Edition . New York: Springer.

Montgomery, D. C. (2005). Introduction to Statistical Quality Control Fifth Edition. New York: John Wiley & Sons, Inc.

Wei, W. W. (2006). Time Series Analysis Univariate and Multivariate Methods Second Edition. Philadelphia: Addision Wesley.

73