KENDALI MPC BERBASIS FILTER KALMAN UNTUK SISTEM EMPAT TANGKI
on
E-Jurnal Matematika Vol. 8(1), Januari 2019, pp. 48-54
DOI: https://doi.org/10.24843/MTK.2019.v08.i01.p234
ISSN: 2303-1751
KENDALI MPC BERBASIS FILTER KALMAN UNTUK SISTEM EMPAT TANGKI
Zaiful Ulum1§, Moh. Affaf2
1STKIP PGRI Bangkalan [zaifululum@stkippgri-bkl.ac.id] 2STKIP PGRI Bangkalan [mohaffaf@stkippgri-bkl.ac.id] §Corresponding Author
ABSTRACT
A Four-tank system is a multi-input multi-output (MIMO) system consisting of four interconnected water tanks and two pumps. This paper deals with the control design of the four-tank system using model predictive control (MPC) based filter Kalman. The objective of the control design is to regulate the output of the system towards the desired values. In this work, the optimal control to the system is determined by means MPC controller where both output and input constraints to the system are explicitly considered. The filter Kalman is used to estimate the state of the system. Simulations by using Matlab are performed to verify the performance of the proposed control design. Simulation results show that the proposed control design can regulate the output of the system towards the desired values.
Keywords: four-tank system, MPC, filter Kalman
Sistem empat tangki merupakan plant laboratorium yang telah terbukti cocok digunakan untuk menguji proses industri (Kirubakaran et al, 2014). Masalah kendali sistem empat tangki adalah membawa level air pada tangki menuju level yang diinginkan (water level control). Water lavel control memiliki peranan yang sangat krusial dalam dunia industri .
Beberapa penelitian terkait water lavel control telah dilakukan oleh peneliti. Selamat et al (2015) menggunkan kontroler LQR dan PID untuk desain kendali pada sistem dua tangki. Herlambang et al (2017) menggunakan kontroler DSMC yang diaplikasikan pada steam drum boiler. Khalid et al. (2014) merancang desain kendali pada sistem empat tangki menggunakan kontroler JST. Namun demikian, desain kendali tersebut tidak memperhatikan batasan baik input maupun output sistem. Padahal dalam dunia industri, kebanyakan sistem yang ada mempunyai batasan. Oleh karena itu dalam merancang kendali harus
diperhatikan batasan pada sistem agar diperoleh desain kendali yang lebih aplikatif.
Salah satu kontroler yang memperhatikan batasan pada sistem baik input maupun output secara eksplisit dalam menentukan kendali adalah kendali model prediktif (model predictive control/MPC). Kendali MPC adalah metode kendali optimal yang menggunakan sebuah model untuk memprediksi output sistem sepanjang horison prediksi dan menggunakan prinsip horison mundur. (Maciejowski,) Input kendali sistem pada setiap waktu diskrit diperoleh dengan menentukan barisan kendali optimal yang meminimalkan suatu fungsi cost dan memenuhi suatu kendala. Elemen pertama dari barisan kendali optimal tersebut kemudian diaplikasikan ke sistem. Input kendali pada waktu diskrit berikutnya dihitung dengan mengulangi langkah-langkah yang menggunakan prinsip horison mundur.
Salah satu penelitian tentang aplikasi MPC pada sistem empat tangki telah dilakukan oleh Ulum (2017). Namun demikian, pada penelitian
tersebut tidak diperhatikan derau (noise) baik pada proses maupun pengukuran. Pada umumnya sistem yang ada memuat noise yang disebabkan oleh adanya gangguan pada sistem maupun penuruan persamaan dinamis yang kurang sesuai dengan sistem sebenarnya. Untuk menyempurnakan penelitian yang telah dilakukan oleh Ulum (2017), pada penelitian ini akan dirancang desain kendali sistem empat tangki menggunakan MPC berbasis filter Kalman. Pada penelitian ini diperhatikan noise pada proses dan pengukuran.
Pembahasan pada paper ini tersusun sebagai berikut. Bagian 2 menjelaskan model sistem empat tangki beserta persamaan dinamisnya. Formulasi desain kendali MPC diberikan pada Bagian 3. Bagian 4 menjelaskan tentang filter Kalman. Pada Bagian 5 diberikan hasil simulasi. Akhirnya, simpulan dan saran diberikan pada Bagian 6.
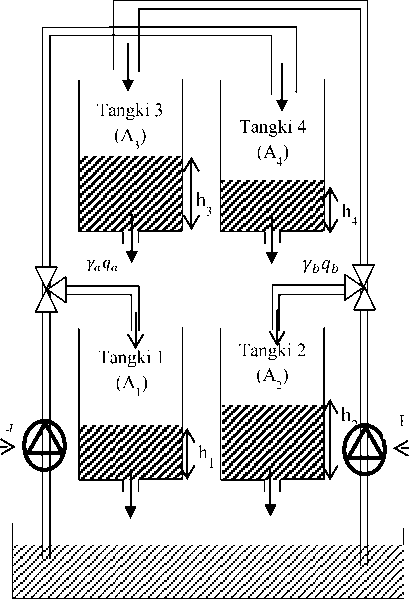
Sistem empat tangki yang digunakan pada penelitian ini diberikan oleh Gambar 1.
1 — YbCb
1 — YaCa
Pompa a
Cla
Pompa b
Clb
Gambar 1. Skema Sistem Empat Tangki
Untuk masing-masing tangki i = 1, .,4, berdasarkan hukum kekekalan massa dan hukum Bernoulli, laju perubahan volume tangki i diberikan oleh persamaan berikut.
dh
Ai i = qin - qout , qout = ai 2ghi .
dt i i i
dengan A [cm2] adalah luas permukaan tangki
i, h [cm] adalah tinggi air pada tangki i, a [cm2 ] adalah luas permukaan saluran keluar tangki i, g[cms-2 ] adalah percepatan gravitasi bumi, dan q [cm-3s-1] serta q [cm-3s-1] adalah aliran masuk ke tangki i dan aliran keluar dari tangki i.
Aliran masing-masing pompa j, j = a, b, dibagi secara proporsional berdasarkan dua parameter γ,γ∈ (0,1) . Dari pompa a,
sebanyak γ q mengalir ke tangki 1 dan sisanya, 1-γ q , mengalir ke tangki 4.
Sedangkan dari pompa b, sebanyak γbqb
mengalir ke tangki 2 dan sisanya, 1-γ q , mengalir ke tangki 3. Diperhatikan juga bahwa aliran keluar dari tangki 3, q , masuk ke tangki 1 dan aliran keluar dari tangki 4 , q , masuk ke tangki 2.
Dengan memperhatikan aliran masuk dan keluar dari semua tangki secara simultan, dinamika sistem empat tangki di atas diberikan oleh (Valencia, 2012).
d h1( t) dt
d h2( t) dt
d h3( t) dt
—
—
α- √2gh^ + a√∑gh^(e)
+ 4qa( t )
√29 h2(t)+a√2gh4(t) ^2 ^2
+ ∣Qδ(O
a3 Ii , r^ , (1 — Yb) ^Γ√ 29 h 3 (O + —;---q b ( t)
λ3
⅛f^ = —^j2^ + ^qa(t) (i)
Nilai-nilai parameter sistem empat tangki di atas diberikan oleh Tabel 1 berikut (Kirubakaran et al., 2014).
Tabel 1. Nilai Parameter Sistem Empat Tangki
|
Parameter |
Nilai |
Satuan |
Deskripsi |
|
nTnax |
20 |
cm |
Tinggi maksimum air pada tangki 1 sampaii 4 |
|
nTnin |
3 |
cm |
Tinggi minimum air pada tangki 1 sampai 4 |
|
Qamax Qbmax |
15.7 16.45 |
cm ⁄ѕ cm ⁄ѕ |
Debit maksimum pompa a dan b |
|
Qmin |
0 |
cm ⁄ѕ |
Debit minimum pompa a dan b |
|
, , |
0.071 0.057 |
cm cm |
Luas permukaan aliran keluar tangki |
|
, , |
28 32 |
cm cm |
Luas permukaan tangki |
|
, |
0.35 |
Proporsi aliran pompa a dan b | |
|
ℎ ℎ |
10.43 15.98 |
cm cm |
Level ekuilibrium tangki 1 dan 2 |
|
ℎ ℎ |
6.60 9.57 |
cm cm |
Level ekuilibrium tangki 3 dan 4 |
|
Qa Qb |
9.89 10.36 |
cm ⁄ѕ cm ⁄ѕ |
Debit ekulibrium pompa a dan b |
Untuk merancang kendali dengan MPC, persamaan (1) di atas dilinierisasi di sekitar titik ekuilibrium (ℎ ,ℎ ,ℎ ,ℎ , , ). Model linier
persamaan (1) diberikan oleh
dengan
()=[ ( ) ( ) ( ) ( )] ,
= √ , =1,2,3,4, dan
|
1 |
— 0 τ3 | ||
|
— τι |
0 | ||
|
0 |
1 |
0 - | |
|
A = |
0 |
τ 2 0 |
τ4 - — 0 |
|
0 |
0 |
τ3 0 -1 | |
|
B |
L 1= *1 |
Ya A1 0 0 - Ya ) A4 |
τι J 0 Yb A 2 . (1 - Yb) A3 0 |
Vektor x dan u pada persamaan (2) di atas menyatakan vektor state dan input sistem. Pada penelitian ini diasumsikan bahwa tidak semua state dapat diukur. State yang dapat diukur hanya level tangki 1 dan 2 yakni dan . Dalam bentuk vektor, output sistem dapat dinyatakan sebagai
()= ( ), (3) dengan
1000 =*0 1 0 0+.
Bentuk diskrit dari persamaan (2) dan (3) dengan waktu sampling =1 diberikan oleh
( +1)= ()+ ( ), (4)
()= ( ),
dengan k menyatakan waktu diskrit dan
|
0.9938 |
0 |
0.0088 |
0 ^ | |
|
Ad = |
0 0 |
0.9938 0 0 0.9912 |
0.0088 0 | |
|
_ 0 |
0 |
0 |
0.9938j | |
|
’ 4.9845 |
0.0516 ^ | |||
|
Bd = |
0.0516 0 |
4.9845 11.6150 | ||
|
_11.6305 |
0 j | |||
-
3. FORMULASI DESAIN KENDALI MPC
Kendali MPC adalah metode kendali optimal yang menggunakan sebuah model untuk memprediksi output sistem sepanjang horison prediksi dan menggunakan prinsip horison mundur (Maciejowski, 2002). Input kendali sistem pada setiap waktu diskrit diperoleh dengan menentukan barisan kendali optimal yang meminimalkan suatu fungsi cost dan memenuhi suatu kendala. Elemen pertama dari barisan kendali optimal tersebut kemudian diaplikasikan ke sistem. Input kendali pada waktu diskrit berikutnya dihitung dengan mengulangi langkah-langkah yang menggunakan prinsip horison mundur. Formulasi desain kendali MPC terdiri dari formulasi prediksi output, formulasi kendala dan formulasi fungsi cost.
-
3.1 Prediksi Output
Model yang digunakan untuk memprediksi output adalah persamaan (4). Didefinisikan X(k+j|k), u(k+j|k) dan y(k+j|k) berturut-turut adalah prediksi state, input kendali dan output pada waktu diskrit k+j berdasarkan informasi waktu diskrit k. Didefinisikan juga N adalah panjang horison prediksi. Maka prediksi output y sepanjang horison prediksi N diberikan oleh
Y=Φx(k|k)+ΨU, (5)
dengan
Y=(y(k+1|k), y(k+2|k),…,y(k+N|k)) T,
U=(u(k|k), u(k+1|k),…,u(k+N-1)|k)T,
Φ=(C^a, CA2d,…,CA^ )T,
CBcl 0 ⋯0
Ψ = CAdBd CBd ⋯0
CA^Ba CANd^Bd ⋯⋱ ⋮
-
3.2 Formulasi Kendala
Pada penelitian ini ada dua kendala yang
diperhatikan dalam menentukan kendali optimal
yaitu input kendali u dan kendala output y.
Secara matematis, kendala-kendala dapat ditulis sebagai berikut
Umin ≤U(k)≤Umax , dan
tersebut
(6)
Ymin ≤y(k)≤Ymax , (7)
dengan Umin dan Umax berturut-turut menyatakan batas minuman dan maksimum input kendali U, sedangkan Ymin dan Ymax berturut-turut menyatakan batas minuman dan maksimum output Y.
Dengan memperhatikan persamaan (6), kendala input sepanjang horison prediksi N dapat ditulis
Umin ≤U≤ Umax , dimana
(8)
L sebanyak N J
dan
Umax
Secara sama
L sebanyak N J
kendala output sepanjang horison
prediksi N dapat ditulis menjadi
dimana
(9)
=
L sebanyak N J
dan
V
1max
Selanjutnya,
L sebanyak N J
dengan mensubstitusi persamaan
(5) ke (9), kendala output sepanjang horison prediksi N dapat dinyatakan dalam U sebagai berikut.
*Ѱ+u≤[-Y . ]+*-Φ+X(k|k). (10)
-Ѱ - Φ
-
3.3 Formulasi Fungsi Cost
Tujuan desain kendali pada penelitian ini adalah membawa output y menuju nilai 0 dengan menggunkan input kendali U seminimal mungkin. Oleh karena itu, fungsi cost pada penelitian ini didefinisikan sebagai
J =∑J = I(YT (k+j|k) Qy (k+j)+
UT (k+j-1)R(u(k+j-1))), (11)
dengan Q dan R adalah matriks definit posiif berukuran 2×2. Fungsi cost (11) di atas dapat
dituliskan dalam variabel Y dan U sebagai
berikut. dimana
dan
J= ℚY+ uτℝU,
(12)
ℚ=dlo,Q ( ⏟, Q,…, . ) , ∖sebanyak N/
ℝ=diciQ ( ⏟, R,…,R ).
∖sebaτιyak N/
Selanjutnya dengan mensubstitusikan persamaan (5) ke persamaan (12), diperoleh
J(U;x(k|k))=Ut (Ѱ tℚѰ+ℝ)U
+2(XT (k|k)ΦT ℚѰ) U
+ XT (k|k)ΦT ℚΦX(k|k).
(13) Notasi J(U;x(k|k)) menyatakan bahwa U adalah variabel bebas sedangkan x(k|k) adalah parameter.
Barisan kendali optimal dapat ditentukan dengan menyelesaikan masalah optimisasi berikut.
minuJ(U;x(k|k)) (14)
dengan kendala (8) dan (10).
Untuk menyelesaikan masalah optimisasi (14) di atas terlebih dahulu harus diestimasi nilai state x(k|k) karena pada penelitian ini diasumsikan bahwa tidak semua vektor state x teramati. Untuk mengestimasi vektor state x digunakan metode filter Kalman.
-
4. FILTER KALMAN
Filter Kalman adalah metode estimasi state X untuk sistem yang memuat noise yang berdistibusi normal dengan mean nol (Yathisha & Patilkulkarni, 2018). Untuk mengestimasi state X diperhatikan persamaan (4) dengan adanya noise pada sistem dan pengukuran sebagai berikut.
X(k+1)=Adx(k)+Bdu(k)+ (15)
w(k),
y(k)=Cx (k)+v(k), dengan w dan v berturut-turut menyatakan noise pada sistem yang diasumsikan berdistribusi normal dengan mean 0 dan kovarians Qw dan pengukuran yang berdistribusi normal dengan mean 0 dan
kovarians Bv .
Algoritma filter Kalman terdiri atas dua langkah: update prediksi (prediction update) dan update pengukuran (measurement update). Persamaan update prediksi
diberikan oleh
x(k|k-1)=Adx(k-1|k-1)+Bdu(k), (16) p(k|k-1)=AdP(k-1|k-1)A1d + Qw. (17) Sedangkan persamaan update pengukuran diberikan oleh
K(k)=P(k|k-1)Ct (CP (k|k-1)Ct + Rv )-1 ,
(18)
x(k|k)=x(k|k-1)+
K(k)(y(k)-Cx (k|k-1)), (19)
P(k|k)=(I-K(k)C)P(k|k-1). (20)
-
5. SIMULASI
Untuk menguji performa desain kendali yang telah dirumuskan di atas, dilakukan simulasi menggunakan Matlab. Desain kendali yang dirancang bertujuan untuk membawa output sistem y menuju nilai 0 yang ekuivalen dengan membawa level tangki 1,ℎ , dan tangki 2, ℎ2, menuju level ekuilibrium ℎ° dan ℎ2 . Untuk tujuan simulasi, terlebih dahulu ditetapkan beberapa nilai awal. Nilai awal state dan input kendali berturut-turut ditetapkan X(0) =(5 -6 4 4)T dan U(0)=
(0 0) T. Selanjutnya, panjang horison
prediksi N ditetapkan N=7. Lebih jauh lagi matriks bobot Q dan R pada fungsi cost (11) berturut-turut ditetapakan Q =0.01× ^2 ×2 dan R =0.1× ^2 ×2 . Matriks kovarians Qw dan Rv berturut-turut ditetapkan Qw=0.01× ^4 ×4 daan Rv =0.01× ^2 ×2 . Notasi ^n ×n disini menyatakan matriks identitas dengan ukuran Tl × Tl .
Berdasarkan Tabel 1, kendala input dan output pada persamaan (6) dan (7) dapat ditulis menjadi
dan
Hasil simulasi diberikan oleh gambar berikut. Grafik digambarkan adalah grafik input dan output yang telah ditransformasi dari variabel input [¾ u2]τ dan variabel output [3zι y2 ]τ ke variabel input [Qa Qb]τ dan [⅛1 h2]τ.
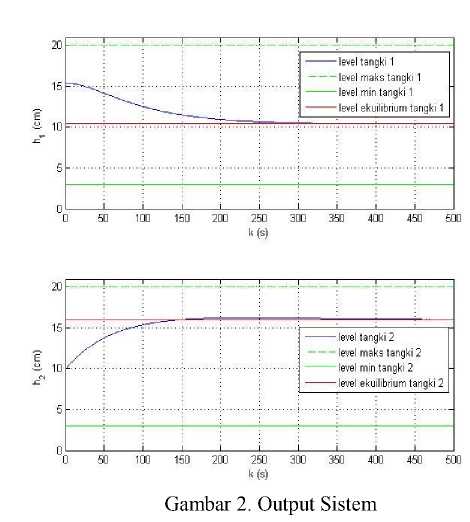
Gambar 2 di atas menunjukkan dinamika output sistem yaitu level tangki 1, h1, dan level tangki 2, h2, selama 500 s. Seperti yang telah dijelaskan di atas tujuan desain kendali adalah membawa level tangki 1 dan tangki 2 menuju level ekuilibriumnya dengan memperhatikan batasan nilai masksimum dan minimum. Berdasarkan gambar tersebut dapat diamati bahwa level tangki 1 maupun level tangki 2 dapat dibawa menuju level ekulibriumnya dari nilai awal yang diberikan. Untuk kasus tangki 1, waktu yang dibutuhkan untuk mencapai level ekuilibrium adalah sekitar 250 s. Sedangkan untuk kasus tangki 2, level ekuilbrium dicapai sekitar 200 s. Lebih jauh lagi dapat diamati bahwa level tangki 1 dan tangki 2 berada pada nilai yang diperbolehkan.
Gambar 3 di bawah ini menggambarkan dinamika debit pompa a, aa, dan pompa b, qb, selama 500 s. Berdasarkan Gambar 3 di atas dapat diamati bahwa debit pompa a dan pompa b berada pada nilai yang
diperbolehkan.
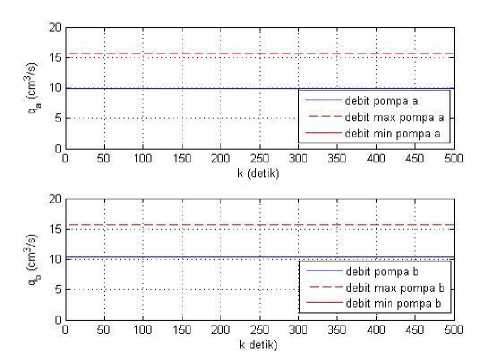
Gambar 3. Input Sistem
Pada penelitian ini diusulkan desain kendali sistem empat tangki menggunakan kendali model prediktif berbasis filter Kalman yang bertujuan untuk membawa ouput sistem yakni level tangki 1 dan tangki 2 menuju level ekuilibriumnya dengan memperhatikan kendala pada output dan input kendali. Hasil simulasi menunjukkan bahwa input kendali mampu membawa output sistem menuju nilai yang diinginkan. Lebih jauh lagi, output dan input kendali berada pada nilai yang diperbolehkan. Hal ini menunjukkan bahwa performa desain kendali yang diusulkan sangat bagus.
Untuk mengurangi beban komputasi, pada penelitian selanjutnya akan dirancang kendali untuk sistem empat tangki menggunakan kendali model prediktif terdistribusi.
DAFTAR PUSTAKA
Herlambang, T., Apriliani,E., Cordova, H., & Mardlijah. 2017. Dynamic Sliding Mode Control (DSMC) Untuk Sistem Kendali Water Level Pada Steam Drum Boiler. Technology Science and Engineering Journal, 1(1), p.34-40
Khalid, U., Shah, Y. A., Qamar, S., Gohar, W., Riaz, R., & Shah, W. A. 2014. Flow and Level Control of Copled Four Tanks System Using Artificial Neural Network. American Journal of Computation, Communication and Control, 1(2), p. 30-35.
Kirubakaran, V. Radharkrishnan, T.K. Sivakumaran, N. 2013. Distributed multiparametric model predictive control design for a quadruple tank process. Measurement. 47 (2014), p.841-854
Maciejowski, J. M. 2002. Predictive Control with Constraints. London, U.K.: PrenticeHall.
Selamat, N. A., Daud, F. S., Jaafar, H. I., & Shamsudin, N. H. 2015. Comparison of LQR and PID Controller Tuning Using PSO for Coupled Tank System. 2015 IEEE 11th International Colloqium on Signal Processing & its Applications (CSPA2015) p. 46-51. Kuala Lumpur: IEEE.
Ulum, Z. 2017. Perancangan Kendali pada Sistem Empat Tangki Menggunakan Kendali Model Prediktif. Jurnal Riset dan Aplikasi Matematika. 1(1), p. 1-7
Valencia, Felipe. 2012. Game Theory Based Distributed Model Predictive Control: An Approach to Large-Scale Systems Control. Universidad Nacional de Colombia. Medellin.
Yathisha, L. Patilkulkarni. 2018. LQR and LQG based optimal switching techniques for PSS and UPFC in power systems. Control Theory and Technology . 16(1), p. 25-37.
54
Discussion and feedback