ESTIMASI NILAI CONDITIONAL VALUE AT RISK (CVaR) PORTOFOLIO MENGGUNAKAN METODE EVT-GJR-VINE COPULA
on
E-Jurnal Matematika Vol. 8(1), Januari 2019, pp. 15-26
DOI: https://doi.org/10.24843/MTK.2019.v08.i01.p230
ISSN: 2303-1751
ESTIMASI NILAI CONDITIONAL VALUE AT RISK (CVaR) PORTOFOLIO MENGGUNAKAN METODE EVT-GJR-VINE COPULA
Ni Wayan Uchi Yushi Ari Sudina1§, Komang Dharmawan2, I Wayan Sumarjaya3
-
1Program Studi Matematika, Fakultas MIPA - Universitas Udayana [Email: uchisudina@gmail.com]
-
2Program Studi Matematika, Fakultas MIPA - Universitas Udayana [Email: k.dharmawan@unud.ac.id]
-
3Program Studi Matematika, Fakultas MIPA - Universitas Udayana [Email: sumarjaya@unud.ac.id]
§Corresponding Author
ABSTRACT
Conditional value at risk (CVaR) is widely used in risk measure that takes into account losses exceeding the value at risk level. The aim of this research is to compare the performance of the EVT-GJR-vine copula method and EVT-GARCH-vine copula method in estimating CVaR of the portfolio using backtesting. Based on the backtesting results, it was found that the EVT-GJR-vine copula method have better performance when compared to the EVT-GARCH-vine copula method in estimating the CVaR value of the portfolio. This can be seen from the statistical values V1, V2, and V of EVT-GJR-vine copula method which is generally smaller than the statistical values V1, V2, and Vcf the EVT-GARCH-vine copula method.
Keywords: Conditional Value at Risk, Vine Copula, GARCH, GJR-GARCH, Extreme Value Theory
untuk meminimumkan risiko. Selain itu, VaR hanya koheren apabila diterapkan pada data yang berdistribusi normal. Metode alternatif untuk mengurangi masalah yang dimiliki oleh VaR yaitu conditional value at risk (CVaR). CVaR memiliki kelebihan antara lain merupakan ukuran risiko koheren dan dapat menghitung risiko pada data berdistribusi normal maupun tidak normal (Danielsson, 2011).
Data finansial memiliki karakteristik yang disebut stylized fact, dicirikan oleh adanya volatility clustering, kebergantungan taklinear, dan ekor gemuk (Danielsson, 2011). Keberadaan ekor gemuk pada data finansial utamanya data return aset finansial mengindikasikan peluang terjadinya nilai ekstrem cukup besar (Zuhara et al, 2012). Guna menghindari kejadian underestimate terhadap risiko, maka keberadaan nilai ekstrem tersebut perlu dimodelkan menggunakan extreme value theory (EVT).
Selain ekor gemuk, cenderung pula terdapat heteroskedastisitas pada data return aset
finansial ditunjukkan oleh adanya volatility clustering yang merupakan fenomena pengelompokan volatilitas pada periode waktu berdekatan. Model generalized ARCH (GARCH) dikembangkan oleh Bollersev pada tahun 1986 guna mengakomodasi efek heteroskedastis yang memiliki karakteristik respons volatilitas simetris terhadap guncangan (Danielsson, 2011). Di beberapa kasus, terdapat gejolak volatilitas yang bersifat asimetris. Sebagai upaya mengakomodasi respon volatilitas asimetris, pada tahun 1994 Glosten, Jagannathan, dan Runkle mengusulkan model yang dikenal dengan Glosten Jagannathan Runkle GARCH (GJR-GARCH) (Brooks, 2008).
Saat melakukan pengukuran risiko portofolio, investor perlu mengetahui struktur kebergantungan antaraset finansial penyusun portofolio. Aset finansial cenderung memiliki kebergantungan yang taklinear. Fenomena kebergantungan taklinear pada aset finansial dapat dilihat dari harga aset yang bergerak relatif independen satu sama lain pada kurun waktu yang lama, namun jatuh secara serentak saat terjadi krisis (Danielsson, 2011).
Copula mempelajari kebergantungan taklinear antarpeubah dalam kasus multivariat. Membentuk copula dalam dimensi tinggi merupakan hal yang sulit dilakukan karena tidak semua jenis copula bivariat dapat diperluas secara rekursif menjadi copula multivariat. Vine copula merupakan solusi alternatif untuk memodelkan kasus multivariat menggunakan copula-copula bivariat (Aas et al., 2009). Copula bivariat yang digunakan dalam penelitian ini yaitu Clayton copula, Gumbel copula, dan Frank copula.
Berdasarkan fenomena tersebut, studi kasus ini bertujuan untuk mengetahui perbandingan kinerja metode EVT-GJR-vine copula dan EVT-GARCH-vine copula dalam mengestimasi CVaR portofolio menggunakan backtesting.
^t ft^t,
ΣTΠ y—1 S
a i? t-1 + ∑ β rf-
i=i ^-ij=ι
(1)
dengan α0 adalah komponen konstanta, ai adalah parameter ARCH, ε%- i adalah kuadrat galat pada waktu t - i, i — 1,2,..., m, βj adalah parameter GARCH, σt2-j∙ adalah varians bersyarat dari kuadrat galat pada waktu t - j, j — 1,2,..., s, dan {zt} merupakan barisan peubah acak IID dengan mean nol dan varians satu (disebut juga inovasi). Adapun z t sering diasumsikan berdistribusi normal atau
berdistribusi student-t (Tsay, 2002).
GJR-GARCH
Glosten, Jagannathan, dan Runkle mengembangkan model GARCH yang mengakomodasi leverage effect. Model ini selanjutnya disebut GJR-GARCH. GJR-GARCH (m, s) didefinisikan sebagai (Brooks, 2008)
^t tz^t,
= αo + ∑( a i ε--i+Yi ε t-iI - -i) + ∑βj t-_ j
dengan I-- i — {1, ^ t - l < 0, serta α 0 >0, a j ≥
-
0, a i+Yi≥0, i — 1,2,,m, dan βj ≥ 0,j — 1,2,,s.
Parameter Yj merupakan pembeda antara model GARCH dan GJR-GARCH.
Extreme Value Theory (EVT)
Secara umum, terdapat dua metode untuk mengidentifikasi nilai ekstrem yaitu block maxima dan peak over threshold (POT). Menurut McNeil et al. (2005) metode block maxima sangat mubazir terhadap data karena data yang teridentifikasi sebagai nilai ekstrem hanyalah data-data amatan yang bernilai maksimum dari setiap blok. Di sisi lain pada metode peak over threshold, data yang teridentifikasi sebagai nilai ekstrem adalah data amatan yang bernilai cukup besar dan melampaui nilai ambang batas (threshold) u. Data-data yang melampaui nilai ambang batas pada metode POT berdistribusi generalized Pareto distribution (GPD).
Teorema 1. (Franke et al., 2011) Jika diberikan fungsi distribusi dengan jumlah observasi yang cukup besar dan fungsi distribusi bersyarat
Fu (y ) untuk nilai U yang cukup besar, maka F-U (y ) dapat dihampiri dengan fungsi distribusi cξ,β(y).
Definisi 1. (Franke et al., 2011) Generalized Pareto distribution dengan parameter skala β>0 dan parameter bentukξ memiliki fungsi distribusi
1
¾ , , (y)=1-(1+⅛) 7
(3)
( ∙y≥0, jikaξ>0;
untuk \ Γ∩ β ■1 iilz□ r dan
*0,-γ+, jika <0;
Gq,β(y)=1-e P, y≥0.
(4)
Chaves-Demoulin (1999) dalam Zuhara et
al. (2012) menyarankan untuk memilih ambang batas ■u pada metode POT sedemikian hingga
data yang berada di atas ambang batas ■u kurang lebih 10 % dari keseluruhan data.
Vine Copula
Vine merupakan graf fleksibel yang digunakan untuk mendeskripsikan copula multivariat menggunakan riam (cascade) copula bivariat yang disebut pasangan copula atau pair copula (Sumarjaya, 2013).
Definisi 2. (Kurowicka & Cooke, 2006) V adalah sebuah vine dengan d elemen apabila
-
1. V={Ti,…,Tci-i};
-
2. T1 merupakan sebuah tree dengan node
^l ={1,…,d } dan edge E1; untuk = 2,…,d-1, T merupakan sebuah tree dengan node Nj = .
V adalah sebuah regular vine dengan d elemen apabila terdapat tambahan yaitu untuk = 2,…,d-1, jika {a,b}∈EJ , maka # aΔb =2, dengan Δ menyatakan symmetric difference.
Reguler vine masih sangat umum dan memiliki sejumlah besar kemungkinan dekomposisi pasangan copula. Terdapat dua keluarga vine yang umum digunakan yaitu C-vine (canonical vines) dan D-vine.
Definisi 3. (Kurowicka & Cooke, 2006) Sebuah regular vine disebut
-
1. D-vine jika masing-masing node pada T1 memiliki derajat paling banyak dua dan
-
2. C-vine jika masing-masing tree T memiliki node unik dengan derajat d-j . Node unik pada T1 disebut akar (root).
Penjabaran selanjutnya difokuskan pada pemaparan materi mengenai C-vine copula.
Secara umum, fungsi densitas C-vine berdimensi n diberikan sebagai berikut (Aas et al,2009):
d d-1 d-J
)=∏f( X„)∏∏cI , | . ,..,l→
m=l j=l i=l '
.{F( xJ | *1 ,…,Xj-I), F(xj+ι| Xi,…,Xj-I)}.
Berdasarkan fungsi densitas C-vine pada Persamaan (5), maka fungsi log likelihood C-vine diberikan oleh (Aas et al., 2009)
d-ld~J n
(X;Θ)=∑∑∑logcJ ,j.|1,..,j-i
j=ι i=ι t=i
[F( xJ ,t| Xi,t,…,Xj-I,t), F(Xj+i,t| Xi,t,…,Xj-I,t)].
(6)
Conditional Value at Risk dan Backtesting
Conditional value at risk (CVaR) merupakan suatu ukuran risiko yang memperhitungkan kerugian melebihi tingkat VaR.
Definisi 4. (Klugman et al., 2008) Value at risk (VaR) dari peubah acak X pada tingkat kepercayaan 100P % adalah P -kuantil fungsi distribusi F dan dinyatakan sebagai
VaR P(X)=Tlp = (P). (7) Expected shortfall atau conditional value at risk (CVaR) dari peubah acak X pada tingkat kepercayaan 100P % merupakan ekspektasi kerugian apabila diketahui besar kerugian yang melebihi P-kuantil dari distribusi peubah acak X. Secara matematis diberikan
CVaR P(X)=E(X|X>VaRP(X)). (8)
Embrechts et al. (2005) memperkenalkan dua ukuran backtesting untuk mengevaluasi kinerja model dalam mengestimasi CVaR.
Ukuran backtesting tersebut yaitu ^l dan ^2 .
Statistik V1 untuk suatu peluang P dirumuskan
sebagai berikut:
Vi
(9)
dengan Wf adalah banyaknya data return yang
digunakan untuk backtesting.
Statistik ½2 dirumuskan sebagai berikut:
∑t=ι Dt 1{Dt>Dp}
V2=∑Wt 1 .
∑ {Dt>Dp}
(10)
dengan Dt=(rt - (-ĈVaRpt )) dan Dp adalah P-kuantil empiris dari {Dt ,t=1,2,…,T}.
Apabila ^i dan ^2 dikombinasikan, maka menjadi statistik V sebagai berikut:
|h|+|h| v =2
(11)
yang mendekati nol apabila model tersebut baik. Apabila suatu estimator CVaR memiliki kinerja yang baik, maka mutlak dari statistik ^l , 1^2, serta statistik V memiliki nilai yang kecil.
Data yang digunakan dalam penelitian ini adalah harga penutupan (closing price) harian indeks saham FTSE Austria (AUT), FTSE Ireland (IRL), dan FTSE Switzerland (SCH) periode 2 Januari 2007 sampai dengan 21 September 2018 sebanyak 3053 observasi. Data tersebut diakses melalui situs
www.investing.com. Langkah-langkah analisis pada penelitian ini yaitu:
-
1. Menghitung return indeks saham.
-
2. Memeriksa stasioneritas pada masing-
masing return indeks saham.
-
3. Memeriksa autokorelasi dan efek ARCH pada return maupun kuadrat return masing-masing indeks saham.
-
4. Memodelkan return indeks saham menggunakan model AR(1)-GJR-t (1,1) dan AR(1)-GARCH-t (1,1).
-
5. Memeriksa kembali efek autokorelasi dan heteroskedastisitas pada residual maupun kuadrat residual model.
-
6. Melakukan plot QQ data residual model dengan distribusi normal standar.
-
7. Memodelkan ekor kiri residual model
dengan GPD.
-
8. Menghitung fungsi distribusi kumulatif
model marginal.
-
9. Melakukan transformasi seragam [0,1].
-
10. Memodelkan distribusi bersama dengan pendekatan vine copula.
-
11. Simulasi return portofolio menggunakan vine copula.
-
12. Menghitung VaR dan CVaR portofolio.
-
13. Membandingkan kinerja metode EVT-GJR-vine copula dan EVT-GARCH-vine copula dalam menghitung CVaR portofolio menggunakan backtesting.
Risiko suatu portofolio dapat dianalisis melalui tingkat pengembalian (return) aset-aset penyusun portofolio tersebut. Oleh karena itu, untuk mengestimasi risiko suatu portofolio maka data harga penutupan harian indeks saham AUT, IRL, dan SCH perlu dikonversi menjadi return.
Tabel 1. Statistik Deskriptif Return Indeks
Saham
Statistik Return Indeks Saham
|
Deskriptif |
AUT |
IRL |
SCH |
|
Mean |
-0,000395 |
-0,000208 |
-0,000004 |
|
Deviasi Standar |
0,019210 |
0,020261 |
0,012060 |
|
Skewness |
-0,092749 |
-0,429981 |
-0,237982 |
|
Kurtosis |
5,416244 |
7,344246 |
8,403218 |
Seperti halnya sebagian besar data deret waktu finansial, return dari indeks saham AUT, IRL, dan SCH tidak berdistribusi normal. Distribusi normal memiliki nilai skewness nol dan nilai kurtosis tiga sedangkan berdasarkan Tabel 1, return dari indeks saham AUT, IRL, dan SCH memiliki nilai skewness negatif dan nilai kurtosis yang lebih besar dari tiga. Nilai skewness yang negatif menunjukkan bahwa return indeks saham AUT, IRL, dan SCH distribusinya memiliki ekor kiri yang lebih panjang daripada ekor kanan. Hal ini berarti return dari ketiga indeks saham tersebut memiliki nilai ekstrem negatif yang lebih banyak, dibandingkan nilai ekstrem positif. Keadaan tersebut mengindikasikan besarnya kemungkinan terjadi kerugian yang disebabkan oleh nilai ekstrem negatif. Di sisi lain, kurtosis dari return indeks saham AUT, IRL, dan SCH yang bernilai lebih besar dari tiga menunjukkan adanya excess kurtosis yang mengindikasikan bahwa return indeks saham AUT, IRL, dan SCH memiliki kurva distribusi yang meruncing (leptokurtis).
Tabel 2. Uji Formal pada Return Indeks Saham
|
Uji Formal (a = 0,05) |
р-value Return Indeks Saham | ||
|
AUT |
IRL |
SCH | |
|
ADF |
0,01 |
0,01 |
0,01 |
|
Ljung-Box Return Sqr.Return |
6,5.10-3 <2 .10 -16 |
1 .10-2 <2 .10 -16 |
6,6 .10-11 <2 .10 -16 |
|
ARCH-LM Return Sqr.Return |
<2 .10 -16 <2 .10 -16 |
<2 .10 -16 <2 .10 -16 |
<2 .10 -16 <2 .10 -16 |
|
corr (rt2 , ⅞-l) |
-0,131 |
-0,079 |
-0,189 |
Suatu data deret waktu belum dapat dianalisis apabila data tersebut belum memenuhi asumsi stasioneritas. Stasioneritas merupakan dasar dari suatu analisis deret waktu (Tsay, 2002). Identifikasi stasioneritas pada return indeks saham dilakukan menggunakan uji augmented Dickey-Fuller (ADF) dengan hipotesis nol yaitu terdapat akar unit pada return indeks saham. Berdasarkan Tabel 2, uji ADF dengan taraf signifikan a = 0,05 pada return indeks saham AUT, IRL, dan SCH menunjukkan р-value=0,01<a = 0,05 sehingga cukup bukti untuk menolak hipotesis nol. Hal ini berarti tidak terdapat akar unit sehingga return indeks saham AUT, IRL, dan SCH stasioner.
Autokorelasi merupakan korelasi antara observasi data pada waktu ke-t dan observasi data pada waktu-waktu sebelumnya (t-1,t-2,…). Uji formal Ljung-Box digunakan untuk memastikan keberadaan efek autokorelasi pada data return dan kuadrat return (sqr. return) dengan hipotesis nol yaitu tidak terdapat autokorelasi pada data. Berdasarkan Tabel 2, uji Ljung-Box pada return dan kuadrat return indeks saham AUT, IRL, dan SCH menunjukkan р-value masing-masing indeks saham kurang dari taraf signifikan a = 0,05 sehingga cukup bukti untuk menolak hipotesis nol mengenai ketiadaan autokorelasi pada data. Hal ini berarti terdapat efek autokorelasi pada return maupun kuadrat return indeks saham AUT, IRL, dan SCH. Keberadaan autokorelasi pada kuadrat return indeks saham mengindikasikan adanya peristiwa pengelompokan volatilitas yang menunjukkan varians data tidak konstan atau disebut dengan heteroskedastisitas.
Keberadaan heteroskedastisitas atau efek ARCH semakin diperjelas melalui hasil uji
formal ARCH-LM pada Tabel 2. Nilai р-value uji ARCH-LM pada return dan kuadrat return masing-masing indeks saham kurang dari taraf signifikan a = 0,05 sehingga cukup bukti untuk menolak hipotesis nol mengenai ketiadaan efek ARCH. Hasil ini menunjukkan bahwa terdapat efek ARCH pada return maupun kuadrat return indeks saham AUT, IRL, dan SCH.
Selain keberadaan efek ARCH, pada data return indeks saham AUT, IRL, dan SCH terdeteksi pula keberadaan efek asimetris atau dikenal juga dengan leverage effect. Efek asimetris merupakan respons volatilitas yang berbeda terhadap kenaikan dan penurunan return aset. Guncangan negatif lebih meningkatkan volatilitas dibandingkan guncangan positif (good news). Zivot (2008) menyarankan pengujian efek asimetris dengan menghitung nilai korelasi antara kuadrat return aset rt dan return aset pada periode ke t-1 yaiturt_1 . Nilai korelasi yang negatif mengindikasikan keberadaan efek asimetris pada data. Berdasarkan Tabel 2, nilai korelasi antara kuadrat return aset dan return aset pada periode ke t-1 bernilai negatif untuk masing-masing return indeks saham. Hal ini menunjukkan adanya efek asimetris pada return indeks saham AUT, IRL, dan SCH.
Berdasarkan identifikasi data yang telah dilakukan, keberadaan efek autokorelasi pada ketiga return indeks saham mengindikasikan bahwa pemodelan rataan bersyarat perlu diterapkan pada return indeks saham AUT, IRL, dan SCH. Di sisi lain, keberadaan efek asimetris, heteroskedastisitas, dan autokorelasi pada return dan kuadrat return indeks saham AUT, IRL, dan SCH perlu diakomodasi menggunakan model heteroskedastisitas asimetris. Pada penelitian ini, model heterokedastisitas asimetris yang digunakan untuk memodelkan varians return indeks saham AUT, IRL, dan SCH yaitu Glosten, Jagannathan, dan Runkle GARCH disingkat GJR. Sebagai pembanding, diterapkan pula model heteroskedastisitas simetris yaitu GARCH (1,1) yang dalam berbagai literatur dinyatakan dapat mengakomodasi efek heteroskedastisitas pada data finansial dengan baik.
Berdasarkan studi empiris yang dilakukan oleh McNeil & Frey (2000) dan Huang et al. (2011), maka pada penelitian ini diterapkan dua model yang berbeda pada return masing-masing indeks saham yaitu model AR(1)-GARCH(1,1) dan AR(1)-GJR(1,1). Inovasi distribusi yang digunakan untuk memodelkan galat dari model heteroskedastisitas bersyarat pada penelitian ini yaitu distribusi student-t guna mengakomodasi keberadaan ekor gemuk pada distribusi return indeks saham AUT, IRL, dan SCH.
Pengujian efek ARCH dan autokorelasi perlu dilakukan pada residual model AR(1)-GARCH(1,1) dan AR(1)-GJR(1,1) untuk mengetahui keefektifan kinerja model GARCH-t(1,1) dan GJR-t(1,1) dalam mengakomodasi keberadaan efek ARCH dan autokorelasi pada
return indeks saham AUT, IRL, dan SCH. Berdasarkan Tabel 3, р - value uji Ljung-Box masing-masing residual dan kuadrat residual model lebih besar daripada taraf signifikan a = 0,05 sehingga tidak cukup bukti untuk menolak hipotesis nol. Hal ini mengindikasikan ketiadaan efek autokorelasi pada residual maupun kuadrat residual model AR(1)-GARCH-t(1,1) dan AR(1)-GJR-t(1,1). Ketiadaan autokorelasi pada residual model menunjukkan bahwa residual model AR(1)-GARCH-t(1,1) dan AR(1)-GJR-t(1,1) berdistribusi bebas dan identik (independent identically distributed), disingkat IID. Keadaan residual model yang IID telah memenuhi asumsi yang diperlukan oleh extreme value theory sehingga akan digunakan untuk identifikasi nilai ekstrem pada tahap selanjutnya.
Tabel 3. Uji Ljung-Box dan ARCH-LM Residual Model AR(1)-GARCH-t(1,1) dan AR(1)-GJR-t(1,1)
|
Uji Formal |
р - value Residual Model | |||||
|
AR(1)-GARCH-t(1,1) |
AR(1)-GJR-t(1,1) | |||||
|
AUT |
IRL |
SCH |
AUT |
IRL |
SCH | |
|
Ljung-Box Residual |
0,7910 |
0,6167 |
0,0640 |
0,7689 |
0,5600 |
0,0699 |
|
Kuadrat residual |
0,9644 |
0,7032 |
0,2173 |
0,9327 |
0,6742 |
0,3361 |
|
ARCH-LM Residual |
0,7091 |
0,8635 |
0,3433 |
0,5726 |
0,8460 |
0,6151 |
|
Kuadrat residual |
0,9951 |
0,9995 |
0,9996 |
0,9936 |
0,9979 |
1,0000 |
Di sisi lain, uji ARCH-LM pada residual dan kuadrat residual model menunjukkan р - value lebih besar dari taraf signifikan a = 0,05 sehingga tidak cukup bukti untuk menolak hipotesis nol. Hal ini berarti tidak ada efek ARCH pada residual maupun kuadrat residual model AR(1)-GARCH-t(1,1) dan AR(1)-GJR-t(1,1). Ketiadaaan efek autokorelasi dan efek ARCH pada residual maupun kuadrat residual model menunjukkan bahwa penerapan GARCH-t(1,1) serta GJR-t(1,1) telah dapat mengakomodasi keberadaan autokorelasi dan heteroskedastisitas pada data. Dengan kata lain, model GARCH-t(1,1) dan GJR-t(1,1) telah dapat
memodelkan volatilitas return indeks saham AUT, IRL, dan SCH dengan baik sehingga tidak terdapat lagi efek ARCH dan efek autokorelasi pada residual model. Selain efek autokorelasi dan heteroskedastisitas, return indeks saham AUT, IRL, dan SCH juga memiliki ekor distribusi yang lebih memanjang ke kiri. Ketidaksimetrisan pada ekor distribusi mengindikasikan keberadaan ekor gemuk yang menyebabkan besarnya peluang kejadian ekstrem. Keberadaan ekor gemuk secara grafis dapat pula ditunjukkan oleh plot kuantil-kuantil atau disingkat plot QQ.
Sample Ouantlles Sample Ouantlles
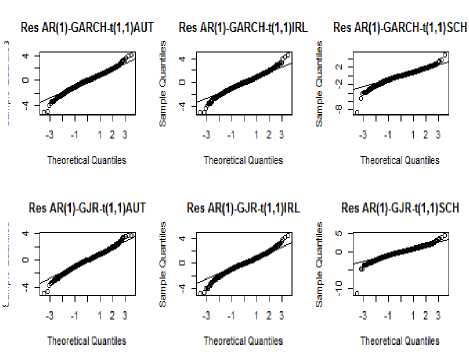
Gambar 1. Plot QQ Kuantil Residual Model AR(1)-GARCH-t(1,1) dan AR(1)-GJR-t(1,1) dengan Distribusi Normal
Plot QQ pada Gambar 1. menunjukkan hubungan antara kuantil residual model AR(1)-GARCH-t(1,1) dan AR(1)-GJR-t(1,1) dengan kuantil distribusi normal standar. Terlihat bahwa titik-titik pada bagian ekor atas maupun ekor bawah distribusi tidak berhimpit atau melenceng dari garis lurus. Hal ini menunjukkan bahwa residual model tidak mengikuti distribusi normal dan memiliki ekor distribusi yang lebih gemuk jika dibandingkan dengan distribusi normal. Keberadaan ekor gemuk pada residual model AR(1)-GARCH-t(1,1) dan AR(1)-GJR-t(1,1) perlu dimodelkan menggunakan teori nilai ekstrem atau extreme value theory disingkat EVT.
Analisis selanjutnya difokuskan pada ekor kiri distribusi karena ekor kiri distribusi mencerminkan nilai ekstrem negatif penyebab risiko investasi. Pemodelan nilai ekstrem pada residual model AR(1)-GARCH-t(1,1) dan AR(1)-GJR-t(1,1) dilakukan menggunakan pendekatan peak over threshold disingkat POT.
Identifikasi nilai ekstrem menggunakan metode peak over threshold diawali dengan penentuan ambang batas atau threshold u. Chaves-Demoulin (1999) dalam Zuhara et al. (2012) menyarankan untuk memilih ambang batas ■u sedemikian hingga data yang berada di atas ambang batas ■u kurang lebih 10 % dari keseluruhan data. Sepuluh persen dari data ekor kiri residual model yang telah terurut dengan urutan naik dimodelkan menggunakan GPD sehingga diperoleh sebanyak 10% ×2289≈ 229 data ekstrem. Pemodelan GPD pada ekor kiri distribusi dilakukan berdasarkan Teorema 1 bahwa fungsi distribusi dari data amatan yang berada di atas ambang batas ■u dapat dihampiri dengan fungsi distribusi GPD.
Estimasi parameter GPD menggunakan maximum likelihood estimator dapat dilihat pada Tabel 4. Nilai positif pada estimasi parameter bentuk ̂ diberikan oleh residual model AR(1)-GARCH-t(1,1) dan AR(1)-GJR-t(1,1) pada indeks saham SCH serta residual AR(1)-GARCH-t(1,1) pada indeks saham AUT. Nilai estimasi parameter bentuk ̂ yang lebih besar dari nol mengindikasikan data amatan di atas threshold ■u memiliki ekor distribusi yang gemuk dan mengikuti distribusi Pareto. Di sisi lain, residual model AR(1)-GARCH-t(1,1) dan AR(1)-GJR-t(1,1) pada indeks saham IRL serta residual AR(1)-GJR-t(1,1) pada indeks saham AUT bernilai negatif. Nilai negatif pada estimasi parameter bentuk ̂ menunjukkan bahwa data amatan di atas threshold ■u mengikuti distribusi Pareto II serta memiliki ekor distribusi yang lebih pendek dibandingkan dengan ekor distribusi indeks saham SCH.
Estimasi parameter GPD pada Tabel 4 digunakan untuk membangkitkan bilangan acak berdistribusi GPD sehingga diperoleh distribusi
Tabel 4. Estimasi Parameter Model GPD Menggunakan MLE
|
Parameter |
AR(1)-GARCH-t(1,1) AR(1)-GJR-t(1,1) AUT IRL SCH AUT IRL SCH |
|
Ambang batas (■u) Data lebihan Param Skala ( ̂) Param Bentuk ( ) |
-1,30122 -1,22439 -1,25146 -1,26574 -1,23084 -1,24725 229 229 229 229 229 229 0,59070 0,66087 0,68978 0,64945 0,65692 0,64035 0,01463 -0,03476 0,03722 -0,06828 -0,04145 0,08802 |
dengan ekor kiri berdistribusi GPD dan distribusi student-t pada bagian lainnya. Residual model marginal dari masing-masing indeks saham selanjutnya digunakan untuk melakukan pemodelan struktur kebergantungan antarindeks saham dalam portofolio menggunakan copula.
Struktur kebergantungan antarindeks saham memberikan informasi mengenai perilaku indeks saham dalam portofolio. Residual model AR(1)-GARCH-t(1,1)-GPD dan AR(1)-GJR-t(1,1)-GPD dari masing-masing indeks saham perlu ditransformasi menjadi distribusi seragam standar (uniform) [0,1] menggunakan probability integral transformation. Hal ini perlu dilakukan karena copula terdefinisi pada domain [0,1]. Plot kontur dan plot pencar data hasil transformasi seragam [0,1] dari residual AR(1)-GARCH-t(1,1)-GPD dan AR(1)-GJR-t(1,1)-GPD diberikan pada Gambar 2.
Transformasi Seragam [0,1] Residual AR(1)-GARCH-t(1,1)-GPD
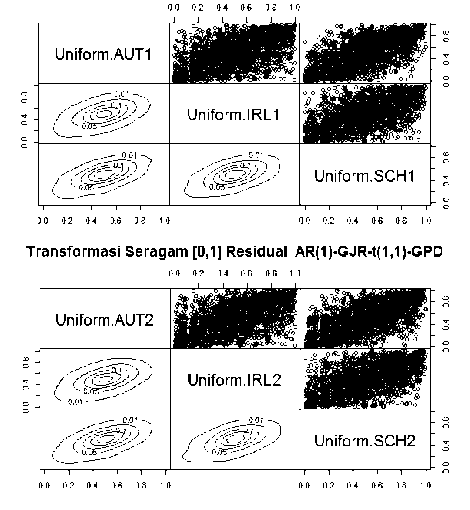
Gambar 2. Plot Kontur dan Plot Pencar Data Transformasi Seragam [0,1] dari Residual AR(1)-GARCH-t(1,1)-GPD dan AR(1)-GJR-t(1,1)-GPD
Gambar 2 menunjukkan titik-titik pada plot pencar data hasil transformasi seragam [0,1] dari residual AR(1)-GARCH-t(1,1)-GPD dan AR(1)-GJR-t(1,1)-GPD yang cenderung mengelompok dibagian tengah. Hal ini mengindikasikan indeks saham AUT, IRL, dan SCH tidak memiliki
kebergantungan pada bagian ekor atas maupun ekor bawah. Ketiadaan dependensi pada bagian ekor semakin diperjelas melalui visualisasi plot kontur yang memperlihatkan garis kontur lebih rapat dibagian tengah.
Data hasil transformasi seragam [0,1] selanjutnya digunakan untuk melakukan segala proses yang berhubungan dengan analisis struktur kebergantungan. Pada kasus trivariat terdapat y = 3 kemungkinan dekomposisi C-vine copula. Pemilihan dekomposisi C-vine copula yang sesuai untuk memodelkan kebergantungan antarindeks saham dalam portofolio dilakukan dengan terlebih dahulu menentukan indeks saham yang bertindak sebagai peubah kunci (root). Peubah kunci dalam hal ini merupakan indeks saham yang berinteraksi dengan seluruh indeks saham lain dalam portofolio. Penentuan peubah kunci dilakukan dengan mempertimbangkan indeks saham yang memiliki nilai kebergantungan paling besar dengan indeks saham lain dalam portofolio. Tabel 5 menunjukkan nilai kebergantungan antarindeks saham menggunakan ukuran kebergantungan Spearman's rho.
Berdasarkan Tabel 5, nilai positif pada Spearman's rho menunjukkan hubungan kebergantungan yang positif antarindeks saham dalam portofolio. Hubungan kebergantungan yang positif mengindikasikan indeks saham AUT, IRL, dan SCH memiliki pergerakan yang searah. Hal ini berarti penurunan nilai return suatu indeks saham akan diikuti oleh penurunan nilai return indeks saham lainnya, begitu pula sebaliknya. Tanda bintang (*) pada Tabel 5 menunjukkan nilai Spearman's rho paling besar yang menyatakan hubungan kebergantungan antarindeks saham tererat dalam portofolio.
Berdasarkan Tabel 5, indeks saham SCH memiliki nilai kebergantungan paling besar dengan indeks saham AUT maupun IRL. Oleh karena itu, indeks saham SCH cukup tepat dijadikan sebagai peubah kunci (root) dalam struktur dekomposisi C-vine copula antarindeks saham dalam portofolio.
Parameter C-vine copula diestimasi menggunakan maximum likelihood estimator (MLE). Hasil estimasi parameter C-vine copula dari data transformasi seragam residual model AR(1)-GARCH-t(1,1)-GPD dan AR(1)-GJR-t(1,1)-GPD berturut-turut diberikan pada Tabel 6 dan Tabel 7.
Berdasarkan Tabel 6 dan Tabel 7, nilai parameter Clayton copula, Gumbel copula, dan Frank copula pada kedua model tidak memperlihatkan perbedaan yang signifikan.
Penentuan jenis copula terbaik dilakukan dengan memilih nilai kriteria Akaike (AIC) dan kriteria Bayes (BIC) terkecil. Frank copula memiliki nilai AIC dan BIC paling kecil pada model AR(1)-GARCH-t(1,1)-GPD maupun AR(1)-GJR-t(1,1)-GPD. Oleh karena itu, jika dibandingkan dengan Clayton dan Gumbel copula maka Frank copula merupakan jenis copula terbaik yang dapat memodelkan kebergantungan antarindeks saham dalam portofolio pada penelitian ini.
Tabel 5. Nilai Spearman's Rho Transformasi Seragam [0,1]
|
Spearman's Rho |
Transformasi Seragam [0,1] Residual Model AR(1)-GARCH-t(1,1)-GPD AR(1)-GJR-t(1,1)-GPD AUT IRL SCH AUT IRL SCH |
|
AUT IRL SCH |
1,000000 0,559903 0,671035* 1,000000 0,554208 0,662607* 0,559903 1,000000 0,595498* 0,554208 1,000000 0,590965* 0,671035 0,595498 1,000000 0,662607 0,590965 1,000000 |
Tabel 6. Estimasi Parameter C-vine Copula dari Transformasi Seragam [0,1] Residual AR(1)-GARCH-t(1,1)-GPD
|
Copula |
Tree |
Edge |
Parameter |
LL |
AIC |
BIC |
|
3,1 |
1,37 (0,04) | |||||
|
Clayton |
3,2 |
1,12 (0,04) |
1060,44 |
-2114,88 |
-2097,67 | |
|
2 |
2,1|3 |
0,25 (0,00) | ||||
|
3,1 |
2,14 (0,07) | |||||
|
Gumbel |
3,2 |
1,92 (0,06) |
1366,17 |
-2726,35 |
-2709,14 | |
|
2 |
2,1|3 |
1,16 (0,00) | ||||
|
3,1 |
6,58 (0,32) | |||||
|
Frank |
3,2 |
5,60 (0,28) |
1395,11 |
-2784,22 |
-2767,01 | |
|
2 |
2,1|3 |
1,82 (0,15) |
Tabel 7. Estimasi Parameter C-vine Copula dari Transformasi Seragam [0,1] Residual AR(1)-GJR-t(1,1)-GPD
|
Copula |
Tree |
Edge |
Parameter |
LL |
AIC |
BIC |
|
3,1 |
1,28 (0,05) | |||||
|
Clayton |
1 |
3,2 |
1,09 (0,04) |
1016,02 |
-2026,03 |
-2008,82 |
|
2 |
2,1|3 |
0,25 (0,00) | ||||
|
3,1 |
2,04 (0,09) | |||||
|
Gumbel |
3,2 |
1,87 (0,08) |
1280,81 |
-2555,61 |
-2538,41 | |
|
2 |
2,1|3 |
1,16 (0,01) | ||||
|
3,1 |
6,25 (0,33) | |||||
|
Frank |
3,2 |
5,41 (0,28) |
1331,18 |
-2660,37 |
-2643,16 | |
|
2 |
2,1|3 |
1,82 (0,15) |
Dalam mengestimasi nilai conditional value at risk (CVaR) portofolio, perlu dilakukan simulasi return pada masing-masing indeks saham penyusun portofolio yang selanjutnya digunakan untuk membentuk return portofolio. Sebelum melakukan simulasi return, dilakukan penentuan bobot masing-masing indeks saham penyusun portofolio tersebut. Bobot atau proporsi dana yang digunakan yaitu sebesar 1⁄ pada masing-masing indeks saham penyusun portofolio. Setelah memperoleh return portofolio, hal lain yang perlu ditentukan sebelum mengestimasi nilai CVaR portofolio yaitu menentukan tingkat kepercayaan serta periode holding. Tingkat kepercayaan yang digunakan pada penelitian ini yaitu sebesar 90%, 95%, dan 99%. Di sisi lain, periode holding atau lama investor untuk tetap menahan atau memegang investasi diasumsikan satu hari.
CVaR merupakan ukuran risiko yang memperhitungkan besarnya kerugian melebihi nilai VaR. Oleh karena itu, sebelum
mengestimasi nilai CVaR portofolio, terlebih dahulu perlu dihitung nilai VaR portofolio. Tabel 8 menyajikan nilai VaR dan CVaR harian menggunakan model EVT-GARCH-vine copula dan EVT-GJR-vine copula. Misalkan dengan menginvestasikan modal sebesar $1.000.000, maka nilai kerugian maksimum yang mungkin dialami investor satu hari ke depan pada tingkat kepercayaan 90 % menggunakan Clayton copula dengan metode EVT-GJR-vine copula yaitu sebesar 2,7345% × $1.000.000 = $27.345 sedangkan dengan metode EVT-GARCH-vine copula yaitu sebesar 3,0339% × $1.000.000 = $30.339. Interpretasi serupa berlaku pula untuk jenis copula lainnya.
Nilai VaR dan CVaR pada Tabel 8 selanjutnya digunakan untuk mengetahui perbandingan kinerja metode EVT-GARCH-vine copula dan EVT-GJR-vine copula dalam mengestimasi CVaR portofolio menggunakan backtesting.
Tabel 8. Estimasi Value at Risk dan Conditional Value at Risk Model EVT-GARCH-Vine
Copula dan EVT-GJR-Vine Copula
Value at Risk
|
Copula |
Tingkat Kepercayaan |
Conditional Value at Risk (dalam %) | |
|
EVT-GARCH-Vine EVT-GJR-Vine | |||
|
Copula |
Copula | ||
|
90 % |
1,7627 |
1,5522 | |
|
3,0339 |
2,7345 | ||
|
Clayton |
95 % |
2,5889 3,9338 |
2,3282 3,5689 |
|
99 % |
4,9157 |
4,0692 | |
|
6,0349 |
5,9866 | ||
|
90 % |
1,7384 |
1,6032 | |
|
2,8394 |
2,5909 | ||
|
Gumbel |
95 % |
2,4273 |
2,2408 |
|
3,6379 |
3,3317 | ||
|
99 % |
4,3699 |
3,6313 | |
|
5,4850 |
5,3966 | ||
|
90 % |
1,8291 |
1,6515 | |
|
2,9138 |
2,6485 | ||
|
Frank |
95 % |
2,5543 |
2,2872 |
|
3,6902 |
3,3644 | ||
|
99 % |
4,3870 |
3,7858 | |
|
5,5442 |
5,4134 | ||
Tabel 9. Nilai Statistik ^l , ^2 , dan V untuk Backtesting Conditional Value at Risk
V1
|
Tingkat |
V2 | ||
|
Copula |
Kepercayaan pada |
V | |
|
CVaR |
EVT-GARCH-Vine |
EVT-GJR-Vine | |
|
Copula |
Copula | ||
|
0,003910345 |
0,002950183 | ||
|
90 % |
0,009117195 |
0,006123463 | |
|
0,006513770 |
0,004536823 | ||
|
-0,006219807 |
-0,003906699 | ||
|
Clayton |
95 % |
0,018116146 |
0,014466847 |
|
0,012167977 |
0,009186773 | ||
|
-0,002972855 |
0,004083060 | ||
|
99 % |
0,039127265 |
0,038644800 | |
|
0,021050060 |
0,021363930 | ||
|
0,001965095 |
0,0003765701 | ||
|
90 % |
0,007171945 |
0,0046875065 | |
|
0,004568520 |
0,0025320383 | ||
|
-0,003215737 |
-0,006421112 | ||
|
Gumbel |
95 % |
0,015157810 |
0,011952434 |
|
0,009186773 |
0,009186773 | ||
|
-0,008471319 |
-0,001816979 | ||
|
99 % |
0,033628801 |
0,032744758 | |
|
0,021050060 |
0,017280868 | ||
|
0,001810910 |
0,00005661807 | ||
|
90 % |
0,007916761 |
0,005263468 | |
|
0,004863836 |
0,002660043 | ||
|
-0,008655152 |
-0,005951614 | ||
|
Frank |
95 % |
0,015680802 |
0,012421933 |
|
0,012167977 |
0,009186773 | ||
|
-0,007879545 |
-0,001648929 | ||
|
99 % |
0,034220575 |
0,032912807 | |
|
0,021050060 |
0,017280868 |
Backtesting model CVaR merupakan suatu prosedur untuk membandingkan nilai estimasi CVaR dengan data return historis sehingga dapat disimpulkan kinerja suatu model CVaR dalam mengestimasi risiko portofolio. Metode backtesting CVaR yang digunakan pada penelitian ini yaitu V-test. Terdapat dua ukuran pada V-test yaitu V1 dan V2 . Adapun kombinasi dari kedua ukuran tersebut yaitu nilai statistik V. Nilai statistik V1 , K2, dan V dari metode EVT-GARCH-vine copula dan EVT-GJR-vine copula dapat dilihat pada Tabel 9. Untuk menilai kinerja suatu model, maka nilai statistik V1 dan ^2 yang diperoleh pada Tabel 9 harus dimutlakkan terlebih dahulu. Apabila suatu model memiliki kinerja yang baik, maka harga mutlak dari V1 dan ^2 memiliki nilai yang kecil. Oleh karena statistik V merupakan kombinasi dari ukuran V1
dan ^2 , maka nilai statistik V yang kecil juga mengindikasikan bahwa model tersebut memiliki kinerja yang baik dalam mengestimasi CVaR portofolio.
Berdasarkan Tabel 9, sebagian besar nilai statistik ^l , ½2 , dan V pada metode EVT-GJR-vine copula memiliki nilai yang lebih kecil dibandingkan dengan nilai statistik V1 , ^2 , dan V pada metode EVT-GARCH-vine copula. Hal ini menunjukkan bahwa metode EVT-GJR-vine copula memiliki kinerja yang lebih baik apabila dibandingkan dengan metode EVT-GARCH-vine copula dalam mengestimasi nilai CVaR portofolio pada studi kasus ini.
Berdasarkan uraian hasil dan pembahasan, disimpulkan bahwa pada studi kasus ini metode EVT-GJR-vine copula memiliki kinerja yang lebih baik apabila dibandingkan dengan metode EVT-GARCH-vine copula dalam mengestimasi nilai CVaR portofolio yang terdiri atas indeks saham FTSE Austria (AUT), FTSE Ireland (IRL), dan FTSE Switzerland (SCH). Hal ini berdasarkan nilai statistik V 1 , ^2 , dan V pada metode EVT-GJR-vine copula yang secara
DAFTAR PUSTAKA
Aas, K., Czado, C., Frigessi, A., & Bakken, H.
(2009). Pair Copula Constructions of Multiple Dependence. Insurance, Mathematics, and Economics, 44, 182-198.
Brooks, C. (2008). Introductory Econometrics for Finance . Cambridge: Cambridge University Press.
Danielsson, J. (2011). Financial Risk
Forecasting: The Theory and Practice of
Forecasting Market Risk with
Implementation in R and Matlab. Chichester: John Wiley & Sons, Ltd.
Dharmawan, K. (2015). Estimasi Nilai AVaR
Menggunakan Model GJR dan Model
GARCH. Jurnal Matematika, 5(2), 117-127.
Embrechts, P., Kaufmann, R., & Patie, P. (2005).
Strategic Long-Term Financial Risks: Single
Risk Factors. Computational Optimization and Applications, 32, 61-90.
Franke, J., Härdle, W. K., & Hafner, C. M.
(2011). Statistics of Financial Markets: An
Introduction. Third Edition. London: Springer-Verlag Berlin Heidelberg.
Huang, S.-C., Chien, Y.-H., & Wang, R.-C.
(2011). Applying GARCH-EVT-Copula
Models for Portfolio Value at Risk on G7 Currency Markets. International Research Journal of Finance and Economics(74), 136151.
Investing, [online]. Available at: http://www.
investing.com/indices/global-indices?major
Indices=on&r_id=3 terakhir diakses 22 September 2018.
Klugman, S. A., Panjer, H. H., & E.Willmot, G.
(2008). Loss Models from Data to Decisions.
Third Edition. Canada: John Wiley & Sons, Inc.
umum lebih kecil daripada nilai statistik V1, ^2 , dan V dari metode EVT-GARCH-vine copula.
Pemilihan struktur dekomposisi pada penelitian ini hanya melibatkan variasi struktur dekomposisi dari keluarga C-vine. Pada penelitian selanjutnya diharapkan dapat melibatkan struktur dekomposisi dari keluarga D-vine dan reguler vine secara umum serta melibatkan copula bivariat dengan jenis yang lebih beragam.
Kurowicka, D., & Cooke, R. (2006). Uncertainty Analysis with High Dimensional Dependence Modelling. Chichester: John Wiley & Sons Ltd.
McNeil, A. J., & Frey, R. (2000). Estimation of Tail-Related Risk Measures for Heteroscedastic Financial Time Series: An Extreme Value Approach. Journal of Empirical Finance, 7(3), 271–300.
McNeil, A. J., Frey, R., & Embrechts, P. (2005). Quantitative Risk Management: Concepts, Techniques and Tools. Princeton: Princeton University Press.
Sumarjaya, I. W. (2013). Memodelkan Ketergantungan dengan Kopula. Jurnal Matematika, 3(1), 34-42.
Tsay, R. S. (2002). Analysis of Financial Time Series Financial Econometrics. Chicago: John Wiley & Sons, Inc.
Yamai, Y., & Yoshiba, T. (2005). Value at Risk Versus Expected Shortfall: A Practical Perspective. Journal of Banking & Finance, 29, 997–1015.
Zivot, E. (2008). Practical Issues in the Analysis of Univariate GARCH Models. Seattle: Department of Economics University of Washington.
Zuhara, U., Akbar, M. S., & Haryono. (2012). Penggunaan Metode VaR (Value at Risk) dalam Analisis Risiko Investasi Saham dengan Pendekatan Generalized Pareto Distribution (GPD). Jurnal Sains dan Seni ITS, 1(1), 56-61.
26
Discussion and feedback