ANALISIS STABILITAS HASIL GENOTIPE JAGUNG MENGGUNAKAN METODE FIXED AMMI
on
E-Jurnal Matematika Vol. 8(1), Januari 2019, pp. 9-14
DOI: https://doi.org/10.24843/MTK.2019.v08.i01.p229
ISSN: 2303-1751
ANALISIS STABILITAS HASIL GENOTIPE JAGUNG MENGGUNAKAN METODE FIXED AMMI
Modana Lolita1§, I Komang Gde Sukarsa2, Made Susilawati3
1Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email:modanalolita8@gmail.com]
2Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email:sukarsakomang@yahoo.com]
3Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: mdsusilawati@unud.ac.id]
§Corresponding Author
ABSTRACT
Additive Main Effect and Multiplicative Interaction (AMMI) is a method that is used in research to study interaction between genotype and location. The aim of this research is to apply fixed AMMI in examining the production of corn genotype data and to explore yield stability of its based on biplot picture and AMMI Stability Value (ASV). This research uses six corn genotypes, eight trial locations, and three repetitions. The Interaction Principal Component Analysis (IPCA) that are significant to entered in the model based on analysis of variance fixed AMMI are IPCA1, IPCA2, and IPCA3 with total diversity interaction as much as 92,16%. The biplot picture and ASV should the stable genotype in all location are genotype KUI Carotenoid Syn FS. 17-3-2-B-B × T01 and genotype CML 305-B-B × T01. In addition, corns that are able to adapt only in certain location is: genotype KUI Carotenoid Syn FS. 5-1-5-B-B × T01, genotype KUI Carotenoid Syn FS. 25-3-2-B-B × T01, genotype KUI Carotenoid Syn FS. 17-3-1-B × T01, and genotype CML 130-B-B × T01.
Keywords: AMMI, Biplot, Fixed AMMI, Stability
pengulangan biasa atau rancangan acak lengkap (RAL) maupun sebagai kelompok atau rancangan acak kelompok (RAK). Apabila ada pengaruh interaksi, uji lanjut yang digunakan dalam analisis ragam adalah uji perbandingan berganda. Namun uji tersebut tidak cukup untuk mendeteksi stabilitas suatu genotipe sehingga diperlukan metode lain untuk melihat stabilitas tersebut. Salah satu metode yang digunakan adalah additive main effect and multiplicative interaction (AMMI).
AMMI merupakan metode yang digunakan peneliti untuk mengamati interaksi antara genotipe dengan lokasi. Interaksi genotipe dengan lokasi (IGL) adalah perubahan keragaman dari dua atau beberapa genotipe pada beberapa lokasi yang berbeda (Mattjik & Sumertajaya, 2000).
Menurut Mattjik, et al (2011) model AMMI pada dasarnya adalah model dengan faktor tetap (fixed model). Jika diasumsikan genotipe
dan lokasi ditentukan secara subjektif oleh peneliti dan kesimpulan hanya terbatas pada genotipe dan lokasi yang dicobakan, maka analisis AMMI yang digunakan adalah model AMMI tetap (fixed AMMI). Analisis stabilitas AMMI dapat lihat melalui gambaran biplot AMMI dan indeks stabilitas AMMI (ISA).
Penelitian ini menggunakan data enam genotipe jagung, delapan lokasi percobaan, dan tiga ulangan. Tujuan dari penelitian ini adalah menentukan hasil analisiss data genotipe jagung menggunakan metode fixed AMMI dan menentukan stabilitas enam genotipe jagung berdasarkan gambaran biplot dan ISA.
Model linear percobaan multilokasi dengan fixed AMMI secara lengkap dapat ditulis sebagai berikut:
Yger = + ag + βe +∑k=ι √ ^kΨgkPek + ^ge + Zger (1)
dengan:
g=1,2,…,a;e=1,2,…,b;r=1,2,…,m.
Yger menyatakan nilai pengamatan pada genotipe k- g , lokasi ke-e , dan ulangan ke-r,P menyatakan nilai tengah (rataan umum), ag menyatakan pengaruh utama genotipe ke- g terhadap respon yang diamati, βe menyatakan pengaruh utama lokasi ke-e terhadap respon yang diamati, √λn menyatakan nilai singular komponen bilinear ke-n, Φgrι menyatakan pengaruh ganda genotipe ke-g melalui komponen bilinear ke-n, Pen menyatakan pengaruh ganda lokasi ke-e melalui komponen bilinear ke-Il , ^ge menyatakan galat dari pemodelan bilinear, Zger menyatakan pengaruh acak galat faktor tetap genotipe ke- g , faktor tetap lokasi ke- e, ulangan ke-r, (Zegr N (0, σε2)).
Penentuan banyaknya komponen utama interaksi (KUI) yang dapat masuk ke dalam model dapat ditentukan melalui penguraian nilai singular matriks interaksiZ . Penguraian nilai singular untuk matriks Z dapat dimodelkan sebagai berikut:
Z=USAT (2)
matriks U dan A merupakan matriks dengan
kolom orthonormal, dan matriks S merupakan matriks diagonal dengan elemen diagonalnya merupakan akar kuadrat nilai eigen positif bukan nol. Unsur-unsur diagonal dari matriks S disebut nilai singular matriks Z (Jolliffe, 2002).
Pada biplot AMMI kontur ellips yang digunakan diperoleh dari perhitungan jari-jari ellips. Apabila suatu genotipe berada didalam kontur maka dapat dikatakan bahwa genotipe tersebut stabil. Sedangkan jika genotipe berada di luar kontur maka genotipe tersebut dapat dikategorikan sebagai genotipe yang tidak stabil atau dapat dikatakan bahwa genotipe stabil pada lokasi tertentu. Persamaan yang digunakan untuk mendapatkan jari-jari elips (Mattjik, et al., 2011) adalah:
n=± ⅛ √( (( n-p )) ^ .n-p( : )) (3)
dengan:
ri menyatakan panjang jari-jari; i=1 untuk jari-jari panjang; i=2 untuk jari-jari pendek, n menyatakan banyaknya pengamatan (genotipe + lokasi), P menyatakan banyaknya peubah, ⅛ menyatakan nilai singular, . (a)
menyatakan nilai sebaran F dengan derajat bebas pertama (db1) dan derajat bebas kedua (db2) berturut-turut adalah P dan n-P , dengan nilai alpha yang digunakan adalah a=5%.
Untuk mempermudah melihat tingkat stabilitas suatu genotipe terhadap lokasi digunakan indeks stabilitas. Penentuan indeks stabilitas genotipe ditentukan oleh skor KUI1 dan skor KUI2 dari masing-masing genotipe (Mattjik, et al., 2011). ISA didefinisikan
sebagai berikut:
ISA = √[^(nilai KUI1)] +(nilai KUI2 )2 (4)
y U22 J
Indeks dibangun berdasarkan konsep jarak, semakin besar indeks stabilitas suatu genotipe, semakin jauh pula jarak genotipe dari titik pusat sumbu koordinat sehingga genotipe tersebut semakin tidak stabil, begitu pula sebaliknya.
-
2. METODE PENELITIAN
Jenis data yang digunakan dalam penelitian ini adalah data sekunder yang diperoleh dari Yasin, et al (2014). Data sekunder yang digunakan berupa data hasil biji genotipe jagung fungsional dengan percobaan enam perlakuan genotipe, delapan lokasi, dan tiga ulangan pada musim hujan tahun 2010. Berikut merupakan tabel kode nama genotipe dan lokasi percobaan:
Tabel 1. Genotipe Jagung
|
Genotipe |
Kode |
|
CML 130-B-B × T01 |
G1 |
|
KUI Carotenoid Syn FS. 17-3-2-B-B × T01 |
G2 |
|
CML 305-B-B × T01 |
G3 |
|
KUI Carotenoid Syn FS. 5-1-5-B-B × T01 |
G4 |
|
KUI Carotenoid Syn FS. 17-3-1-B × T01 |
G5 |
|
KUI Carotenoid Syn FS. 25-3-2-B-B × T01 |
G6 |
Tabel 2. Lokasi Percobaan
|
Lokasi |
Kode |
|
Kebun Percobaan Maros |
E1 |
|
Kebun Percobaan Bajeng |
E2 |
|
Kabupaten Polman |
E3 |
|
Kabupaten Donggala |
E4 |
|
Kebun Percobaan Pandu |
E5 |
|
Kebun Percobaan Muneng |
E6 |
|
Lombok Timur |
E7 |
|
Kebun Percobaan Sebapo |
E8 |
Tahapan analisis dalam penelitian ini adalah: (1) menganalisis data pada analisis ragam percobaan genotipe jagung pada berbagai lokasi dengan analisis ragam dua faktor RAKL. (2) membentuk matriks data berukuran 6 × 8. Entri-entri matriks tersebut merupakan data rata-rata dari hasil enam genotipe jagung di delapan lokasi berbeda. (3) menguraikan nilai SVD berdasarkan konsep Analisis Komponen Utama. (4) analisis ragam model fixed AMMI. (5) menghitung kontribusi masing-masing nilai KUI. (6) menghitung indeks stabilitas AMMI. (7) menginter-
pretasikan kestabilan genotipe berdasarkan hasil biplot AMMI2 dan indeks stabilitas AMMI.
-
3. HASIL DAN PEMBAHASAN
Pengujian analisis ragam dilakukan untuk melihat apakah ada pengaruh interaksi genotipe dengan lokasi. Berikut merupakan hasil analisis ragam data pengamatan sebelum dilanjutkan dengan analisis AMMI.
Tabel 3. Analisis Ragam Produksi Jagung
|
Sumber Keragaman |
db |
JK |
KT |
Fhltung |
F tab e 1 |
|
Genotipe |
5 |
123,61 |
24,72 |
44,95* |
2,311 |
|
Lokasi |
7 |
176,49 |
25,21 |
45,84* |
2,109 |
|
Interaksi |
35 |
76,19 |
2,17 |
3,96* |
1,548 |
|
Kelompok |
2 |
0,04 |
0,02 |
0,04 |
3,093 |
|
Galat |
94 |
51,72 |
0,55 | ||
|
Total |
143 |
428,05 |
Keterangan: *) Signifikan
Hasil analisis ragam untuk interaksi produksi jagung dari enam genotipe jagung pada delapan lokasi di atas menunjukan bahwa pengaruh utama (genotipe dan lokasi) dan pengaruh interaksi antara genotipe dengan lokasi berpengaruh nyata karena Fhitung > Ftabel.
Hasil penguraian nilai singular diperoleh enam nilai singular tak nol, yaitu 3,661032; 2,502181; 1,937493; 1,378454; 0,3039594; 2,426457× 10 -1 5. Berdasarkan nilai singular tersebut terlihat bahwa banyaknya KUI yang dapat dipertimbangkan untuk model fixed AMMI adalah komponen pertama sampai keenam. Diperoleh pula enam nilai eigen yaitu A1 = 13,40316; A2 = 6,260912; A3 = 3,753880; A4 = 1,900135; A5 = 0,09239132; A6 = 5,887693× 10 ^3 0.
Dari penguraian nilai singular dengan memperoleh enam nilai eigen, kemudian dilakukan kembali perhitungan analisis ragam model fixed AMMI. Analisis ragam model fixed
AMMI ini memperlihatkan skor KUI yang signifikan dan dapat masuk ke dalam model
Tabel 4. Analisis Ragam Data Hasil Produksi Jagung dengan Fixed AMMI
|
Sumber Keragaman |
db |
JK |
KT |
Fhitung |
Ftabel |
|
Genotipe |
5 |
123,61 |
24,722 |
44,95 |
2,311 |
|
Lokasi |
7 |
176,49 |
25,213 |
45,84 |
2,109 |
|
Interaksi |
35 |
76,19 |
2,177 |
3,96 |
1,548 |
|
KUI1 |
11 |
40,21 |
3,66 |
6,65* |
1,891 |
|
KUI2 |
9 |
18,78 |
2,09 |
3,80* |
1,981 |
|
KUI3 |
7 |
11,26 |
1,61 |
2,93* |
2,109 |
|
KUI4 |
5 |
5,70 |
0,32 |
0,58 |
2,311 |
|
KUI5 |
3 |
0,28 |
0,09 |
0,16 |
2,701 |
|
Kelompok |
2 |
0,04 |
0,02 |
0,04 |
3,093 |
|
Galat |
94 |
51,725 |
0,55 | ||
|
Total |
143 |
428,055 |
Keterangan: *) Signifikan
Dengan membandingkan nilai Fhitung dan Ftabel dapat dilihat pada Tabel 4 bahwa nilai Fhitung KUI1, KUI2, dan KUI3 lebih besar dari pada nilai Ftabel. Dengan demikian keputusan adalah tolak H0. Hal ini berarti KUI1, KUI2, dan KUI3 berpengaruh terhadap daya hasil produksi jagung, sehingga daya hasil dapat diterangkan dengan menggunakan fixed AMMI model AMMI3.
Penentuan nilai KUI yang dapat masuk dalam model dapat dilakukan dengan menghitung nilai kontribusi masing-masing KUI. Kontribusi masing-masing KUI adalah KUI1 sebesar 52,75%; KUI2 sebesar 24,64%; KUI3 sebesar 14,77%; KUI4 sebesar 7,48%; KUI5 sebesar 0,36%; dan KUI6 sebesar 0%. Berdasarkan analisis ragam model fixed AMMI dan kontribusi masing-masing KUI dapat dilihat bahwa KUI yang dapat masuk ke dalam model adalah KUI1, KUI2, dan KUI3. Ketiga komponen utama tersebut mampu memberikan keragaman total produksi tanaman jagung sebesar 52,75% + 24,64% + 14,77% = 92,16% yaitu suatu tingkat keragaman yang tinggi. Penentuan stabilitas genotipe digunakan skor KUI1 dan
skor KUI2, sehingga dari dua KUI yang digunakan kontribusi keragaman yang diberikan sudah cukup tinggi yaitu sebesar 52,75% + 24,64% = 77,39%. Menurut Trisnayanti, et al (2015), hal ini sudah melebihi dari 50% atau sudah cukup untuk dapat menentukan stabilitas genotipe.
Biplot AMMI2 dari analisis AMMI dapat digunakan untuk melihat genotipe-genotipe yang stabil pada seluruh lokasi percobaan. Dalam membantu melihat genotipe-genotipe yang stabil digunakan daerah kepercayaan elips pada biplot dengan titik pusat (0,0). Penentuan stabilitas genotipe digunakan dua nilai KUI dengan keragaman terbesar pertama dan kedua, hal ini dikarenakan gambaran biplot hanya terbatas pada dua dimensi. Kontribusi keragaman yang diberikan dari dua nilai KUI yang digunakan cukup tinggi yaitu sebesar 77,39%. Menurut Trisnayanti, et al (2015), hal ini sudah melebihi 50% atau sudah lebih dari cukup untuk dapat menentukan stabilitas genotipe.
Hasil plot Gambar 1 menggambarkan keragaman interaksi sebesar 77,39% dengan masing-masing nilai KUI1 sebesar 52,75% dan KUI2 sebesar 24,64%. Kontur yang terbentuk sebagai daerah keper-cayaan berbentuk elips.
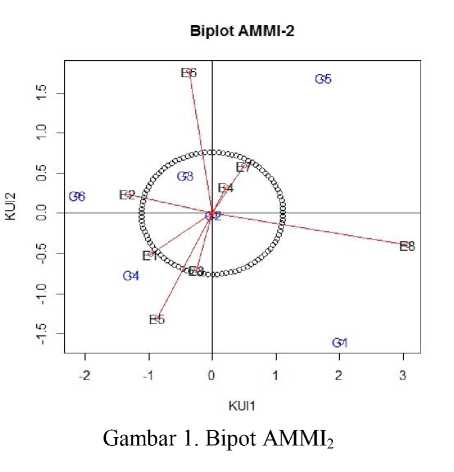
Konsep kestabilan juga ditunjukan dari ISA yang melihat posisi relative genotipe terhadap
titik pusat biplot AMMI2. Hasil perhitungan ISA dapat dilihat pada Tabel 5. Hasil ISA untuk masing-masing genotipe kemudian diurutkan berdasarkan peringkat dari genotipe dengan indeks terkecil hingga genotipe dengan indeks terbesar.
Berdasarkan gambar biplot AMMI2 dan ISA dapat diduga bahwa genotipe yang stabil untuk seluruh lokasi percobaan adalah genotipe yang berada di dalam area kontur dan memiliki jarak yang dekat dengan titik pusat (0,0). Genotipe-genotipe yang dikategorikan stabil pada seluruh lokasi percobaan bila berdasarkan biplot AMMI2 dan ISA adalah G2 dengan jarak
Tabel 5. Indeks Stabilitas AMMI (ISA)
|
Genotipe |
ISA |
Peringkat |
|
G1 |
1,63 |
6 |
|
G2 |
0,02 |
1* |
|
G3 |
0,40 |
2 |
|
G4 |
0,93 |
3 |
|
G5 |
1,53 |
5 |
|
G6 |
1,34 |
4 |
Keterangan : *) genotipe paling stabil
sebesar 0,02 yang berada pada peringkat pertama dan G3 dengan jarak 0,04. Sedangkan untuk genotipe yang tidak stabil atau genotipe yang hanya mampu beradaptasi pada suatu lingkungan tertentu adalah genotipe yang berada di luar area kontur dan memiliki jarak yang jauh dengan titik pusat (0,0). Genotipe-genotipe yang dikategorikan sebagai genotipe yang hanya mampu beradaptasi pada suatu lingkungan tertentu adalah G4, G6, G5, dan G1 dengan masing-masing memiliki jarak terhadap titik pusat (0,0) sebesar 0,93; 1,34; 1,53; 1,63. Genotipe-genotipe yang hanya mampu beradaptasi pada suatu lokasi tertentu dapat dilihat berdasarkan korelasi antar peubah. Jika sudut di antara dua vektor peubah kecil, maka korelasi di antara dua peubah tersebut cenderung besar. Genotipe-genotipe yang mampu beradaptasi pada lokasi tertentu dapat dilihat pada Tabel 6.
Tabel 6. Klasifikasi Genotipe
|
Genotipe |
Lokasi |
|
G4 |
Kebun Percobaan Maros, Kabupaten Polman, dan Kebun Percobaan Pandu |
|
G6 |
Kebun Percobaan Bajeng dan Kebun Percobaan Muneng |
|
G5 |
Kabupaten Donggala dan Lombok Timur |
|
G1 |
Kebun Percobaan Sebapo |
Berdasarkan pembahasan tersebut, dapat disimpulkan bahwa model fixed AMMI pada pada data hasil enam genotipe jagung di delapan lokasi dan tiga ulangan diperoleh tiga komponen utama interaksi yang signifikan dengan total keragaman 92,16%.
Penentuan kestabilan genotipe dengan menggunakan biplot AMMI2 dengan keragaman interaksi sebesar 77,39% dan ISA diperoleh genotipe-genotipe yang dikategorikan mampu memberikan hasil yang baik pada seluruh lokasi percobaan adalah KUI Carotenoid Syn FS. 17-3-2-B-B x T01 dan CML 305-B-B x T01. Sedangkan KUI Carotenoid Syn FS. 5-1-5-B-B x T01 mampu memberikan hasil yang baik apabila ditanam di Kebun Percobaan Maros, Kabupaten Polman, dan Kebun Percobaan Pandu. KUI Carotenoid Syn FS. 25-3-2-B-B x T01 mampu memberikan hasil yang baik apabila ditanam di Kebun Percobaan Bajeng dan Kebun Percobaan Muneng. KUI Carotenoid Syn FS. 17-3-1-B x T01 mampu memberikan hasil yang baik apabila ditanam di Kabupaten Donggala dan Lombok Timur. CML 130-B-B x T01 mampu memberikan hasil yang baik apabila ditanam di Kebun Percobaan Sebapo.
Sebagai saran bagi pembaca yang tertarik dengan topik ini dapat membahas mengenai Mixed AMMI, Generalized Linear Model AMMI (GLM-AMMI), dan Expectation Maximitation AMMI (EM-AMMI).
DAFTAR PUSTAKA
Gomez, K. A & Gomez, A. A. (1995). Prosedur Statistik untuk Penelitian Pertanian. (Edisi ke-2).Terjemahan oleh Sjamsudin dan Baharsjah. Jakarta: UI-Press.
Jolliffe, I. (2002). Principal Component Analysis. (Second Edition). New York: Springer.
Mattjik, A. A., & Sumertajaya, I. M. (2000). Perancangan Percobaan dengan Aplikasi SAS dan Minitab. Bogor: IPB Press.
Mattjik, A. A., Sumertajaya, I. M., Hadi, A. F., & Wibawa, G. N. A. (2011). Pemodelan Additive Main-Effect and Multiplicative Interaction (AMMI): Kini dan yang Akan Datang. Bogor: IPB Press.
Trisnayanti, N. P. A. D., Suciptawati, N. P., & Sukarsa, I.G. (2015). Implementasi Metode Bootstrap dalam Inferensi Titik-Titik Biplot AMMI Model AMMI Campuran (Mixed AMMI). Jurnal Matematika, 4, 115-121.
Yasin HG, M., Sumarno., & Nur. A. (2014). Perakitan Varietas Unggul Jagung Fungsional. Bogor: Badan Penelitian dan Pengembangan Pertanian.
14
Discussion and feedback