APLIKASI REGRESI COX PROPORTIONAL HAZARD PADA SINTASAN PASIEN DIABETES MELITUS
on
E-Jurnal Matematika Vol. 7(3), Agustus 2018, pp. 278-285
DOI: https://doi.org/10.24843/MTK.2018.v07.i03.p215
ISSN: 2303-1751
APLIKASI REGRESI COX PROPORTIONAL HAZARD PADA SINTASAN PASIEN DIABETES MELITUS
Ida Ayu Putu Ratna Dewi1§, Ni Luh Putu Suciptawati2, Ni Ketut Tari Tastrawati3
1Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: dayu.ratna14@gmail.com]
2Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: suciptawati@unud.ac.id]
3Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: tastrawati@unud.ac.id]
§Corresponding Author
ABSTRACT
Diabetes melitus is one of the deadliest diseases in the world. Until now, the incidence and the mortality rate due to diabetes melitus is still very high. To determine the survival of diabetes melitus patients, the significant factors that affect must be obtained by applying Cox Proportional Hazard regression method. The purpose of this study is to determine the chances of probability of diabetes melitus patients and to determine the significant factors that affect on the survival of diabetes melitus patients. The variables used in this study are the length of time of inpatient of diabetes melitus patient in RSUD Wangaya as dependent variable, while age, gender, genetic, blood glucose status, accompanying disease, pain, diabetes drug and insulin, and body mass index as independent variable. Through the analysis of this study we obtained the significant factors that affect the survival of diabetes melitus patients are sex, blood glucose status, and accompanying diseases.
Keywords: Cox Proportional Hazard, Diabetes Melitus, Survival.
faktor-faktor yang memengaruhi lama waktu sintasan hidup pasien diabetes melitus, dalam hal ini menggunakan metode statistika yaitu analisis sintasan (survival analysis). Analisis sintasan adalah analisis data yang berhubungan dengan waktu, mulai dari awal sampai terjadinya suatu peristiwa khusus (Collett, 1994). Perbedaan analisis sintasan dengan analisis statistika yang lain terletak pada konsep data tersensor. Data tersensor adalah data informasi mengenai waktu sintasan individu tetapi tidak diketahui secara pasti berapa lama waktu sintasannya (Kleinbaum & Klein, 2005). Data tersensor yang akan digunakan dalam penelitian ini adalah tersensor interval. Data tersensor interval merupakan sensor yang waktu terjadinya berada dalam suatu selang waktu tertentu yaitu antara selang waktu a dan waktu b (Lee & Wang, 2003).
Analisis sintasan memiliki beberapa tujuan, antara lain tujuan pertama adalah mengestimasi dan menginterpretasi peluang individu
mengalami kejadian sesaat yang dinyatakan dalam bentuk fungsi hazard dan peluang suatu individu mengalami kejadian setelah atau pada suatu titik waktu yang dinyatakan dalam bentuk fungsi sintasan dari suatu data waktu sintasan dan tujuan kedua adalah mengetahui hubungan antara waktu sintasan dengan variabel-variabel yang diduga memengaruhi waktu sintasan. Berdasarkan tujuan pertama analisis sintasan, metode yang berkaitan adalah Kaplan-Meier. Metode Kaplan-Meier merupakan metode nonparametrik yang digunakan apabila data tidak mengikuti suatu distribusi tertentu. Tujuan menggunakan metode Kaplan-Meier dengan menduga fungsi sintasan, fungsi hazard, dan median waktu sintasan untuk memperoleh peluang sintasan hidup suatu individu.
Analisis data yang digunakan pada data sintasan umumnya menggunakan regresi Cox atau dikenal dengan nama Cox proportional hazard. Berdasarkan tujuan kedua analisis sintasan, metode yang berkaitan adalah regresi Cox proportional hazard. Analisis regresi ini mengansumsikan bahwa rasio dari nilai fungsi hazard harus konstan. Secara umum, model regresi Cox dihadapkan pada situasi dimana kemungkinan kegagalan individu bertahan hidup pada suatu waktu yang dipengaruhi oleh satu atau lebih variabel bebas (Collett, 1994). Model Regresi Cox proportional hazard ini dapat digunakan untuk mengetahui hubungan antara waktu sintasan individu dengan variabel yang diduga memengaruhinya (Lee & Wang, 2003). Ketika model regresi Cox proportional hazard diterapkan pada data sintasan, hal yang harus dipenuhi adalah bahwa data yang digunakan harus memenuhi asumsi proportional hazard. Pengecekan asumsi proportional hazard dapat dilakukan dengan pendekatan secara grafik yaitu menggunakan plot log minus log. Dengan demikian, model regresi Cox proportional hazard ini digunakan untuk menentukan model terbaik pada waktu sintasan suatu individu dengan variabel yang diduga memengaruhinya. Penentuan model terbaik ini digunakan metode backward elimination. Cara kerja metode backward
elimination adalah dengan mengeluarkan satu persatu variabel bebas yang tidak signifikan dan dilakukan secara terus-menerus sampai tidak ada variabel bebas yang tidak signifikan.
Penelitian tentang sintasan hidup pasien diabetes melitus telah dilakukan sebelumnya oleh Rahayu, et al. (2012). Penelitian tersebut menyimpulkan bahwa faktor-faktor yang paling berpengaruh pada sintasan hidup pasien diabetes melitus adalah faktor usia, genetik, dan diet.
Terkait erat dengan memahami faktor-faktor yang memengaruhi sintasan hidup pasien diabetes meltius, penelitian ini bertujuan mengetahui peluang sintasan hidup pasien diabetes melitus, mengetahui faktor-faktor yang memengaruhi waktu sintasan terhadap sintasan hidup pasien diabetes melitus, dan menentukan model terbaik dalam menjelaskan hubungan antara variabel respon (waktu sintasan terhadap sintasan hidup pasien diabetes melitus) dengan variabel bebasnya yang berpengaruh nyata. Peneliti menggunakan data sekunder berupa data rekam medik pasien diabetes melitus periode 1 Januari 2016 sampai 31 Desember 2017 yang rawat inap di RSUD Wangaya Denpasar, lama waktu rawat inap sintasan pasien diabetes melitus dalam satuan hari (K) dengan variabel yang diduga memengaruhi berjumlah 8 variabel bebas, antara lain Usia (X1 ), jenis kelamin (X2 ), riwayat
keluarga/genetik (X3), status kadar gula darah (X4), penyakit yang menyertai (X5), rasa nyeri (X6), pemberian obat diabetes dan insulin (X7), dan indeks massa tubuh (X8).
Persamaan model untuk Cox proportional hazard adalah sebagai berikut:
h(t,X) = ⅛0∞exp(∑‰ ιβXi) (1)
dengan, h 0(t) menyatakan baseline hazard yang tidak perlu diketahui, Xi menyatakan variabel-variabel bebas terdiri dari X1 ,X2, ...,Xp, dan β i menyatakan parameter
dari variabel-variabel bebas terdiri dari Pl , P2,…,Pp .
Adapun langkah-langkah analisis data dalam penelitian ini adalah sebagai berikut:
-
1. Merekapitulasi data sekunder pasien diabetes melitus berdasarkan data tersensor interval.
-
2. Identifikasi karakteristik data pasien diabetes melitus.
-
3. Menduga fungsi sintasan, fungsi hazard, dan median waktu sintasan menggunakan metode Kaplan-Meier. Pendugaan tersebut bertujuan untuk mengetahui peluang sintasan hidup pasien diabetes melitus.
-
4. Menguji asumsi proportional hazard dengan menggunakan plot log minus log terhadap waktu sintasan (t) untuk setiap variabel bebas.
-
5. Melakukan uji signifikansi parameter secara parsial. Pengujian ini dilakukan untuk mengetahui pengaruh variabel bebas terhadap variabel respon.
-
6. Melakukan uji rasio likelihood dan
menyeleksi model dengan melihat perubahan nilai -2 log likelihood pada
model. Perubahan nilai tersebut diperoleh dengan membandingkan nilai -2 log likelihood antara model tanpa variabel bebas dan model dengan variabel bebas.
-
7. Menentukan model terbaik regresi Cox proportional hazard dengan metode backward elimination.
-
8. Interpretasi hasil.
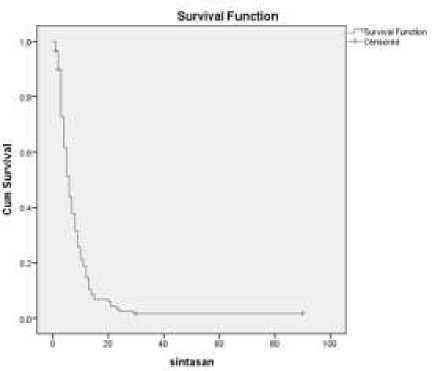
Gambar 1. Grafik Plot Fungsi Sintasan Pasien Diabetes Melitus
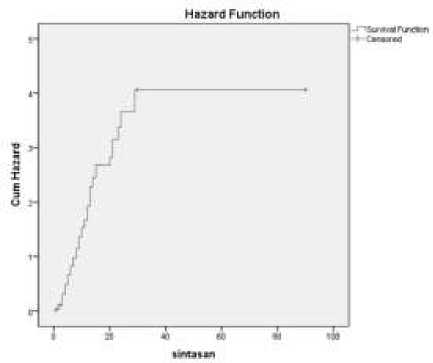
Gambar 2. Grafik Plot Fungsi Hazard Pasien Diabetes Melitus
Gambar 2 dapat dilihat bahwa grafiknya mengalami kenaikan setiap waktu, hal ini berarti bahwa pasien lebih berpeluang untuk mengalami kematian akibat diabetes melitus ini.
Pada persamaan (2), ̂(t) merupakan penduga fungsi sintasan, nj menyatakan individu yang berisiko mengalami kegagalan pada waktu t(j), untuk j=1,2,…,r, dandj merupakan individu yang mengalami kegagalan pada saat t(j).
ℎ̂(t)=A
(3)
Pada persamaan (3), h(t) merupakan penduga t(50) = min{tj∣5(ti) ≤ 0,5} (4)
fungsi hazard, t(j) ≤ t ≤ ta+i), untuk t(50) = 0,477 < 0,5
τi = t(j) - t(j-ιy = 5 hari (dilihat pada tabel 1)
Median waktu sintasan dapat dihitung
sebagai berikut:
Tabel 1. Fungsi Sintasan dan Fungsi Hazard Pasien Diabetes Melitus
|
Waktu Sintasan |
dj |
ni |
(n-dl ni |
sm |
h— |
|
1 |
4 |
119 |
0,966 |
0,966 |
0,034 |
|
2 |
8 |
111 |
0,928 |
0,896 |
0,072 |
|
3 |
0 |
91 |
0,780 |
0,699 |
0,220 |
|
4 |
13 |
78 |
0,833 |
0,583 |
0,167 |
|
5 |
2 |
66 |
0,818 |
0,477 |
0,182 |
|
6 |
9 |
57 |
0,842 |
0,402 |
0,158 |
|
7 |
7 |
50 |
0,860 |
0,345 |
0,140 |
|
8 |
7 |
43 |
0,837 |
0,289 |
0,163 |
|
9 |
7 |
36 |
0,806 |
0,233 |
0,194 |
|
10 |
5 |
31 |
0,839 |
0,195 |
0,161 |
|
11 |
3 |
28 |
0,893 |
0,174 |
0,107 |
|
12 |
5 |
23 |
0,783 |
0,136 |
0,217 |
|
13 |
5 |
18 |
0,722 |
0,099 |
0,278 |
|
14 |
2 |
16 |
0,875 |
0,086 |
0,125 |
|
15 |
2 |
14 |
0,857 |
0,074 |
0,143 |
|
20 |
1 |
13 |
0,923 |
0,068 |
0,015 |
|
21 |
2 |
11 |
0,818 |
0,056 |
0,182 |
|
23 |
1 |
10 |
0,900 |
0,050 |
0,050 |
|
24 |
1 |
9 |
0,889 |
0,045 |
0,111 |
|
29 |
1 |
8 |
0,875 |
0,039 |
0,025 |
Sumber: Data Diolah, 2018
Berdasarkan, Tabel 1 dapat diketahui bahwa probabilitas waktu sintasan pasien diabetes melitus selama 29 hari setelah menjalani perawatan pertama kali di RSUD Wangaya Denpasar adalah 0,039 atau 3,9%.
Pada persamaan (4), t(50) merupakan penduga median waktu sintasan. Hal ini menyatakan bahwa responden yang dirawat sebagai pasien diabetes melitus bisa hidup selama 5 hari sejak pertama kali menjalani
perawatan di RSUD Wangaya Denpasar dengan harapan hidup sebesar 50%.
-
2. Regresi Cox Proportional Hazard
-
a. Asumsi Pemodelan Cox Proportional
Hazard
Pengujian asumsi hazard proporsional terhadap waktu sintasan untuk masing-masing variabel bebas dapat diperiksa dengan metode grafik yaitu menggunakan plot. Berikut ini grafik plot log minus log dari kedelapan variabel bebas:
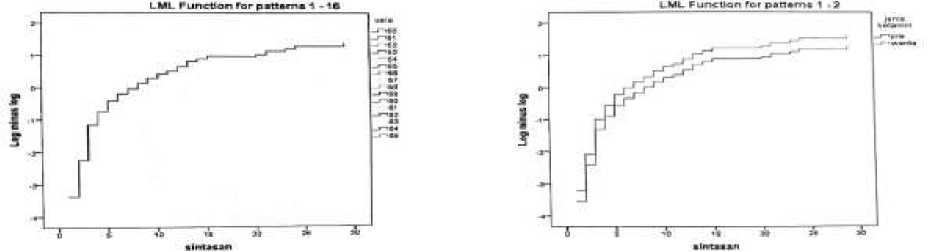
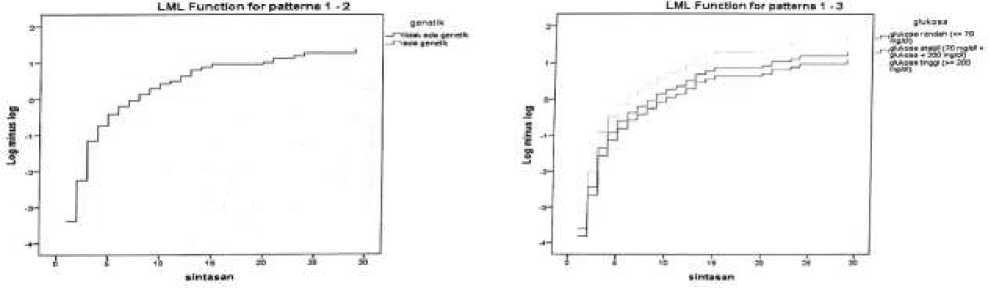
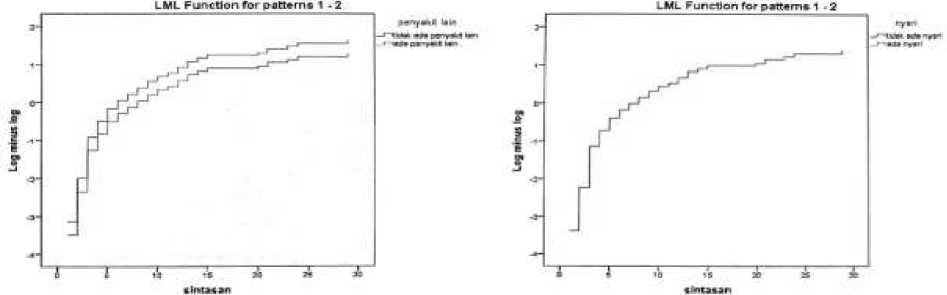
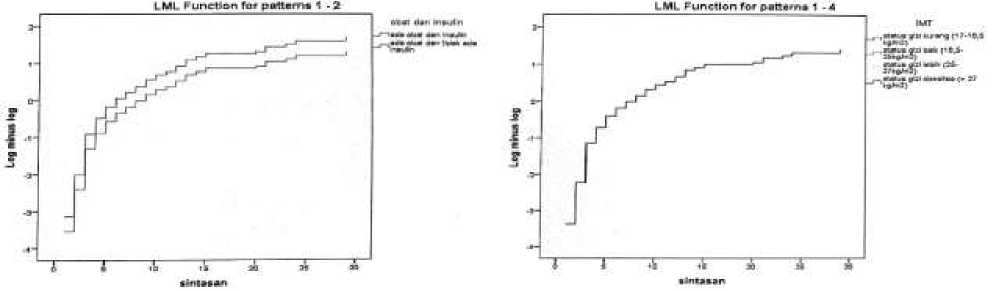
Gambar 3. Plot LML Waktu Sintasan Terhadap Kedelapan Variabel Bebas
b. Pengujian Signifikansi Parameter
Gambar 3 menunjukkan bahwa kedelapan variabel bebas membentuk garis yang sejajar satu sama lainnya, yang berarti kedelapan variabel bebas pasien diabetes melitus proporsional terhadap waktu dan dapat digunakan dalam model regresi Cox proportional hazard.
Pengujian secara parsial berfungsi untuk melihat ada tidaknya pengaruh nyata masing-masing variabel bebas yang ada terhadap waktu sintasan, dengan hipotesis sebagai berikut:
^o ∶ =0, denganj=1,2,…․,8
H1 ∶ ≠0, denganj=1,2,…․,8
Uji statistika yang digunakan adalah Uji Wald tolak H0, jika > , = 3,841.
dengan a = 0,05 dan daerah kritisnya adalah
Tabel 2. Hasil Uji Parsial Data Waktu Sintasan Pasien Diabetes Melitus
|
Variabel Bebas |
βi |
SE (βj ) |
Statis-tik Uji Wald |
P-value |
Keputusan |
|
Usia |
-0,001 |
0,017 |
0,005 |
0,942 |
Tidak cukup bukti menolak ¾ I |
|
Jenis kelamin |
0,506 |
0,208 |
5,902 |
0,015 |
Tolak H0 |
|
Genetik |
0,285 |
0,202 |
1,990 |
0,158 |
Tidak cukup bukti menolak Hq I |
|
Glukosa |
0,343 |
0,242 |
2,008 |
0,156 |
Tidak cukup bukti menolak ¾ I |
|
Penyakit lain |
-0,436 |
0,229 |
3,639 |
0,056 |
Tidak cukup bukti menolak Hq I |
|
Nyeri |
-0,060 |
0,223 |
0,072 |
0,789 |
Tidak cukup bukti menolak Hq I |
|
Obat & insulin |
-0,282 |
0,277 |
1,038 |
0,308 |
Tidak cukup bukti menolak Hq I |
|
IMT |
0,043 |
0,126 |
0,115 |
0,734 |
Tidak cukup bukti menolak Hq I |
|
Sumber: Data Diolah, 2018 c. Pengujian Rasio Likelihood Berdasarkan Tabel 2, menjelaskan bahwa Pengujian rasio likelihood bertujuan untuk secara parsial variabel bebas yang berpengaruh melihat pengaruh variabel-variabel bebas nyata terhadap waktu sintasan pasien diabetes secara simultan dan menentukan kepentingan melitus adalah jenis kelamin, sedangkan relatif dari masing-masing variabel bebas. variabel yang lain dianggap konstan. | |||||
Tabel 3. Hasil Analisis Pengujian Rasio Likelihood
|
Model Dengan Variabel Yang Disertakan |
-2 log likelihood |
Perubahan |
|
Tanpa variabel |
902,444 |
- |
|
Usia |
882,92 |
19,524 |
|
Jenis Kelamin |
889,365 |
13,079 |
|
Genetik |
901,876 |
0,568 |
|
Glukosa |
896,839 |
5,605 |
|
Penyakit Lain |
899,842 |
2,602 |
|
Nyeri |
902,281 |
0,163 |
|
Obat dan Insulin |
898,595 |
3,849 |
|
IMT |
902,126 |
0,318 |
|
Usia + Glukosa |
878,382 |
24,062 |
|
Usia + Obat dan Insulin |
879,627 |
22,817 |
|
Glukosa + Obat dan Insulin |
896,593 |
5.851 |
|
Usia + Glukosa + Obat dan Insulin |
877,873 |
24,571 |
Sumber: Data Diolah, 2018
Berdasarkan Tabel 3, dengan memodelkan variabel yang signifikan, diperoleh 4 model yang terdiri dari 2 sampai 3 variabel bebas. Dari keempat model yang ada, ditunjukkan bahwa model usia + glukosa + obat dan insulin memberikan nilai 24,571, sehingga perubahan -2 log likelihood yang digunakan dalam menentukan model terbaik adalah 24,571.
-
d. Pemodelan Cox Proportional Hazard
Pada Sintasan Pasien Diabetes Melitus
Penentuan model terbaik ini digunakan metode backward elimination.
Tabel 4. Hasil backward elimination Kedelapan Variabel Bebas
|
B |
Sig. |
Exp(B) | ||
|
Step 6 |
X2 |
0,443 |
0,024 |
1,557 |
|
X4 |
0,462 |
0,011 |
1,587 | |
|
X5 |
-0,447 |
0,037 |
0,640 | |
Sumber: Data Diolah, 2018
Berdasarkan Tabel 4, dapat disimpulkan bahwa model terbaik Cox proportional hazard
adalah sebagai berikut:
H(t,X)=ℎo(t)e0,443Xlg0, 462JC 2 q θ , 447X3
(5)
dengan, ℎQ(t) menyatakan baseline hazard dari model proporsional hazard regresi Cox,
^l menyatakan jenis kelamin, X2 menyatakan status kadar gula darah, dan X3 menyatakan penyakit yang menyertai.
Interpretasi Model
Berdasarkan Tabel 4, model Cox proportional hazard dapat diinterpretasikan sebagai berikut:
-
1. Jenis kelamin memiliki nilai sebesar 1,557, sebagai referensi menurut Irawan (2010) menyatakan bahwa wanita lebih rentan terkena diabetes melitus dibandingkan pria, yang berarti untuk setiap pasien diabetes melitus yang berjenis kelamin wanita memiliki waktu lebih cepat untuk mencapai kegagalan sebesar 1,557 kali dibandingkan pasien diabetes melitus yang berjenis kelamin pria.
-
2. Status kadar gula darah memiliki nilai sebesar 1,587, sebagai referensi menurut Sarifah (2001) membuktikan bahwa pengendalian kadar glukosa darah sampai mendekati normal atau stabil akan dapat mempertahankan hidupnya, yang berarti untuk setiap pasien diabetes melitus yang status kadar gula darahnya tinggi dan rendah memiliki waktu lebih cepat untuk mencapai kegagalan sebesar 1,587 kali dibandingkan pasien diabetes melitus yang memiliki status kadar gula darahnya normal atau stabil.
-
3. Penyakit yang menyertai memiliki nilai sebesar 0,640, sebagai referensi menurut Awad (2013) menyatakan bahwa sebagian besar seseorang yang mengidap diabetes melitus memiliki penyakit lain yaitu hipertensi (tekanan darah tinggi), yang berarti untuk setiap pasien diabetes melitus yang tidak ada penyakit lain selain diabetes melitus memiliki waktu lebih lambat untuk mencapai kegagalan sebesar 0,640 kali dibandingkan pasien diabetes melitus yang ada penyakit lain selain diabetes melitus.
-
4. KESIMPULAN DAN SARAN
Kesimpulan yang dapat diambil dari hasil dan pembahasan adalah sebagai berikut: 1. Penelitian ini menyimpulkan bahwa pada kurun waktu 1 sampai 29 hari terhitung sejak pasien diabetes melitus mulai dirawat di RSUD Wangaya Denpasar peluang pasien bertahan hidup kurang dari 5 hari sebesar 0,5 dan diakhir perawatan peluang bertahan hidup menurun menjadi 0,039.
-
2. Berdasarkan penelitian ini, dari kedelapan variabel bebas yang digunakan untuk memodelkan sintasan pasien diabetes melitus terdapat hanya tiga variabel bebas yang berpengaruh nyata secara statistika meliputi jenis kelamin sebesar 1,577, status kadar gula darah sebesar 1,587, dan penyakit yang menyertai sebesar 0,640.
Adapun saran yang bisa diberikan untuk penelitian selanjutnya adalah peneliti selanjutnya dapat mengembangkan lagi penelitian ini menggunakan metode statistika yang lain.
DAFTAR PUSTAKA
Anon. 2012. Jumlah Penderita Diabetes di Dunia. Tersedia dalam:
http://indodiabetes.com/data-statistik-jumlah-penderita-di-dunia-versi-who.html. Diakses 4 Oktober 2017.
Awad, N. 2013. Gambaran Faktor Resiko Pasien Diabetes Melitus Tipe II di Poliklinik Endokrin Bagian/SMF FK-UNSRAT RSU Prof. Dr. R. D. Kandou Manado Periode Mei 2011-Oktober 2011. Journal e-Biomedik, Volume 1, Nomor 1, halaman 45-49. Manado: Universitas Sam Ratulangi Manado.
Collett, D. 1994. Modelling Survival Data in Medical Reseacrh. London: Chapman and Hall.
Hasdianah. 2012. Mengenal Diabetes Melitus. In: Yogyakarta: Nuha Medika.
Irawan, D. 2010. Prevalensi dan Faktor Risiko Kejadian Diabetes Melitus Tipe 2 di Daerah Urban Indonesia. Thesis. Jakarta: Univeritas Indonesia.
Kleinbaum, D. & Klein, M. 2005. Survival Analysis: Statistics for Biology and
Health. Second Edition. New York: Springer-Verlag.
Lee, E. & Wang, J. W. 2003. Statistical Methods for Survival Data Analysis. Third Edition. New York: John Willey & Sons, Inc.
Rahayu, N., Setiawan, A. & Mahatma, T. 2012. Analisis Regresi Cox Proportional Hazards Pada Ketahanan Hidup Pasien Diabetes Melitus. Journal. Salatiga: Universitas Kristen Satya Wacana.
Sarifah. 2001. Faktor-faktor yang Memengaruhi Masih Tingginya Kadar Gula Darah Pada Pasien Diabetes Melitus yang Menjalani Terapi DM di Poli RSUP D.R. Sardjito Yogyakarta. Journal. Yogyakarta.
285
Discussion and feedback