PENENTUAN CADANGAN PREMI DENGAN PERHITUNGAN PROSPEKTIF UNTUK ASURANSI PENDIDIKAN

E-Jurnal Matematika Vol. 7 (2), Mei 2018, pp. 122-128

DOI: https://doi.org/10.24843/MTK.2018.v07.i02.p193

ISSN: 2303-1751

PENENTUAN CADANGAN PREMI DENGAN PERHITUNGAN PROSPEKTIF UNTUK ASURANSI PENDIDIKAN

Anggie Ezra Julianda Hutapea^1§, I Nyoman Widana², Luh Putu Ida Harini³

¹Program Studi Matematika, Fakultas MIPA – UniversitasUdayana [Email: anggie.hutapea02@gmail.com]

²Program Studi Matematika, Fakultas MIPA – UniversitasUdayana [Email:nwidana@yahoo.com]

³Program Studi Matematika, Fakultas MIPA – UniversitasUdayana [Email: ballidah@gmail.com]

^§Corresponding Author

ABSTRACT

The purpose of this research is to get formula to calculate premium reserve value with prospective calculation for education insurance. This study examines the value of premium reserves for people aged 40 years with a coverage period of 17 years. In determining the value of premium reserve using the prospective calculation. It will be started by completing the value of the Indonesian Mortality Table 2011 using the interest rate of 6.5%, calculating the cash value of the benefit, the annuity value, the net annual premium value, and the net monthly premium value. The results of this study indicate that the value of premium reserves with a prospective calculation for benefits paid at the end of the year and the premium reserve value for benefits paid at the time the insured dies, its value with the value of the cash price set by the insurer at the end of year- 17 on the insurance contract.

Keywords: Education insurance, the premium reserve, a prospective.

dalam mengatur cadangan premi. Akibatnya, perusahaan asuransi tidak mampu membayar uang pertanggungan kepada pihak tertanggung ketika jumlah klaim yang diajukan pihak tertanggung ternyata melebihi jumlah klaim yang diprediksi sebelumnya. Masalah tersebut dapat diantisipasi dengan menentukan cadangan premi dengan tepat (Destriani et al, 2014).

Metode perhitungan cadangan premi bersih ada dua yaitu perhitungan secara retrospektif dan perhitungan prospektif. Perhitungan secara retrosektif merupakan perhitungan cadangan premi berdasarkan jumlah total pendapatan diwaktu lampau. Sedangkan, perhitungan secara prospektif merupakan perhitungan cadangan premi berdasarkan nilai sekarang dari semua pendapatan diwaktu yang akan datang. Kedua metode ini menghasilkan hasil cadangan yang sama (Futami, 1993).

Penelitian ini bertujuan untuk mendapatkan formula cadangan premi untuk asuransi pendidikan dengan perhitungan prospektif dan menentukan besar cadangan premi untuk asuransi pendidikan dengan perhitungan

prospektif.

Selanjutnya dibahas komponen-komponen yang diperlukan dalam penentuan cadangan premi untuk asuransi pendidikan menggunakan metode perhitungan prospektif, yaitu:

Tingkat suku bunga adalah persentase pembayaran modal yang dipinjam dari lain pihak (Sukirno, 1994). Cara perhitungan tingkat suku bunga yang digunakan yaitu tingkat suku bunga majemuk (Futami, 1993):

1

V =-----

=₍₁₊i)

(1)

Nilai tunai manfaat adalah sejumlah uang pertanggungan diterima pihak tertanggung pada saat melakukan klaim. Nilai tunai dari manfaat untuk tiap satu unit pembayaran pada akhir tahun kematian [Futami, 1993]. Dirumuskan dengan persamaan:

₁ M_x -A¹ = ——

^zlY:=

^x+n + Dχ+∏

D_x

yang pembayaran

(2)

preminya

Suatu anuitas dikaitkan pada anuitas hidup

kematian seseorang disebut

(Futami, 1993). Untuk

menghitung Actuarial Present Value (nilai sekarang) dari anuitas hidup didefinisikan (Dickson, 2009):

n-1

̈X:̅̅̅|=∑V^k ․ kPx

k=0

N-

D_x

(3)

Suatu anuitas awal dalam satu tahun dilakukan sebanyak k kali pembayaran dan besarnya tiap kali pembayaran adalah dengan pembayaran n tahun disebut anuitas hidup berjangka (Sembiring, 1986). Dirumuskan sebagai berikut:

₍ k ₎

̈ _̅⁾_̅̅| =̈_:̅̅̅_| -       (1-vⁿ_np_x)(4)

:|      ^:|

Premi adalah sejumlah uang yang harus dibayarkan sebagai suatu kewajiban dari pihak tertanggung. Untuk menghitung premi tahunan digunakan persamaan (Dickson, 2009):

P= - ^:̅̅̅| (5) a■X:^̅̅̅|

Premi bulanan adalah premi yang dibayarkan 12 kali dalam satu tahun (Futami, 1993). Premi bulanan dapat ditentukan dengan menggunakan prinsip ekuivalensi:

12. P⁽ 12⁾. ̈⁽.^{1 ̅̅̅}| = A                                   (6)

:|       ^:|

Menurut (Dickson, 2009), cadangan adalah ekspektasi nilai sekarang dari variabel acak kerugian bersih yang akan terjadi dimasa yang akan datang. Persamaannya sebagai berikut:

1

tK=(v. dχ + t + V². dχ+t+ι+⋯

<∙x+t

+ _vn t . dχ+n-l)-p(lχ+t +V. lχ+t+ι+⋯

+ _vn t 1 . ^x+n-l)                        (7)

• 2.    METODE PENELITIAN

Penelitian ini menggunakan data sekunder, yaitu data yang diperoleh dari salah satu perusahaan asuransi. Pengolahan data pada penelitian ini dibantu dengan menggunakan Software Microsoft Exel. Langkah-langkah yang dilakukan pada penelitian ini adalah sebagai berikut:

• a.    Melengkapi nilai tabel mortalitas berdasarkan Tabel Mortalitas Indonesia 2011.

• b.    Membuat tabel komutasi yang berisi nilai v dan fungsi-fungsi komutasi.

• c.    Menentukan formula untuk penentuan cadangan premi asuransi pendidikan.

• d.    Melakukan perhitungan premi asuransi pendidikan untuk pihak tertanggung yang berusia x tahun dengan benefit yang dibayarkan pada akhir tahun dengan langkah-langkah: (a) menghitung nilai tunai manfaat; (b) menghitung nilai anuitas hidup berjangka; (c) menghitung anuitas hidup berjangka dengan pembayaran dilakukan 12 kali dalam setahun; (d) menghitung premi tahunan bersih; (e) menghitung premi bulanan bersih; (f) menentukan formula untuk penentuan besar cadangan premi.

• e.    Menentukan besar cadangan premi asuransi pendidikan untuk benefit yang dibayarkan pada akhir tahun dengan perhitungan prospektif.

• f.    Melakukan perhitungan premi asuransi pendidikan untuk pihak tertanggung yang berusia x tahun dengan benefit yang dibayarkan pada pihak tertanggung meninggal dunia dengan langkah-langkah: (a) menghitung nilai tunai manfaat; (b) menghitung nilai anuitas hidup berjangka; (c) menghitung anuitas hidup berjangka dengan pembayaran  12 kali dalam setahun; (d)

menghitung  premi  tahunan  bersih;  (e)

menghitung  premi  bulanan  bersih;  (f)

menentukan formula untuk penentuan cadangan premi.

• g.    Menentukan besar cadangan premi asuransi pendidikan untuk benefit yang dibayarkan pada saat pihak tertanggung meninggal dunia dengan perhitungan prospektif.

3I. HASIL DAN PEMBAHASAN

Dalam melengkapi nilai tabel mortalitas diawali dengan menghitung nilai d_x menggunakan persamaan yang dapat ditulis sebagai berikut:

d_x =  ^- lχ+l                           (8)

Langkah selanjutnya adalah membuat tabel komutasi. Pada pembuatan tabel komutasi dilakukan perhitungan nilai v dan nilai fungsi-fungsi komutasi yaitu D_x , N_x , ^x , M_x , ^̅dan ^̅ X dengan menggunakan suku bunga konstan yaitu

i = 6,5% . Perhitungannya adalah:
1. Perhitungan nilai v adalah: 1 v= 1+i	(9)
2. Perhitungan nilai ^X adalah: ^x =   .	(10)
3. Perhitungan nilai Nx adalah: Nx =  + Dx+ι + Dx+2+⋯+Bω-ι	(11)
4. Perhitungan nilai ^X adalah: ^x =	(12)
5. Perhitungan nilai Mx adalah: Mx =  + ^X+1 + ^X + 2+⋯+ ^ω-l	(13)
6. Perhitungan nilai ̅ adalah: ̅ =      . dx	(14)
7. Perhitungan nilai ̅x adalah: ̅x= ̅X+ ̅t+1 + ̅t+2+⋯+ ̅υ-l	(15)
Selanjutnya,  menentukan  formula	dengan

perhitungan prospektif untuk menentukan besar nilai cadangan premi. Adapun rincian kontrak

dalam program asuransi yang digunakan dalam penelitian ini adalah sebagai berikut: pihak tertanggung berusia x tahun dengan jangka waktu pertanggungan selama n tahun. Pihak tertanggung akan menerima sejumlah uang pertanggungan sebesar Rp.5.000.000 pada saat pihak tertanggung meninggal sebelum akhir kontrak dan tetap hidup pada akhir kontrak. Pihak tertanggung juga mendapatkan dana kelangsungan belajar sebesar Rp.500.000 pada tanggal 1 Juli 2008, Rp.1.000.000 pada tanggal 1 Juli 2014, Rp.1.500.000 pada tanggal 1 Juli 2017 dan Rp.2.000.000 yang akan dibayarkan sekaligus pada akhir kontrak yaitu 1 Juli 2020. Dana kelangsungan belajar dinotasikan dengan ^Apt . Berdasarkan kontrak tersebut, maka pada persamaan (7) dimodifikasi sehingga diperoleh formula untuk penentuan besar nilai cadangan premi dengan benefit yang dibayarkan pada akhir tahun yaitu:

1

tVx ⁼     [5.10⁶(V^. dχ + t + v²d_x+t+1+⋯

+V^{n t}. dχ+n-l + V^{n t} . lχ+n)]-p(lχ+t

+V^. lχ+t+ι+⋯+_vn t 1 ^. lχ+n-l)

+AP_t                             (16)

Kemudian dipermudah kedalam bentuk fungsi komutasi yaitu:

Kemungkinan peluang orang meninggal yang dinotasikan dengan:

(V. dχ+t + V² . d_x+_t+ι+⋯+v^{n t} . dχ+n-l )

Dimisalkan dengan A , sehingga diperoleh:

V.d

=

V.d

+ V². ⅛ + t+l+⋯+V^{n t} . d.

l_X+t

+ V² . ⅛+t+ι +⋯+V∏+X-X-t . d.

lχ + t

_ /V. d_x+t + V² . d_x+t+ι+⋯+ ^n+x-x-t .d

∖                       lχ+t

∖ V^x+t ).

x+n-l^

. d_x+t

+ pX÷t+2 . dχ+t+l+⋯+ .yX+n . d.

D:

+ ^X+t+l +⋯+Cχ+n

M_x+t

D

_-

D_x+t

Mχ+∏

x+t

⁽lχ+t +V. lχ+t+l+⋯+V'

. lχ+n-l⁾

_d   lχ + t +V. lχ + t+l+⋯+       . lχ+n-l

^B=

_ lχ+t +Z. lχ+t+ι+⋯+ ^n-t-l . lχ+t-t+n-l lχ+t

₌ ∕lχ+t +v. lχ+t+ι+⋯+ ^n-t-l . lχ+t-t+n-l∖ V^x+t

=(                lχ+t                )._vx₊t

⁽Dχ+t)+(⅞+t+ι)+(⅞+t + 2)+⋯+(Dχ+t+n-t-l⁾ Dχ+t

_ N_x+t ^- Nχ+n Pχ+t

Sehingga diperoleh formula cadangan premi yang benefitnya dibayarkan pada akhir tahun dalam bentuk fungsi komutasi yaitu:

Dari persamaan (4) akan dihitung nilai anuitas hidup berjangka (pembayaran 12 kali dalam setahun) untuk benefit yang dibayarkan pada akhir tahun dan pada saat pihak tertanggung meninggal dunia, diperoleh:

̈⁽ ________ ^w40 :^̅̅̅̅̅|

12-1

^{40:1̅̅7̅̅|-}2(12)     ^-V 17 P40)

=10,56044-(¹¹)(1-(0,3428)(0,9196))

= 10,24659712

Sebelum menghitung premi tahunan bersih dengan benefit yang dibayarkan pada akhir tahun, terlebih dahulu dilakukan perhitungan nilai tunai manfaat dana kelangsungan belajar untuk pihak tertanggung yang berusia 40 tahun dan jangka waktu 17 tahun. Uang pertanggungan yang didapat sebesar Rp.5.000.000 dan pihak tertanggung juga akan mendapat dana kelangsungan belajar sebesar Rp.500.000 pada tanggal 1 Juli 2008, Rp.1.000.000 pada tanggal 1 Juli 2014, Rp.1.500.000 pada tanggal 1 Juli 2017 dan Rp.2.000.000 pada tanggal 1 Juli 2020 yang dibayarkan sekaligus dengan uang pertanggungan, sehingga diperoleh:

P          β ∕ ^40 - M₅₇ + ^57          6 ς

A^p₄₀: =5.10 (          ⁺   )_{+5×10 .} V⁵

+1×10⁶. V¹¹+1,5×10⁵. V¹⁴

+2×10⁶. V¹⁷

= 3.949.258,44

Selanjutnya, dilakukan perhitungan untuk premi tahunan bersih asuransi pendidikan dengan benefit yang dibayarkan pada akhir tahun menggunakan persamaan (5):

=     :

̈ 40:^̅̅̅̅̅|

3.949.258,44

⁼ 10,56044043

= 373.967,21

Menggunakan persamaan (6), nilai premi bulanan bersih asuransi pendidikan untuk benefit yang dibayarkan pada akhir tahun untuk pihak tertanggung yang berusia 40 tahun dengan jangka waktu pertanggungan selama 17 tahun adalah:

p⁽12⁾. ̈⁽ 12)₌τ

40:̅̅̅̅̅| =       :

p (12       3.949.258,44

⁼ (12)(10,24659712)

= 32.118,45

Sebelum menentukan besar nilai cadangan premi, terlebih dahulu dihitung dana kelangsungan belajar untuk mendapatkan baris pertama AP₁ , didapatkan dengan menggunakan persamaan:

AP₁=5.10⁵× v⁴+1.10⁶× V¹⁰

+1,5.10⁶× V¹³ +2.10⁶× V¹⁶

AP₁=5.10⁵×0,77+1.10⁶ × 0,53

+1,5.10⁶×0,44+2.10⁶ × 0,36

= 2.313.103,38

Berlaku juga untuk seterusnya. Hasil selengkapnya dapat dilihat pada tabel 1.

Tabel 1. Nilai Dana Kelangsungan Belajar

Akhir Tahun Ke- (t)	APt
1	2.313.103,38
2	2.463.455,10
3	2.623.579,68
4	2.794.112,36
5	2.975.729,66
6	2.636.652,09
7	2.808.034,48
8	2.990.556,72
9	3.184.942,91
10	3.391.964,20
11	3.612.441,87
12	2.782.250,59
13	2.963.096,88
14	3.155.698,18
15	1.763.318,56
16	1.877.934,27
17	2.000.000

Setelah diperoleh nilai dana kelangsungan belajar (APt) maka akan ditentukan besar nilai cadangan premi untuk benefit yang dibayarkan pada akhir tahun dengan menggunakan persamaan (17):

Cadangan Premi Tahun Ke-1:

• *5.10:⁽ ⅞1 )+  ^. ^ +-i^{(     )}

V40 ⁼                                  + Ar γ

berlaku juga untuk seterusnya. Hasil

selengkapnya dapat dilihat pada tabel 2.

Tabel 2. Cadangan Premi untuk Benefit yang Dibayarkan pada Akhir Tahun

Jangka waktu pertanggungan (n)	Nilai Cadangan Premi untuk Benefit yang Dibayarkan pada Akhir Tahun
1	Rp. 387.679,17
2	Rp. 799.491,46
3	Rp. 1.237.216,22
4	Rp. 1.702.569,87
5	Rp. 2.197.297,05
6	Rp. 2.190.702,24
7	Rp. 2.715.177,68
8	Rp. 3.272.813,90
9	Rp. 3.865.941,21
10	Rp. 4.497.157,93
11	Rp. 5.169.223,76
12	Rp. 4.820.282,28
13	Rp. 5.551.476,85
14	Rp. 6.256.607,58
15	Rp. 5.452.632,97
16	Rp. 6.198.802,74
17	Rp. 7.000.000,00

Perbandingan Harga Tunai dengan Cadangan Premi

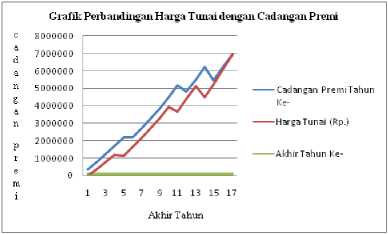
Gambar 1. Perbandingan Harga Tunai dengan Cadangan Premi

Selanjutnya, berdasarkan persamaan (2) dihitung nilai tunai manfaat yang dibayarkan pada saat pihak tertanggung meninggal dunia yang dinotasikan dengan ∕ ^̅X _:̅̅̅|  dikalikan dengan

1

(1+i)2 dapat ditulis sebagai berikut:

((M_x ^- Mχ+n)(1+i)²+ Dχ+n)

D

((«40 - «40 + 17)(1 + 0,065)²+ ¾0+17

^̅P

:^̅̅̅̅̅|

((1.072,06 - 758,36)(1 + 0,065)2 + 2.459,11)

7.800,49

= 0,356752493

Sebelum menghitung nilai premi tahunan, terlebih dahulu dihitung nilai tunai manfaat dana kelangsungan belajar dengan benefit yang dibayarkan pada saat meninggal, diperoleh:

((«4» - ^40+17)(1 + 0,065)² + ¾0+17)

^̅40 ̅̅̅̅̅ = 5.000.000

+500.000. V≡ + 1.000.000. V¹¹ + 1.500.000. V¹⁴

+2.000.000. V¹⁷

= 3.955.690,52

Selanjutnya, dilakukan perhitungan untuk premi tahunan bersih asuransi pendidikan berdasarkan persamaan (5) dan nilai anuitas hidup yang sudah diperoleh sebelumnya, sehingga:

A

40:̅1̅7̅̅|

40:̅1̅7̅̅|

3.955.690,52

10,56044043

= 374.576,28

Berdasarkan persamaan (6) dan nilai tunai manfaat dana kelangsungan belajar, dihitung nilai premi bulanan asuransi pendidikan dengan benefit yang dibayarkan pada saat pihak tertanggung meninggal dunia:

p(12⁾. ̈⁽ 12 ̅⁾̅̅̅̅ = ^{̅ i .}       :^̅̅̅̅̅| =

p(12)₌

i^p

40:^̅1^̅7^̅̅|

3.955.690,52

(12)(10,24659712)

= 32.170,76

Berdasarkan persamaan (18) dan nilai dana kelangsungan belajar AP_t yang sudah diperoleh sebelumnya, maka dapat ditentukan besar nilai cadangan premi dengan benefit yang dibayarkan pada saat pihak tertanggung meninggal dunia: Cadangan Premi Tahun Ke-1:

1      ,      I /W₄₁ + ⅛7∖ .

1̅40 ⁼    [5. 10 (1+i)²(    ⁺    )+5.10

Lχ+t                ×   ¼1   ×

^× I₅₇ . v¹⁶ -p( ⁿ-^)]+AP₁

Tabel 3. Cadangan Premi untuk Benefit yang Dibayarkan pada Saat Meninggal Dunia

Jangka waktu pertanggungan (n)	Nilai Cadangan Premi untuk Benefit yang Dibayarkan pada Saat Meninggal Dunia
1	Rp. 388.083,75
2	Rp. 800.292,50
3	Rp. 1.238.406,83
4	Rp. 1.704.139,70
5	Rp. 2.199.228,87
6	Rp. 2.192.968,38
7	Rp. 2.717.739,31
8	Rp. 3.275.620,30
9	Rp. 3.868.928,90
10	Rp. 4.500.249,72
11	Rp. 5.172.321,36
12	Rp. 4.823.264,58
13	Rp. 5.517.487,72
14	Rp. 6.258.923,51
15	Rp. 5.454.368,54
16	Rp. 6.199.772,06
17	Rp. 7.000.000,00

Penentuan cadangan premi untuk asuransi pendidikan dengan perhitungan prospektif menggunakan orientasi waktu yang akan datang. Nilai cadangan dilihat berdasarkan usia awal pihak tertanggung saat memulai asuransi dan memperhatikan manfaat-manfaat yang harus dibayarkan oleh perusahaan kepada pihak tertanggung, dalam kasus ini adalah dana kelangsungan belajar. Dana kelangsungan belajar yang dikembalikan oleh pihak perusahaan asuransi sebesar Rp.500.000 pada tahun ke-5, Rp.1.000.000 pada tahun ke-11, Rp.1.500.000 pada tahun ke-14 dan Rp.2.000.000 pada tahun ke-17 yang sekaligus dibayarkan dengan uang pertanggungan sebesar Rp.5.000.000.

• 4. SIMPULAN DAN SARAN

• A. Simpuan Penelitian

Penelitian ini menunjukkan bahwa formula menggunakan perhitungan prospektif untuk menentukan besar nilai cadangan premi dengan benefit yang dibayarkan pada akhir tahun dirumuskan dengan:

• ¹        M_x+t - Mχ+n∖ ,

tVx ⁼     [5. 10 ( W ---z+n)+^■x+n . Vⁿ t]

Lχ+t        × ^x+t ×

berlaku juga untuk seterusnya. Hasil selengkapnya dapat dilihat pada tabel 3.

-P(

_-

D.

Nχ+n)+AP_t -t.         '

dan formula menggunakan perhitungan prospektif untuk menentukan besar nilai cadangan premi dengan benefit yang dibayarkan pada saat pihak tertanggung meninggal dunia dirumuskan dengan:

_̅= ¹      ₆ n   . i(Mχ+t ⁺ Mχ+_n\

t ⁼     [5.10 _{(1+ )} (            )

⅛+t                ' ^υx+t '

+5. 10⁶×l ^. Vⁿ t

• _r. (Nχ+t + Nχ+n∖ , . _r.

• -P( X+1   )+AP_t

Untuk hasil analisis penentuan cadangan premi menggunakan perhitungan prospektif untuk benefit yang dibayarkan pada akhir tahun ataupun nilai cadangan premi untuk benefit yang dibayarkan pada saat pihak tertanggung meninggal dunia sama dengan nilai harga tunai yang ditetapkan oleh pihak perusahaan pada akhir tahun ke-17.

B. Saran

Pada penelitian ini penulis menentukan besar nilai cadangan premi untuk asuransi pendidikan dengan asumsi bunga konstan, disarankan untuk penelitian selanjutnya menggunakan jenis asuransi jiwa yang lain dan menggunakan tingkat suku bunga yang tidak konstan.

DAFTAR PUSTAKA

Destriani, Satyahadewi, N. & Mara, M.N., 2014. Penentuan Prospektif pada Asuransi Jiwa Seumur Hidup Menggunakan Metode New Jersey. Buletin Ilmiah Mat.Stat dan Terapannya (BIMASTER), No.3, Pp.7-12.

Dickson, D.C.M., Hardy, M.R & Waters, H.R., 2009. Actuarial Mathematics for Life Contingent Risk. New York: Cambridge UniversityPress.

http://bookzz.org./md5/C4ADC30B53F17D6 B9B989D728A56DB11. Diakses 02 Februari 2017.

Futami, T. 1993. Matematika Asuransi Jiwa Bagian I. Herliyanto G, penerjemah. Tokyo: Oriental Life Insurance Cultural Development Center. Terjemahan dari: Seime Hoken Sugaku Gekan ("92 Revision).

Prodjodikoro, W. 1987. Hukum Asuransi di Indonesia, Jakarta: Intermasa.

Sembiring, R. 1986. Buku Materi Pokok Asuransi I Modul 1-5. Jakarta: Karunika.

Sukirno, S. 1994. Pengantar Teori Makro. Jakarta: Raja grafindo.

128