PERAMALAN PERSEDIAAN INFUS MENGGUNAKAN METODE AUTOREGRESSIVE INTEGRATED MOVING AVERAGE (ARIMA) PADA RUMAH SAKIT UMUM PUSAT SANGLAH
on
E-Jurnal Matematika Vol. 7 (2), Mei 2018, pp. 129-133
DOI: https://doi.org/10.24843/MTK.2018.v07.i02.p194
ISSN: 2303-1751
PERAMALAN PERSEDIAAN INFUS MENGGUNAKAN METODE AUTOREGRESSIVE INTEGRATED MOVING AVERAGE (ARIMA) PADA RUMAH SAKIT UMUM PUSAT SANGLAH
I Putu Yudi Prabhadika1, Ni Ketut Tari Tastrawati2, Luh Putu Ida Harini 3
1Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: yudiprabhadika@yahoo.com]
2Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: taritastrawati@yahoo.com]
3Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: ballidah@gmail.com]
ABSTRACT
Infusion supplies are an important thing that must be considered by the hospital in meeting the needs of patients. This study aims to predict the need for infusion of 0.9% 500 ml of NaCl and 5% 500 ml glucose infusion at Sanglah General Hospital (RSUP) Sanglah so that the hospital can estimate the many infusions needed for the next six months. The forecasting method used in this research is the autoregressive integrated moving average (ARIMA) time series method. The results of this study indicate the need for infusion at Sanglah Hospital as many as 154,831 units for infusion of 0.9% NaCl 500 ml and 8,249 units for 5% 500 ml Glucose infusion.
Keywords: infusion supply, forecasting, Autoregressive Integrated Moving Average (ARIMA)
Persediaan infus merupakan salah satu hal penting yang perlu diperhatikan pihak rumah sakit selaku penyedia layanan kesehatan untuk memenuhi kebutuhan pasien. Dalam menentukan jumlah kebutuhan infus untuk periode berikutnya, pihak rumah sakit dapat melakukan peramalan dengan menggunakan metode analisis deret waktu. Data deret waktu atau data berkala adalah sekumpulan data hasil dari pengamatan historis yang menggambarkan secara kronologis suatu karakteristik populasi dimana kaitan variabel waktu dengan pengamatan diperhatikan, sehingga data dianggap sebagai fungsi atas waktu (Gujarati, 2004). Urutan-urutan nilai variabel yang diamati pada interval waktu yang sama diberi spasi disebut sebagai deret waktu (Makridakis, et al., 1997). Peramalan merupakan ilmu dalam memprediksi kejadian masa depan, yang melibatkan pengambilan data historis dan memproyeksikannya ke masa depan dengan menggunakan model matematis (Heizer, et al., 2014).
Salah satu metode peramalan dalam analisis deret waktu adalah metode autoregressive integrated moving average (ARIMA). Metode ARIMA adalah metode peramalan yang dikembangkan oleh George Box dan Gwilym Jenkins sehingga nama mereka kerap kali disinonimkan dengan proses ARIMA yang diterapkan untuk analisis data dan peramalan data runtun waktu. Terdapat 3 syarat agar metode ARIMA dapat digunakan dalam peramalan, yaitu data bersifat stasioner, residual model menyebar normal dan bersifat white noise. Menurut Wei (2006) model ARIMA dengan orde (p,d,q) dituliskan dengan persamaan sebagai berikut:
φp mi-B )dZt = θq(B>t Penelitian mengenai metode ARIMA telah dilakukan oleh Machmudin dan Ulama (2012) mengenai Peramalan Temperatur Udara di Kota Surabaya dengan Menggunakan ARIMA dan Artificial Neural Network. Namun, model ARIMA dari hasil penelitian tersebut masih belum baik sehingga penelitian selanjutnya
dapat memperbaiki model. Adapun untuk ANN Backpropagation memberikan model yang cukup baik dan dapat dikembangkan pada model ANN lainya.
Berdasarkan penelitian tersebut, peneliti tertarik untuk menerapkan model ARIMA dalam melakukan peramalan kebutuhan infus di RSUP Sanglah untuk periode Juli – Desember 2017. Adapun infus yang dianalisis adalah infus jenis NaCl 0,9% 500 ml dan infus jenis glukosa 5% 500 ml. Penelitian ini bertujuan untuk meramalkan kebutuhan kedua infus tersebut untuk memudahkan pihak RSUP Sanglah dalam menentukan persediaan infus untuk enam bulan berikutnya.
-
2. METODE PENELITIAN
Jenis dan Sumber Data
Jenis data yang digunakan dalam penelitian ini adalah data kuantitatif yaitu data history total pemakaian infus NaCl 0,9% 500 ml dan infus glukosa 5% 500 ml di RSUP Sanglah setiap bulannya selama 30 bulan (Januari 2015 - Juni 2017).
Metode Analisis Data
Langkah analisis dalam penelitian ini adalah sebagai berikut :
-
1. Identifikasi plot deret waktu
Melakukan identifikasi plot deret waktu penting dilakukan untuk mengetahui pengaruh trend an musiman dalam data. Jika masih terdapat pengaruh trend dan musiman, akan dilakukan differencing pada data.
-
2. Uji Stasioneritas
Uji stasioneritas perlu dilakukan untuk membuktikan bahwa data telah bersifat stasioner. Salah satu uji yang sering dipergunakan adalah uji Augmented Dickey-Fuller (ADF) dengan hipotesis:
Hq : Data tidak stasioner
H^ : Data stasioner
-
3. Menentukan model ARIMA
Dalam menentukan model ARIMA dari masing-masing variabel, dapat dilihat dari
plot autokorelasi (ACF) dan plot autokorelasi parsial (PACF) yang telah stasioner.
-
4. Menghitung Estimasi Parameter Model Pendugaan parameter dilakukan untuk menduga nilai dari parameter-parameter yang berpengaruh dalam model. Metode yang digunakan dalam pendugaan parameter adalah metode maximum likelihood estimation. Adapun hipotesisnya:
ττo o j ∙ ∙ γ∙λ
Hq: =0, parameter signifikan
ττ , , ∙ιι ∙
Hy: ≠0, parameter tidak signifikan
-
5. Uji Diagnostik Model
Uji diagnostik dilakukan untuk mengetahui apakah model-model ARIMA telah memenuhi sifat white noise. Untuk mengetahui model telah memenuhi sifat white noise dapat dilakukan dengan uji Ljung-Box dengan hipotesis sebagai berikut:
Hq : = =⋯= =0; tidak terdapat
autokorelasi antar residual model
Hy : minimal ada satu Pi≠0, dengan i=1,2,…,k ; terdapat autokorelasi antar residual model.
-
6. Uji Kenormalan Galat
Setelah model memenuhi sifat white noise, selanjutnya dilakukan uji Shapiro-Wilk untuk mengetahui kenormalan residual data dengan hipotesis sebagai berikut :
Hq : Residual menyebar normal,
: Residual tidak menyebar normal
-
7. Pemilihan Model Terbaik
Jika model telah memenuhi semua uji, maka akan dipilih model terbaik berdasarkan nilai Akaike Information Criterion (AIC) terkecil. Selanjutnya dilakukan peramalan kebutuhan infus NaCl 0,9% 500 ml dan infus glukosa 5% 500 ml dengan model yang terpilih.
-
8. Menghitung Keakuratan Model Peramalan Mengukur seuatu keakuratan model peramalan diperlukan untuk menunjukkan seberapa jauh data yang diketahui bisa menghasilkan model peramalan yang baik. Indikator yang umumnya digunakan dalam mengukur keakuratan model adalah Mean
Absolute Percentage Error (MAPE) yang dapat dicari dengan rumus:
∑ | |.100%
=
m
Keterangan:
-
= data asli pada saat t
-
= data hasil peramalan pada saat t
-
= banyak data
Adapun kriteria peramalan MAPE yaitu:
-
< 10% : Peramalan sangat akurat
10% - 20% : Peramalan baik
20% - 50% : Peramalan masuk akal (wajar)
-
> 50% : Peramalan tidak akurat
(Zhang, et al., 2015)
-
3. HASIL DAN PEMBAHASAN
Identifikasi Plot dan Uji Stasioneritas
Data yang dipergunakan dalam penelitian ini adalah data pemakaian infus NaCl 0,9% 500 ml dan infus glukosa 5% 500 ml selama periode Januari 2015 sampai dengan Juni 2017. Adapun plot dekomposisi dari kedua data dapat dilihat pada Gambar 1 dan Gambar 2.
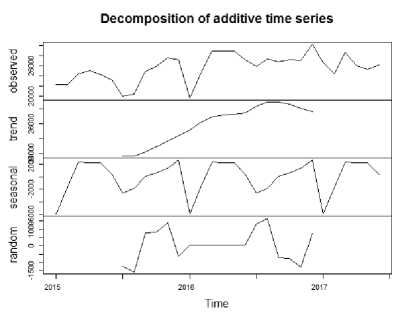
Gambar 1. Plot Dekomposisi NaCl
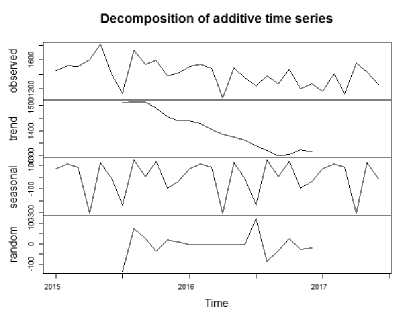
Gambar 2. Plot Dekomposisi Glukosa
Identifikasi plot menunjukkan ada pengaruh trend dan musiman pada data infus NaCl dan infus glukosa, oleh sebab itu dilakukan differencing sebanyak satu kali terhadap trend. Selanjutnya dilakukan uji stasioneritas dengan menggunakan Augmented Dickey-Fuller dengan hipotesis:
: Data tidak stasioner
: Data stasioner
Hasil uji stasioneritas dapat dilihat pada Tabel 1.
Tabel 1. Hasil Uji ADF
|
Data |
ADF |
Lag Order |
p-value |
|
NaCl |
5,7378 |
3 |
0,01 |
|
Glukosa |
-6,1793 |
3 |
0,01 |
Nilai p-value pada Tabel 1 untuk kedua data signifikan terhadap = 0,05. Hal tersebut menunjukkan kedua data telah stasioner.
Penentuan Model ARIMA
Penentuan model untuk kedua variabel dapat dilihat dari plot ACF dan PACF data yang telah stasioner. Plot tersebut dapat dilihat pada Gambar 3 dan Gambar 4.
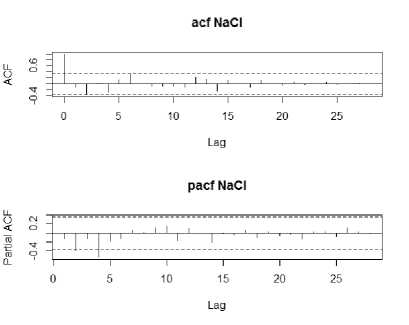
Gambar 3. Plot ACF dan PACF Infus NaCl
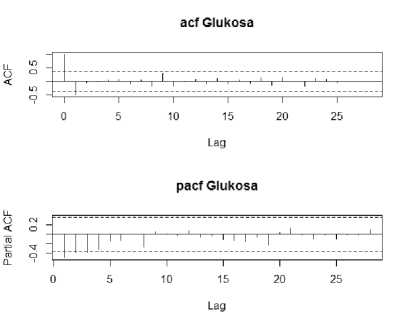
Gambar 4. Plot ACF dan PACF Infus Glukosa
Hasil dari identifikasi plot ACF dan PACF dari kedua data yaitu model yang akan diuji untuk data infus NaCl adalah model ARIMA (0,1,2), ARIMA (2,1,0), ARIMA (4,1,0), ARIMA (2,1,2), dan ARIMA (4,1,2). Sedangkan untuk data infus glukosa model yang akan diuji adalah ARIMA (0,1,1), ARIMA (1,1,0), ARIMA (2,1,0), ARIMA (1,1,1), dan ARIMA (2,1,1).
Pemilihan Model Terbaik
Setelah model ARIMA yang telah terbentuk melewati estimasi parameter, uji diagnostik, dan uji kenormalan galat, selanjutnya akan ditentukan model terbaik dari masing masing data berdasarkan nilai AIC. Adapun nilai AIC dari masing-masing model dapat dilihat pada Tabel 2 dan Tabel 3.
Tabel 2. Nilai AIC Data Infus NaCl
|
No |
Model |
Nilai AIC |
|
1 |
ARIMA (4,1,0) |
533,1815 (terkecil) |
|
2 |
ARIMA (2,1,2) |
538,5459 |
|
3 |
ARIMA (4,1,2) |
536,6799 |
|
4 |
ARIMA (0,1,2) |
535,3512 |
Data diolah : Tahun 2017
Tabel 3. Nilai AIC Data Infus Glukosa
|
No |
Model |
Nilai AIC |
|
1 |
ARIMA (1,1,0) |
395,8059 |
|
2 |
ARIMA (0,1,1) |
386,1634 |
|
3 |
ARIMA (2,1,0) |
392,6801 |
|
4 |
ARIMA (2,1,1) |
388,2981 |
|
5 |
ARIMA (0,1,2) |
386,7882 |
|
6 |
ARIMA (4,1,0) |
388,1015 |
|
7 |
ARIMA (2,1,2) |
385,2280 (terkecil) |
|
8 |
ARIMA (4,1,2) |
391,6480 |
Data diolah : Tahun 2017
Berdasarkan Tabel 2 dan Tabel 3, diketahui bahwa model terbaik untuk meramalkan kebutuhan infus NaCl 0,9% 500 ml adalah model ARIMA (4,1,0) sedangkan model terbaik yang digunakan untuk meramalkan kebutuhan infus glukosa 5% 500 ml adalah ARIMA (2,1,2).
Peramalan Kebutuhan Infus NaCl dan Glukosa di RSUP Sanglah
Setelah mendapatkan model terbaik, akan dilakukan peramalan kebutuhan infus NaCl 0,9% 500 ml dan infus glukosa 5% 500 ml di RSUP Sanglah untuk periode Juli 2017 sampai Desember 2017 yang hasil peramalannya dapat dilihat pada Tabel 4.
Tabel 4. Hasil Peramalan Kebutuhan Infus
|
No |
Bulan |
Jumlah Kebutuhan NaCl |
Jumlah Kebutuhan Glukosa |
|
1 |
Juli |
24.597 |
1.280 |
|
2 |
Agustus |
26.143 |
1.367 |
|
3 |
September |
26.850 |
1.406 |
|
4 |
Oktober |
25.605 |
1.406 |
|
5 |
November |
25.982 |
1.397 |
|
6 |
Desember |
25.654 |
1.393 |
|
Total |
154.831 |
8.249 | |
Data diolah : tahun 2017
Keakuratan Metode Peramalan
Kriteria metode peramalan yang digunakan untuk menguji keakuratan model adalah mean absolute percentage error (MAPE). Data actual yang digunakan dalam MAPE adalah data real pemakaian infus NaCl 0,9% 500 ml dan infus glukosa 5% 500 ml serta data hasil peramalan yang telah diperoleh. Nilai MAPE dari masing-masing data dapat dilihat pada Tabel 5.
Tabel 5. Nilai MAPE Masing-masing Data
|
No |
Infus |
MAPE |
|
1 |
NaCl 0,9% 500 ml |
14,341816% |
|
2 |
Glukosa 5% 500 ml |
9,685662% |
Data diolah : tahun 2017
Berdasarkan kriteria peramalan MAPE, terlihat bahwa model yang terpilih untuk meramalkan kebutuhan infus NaCl 0,9% 500 ml menghasilkan peramalan yang baik, sedangkan model yang terpilih untuk meramalkan kebutuhan infus glukosa 5% 500 ml menghasilkan peramalan yang akurat.
-
4. SIMPULAN DAN SARAN
Simpulan Penelitian
Berdasarkan pemaparan pada hasil dan pembahasan, model ARIMA terbaik yang digunakan untuk meramalkan kebutuhan infus NaCl 0,9% 500 ml adalah ARIMA (4,1,0) sedangkan model terbaik yang digunakan untuk meramalkan kebutuhan infus glukosa 5% 500 ml adalah model ARIMA (2,1,2). Adapun peramalan kebutuhan infus NaCl 0,9% 500 ml selama 6 bulan adalah sebanyak 154.831 unit sedangkan untuk infus glukosa 5% 500 ml adalah sebanyak 8.249 unit. Nilai MAPE dari kedua hasil peramalan tersebut adalah 14,341816% untuk infus NaCl 0,9% 500 ml dan 9,685662% untuk infus glukosa 5% 500 ml yang mengindikasikan kedua hasil tersebut adalah hasil peramalan dari model yang baik.
Saran
Saran untuk penelitian selanjutnya adalah untuk mengambil data bulanan lebih banyak, yaitu minimal data bulanan selama lima tahun untuk memperbesar akurasi peramalan. Selain itu jika terdapat pengaruh musiman pada data, peneliti selanjutnya diharapkan menggunakan metode peramalan seasonal autoregressive integrated moving average (SARIMA).
DAFTAR PUSTAKA
Gujarati, D., 2004. Basic Econometrics. New
York: McGraw-Hill.
Heizer, J., Render, B. & Munson, C., 2014.
Operations Management Sustainability and Supply Chain Management. New York: McGraw-Hill.
Makridakis, G., Wheelwright, C. & Hyndman, J., 1997. Forecasting: Methods and
Applications. United States of America: Wiley.
Wei, W., 2006. Time Series Analysis: Univariate and Multivariate Methods. New York: Pearson Addison Wesley.
Machmudin, Ali & Ulama, Brodjol S.S., 2012. Peramalan Temperatur Udara di Kota Surabaya dengan Menggunakan ARIMA dan Artificial Neural Network. Jurnal Sains dan Seni ITS, Volume 1, p. 118.
Zhang, T., Wang, K. & Zhang, X., 2015. Modelling and Analyzing the Transmission Dynamics of HBV Epidemic in Xinjiang, China. Plos One, 10(9), pp. 110-121.
133
Discussion and feedback