ANALISIS ALIRAN DARAH DALAM PEMBULUH ARTERI MENGGUNAKAN PERSAMAAN NAVIER-STOKES DAN METODE LATTICE-BOLTZMANN
on
E-Jurnal Matematika, Vol. 7 (2), Mei 2018, pp.102-110
DOI: https://doi.org/10.24843/MTK.2018.v07.i02.p191
ISSN: 2303-1751
ANALISIS ALIRAN DARAH DALAM PEMBULUH ARTERI MENGGUNAKAN PERSAMAAN NAVIER-STOKES DAN METODE LATTICE-BOLTZMANN
Fathurahman Ma’ruf Hudoarma1,∗ , P. H. Gunawan2, Aniq A. Rohmawati3
1Prodi Ilmu Komputasi, Fakultas Informatika – Universitas Telkom [Email:
fathurahmanmh@student.telkomuniversity.ac.id]
2Prodi Ilmu Komputasi, Fakultas Informatika - Universitas Telkom [Email: phgunawan@telkomuniversity.ac.id] 3Prodi Ilmu Komputasi, Fakultas Informatika - Universitas Telkom [Email:
aniqatiqi@telkomuniversity.ac.id] ∗ Corresponding Author
ABSTRACT
This simulation was performed to analyze arterial blood flow using Navier-Stokes equations and Lattice-Boltzmann method with Bhatnagar-Gross-Krook approach to obtain an explicit form of the Lattice-Boltzmann Bhatnagar-Gross-Krook equations. Then by adding some cases of plaque on simulation domain, changes in arterial blood flow pressure can be analyzed. The area and shape of the plaque cause narrowing the artery vessels that affect the pressure and rate of blood flow dynamically. The pressure of blood flow without plaque is stable ranged from 17 to 19 Pa. While in the vessels with plaque, blood flow pressure increased significantly up to 35.145 Pa.
Keywords: blood flow, bhatnagar-gross-krook, lattice-boltzmann method, navier-stokes equations.
pakan tekanan yang terjadi ketika jantung memompa darah untuk dialirkan keseluruh anggota tubuh. Tekanan darah dipengaruhi oleh aktifitas fisik dan waktu serta faktor lainnya seperti terjadinya pengendapan pada pembuluh arteri (Hall, 2015).
Simulasi aliran darah dilakukan dengan salah satu metode yang sukses dalam bidang simulasi gerakan fluida yaitu Metode Lattice-Boltzmann (LBM). Penggunaan metode LBM dalam simulasi aliran darah telah terbukti berhasil dilaksanakan sebelumnya (Abas et al., 2016; Boyd et al., 2004, 2007; Krafczyk et al., 1998). Metode LBM dibangun menggunakan model mikroskopik dan persamaan kinetik mesoskopik. Sebuah model kinetik yang disederhanakan disusun dari proses mikroskopik atau mesoskopik yang esensial sehingga hasil rata-rata makros-kopik yang dihasilkan dari model tersebut dapat memenuhi kriteria yang diharapkan. Pre-
mis dasar yang digunakan adalah bahwa pergerakan makroskopik fluida merupakan hasil kolektif dari partikel mikroskopik dalam suatu sistem dan pergerakan makroskopik fluida tidak sensitif terhadap fisis mikroskopik (Bensimon et al., 1986). Dalam hal ini, aliran darah yang mengalir dalam pembuluh arteri atau pembuluh yang besar dianggap sebagai fluida incompressible karena memiliki nilai densitas yang konstan terhadap waktu dan ruang sehingga persamaan fluida incompressible Navier-Stokes (NS) merupakan persamaan yang sesuai untuk memodelkan aliran darah. Kemudian dengan menurunkan persamaan Lattice-Boltzmann (LBE) menggunakan pendekatan Bhatnagar-Gross-Krook pada metode LBM sehingga didapatkan bentuk eksplisit dari persamaan Lattice-Boltzmann Bhatnagar-Gross-Krook (LBGK). Persamaan collision LBGK (Chen et al., 1991, 1992; Qian et al., 1992; Qian, 1990) telah digunakan dalam simulasi aliran darah Abas et al. (2016) dan pembentukan guncangan (Chu, 1965). Keunggulan metode LBM adalah proses penumbukan (collision) dan pengaliran (streaming) partikel mesoskopik yang berfungsi untuk simulasi fluida merupakan proses lokal dan diskrit sehingga lebih mudah diimplementasikan.
Topik permasalahan pada simulasi ini mengenai tekanan darah dalam pembuluh arteri dan daerah percabangan arteri dengan menggunakan persamaan NS dan metode LBM, serta analisa tekanan darah jika ditambahkan endapan pada pembuluh arteri dengan batasan simulasi hanya pada daerah percabangan pembuluh arteri yaitu brachiocephalic artery, right common carotid dan right subclavian.
Model matematis aliran darah dalam pembuluh arteri menggunakan persamaan NS dan metode LBM adalah dasar agar dapat diketahui hasil dari simulasi aliran darah. Hasil dari simulasi menunjukkan bagaimana tekanan aliran darah dalam pembuluh brachiocephalic artery dan pada daerah percabangan right common carotid artery dan right subclavian artery serta dengan ditambahkan bebera-
pa bentuk endapan pada brachiocephalic artery.
Densitas dalam fluida incompressible memiliki nilai yang konstan terhadap ruang dan waktu (Latt, 2008). Persamaan Navier-Stokes (NS) diatur oleh hukum kekekalan massa dan momentum yang menyatakan bahwa kecepatan adalah sebagai berikut.
V • u = 0 (1)
dengan u adalah kecepatan. Lalu, hukum kekekalan pada momentum mengarah ke persamaan NS berikut (Latt, 2008).
^u + (u ∙ V)u = — V p + ν V2u (2)
∂t
dengan p adalah tekanan, ν adalah viskositas kinematik dan t adalah satuan waktu.
Persamaan Lattice-Boltzmann (LBE) secara implisit adalah persamaan non-linier (Be-nzi et al., 1992). Istilah adveksi pada LBE dalam pendekatan makroskopik diubah dalam proses linier streaming dalam metode Lattice-Boltzmann (LBM).
LBM merupakan metode eksplisit yang tidak perlu menyelesaikan persamaan secara simultan setiap langkah waktu (Succi, 2001). Proses collision dan streaming merupakan proses lokal sehingga lebih mudah digunakan. Metode LBM menyimulasikan aliran incompressible berdasarkan kondisi bilangan Mach1 Ma = u/cs dengan u adalah kecepatan aliran fluida makroskopik dan cs adalah kecepatan suara serta variasi densitas (Chen et al., 1994). Terminologi umum yang digunakan dalam metode LBM adalah untuk merujuk pada 2 dimensi masalah dan 9 arah kecepatan kisi (lattice) dengan model D2Q9 (Mohamad, 2011) dapat dilihat seperti pada Gambar 1.
Persamaan LBE merupakan persamaan integro-differential. Permasalahan menyele-
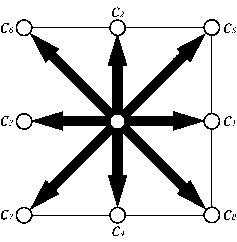
Gambar 1. Model Lattice-Boltzmann D2Q9.
saikan persamaan LBE adalah integral collision yang kompleks. Oleh karena itu, untuk menyelesaikan persamaan LBE digunakan pendekatan Bhatnagar-Gross-Krook (BGK) sehingga menjadi persamaan Lattice-Boltzmann Bhatnagar-Gross-Krook (LBGK) (Succi, 2001). Persamaan NS didapatkan dengan menurunkan persamaan LBE berikut (Mohamad, 2011).
fk(x + ck∆x, t + ∆t)= fk(x,t)+ Ωk(fk(x,t)), (3) (k = 0,1,..., N)
dengan fk (x, t) adalah fungsi distribusi kecepatan partikel, Ωk adalah operator collision, ck adalah vektor kecepatan (Frisch et al., 1986), ∆x dan ∆t adalah langkah spasial dan langkah waktu. Agar penulisan lebih sederhana, fk (x, t) akan ditulis sebagai fk.
Dalam Fisika pada gelombang panjang dan frekuensi rendah, langkah spasial dan langkah waktu pada Persamaan (3) dapat dianggap sebagai parameter kecil (ε) dengan orde yang sama. Dengan melakukan ekspansi Taylor dalam ruang dan waktu pada Persamaan (3), maka didapat bentuk kontinum2 orde ke-dua ε seperti berikut (Chen and Doolen, 1998).
Ωk ε
f+ck'vλ
+ ε (2 v. fk
(4)
v dfk, 1 d 2 fk \
+ck ■v ^ + 2 *T)
Untuk mendapatkan persamaan hidrodi-namika makroskopis, digunakan ekspansi Chapman-Enskog yang pada dasarnya merupakan ekspansi formal multiscaling (Frisch et al., 1986). Satu partikel fungsi distribusi fk dapat diperluas secara formal mengenai fungsi distribusi ekuilibrium fkeq sehingga,
f k = f eq + εfkq (5)
dengan fneq = f^ + εf(2 + O(ε2) adalah fungsi distribusi non-ekuilibrium.
Selanjutnya, dengan mensubtitusikan f pada Persamaan (5) ke dalam operator collision Ω dalam Persamaan (4) ketika ε → 0 maka Ωk(fkq) = 0 (Chen and Doolen, 1998). Hal ini menunjukan operator collision diline-arkan (Higuera and Jimenez, 1989) untuk collision konservasi massa dan momentum (Be-nzi et al., 1992) pada tahap collision LBGK (Bhatnagar et al., 1954) sehingga,
Ω = -1 fneq = - ^ (fk1’+ fk2’) (6)
ε τ ετ
kemudian didapat bentuk eksplisit dari persamaan LBGK pada Persamaan (3) seperti berikut.
fk - feq
f k (x + ∆x, t + ∆t) = f k (x, t)--τ— (7)
Persamaan Navier-Stokes memiliki orde dua non-linier. Bentuk umum fungsi distribusi ekuilibrium dapat ditulis sampai O(u2) sehingga diperoleh secara analitis sebagai berikut (Chen et al., 1992; Qian et al., 1992).
feeq = ρWk [1 + 3Ck • u + 2 (Ck ■ u)2 - 2u2] (8)
dengan besaran wk adalah sebagai berikut.
Wk =
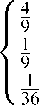
, k = 0
, k = 1,2,3,4 (9)
, k = 5,6,7,8
Sehingga persamaan momentum yang diha-
silkan sama persis dengan persamaan Navier-Stokes jika variasi densitas δρ memiliki nilai yang kecil (Qian and Orszag, 1993).
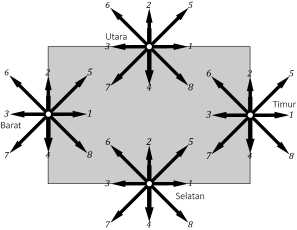
Gambar 2. Model fungsi distribusi pada batas
Model fungsi distribusi pada batas domain dapat dilihat seperti pada Gambar 2. Batas yang diaplikasikan pada batas barat atau sebelah kiri domain yang merupakan tempat masuknya aliran darah pada domain simulasi adalah batas dengan diketahuinya besar kecepatan. Pada batas timur atau sebelah kanan domain merupakan tempat keluarnya aliran darah dari domain simulasi disebut juga sebagai outlet extrapolation. Kondisi batas bounce back merupakan cara untuk membuat dinding yang bersifat solid, sehingga partikel dapat memantul tanpa kehilangan momentum ketika menumbuk dinding pembuluh (Mohamad, 2011).
Hasil simulasi aliran darah dalam pembuluh arteri menggunakan persamaan NS dan metode LBM disajikan secara horizontal, sehingga darah akan mengalir dari kiri ke kanan dalam satu kali detakkan jantung.
Gambar 3 menunjukan bahwa aliran darah masuk dengan tekanan maksimum 20.049 Pa dan keluar dengan tekanan maksimum 3.894 Pa pada cabang common carotid dan 8.928 Pa pada cabang subclavian.
Pada Gambar 4 ditambahkan endapan di-bagian atas dan bawah domain simulasi dengan luas 32 mm2. Aliran darah masuk dengan tekanan maksimum 12.745 Pa dan keluar dengan tekanan maksimum 5.604 Pa pada cabang common carotid dan 10.328 Pa pada cabang subclavian.
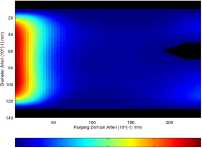
(a) Aliran darah pada waktu t = 5 × 10-6 s.
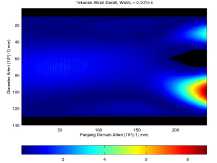
(b) Aliran darah pada waktu t = 1500 × 10-6 s.
Gambar 3. Aliran darah tanpa endapan pada waktu t = 5 × 10-6 s dan t = 1500 × 10-6 s.
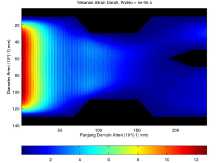
(a) Aliran darah pada waktu t = 5 × 10-6 s.
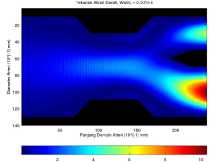
(b) Aliran darah pada waktu t = 1500 × 10-6 s.
Gambar 4. Aliran darah dengan luas endapan 32 mm2 pada waktu t = 5 × 10-6 s dan t = 1500 × 10-6 s.
Dengan menambahkan panjang dari endapan pada Gambar 4 sehingga endapan memiliki luas 60 mm2 seperti pada Gambar 5 aliran darah masuk dengan tekanan maksimum 11.005 Pa dan keluar dengan tekanan maksimum 5.660 Pa pada cabang common carotid dan 10.178 Pa pada cabang subclavian.
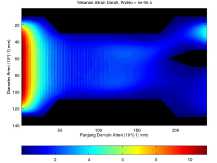
(a) Aliran darah pada waktu t = 5 × 10-6 s.
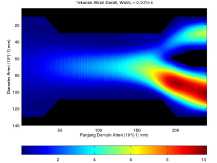
(b) Aliran darah pada waktu t = 1500 × 10-6 s.
Gambar 5. Aliran darah dengan luas endapan 60 mm2 pada waktu t = 5 × 10-6 s dan t = 1500 × 10-6 s.
Kemudian menambahkan tinggi dari endapan pada Gambar 5 sehingga endapan memiliki luas 90 mm2 seperti pada Gambar 6
aliran darah masuk dengan tekanan maksimum 10.688 Pa dan keluar dengan tekanan maksimum 4.417 Pa pada cabang common carotid dan 11.061 Pa pada cabang subclavian.
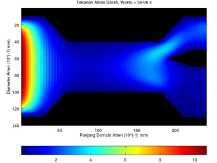
(a) Aliran darah pada waktu t = 5 × 10-6 s.
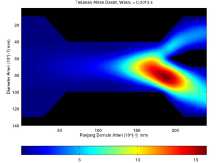
(b) Aliran darah pada waktu t = 1500 × 10-6 s.
Gambar 6. Aliran darah dengan luas endapan 90 mm2 pada waktu t = 5 × 10-6 s dan t = 1500 × 10-6 s.
Dengan melihat Gambar 3, 4, 5 dan 6, dapat diketahui bahwa keempat gambar tersebut memiliki perbedaan. Aliran darah yang ditambahkan endapan cenderung mengalir lebih lambat, membuktikan bahwa semakin besar endapan dalam pembuluh darah, aliran darah mengalir semakin lambat. Adapun hasil yang diambil pada waktu t = 750 × 10-6 s dapat dilihat pada Gambar 7.
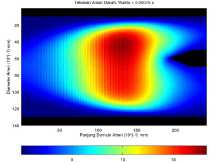
(a) Aliran darah tanpa endapan.
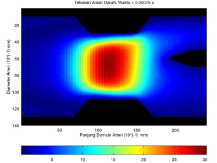
(b) Aliran darah dengan luas endapan 32 mm2.
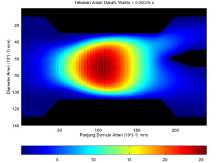
(c) Aliran darah dengan luas endapan 60 mm2.
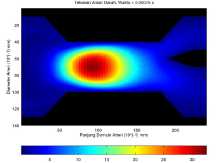
(d) Aliran darah dengan luas endapan 90 mm2.
Gambar 7. Kondisi aliran darah dalam pembuluh arteri pada waktu t = 750 × 10-6 s.
Gambar 7a menunjukan bahwa aliran da-
rah dalam posisi ini memiliki tekanan maksimum 18.279 Pa. Tekanan maksimum didominasi pada kordinat (45,130) yang seolah-olah aliran darah dengan tekanan maksimum akan mengarah ke cabang common carotid yang memiliki diameter lebih kecil daripada cabang subclavian. Kemudian pada Gambar 7b, 7c dan 7d menunjukan bahwa endapan menyebabkan tekanan darah dalam pembuluh cenderung lebih tinggi. Tekanan darah maksimum pada Gambar 7b berada pada kordinat (66,114) dengan nilai 30.282 Pa. Sedangkan pada Gambar 7c yang terdapat endapan lebih luas daripada Gambar 7b hanya memiliki tekanan maksimum 25.777 Pa yang berada pada kordinat (71,104). Lalu pada Gambar 7d menunjukan bahwa tekanan maksimum pada aliran darah sebesar 32.544 Pa yang berada pada kordinat (71,92).
Dalam setiap kasus yaitu pembuluh darah tanpa endapan dan dengan endapan, tekanan darah maksimum terdapat pada waktu t yang berbeda. Tekanan darah maksimum ini dapat dilihat pada Gambar 8.
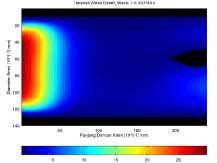
(a) Tanpa endapan pada waktu t = 145 × 10-6 s.
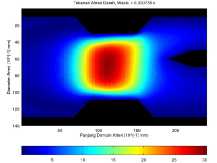
(b) Endapan 32 mm2 pada waktu t = 735 × 10-6 s.

(c) Endapan 60 mm2 pada waktu t = 420 × 10-6 s.
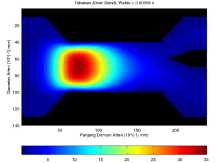
(d) Endapan 90 mm2 pada waktu t = 580 × 10-6 s.
Gambar 8. Kondisi tekanan maksimum aliran darah dalam setiap kasus.
Gambar 8 menunjukan kondisi tekanan maksimum dalam pembuluh darah pada setiap kasusnya dengan waktu t yang berbeda.
Pada Gambar 8a, tekanan maksimumnya sebesar 29.530 Pa ketika aliran darah memasuki domain simulasi. Kemudian dalam Gambar 8b tekanan darah maksimumnya sebesar 30.339 Pa ketika aliran darah sesaat setelah memasuki daerah endapan. Sedangkan pada Gambar 8c dan 8d tekanan darah maksimum yang dihasilkan masing-masing sebesar 31.401 Pa dan 35.145 Pa ketika aliran darah tepat memasuki daerah endapan.
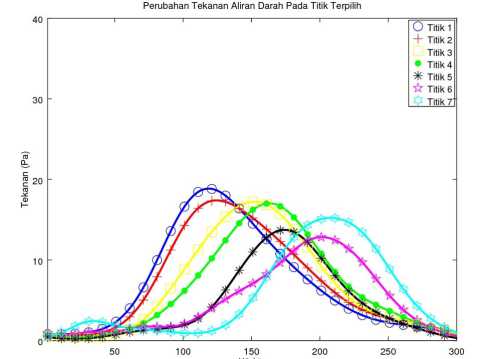
(a) Perubahan tekanan tanpa endapan.

Gambar 9. Tujuh titik kordinat terpilih.
Kemudian dengan tujuh titik terpilih seperti pada Gambar 9 untuk mengamati aliran darah, maka didapat hasil seperti pada Gambar 10.
Gambar 10 menunjukan perubahan tekanan darah terhadap waktu. Setiap titik terpilih memiliki nilai tekanan maksimum yang berbeda dan pada waktu yang berbeda. Titik yang berada di daerah percabangan yaitu titik 5, 6 dan 7 memiliki tekanan lebih rendah dari titik sebelumnya. Hal ini menunjukan bahwa tekanan aliran darah pada percabangan hingga keluar dari domain simulasi mengalami penurunan tekanan.
Dari pengujian yang telah dilakukan berdasarkan Gambar 3, 4, 5, 6, 7 dan 8 didapat hasil seperti pada Tabel 1.
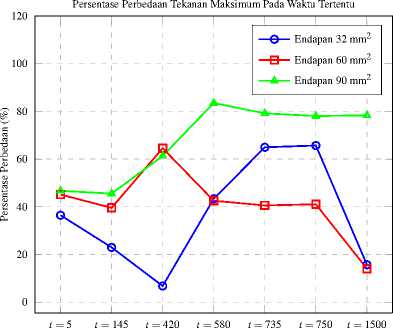
Tabel 1 menunjukan bahwa tekanan aliran darah meningkat pada daerah endapan dan menurun ketika keluar dari daerah endapan sama halnya pada daerah percabangan di akhir simulasi. Kemudian dengan menghitung persentase perbedaan dari nilai tekanan maksimum terhadap kasus tanpa endapan didapat hasil seperti Gambar 11.
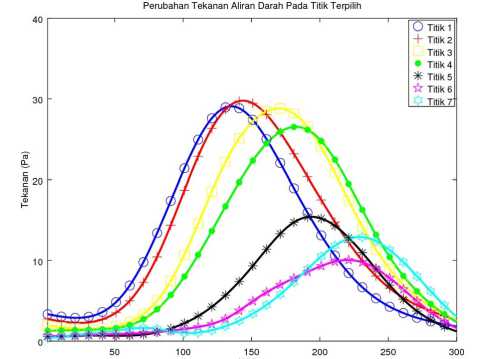
(b) Perubahan tekanan dengan endapan 32 mm2.
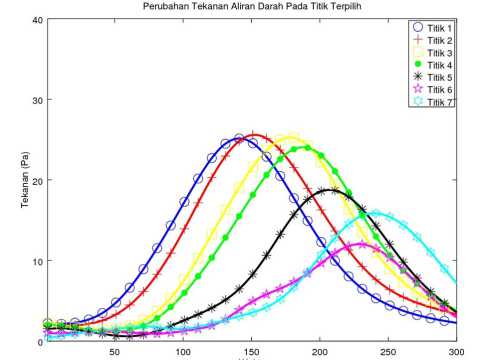
(c) Perubahan tekanan dengan endapan 60 mm2.
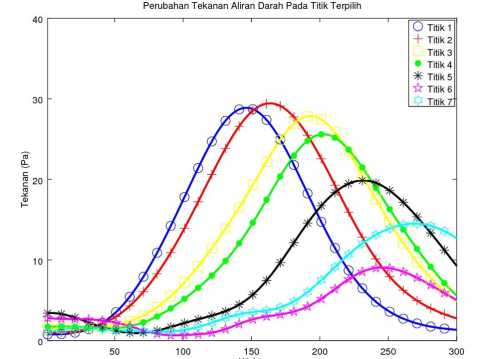
(d) Perubahan tekanan dengan endapan 90 mm2.
Gambar 10. Perubahan tekanan darah pada tujuh titik dari waktu t = 5 × 10-6 s hingga t = 1500 × 10-6 s.
Tabel 1. Tekanan darah maksimum dalam waktu (10 6 s)
|
Tekanan maksimum (Pa) | ||||||||
|
t |
5 |
145 |
420 |
580 |
735 |
750 |
1500 |
Rata-rata |
|
Tanpa endapan |
20.049 |
29.530 |
19.083 |
19.155 |
18.395 |
18.279 |
8.928 |
19.060 |
|
Endapan 32 mm2 |
12.745 |
22.755 |
20.375 |
27.454 |
30.339 |
30.282 |
10.328 |
22.040 |
|
Endapan 60 mm2 |
11.005 |
17.854 |
31.401 |
27.299 |
25.853 |
25.777 |
10.178 |
21.338 |
|
Endapan 90 mm2 |
10.688 |
16.093 |
30.778 |
35.145 |
32.957 |
32.544 |
15.920 |
24.875 |
Tabel 2. Tekanan darah maksimum pada tujuh titik terpilih.
|
Kasus |
Tekanan maksimum (Pa) | |||||||
|
Titik 1 |
Titik 2 |
Titik 3 |
Titik 4 |
Titik 5 |
Titik 6 |
Titik 7 |
Rata-rata | |
|
Tanpa endapan |
18.855 |
17.396 |
17.232 |
17.027 |
13.736 |
12.835 |
15.218 |
16.043 |
|
Endapan 32 mm2 |
29.068 |
29.766 |
28.800 |
26.517 |
15.420 |
10.055 |
12.916 |
21.792 |
|
Endapan 60 mm2 |
25.139 |
25.583 |
25.260 |
24.050 |
18.757 |
12.014 |
15.850 |
20.950 |
|
Endapan 90 mm2 |
28.881 |
29.434 |
27.858 |
25.594 |
19.865 |
9.052 |
14.510 |
22.170 |
Waktu (10-6 s)
Persentase Perbedaan Tekanan Maksimum Pada Titik Terpilih
Titik Terpilih
Gambar 11. Persentase perbedaan tekanan maksimum pada waktu tertentu terhadap kasus tanpa endapan
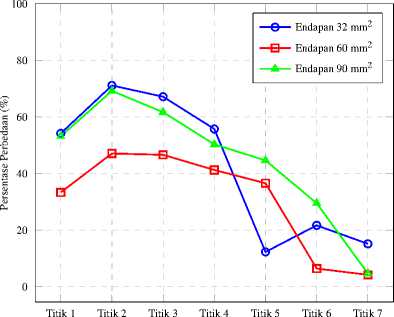
Gambar 12. Persentase perbedaan tekanan maksimum setiap titik terpilih terhadap kasus tanpa endapan.
Gambar 11 menunjukan bahwa perbedaan tekanan maksimum didominasi oleh kasus endapan dengan luas 90 mm2, sama halnya dengan persentase perbedaan paling tinggi yang terletak pada waktu t = 420 × 10-6 s sebesar 83%. Kemudian berdasarkan Gambar 10, tekanan darah maksimum pada setiap titik dapat dilihat pada Tabel 2.
Tabel 2 menunjukan tekanan maksimum dan rata-rata dari setiap titik terpilih. Rata-rata tekanan maksimum tertinggi berada pada kasus endapan dengan luas 90 mm2. Persentase perbedaan terkanan maksimumnya dapat dilihat pada Gambar 12.
Pada Gambar 12, perbedaan tekanan maksimum tertinggi yaitu berada di titik 2 pada kasus endapan dengan luas 32 mm2 sebesar 71%. Sedangkan secara keseluruhan, perbedaan tekanan maksimum tertinggi berada pada kasus endapan dengan luas 90 mm2. Hal ini dikarenakan pada endapan 32 mm2 dan 60 mm2 terdapat penurunan tekanan yang signifikan.
Model aliran darah dalam pembuluh arteri didapatkan menggunakan persamaan Navier-Stokes dan metode Lattice-Boltzmann de-
ngan pendekatan Bhatnagar-Gross-Krook sehingga aliran darah dapat disimulasikan dan dianalisa. Tekanan aliran darah pada daerah percabangan right common carotid artery dan right subclavian hingga keluar dari domain simulasi mengalami penurunan. Dalam kasus tanpa endapan, aliran darah mengalami penurunan tekanan hingga 6.020 Pa. Sedangkan dalam kasus dengan endapan, penurunan tekanan aliran darah mencapai 20.714 Pa. Dalam kasus tanpa endapan, tekanan aliran darah pada pembuluh brachiocephalic artery berkisar 17-19 Pa secara stabil. Sedangkan pada kasus dengan endapan, tekanan aliran darah meningkat secara signifikan ketika aliran darah memasuki daerah endapan hingga 35.145 Pa. Luas dan bentuk endapan mempersempit rongga pembuluh arteri sehingga endapan dapat mempengaruhi tekanan dan laju aliran darah secara dinamis.
Persamaan Navier-Stokes dan metode Lattice-Boltzmann yang digunakan dalam simulasi dapat dilakukan dengan pendekatan lain seperti Regularized BGK Model (Latt and Chopard, 2006) dan Multiple Relaxation Time Model (Premnath and Abraham, 2007) agar hasil simulasi dapat dibandingkan.
Daftar Pustaka
Abas, A., Mokhtar, N. H., Ishak, M., Abdullah, M., and Ho Tian, A. (2016). Lattice boltzmann model of 3d multiphase flow in artery bifurcation aneurysm problem. Computational and mathematical methods in medicine, 2016.
Bensimon, D., Kadanoff, L. P., Liang, S., Shraiman, B. I., and Tang, C. (1986). Viscous flows in two dimensions. Reviews of Modern Physics, 58(4):977.
Benzi, R., Succi, S., and Vergassola, M. (1992). The lattice boltzmann equation: theory and applications. Physics Reports, 222(3):145–197.
Bhatnagar, P. L., Gross, E. P., and Krook, M. (1954). A model for collision processes in gases. i. small amplitude processes
in charged and neutral one-component systems. Physical review, 94(3):511.
Boyd, J., Buick, J., Cosgrove, J., and Stansell, P. (2004). Application of the lattice boltzmann method to arterial flow simulation: investigation of boundary conditions for complex arterial geometries. Australasian Physical & Engineering Science in Medicine, 27(4):207–212.
Boyd, J., Buick, J. M., and Green, S. (2007). Analysis of the casson and carreau-yasuda non-newtonian blood models in steady and oscillatory flows using the lattice boltzmann method. Physics of Fluids, 19(9):093103.
Chen, H., Chen, S., and Matthaeus, W. H. (1992). Recovery of the navier-stokes equations using a lattice-gas boltzmann method. Physical Review A, 45(8):R5339.
Chen, S., Chen, H., Martnez, D., and Mattha-eus, W. (1991). Lattice boltzmann model for simulation of magnetohydrodynamics. Physical Review Letters, 67(27):3776.
Chen, S. and Doolen, G. D. (1998). Lattice boltzmann method for fluid flows. Annual review of fluid mechanics, 30(1):329–364.
Chen, Y., Ohashi, H., and Akiyama, M. (1994). Thermal lattice bhatnagar-gross-krook model without nonlinear deviations in macrodynamic equations. Physical Review E, 50(4):2776.
Chu, C. (1965). Kinetic-theoretic description of the formation of a shock wave. The Physics of Fluids, 8(1):12–22.
Frisch, U., d’Humieres, D., Hasslacher, B., Lallemand, P., Pomeau, Y., and Rivet, J.-P. (1986). Lattice gas hydrodynamics in two and three dimensions. Technical report, Los Alamos National Lab., NM (USA); Observatoire de Nice, 06 (France); Ecole Normale Superieure, 75-Paris (France).
Hall, J. E. (2015). Guyton and Hall textbook of medical physiology e-Book. Elsevier Health Sciences.
Succi, S. (2001). The lattice Boltzmann equation: for fluid dynamics and beyond. Oxford university press.
Higuera, F. and Jimenez, J. (1989). Boltzmann approach to lattice gas simulations. EPL (Europhysics Letters), 9(7):663.
Krafczyk, M., Cerrolaza, M., Schulz, M., and Rank, E. . (1998). Analysis of 3d transient blood flow passing through an artificial aortic valve by lattice–boltzmann methods. Journal of Biomechanics, 31(5):453–462.
Latt, J. (2008). Choice of units in lattice boltzmann simulations. Freely available online at http://lbmethod. org/ media/howtos: lbunits. pdf.
Latt, J. and Chopard, B. (2006). Lattice boltzmann method with regularized precollision distribution functions. Mathematics and Computers in Simulation, 72(2-6):165–168.
Mohamad, A. A. (2011). Lattice Boltzmann method: fundamentals and engineering applications with computer codes. Springer Science & Business Media.
Premnath, K. N. and Abraham, J. (2007). Three-dimensional multi-relaxation time (mrt) lattice-boltzmann models for multiphase flow. Journal of Computational Physics, 224(2):539–559.
Qian, Y., d’Humie` res, D., and Lallemand, P. (1992). Lattice bgk models for navier-stokes equation. EPL (Europhysics Letters), 17(6):479.
Qian, Y. and Orszag, S. (1993). Lattice bgk models for the navier-stokes equation: Nonlinear deviation in compressible regimes. EPL (Europhysics Letters), 21(3):255.
Qian, Y. H. (1990). Lattice gas and lattice kinetic theory applied to the navier-stokes equations. Doktorarbeit, Universite Pierre et Marie Curie, Paris.
110
Discussion and feedback