KONVERGENSI NUMERIK FLUKS RUSANOV DAN HLLE PADA METODE BEDA VOLUM UNTUK MENGHAMPIRI PERSAMAAN AIR DANGKAL
on
E-Jurnal Matematika, Vol. 7 (2), Mei 2018, pp.94-101
DOI: https://doi.org/10.24843/MTK.2018.v07.i02.p190
ISSN: 2303-1751
KONVERGENSI NUMERIK FLUKS RUSANOV DAN HLLE PADA METODE BEDA VOLUME UNTUK MENGHAMPIRI PERSAMAAN AIR DANGKAL
Eko Meidianto N. R.1,∗, P. H. Gunawan2, A. Atiqi Rohmawati3
1Prodi Ilmu Komputasi, Fakultas Informatika – Universitas Telkom [Email:
ekomeidianto@student.telkomuniversity.ac.id]
2Prodi Ilmu Komputasi, Fakultas Informatika – Universitas Telkom [Email: phgunawan@telkomuniversity.ac.id] 3Prodi Ilmu Komputasi, Fakultas Informatika – Universitas Telkom [Email: aniqatiqi@telkomuniversity.ac.id] ∗ Corresponding Author
ABSTRACT
This one-dimensional simulation is performed to find the convergence of different fluxes on the water wave using shallow water equation. There are two cases where the topography is flat and not flat. The water level and grid of each simulation are made differently for each case, so that the water waves that occur can be analyzed. Many methods can be used to approximate the shallow water equation, one of the most used is the finite volume method. The finite volume method offers several numerical solutions for approximate shallow water equation, including Rusanov and HLLE. The derivation result of the numerical solution is used to approximate the shallow water equation. Differences in numerical and topographic solutions produce different waves. On flat topography, the Rusanov flux has an average error 0.06403 and HLLE flux with an average error 0.06163. While the topography is not flat, the rusanov flux has a 1.63250 error and the HLLE flux has an error of 1.56960.
Keywords: shallow water equation, finite volume method, convergence, topography, rusanov, harten-lax-van leer-einfeldt.
Beberapa solusi fluks numerik telah dipaparkan seperti Riemann flux, Lax–Friedrichs approximation, Roe scheme, Engquist–Osher, Harten–Lax–van Leer (HLLE) flux functions, atau Rusanov flux (Bassi and Rebay, 1997). Namun jurnal ini akan memaparkan perhitungan secara numerik dengan metode beda volume menggunakan fluks Rusanov dan Harten-Lax-van Leer-Einfeldt (HLLE) untuk mendekati nilai dari persamaan air dangkal. Persamaan air dangkal juga terkenal dengan nama Saint-Venant yang merupakan sistem dua persamaan simultan yang terdiri atas hukum kekekalan momentum dan hukum kekekalan massa (Doyen and Gunawan, 2014; Mungkasi, 2011).
Batasan-batasan yang dikerjakan dalam jurnal ini antara lain, topografi dibuat dengan
dua kondisi yaitu datar dan tidak datar, ketinggian permukaan air juga dibuat berbeda untuk setiap topografi, kecepatan awal air diatur sama, dan batas (boundary) kanan dan kiri untuk setiap simulasi menggunakan dirichlet boundary. Simulasi ini dibangun untuk membandingkan hasil perhitungan solusi numerik untuk mendekati solusi reference dari persamaan air dangkal (SWE). Selain itu, dilakukan perhitungan konvergensi antara solusi numerik yang diterapkan terhadap solusi reference. Solusi reference diperoleh dari hasil simulasi menggunakan fluks HLLE dengan pembagian sel sebanyak 3200.
-
2 METODE PENELITIAN
-
2.1 Persamaan Air Dangkal
-
Persamaan air dangkal atau shallow water equation (SWE) juga terkenal dengan nama Saint-Venant yang merupakan sistem dua persamaan simultan yang terdiri atas hukum kekekalan momentum dan hukum kekekalan massa (Doyen and Gunawan, 2014; Mungka-si, 2011), yang diberikan sebagai berikut.
dimana U adalah vektor permukaan air, F adalah pengatur fluks, dan Sb adalah vektor pembentuk dasar permukaan air.
-
2.2 Topografi
Topografi dibuat dengan dua kondisi, yaitu datar (flat bottom) dan tidak datar (terdapat tonjolan pada bagian tertentu). Untuk lebih jelas dapat dilihat pada Gambar 1 dan Gambar 2.
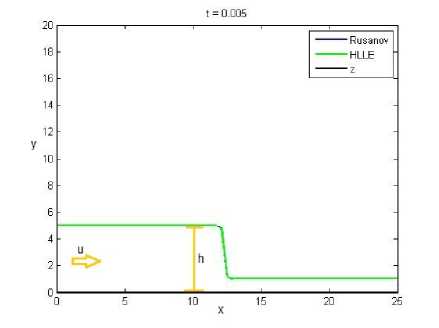
Gambar 1. Kondisi awal (t = 0) dengan topografi datar (z = 0)
ht + (hu) x = 0 I (1)
(hu) t + (hu2 + 2 gh2) x = - ghzχ
dimana h adalah ketinggian air, u adalah kecepatan air, z adalah tinggi dasar permukaan air (topografi), dan g adalah percepatan gravitasi dengan nilai 9.8 m/s2. Pada bentuk vektor persamaan air dangkal (1) dapat ditulis sebagai berikut.
(2)
Pada Gambar 1 terlihat dasar permukaan adalah datar (z = 0) dengan tinggi permukaan h = 7 jika x < LL (L adalah panjang total domain terhadap sumbu x) dan h = 3 untuk kondisi lainnya, sehingga Persamaan (1) bersifat homogen. Karenanya, akan diperoleh sistem konservasi sebagai berikut.
( ht + (hu)χ = 0 (6)
[ (hu)t + (hu2 + 2gh2)χ = 0
U=
h hu
(3)
F (U ) =
hu
hu2 + 2gh2
Sb t"gh ∂x]
(4)
(5)
Sedangkan pada Gambar 2 dasar permukaan tidak datar (z = 0) dengan tinggi permukaan air h = 10. Untuk inisial z dapat dilihat pada Persamaan (7). Sedangkan untuk sistem konservasinya dapat dilihat pada Persamaan (8).
z=
1 if 12.5 > x > 235
0 Lainnya
(7)
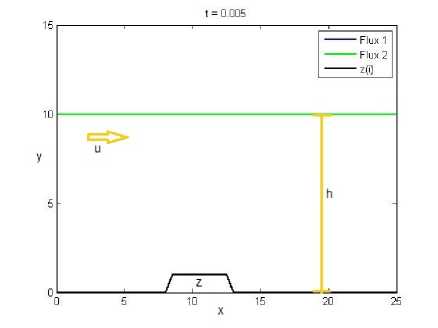
Gambar 2. Kondisi awal (t = 0) dengan topografi tidak datar (z = 0)
2.3.1 Fluks Rusanov
Pendekatan nilai fluks F± i (9) menggunakan solusi numerik Rusanov adalah sebagai berikut (Audusse et al., 2000; Botta et al., 2004; Klein et al., 2001).
Ftt 2 = f (ULUR ) = F UL l + F (UR) — U+ (10) dimana c merupakan kecepatan gelombang dengan nilai sebagai berikut.
c = maks
ζ UL ± ^ghm0d
, UR ± ^ghhmP
(11)
(8)
ht + (hu) χ = 0
(hu) t + (hu2 + 2 gh2) χ + ghzχ = 0
Kondisi awal pada Gambar 1 dan Gambar 2 berlaku untuk fluks Rusanov dan HLLE.
-
2.3 Model Numerik
Pada jurnal ini, untuk menghampiri persamaan air dangkal digunakan metode beda volume dengan fluks Rusanov dan HLLE sebagai solusi numerik, yang akan didiskritkan berdasarkan waktu dan ruang dengan domain Ω = (0, L). Berikut adalah bentuk diskrit dari persamaan air dangkal (2) (Audusse et al., 2004; Hu et al., 2012).
Un+1 = Un—δx ( f+2 — F-2)+δSb (9)
dimana ∆t adalah langkah waktu, dan ∆x adalah langkah spasial. Nilai Uin mewakili nilai pendekatan rata-rata pada interval xi dan pada waktu tn. Notasi F± 1 digunakan sebagai pendekatan untuk rata-rata flux di titik x = xi± 2.
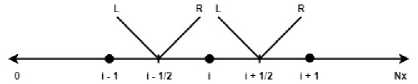
Gambar 3. Ilustrasi diskritisasi pada domain L menjadi Nx bagian
Pada saat mencari nilai c terdapat notasi hmod yaitu variabel ketinggian air baru, yang merupakan hasil modifikasi dari ketinggian air (h) dan topografi (z). Modifikasi ini dilakukan untuk mendapatkan skema keseimbangan yang sederhana dan cepat dari fluks numerik tertentu untuk masalah homogen. Modifikasi antara h dan z ini disebut Reconstruct on Scheme yang mengacu pada (Audusse et al., 2004; Bouchut, 2004). Notasi R adalah nilai sebelah kanan dari indeks yang dicari dan L adalah nilai sebelah kiri dari indeks yang dicari (Gambar 3).
hmod = maks (0, hR + min (0, ∆ z)) (.^
hmod = maks (0, hL — maks (0, ∆ z))
∆z± = ZR — ZL (13)
-
2.3.2 Fluks HLLE (Harten-Lax-van
Leer-Einfeldt)
Perhitungan numerik menggunakan fluks HLLE berbeda dengan fluks Rusanov. Untuk mendekati nilai F± 1 menggunakan solusi numerik HLLE adalah sebagai berikut (Bassi and Rebay, 1997; Quirk, 1997).
F± 2 = 11F (Ur )+12 F (Ul ) — t3(Ur — Ul ) (14)
dimana nilai t1, t2, dan t3 berturut-turut adalah.
min (c2,0) - min (c 1,0)
t 1 =----------------------- (15)
c2 - c1
12 = 1-11 (16)
C2∣C 1|- C 1|C2∣ 2(C2 - C1)
(17)
dengan c1 dan c2 adalah kecepatan gelombang. Pada solusi numerik fluks HLLE persamaan kecepatan gelombang adalah sebagai berikut.
-
3 HASIL DAN PEMBAHASAN
Pada simulasi dilakukan uji numerik vacuum occurrence yang berdasar pada usulan E. F. Toro (Goutal and Maurel, 1997). Namun pada makalah ini tidak membahas tentang skema numerik untuk menghitung va-cum occurrence. Berdasar pada (Galloue¨t et al., 2003), inisial awal untuk panjang total domain Ω(0, L) adalah 25, kecepatan aliran air hu = -350 jika x < 50/3 dan hu = 350 untuk kondisi lainnya, waktu akhir adalah t = 0.05, dan pembagian sel (Nx) pada domain Ω(0, L) adalah 100, 200, 400, 800, dan 1600. Sedangkan untuk tinggi permukaan air (h) dan topografi (z) untuk masing-masing kasus telah disebutkan sebelumnya (pada bagian topografi).
Ur - 2 JghR0 min (uL — Jmod0, u * - √ gh *)
if hL = 0
if hL > 0
(18)
uL - 2, g~hm°0 if hR = 0
c 2 = JJL (19)
I min ( Ur - U ghRod, u * - y/ gh *) il hR > 0
Pada saat mencari nilai c1 dan c2 terdapat variabel hmod yang merupakan variabel ketinggian air hasil modifikasi dan telah dijelaskan pada bagian 2.3.1. Perlu diketahui ketika menghampiri persamaan air dangkal menggunakan fluks Rusanov dan fluks HLLE, ketinggian air yang digunakan adalah ketinggian air hasil modifikasi (hmod). Selain itu terdapat variabel u * (kecepatan air) dan h. * (ketinggian air) yang sudah dimodifikasi. Variabel u* dan h* hanya digunakan saat mencari nilai c1 dan c2. Berikut adalah persamaan untuk mencari nilai dari u* dan h* .
3.1 Topografi Tidak Datar
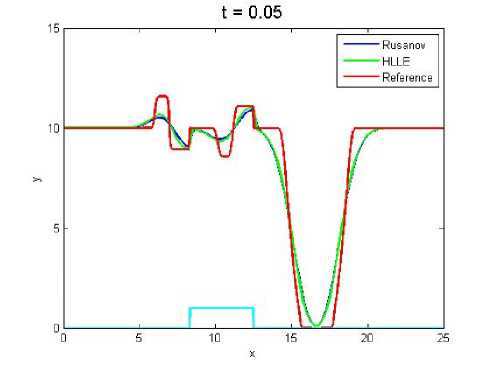
Gambar 4. (Nx = 100)
u* = 2 ( Ul + UR) + ghmod- - gRod- (20)
h*
(
Jgod- - Jghmo
2
×
ul - ur 4
}
2
g
(21)
Hasil simulasi yang dilakukan dapat dilihat pada Gambar 4 sampai 8. Saat mengamati Gambar 4 sudah terlihat bahwa fluks HLLE lebih mendekati fluks reference daripada fluks Rusanov. Perbedaan ini terlihat lebih jelas pada lekukan gelombang. Pada Gambar 5 dan 6 mulai terlihat bahwa gelombang yang dihasilkan fluks HLLE dan Rusanov lebih mendekati fluks refernce dibanding pada Gambar 4, begitupun pada Gambar 7. Sedangkan pada Gambar 8 fluks Rusanov dan HLLE hampir mendekati fluks reference secara sempurna dan fluks HLLE tetap yang paling mendekati. Perbedaan pendekatan pada
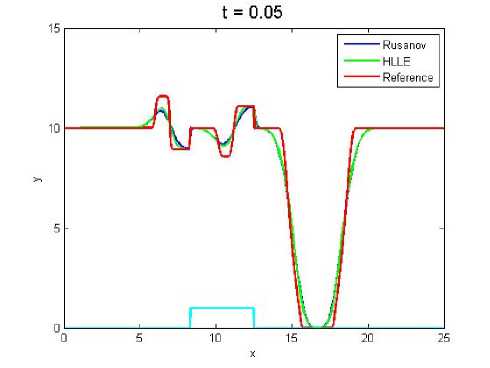
Gambar 5. (Nx = 200)
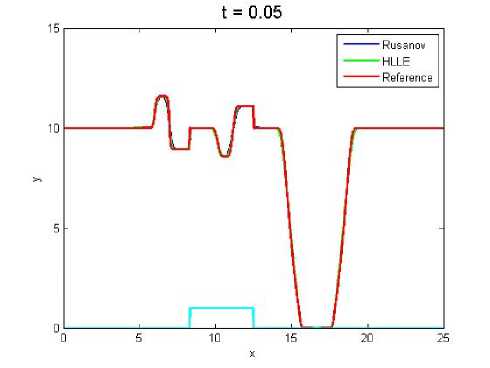
Gambar 8. (Nx = 1600)
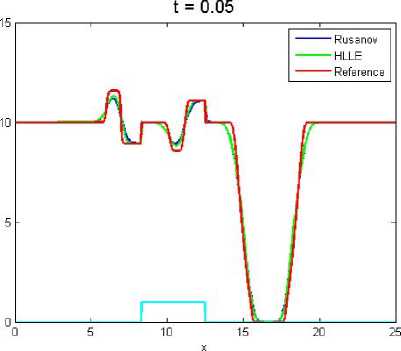
Gambar 6. (Nx = 400)
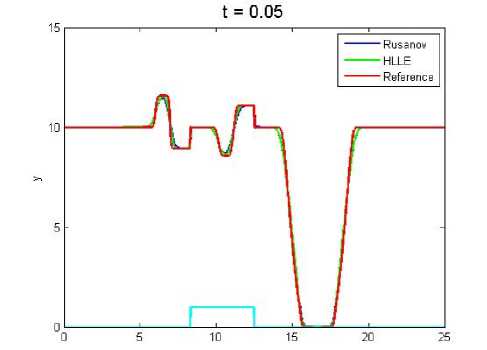
Gambar 7. (Nx = 800)
Gambar 4 sampai Gambar 8 disebabkan oleh pembagian sel (grid) yang berbeda-beda.
Tabel 1 menunjukkan konvergensi dan error ketinggian air (h) secara numerik dari solusi numerik terhadap solusi reference pada waktu akhir (t = 0.05). Pada tabel tersebut dapat dilihat bahwa error fluk HLLE lebih kecil dibandingkan fluks Rusanov, dengan rata-rata error 0.06403 untuk fluks Rusanov dan 0.06163 untuk fluks HLLE. Pembagian sel (Nx) pada saat simulasi ternyata mempengaruhi error dari setiap solusi numerik baik Rusanov maupun HLLE. Simulasi dengan Nx = 100 memiliki error yang lebih besar daripada simulasi dengan Nx = 200. Be-gitupun simulasi dengan Nx = 200 memiliki error yang lebih besar dari simulasi dengan Nx = 400, dan seterusnya. Hal tersebut sesuai dengan hasil simulasi yang dilakukan bahwa fluks HLLE lebih mendekati fluks reference dibanding fluks Rusanov. Sedangkan konvergensi untuk setiap fluks sama yaitu menuju satu. Error diperoleh dari selisih antar solusi numerik dan solusi reference dikalikan dengan ∆x (∆x = NLx.). Sedangkan tingkat konvergensi τ12 antar dua sel dihitung menggunakan persamaan (22).
o (Errr) o (N2)
(22)
Tabel 1. Error dan konvergensi antara solusi numerik dan solusi reference pada topografi tidak datar (z = 0).
|
Nx |
E rrorRusanov |
ErrorHLLE |
τRusanov |
τHLLE |
|
100 |
0.161517982 |
0.157520289 |
- |
- |
|
200 |
0.075664113 |
0.078228159 |
1.094013686 |
1.009777739 |
|
400 |
0.047301863 |
0.045362923 |
0.677712194 |
0.786174404 |
|
800 |
0.024256513 |
0.019367743 |
0.963524815 |
1.22785781 |
|
1600 |
0.011425722 |
0.007677328 |
1.086086879 |
1.334979601 |
-
3.2 Topografi Datar
Hasil simulasi dengan kasus topografi datar dapat dilihat pada Gambar 9 sampai 13. Pada Gambar 9 dan Gambar 10 dapat dilihat bahwa fluks Rusanov dan fluks HLLE yang diterapkan masih cukup jauh dari fluks reference. Namun fluks yang paling mendekati tetaplah fluks HLLE. Pada Gambar 11 dan 12 gelombang yang dihasilkan fluks Rusanov dan HLLE sudah lebih mendekati fluks reference. Sedangkan pada Gambar 13 fluks reference hampir didekati secara sempurna meskipun masih terlihat perbedaan di beberapa lekukan gelombang. Sama dengan evaluasi bagian sebelumnya (topografi tidak datar) perbedaan ini dikarenakan pembagian sel (Nx) yang berbeda setiap hasil simulasi.
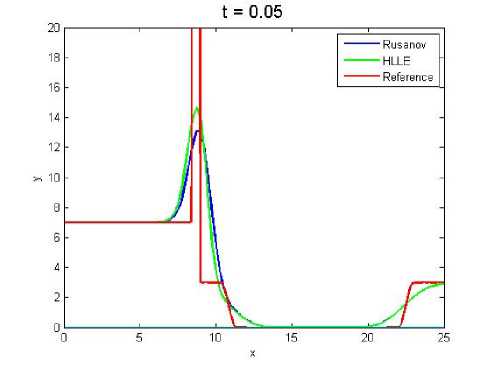
Gambar 9. (Nx= 100)
Untuk melihat konvergensi dan error se-
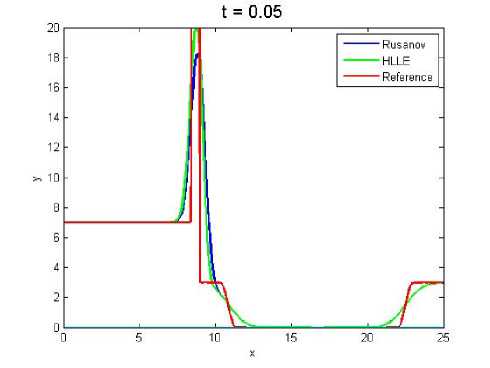
Gambar 10. (Nx = 200)
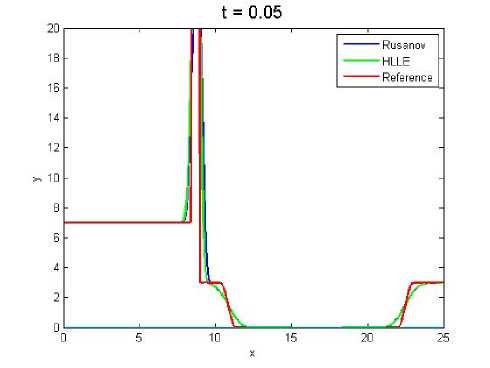
Gambar 11. (Nx = 400)
cara numerik antara kedua fluks dapat dilihat pada Tabel 2. Pada saat Nx = 100 dan Nx = 200 fluks HLLE memiliki error yang lebih besar dibandingkan dengan fluks Rusa-
Tabel 2. Error dan konvergensi antara solusi numerik dan solusi reference pada topografi datar (z = 0).
|
Nx |
E rrorRusanov |
ErrorHLLE |
τRusanov |
τHLLE |
|
100 |
4.163281568 |
4.176158969 |
- |
- |
|
200 |
2.099454075 |
2.153918915 |
0.987706903 |
0.95521269 |
|
400 |
1.138772752 |
1.035167268 |
0.882534352 |
1.057100034 |
|
800 |
0.556136387 |
0.40805968 |
1.03396924 |
1.343011836 |
|
1600 |
0.204869372 |
0.074737235 |
1.440734417 |
2.448881075 |
nov, namun pada Nx selanjutnya fluks HLLE
memiliki error yang lebih kecil. Seperti hal-
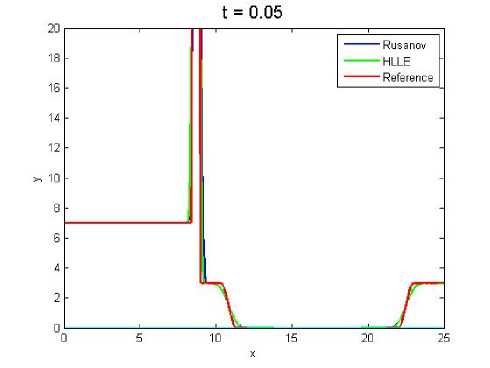
Gambar 12. (Nx = 800)
nya pada kasus topografi tidak datar, simulasi dengan pembagian sel yang lebih sedikit memiliki error yang lebih besar daripada simulasi dengan pembagian sel yang lebih banyak. Rata-rata error yang diperoleh dari hasil simulasi untuk fluks HLLE adalah 1.5696 dan fluks Rusanov adalah 1.6325. Sedangkan konvergensi masing-masing fluks dapat dilihat pada Tabel 2. Cara untuk mendapatkan error dan konvergensi telah dijelaskan pada bagian sebelumnya.
-
4 KESIMPULAN DAN SARAN
t = 0.05
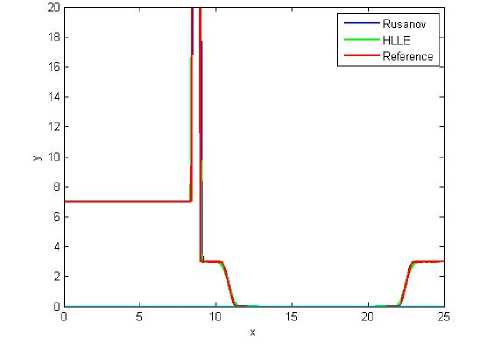
Gambar 13. (Nx= 1600)
Uji numerik yang dilakukan telah menunjukkan ketahanan dari solusi numerik yang telah dipaparkan. Konvergensi yang didapat untuk setiap fluks cenderung menuju ke satu dengan rata-rata konvergensi untuk fluks Rusanov adalah 0.8689 dan fluks HLLE dengan rata-rata konvergensi 1.13810 pada topografi datar. Sedangkan pada topografi tidak datar, rata-rata konvergensi untuk fluks Rusanov adalah 0.76426 dan fluks HLLE dengan rata-rata konvergensi 0.87175. Konvergensi akan bernilai tetap menuju ke satu jika pada waktu setelahnya gelombang berhenti. Sebaliknya, jika gelombang masih bergerak pada waktu selanjutnya maka nilai konvergensi juga akan berubah.
Simulasi yang dihasilkan menunjukkan bahwa fluks HLLE lebih mendekati fluks reference dengan rata-rata error yang lebih kecil dibanding fluks Rusanov. Dimana pada kondisi topografi tidak datar, rata-rata error yang dihasilkan fluks HLLE adalah 0.06403 dan fluks Rusanov dengan rata-rata error 0.06163 pada waktu t = 0.05. Begitu juga dengan kon-
disi topografi datar fluks HLLE memiliki rata-rata galat 1.56960 dan fluks Rusanov memiliki rata-rata error 1.63250 (t = 0.05). Perbedaan error yang dihasilkan dari setiap simulasi dipengaruhi oleh pembagian sel (Nx) yang dilakukan, dimana simulasi dengan Nx yang lebih sedikit akan memiliki galat yang lebih besar dibanding dengan Nx yang lebih banyak.
Daftar Pustaka
Audusse, E., Bouchut, F., Bristeau, M.-O., Klein, R., and Perthame, B. t. (2004). A fast and stable well-balanced scheme with hydrostatic reconstruction for shallow water flows. SIAM Journal on Scientific Computing, 25(6):2050–2065.
Audusse, E., Bristeau, M.-O., and Perthame, B. (2000). Kinetic schemes for SaintVenant equations with source terms on unstructured grids. PhD thesis, INRIA.
Bassi, F. and Rebay, S. (1997). High-order accurate discontinuous finite element solution of the 2d euler equations. Journal of computational physics, 138(2):251–285.
Bon, C. (1997). Mode´lisation et simulation nume´rique d’e´coulements hydrauliques et de ruissellement en topographie quelco-nque. PhD thesis, Bordeaux 1.
Botta, N., Klein, R., Langenberg, S., and Lu¨ tzenkirchen, S. (2004). Well balanced finite volume methods for nearly hydrostatic flows. Journal of Computational Physics, 196(2):539–565.
Bouchut, F. (2004). Nonlinear stability of finite Volume Methods for hyperbolic conservation laws: And Well-Balanced schemes for sources. Springer Science & Business Media.
Chinnayya, A. and LeRoux, A. (1999). A new general riemann solver for the shallowwater equations with friction and topography, 1999. Available in the conservation law preprint server http://www. math. ntnu. no/conservation.
Doyen, D. and Gunawan, P. H. (2014). An explicit staggered finite volume scheme for the shallow water equations. In Finite Volumes for Complex Applications VII-Methods and Theoretical Aspects, pages 227–235. Springer.
Galloue¨t, T., He´rard, J.-M., and Seguin, N. (2003). Some approximate godunov schemes to compute shallow-water equations with topography. Computers & Fluids, 32(4):479–513.
Goutal, N. and Maurel, F. (1997). Proceedings of the 2nd workshop on dam-break wave simulation. Electricite´ de France. Direction des e´tudes et recherches.
Hu, P., Cao, Z., and Pender, G. (2012). Well-balanced two-dimensional coupled modelling of submarine turbidity currents. In Proceedings of the Institution of Civil Engineers-Maritime Engineering, volume 165, pages 169–188. Thomas Telford Ltd.
Klein, R., Botta, N., and Owinoh, A. (2001). Distinguished limits, multiple scales asymptotics, and numerics for atmospheric flows.
LeRoux, A. (1998). Discre´tisation des termes sources raides dans les problemes hyper-boliques. Systemes hyperboliques: noveau schemas et nouvelles applications. Ecoles CEA-EDFINRIA “problemes non line´aires applique´s”, INRIA Rocquencourt (France).
Mungkasi, S. (2011). Metode volume hingga untuk menyelesaikan masalah bendungan-bobol. Jurnal Mat Stat, 11(01).
Quirk, J. J. (1997). A contribution to the great riemann solver debate. In Upwind and High-Resolution Schemes, pages 550–569. Springer.
101
Discussion and feedback