SIMULASI PERGERAKAN RUNTUHAN LONGSOR MENGGUNAKAN MODEL SAVAGE-HUTTER DENGAN FINITE VOLUME METHOD
on
E-Jurnal Matematika, Vol. 7 (2), Mei 2018, pp.88-93
DOI: https://doi.org/10.24843/MTK.2018.v07.i02.p189
ISSN: 2303-1751
SIMULASI PERGERAKAN RUNTUHAN LONGSOR MENGGUNAKAN MODEL SAVAGE-HUTTER DENGAN FINITE VOLUME METHOD
Alifanda Pinkan Ludica1,*, P. H. Gunawan2, Aniq A. Rohmawati3
1Prodi Ilmu Komputasi, Fakultas Informatika – Universitas Telkom [Email:
alifandapl@students.telkomuniversity.ac.id]
2Prodi Ilmu Komputasi, Fakultas Informatika – Universitas Telkom [Email: phgunawan@telkomuniversity.ac.id] 3Prodi Ilmu Komputasi, Fakultas Informatika – Universitas Telkom [Email: aniqatiqi@telkomuniversity.ac.id] ∗ Corresponding Author
Ringkasan
The avalanche is simulated using the Savage-Hutter model with Finite Volume Method (FVM) as a numerical solution in one dimension. The scheme used in FVM is collocated-grid. The aim of this research is to observe the avalanche based on different sediment types on the incline bed with the same initial sediment height. These simulations produce the value of velocity and height avalanche. For each type of sediment has a difference in velocity and height of avalanche affected by the internal angle of friction and the bed friction angle. Sediments with the highest bed friction angle have highest speed. The average velocity of each sediment are Quartz with u = 10.627, Yellow Sand with u = 7.437, and Rice with u = 2.1178 at time t = 1.
Keywords: savage-hutter model, finite volume method, collocated grid, sediment
-
1 PENDAHULUAN
Bencana tanah longsor di Indonesia umumnya terjadi pada musim penghujan. Hujan memicu tanah longsor melalui penambahan beban lereng dan penurunan kuat geser tanah (Soenarmo et al., 2008). Daerah yang terkena longsor mengalami kerugian cukup besar dan menyebabkan korban jiwa. Ada berbagai faktor yang menyebabkan longsor seperti pergeseran lempeng bumi, hujan yang sangat lebat dan lama, struktur tanah yang kurang padat, dan faktor lainnya. Untuk mengetahui pergerakan dari runtuhan longsor dapat disimulasikan dengan persamaan-persamaan matematika. Bentuk dari tanah atau lahan juga berpengaruh penting terhadap kecepatan longsor. Hasil dari simulasi dapat digunakan untuk memprediksi pergerakan dan kecepatan longsor, sehingga bencana longsor yang akan datang dapat diantisipasi.
Pergerakan runtuhan longsor pada penelitian ini disimulasikan menggunakan model Savage-Hutter dengan Finite Volume Method dan skema collocated grid sebagai solusi numerik (Gunawan, 2015). Batasan-batasan yang digunakan antara lain, topografi digambarkan dengan besar sudut yang dibentuk, batas kanan dan kiri menggunakan dirichlet boundary condition, tinggi dan kecepatan awal dari longsor diatur sama, jenis dari sedimen bergantung pada sudut internal tanah dan sudut geser tanah, dan mengabaikan gesekan antara sedimen dengan topografi. Sedimen digambarkan dari ketinggian sedimen dari topografi bukan dari volume sedimen.
Model Savage-Hutter (Pudasaini and Hutter, 2007; Tai et al., 2002) yang disebut juga sebagai model SH, adalah model untuk benda yang menyerupai fluida dinamis yang terdiri dari persamaan diferensial parsial hiper-
bolik yang berdistribusi dari ketinggian dan kecepatan rata-rata komponen di dalam sebuah massa longgar dari butiran tanpa kohesi seperti tanah, biji-bijian, bebatuan dan salju (Hutter et al., 2005). Model ini dirancang untuk memprediksi gerak dan deformasi dari inisial awal agar berjalan di sepanjang trek longsor sesuai dengan topografi yang ditentukan. FVM cukup menarik digunakan pada model permasalahan ini, dimana fluks berperan penting pada simulasi yang dilakukan.
-
2 METODE PENELITIAN
Kx dapat dihitung dengan rumus berikut:
t' - J Kxact, ∂ U/∂X > 0
Kx "| Kxpas, ∂U/∂X < 0 (5)
dengan,
Kxact/xpas = 2sec2(φ) {1 T √1 - Cos2(φ) seC2(δ) } - 1 (6)
dimana φ merupakan sudut internal tanah. Untuk nilai φ dan δ akan dijelaskan lebih detil pada topografi dan sedimen awal.
2.1 Model Savage Hutter
-
2.2 Topografi dan Sedimen Awal
Persamaan pengatur untuk simulasi longsor yang digunakan yaitu model Savage-Hutter. Pada (Pudasaini and Hutter, 2007; Tai
et al., 2002), persamaan Savage-Hutter dalam
bentuk konservatif dapat ditulis sebagai beri-
kut:
∂ h ∂(hu)
∂t ∂x
(1)
∂(hu) ∂(hu2 + 2 β h2) _
∂ t + ∂ x = hSx (2)
Terdapat dua persamaan yaitu, persamaan untuk fluks (1) dan persamaan untuk momentum (2) dengan x merepresentasikan koordinat ruang satu dimensi, t merepresentasikan waktu, u = u (x, t) merupakan kecepatan longsor, h = h (x, t) merupakan tinggi longsor, dan Sx adalah percepatan longsor pada persamaan momentum. SX dan β dapat diperoleh dengan menggunakan persamaan di bawah ini:
Sx = sin(Z) - u tan(δ)cos(Z) (3) Iu I
β = ε Kx cos(Z) (4)
dengan ε = H/L < 1 merupakan rasio dari longsor dimana H merupakan ketebalan longsor dan L adalah panjang longsor, ζ adalah sudut yang dibentuk dari permukaan miring topografi, Kx adalah koefisien tekanan bumi pada sumbu x (Drucker and Prager, 1952), dan δ adalah sudut geser tanah. Sedangkan
Topografi digambarkan berdasarkan sudut kemiringan ζ (x) yang dibentuk seperti pada Gambar 1. Topografi ini bergantung pada ruang x dengan detail sudut kemiringan seperti pada persamaan (7). Diberikan ketinggian awal yang sama untuk setiap sedimen dengan nilai pada persamaan (9).
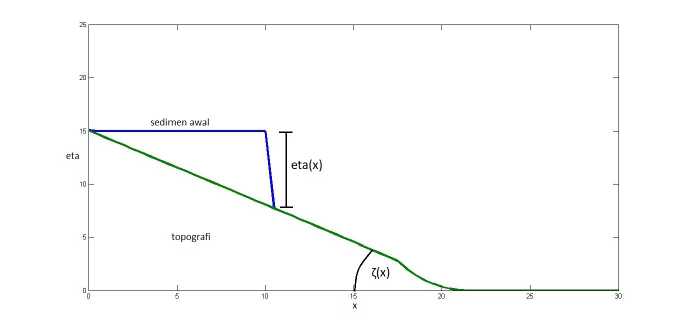
Gambar 1. Inisial awal untuk Topografi dan sedimen.
Zo, 0 ≤ x ≤ 17
ζ(x)= Zo(1 - (x - 17)/4), 17 < x < 21.5 (7)
0, x ≥ 21.5
z(x) = tan(Z (x))(21.5 - x) (8)
dengan sudut kemiringan awal Zo = 35o, kemudian topografi terbentuk dari persamaan (8). Ketinggian sedimen awal dari topografi η (x) dapat dilihat pada persamaan di bawah ini:
η(v) = ∫ max(15,z(x)), x ≤ 10 (9)
^ [ max(0,z(x)), lainnya
Un+1 = Uk - δ (Fk+1 - Fk-1)+p (h) (14) ∆x 2 2
Tabel 1. Jenis-jenis sedimen bergantung pada sudut internal tanah dan sudut geser tanah.
|
No |
Jenis Sedimen |
φ (◦) |
δ (o) |
|
1 |
Yellow Sand |
30 |
21 |
|
2 |
Rice |
40 |
22 |
|
3 |
Quartz |
39 |
27 |
Untuk jenis sedimen yang digunakan, bergantung pada sudut internal tanah φ dan sudut geser tanah δ yang dikutip pada buku (Puda-saini and Hutter, 2007). Nilai dari φ dan δ tertulis pada Tabel 1. Pada umumnya semakin padat suatu tanah akan didapatkan nilai sudut internal tanah yang semakin besar pula (Sumiyanto et al., 2005).
-
2.3 Model Numerik
Pada penelitian ini, untuk mendekati solusi analitik dari model Savage-Hutter digunakan Finite Volume Method dengan skema collocated-grid sebagai solusi numerik pada satu dimensi (Gunawan, 2015). Dalam solusi numerik ini terdapat diskritisasi ruang dan waktu yang dilakukan pada domain Ω(0, L). Persamaan (1) sampai (2) diubah ke dalam bentuk matriks menjadi:
U=[ h ] (10)
F = [ hu2 +Uβ h2 ] (11)
S = [ hSx ] (12) sehingga persamaan (1)-(2) dapat ditulis ulang sebagai:
∂U ∂ F (U)
∂ t + ∂ x
(13)
kemudian dilakukan diskritisasi ruang dan waktu pada persamaan (13), sehingga:
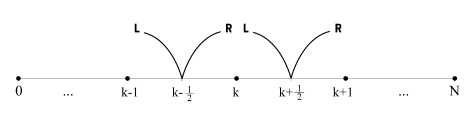
Gambar 2. Diskritisasi pada domain Ω(0, L) menjadi sejumlah N bagian.
dengan ∆t adalah langkah waktu, ∆x adalah langkah spasial, k adalah indeks untuk node spasial, dan n adalah indeks untuk langkah waktu. Dari Gambar 2, ruang didiskri-tisasi menjadi N bagian sehingga didapatkan ∆x = L/N, dimana L adalah panjang dari ruang. Untuk mencari nilai Ukn+1 dibutuhkan nilai F pada node k ± 1/2.
Fk± 2 =t 1F (U)R +12F (U)L
- 13 (UR - UL) + P(hk) - P(hm)
(15)
Dimana R adalah nilai pada bagian kanan dari k ± 1/2, dan L adalah nilai pada bagian kiri dari k ± 1/2. Penempatan k ± 1/2 terletak seperti Gambar 2. Untuk nilai 11,12,13 dan p (h) dapat dihitung dengan persamaan berikut:
|
min(c2,0) - |
- min( c 1,0) |
(16) |
|
t1 = c2 - |
c1 | |
|
t2 = 1 - |
t1 |
(17) |
|
. _ c21c 11- |
- c 11 c 21 |
(18) |
|
3 2(c2 - |
- c 1) |
PCh) = 2 gh2 (19)
dengan c merupakan kecepatan gelombang (Mungkasi and Roberts, 2012). Persamaan kecepatan gelombang didefinisikan seperti berikut:
uR-2 ghRm,
I min( Ul - Vghm, u * - √gh*),
c 2={
Ul + 2 Vhhm, max( Ur + Vghm, u * + √gh*),
hm = 0
hm > 0
(20)
hm = 0
hm > 0
(21)
dimana hm merupakan ketinggian longsor modifikasi dengan topografi ∆z, dengan nilai ∆z = zk +1 — zk. Modifikasi dari h dan ∆z ini dinamakan reconstruction scheme yang sudah dijelaskan pada (Audusse et al., 2004; Bouchut, 2004). Sedangkan u∗ dan h∗ merupakan kecepatan dan ketinggian longsor setelah dimodifikasi menggunakan hm . Kecepatan u∗ dan ketinggian h∗ longsor inilah yang digunakan dalam persamaan numerik (14).
u * = 2 ( ul+ur )+Vghm—Vghm (24)
g
-
3 HASIL DAN PEMBAHASAN
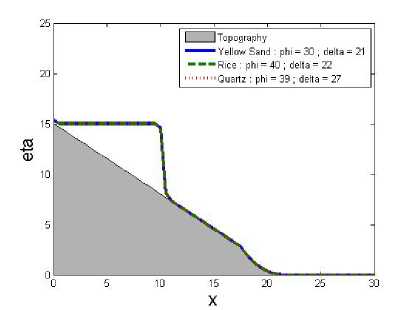
Gambar 3.
Pada penelitian ini simulasi yang dilakukan akan menghasilkan pergerakan longsor seperti pada Gambar 3 sampai Gambar 8.
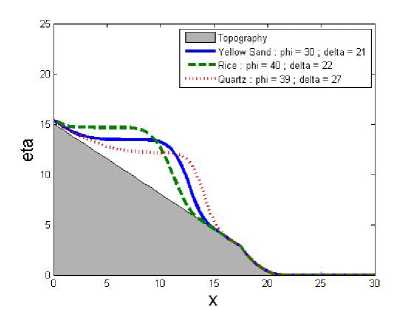
Gambar 4.
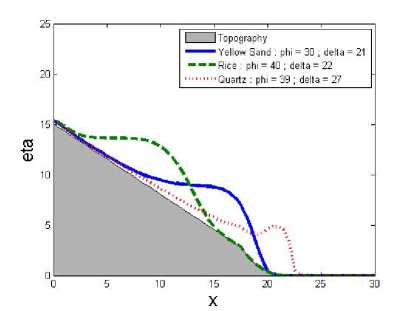
Gambar 5.
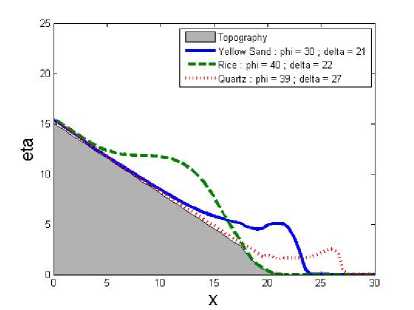
Gambar 6.
Sedimen dengan garis solid (—) adalah Yellow Sand dengan φ = 30; δ = 21, sedimen dengan garis patah-patah (- - -) adalah Rice dengan φ = 40; δ = 22, dan sedimen dengan garis titik-titik (...) adalah Quartz dengan φ = 39; δ = 27. Gambar 3 pada waktu t = 0.005 menunjukkan kondisi awal dari longsor, dengan ketinggian awal setiap sedimen bernilai sama yaitu h = 15 pada x ≤ 10. Kemudian pada Gambar 4 dengan waktu t = 0.5, pergera-
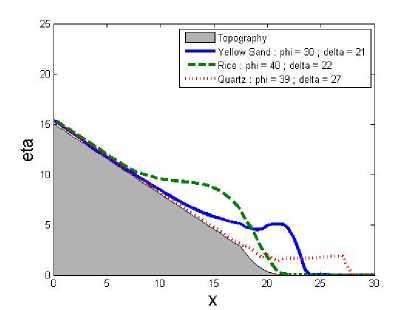
Gambar 7.
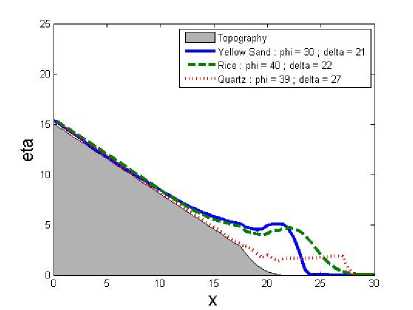
Gambar 8.
kan setiap longsor mulai menunjukkan perbedaan kecepatan. Pada Gambar 5 dengan waktu t = 1, karena sedimen Quartz memiliki kecepatan paling tinggi maka sedimen Quartz sudah berada pada bidang datar. Pada Gambar 6 dengan waktu t = 1.5, sedimen Yellow Sand sudah berada pada bidang datar. Pada Gambar 7 dengan waktu t = 2.005, sedimen Quartz dan Yellow Sand sudah berhenti karena tidak ada percepatan longsor lagi, dan sedimen Rice masih berjalan karena masih berada pada bidang miring. Dan pada Gambar 8 dengan waktu t = 3.005, sedimen Rice sudah berhenti karena percepatan longsor yang mengecil.
Dapat dilihat bahwa sedimen Quartz memiliki kecepatan longsor tertinggi dan Rice memiliki kecepatan terendah. sudut geser tanah δ yang tinggi akan menyebabkan kecepatan longsor menjadi tinggi, dan sebaliknya. Sudut internal tanah φ juga mempengaruhi kecepatan longsor, jika nilai dari φ semakin
tinggi, maka kecepatan longsor akan rendah. Jika nilai φ tinggi dan δ tinggi, yang berpengaruh besar pada kecepatan longsor adalah δ, sehingga kecepatan longsor akan tinggi meskipun memiliki nilai φ yang besar, tetapi tidak secepat kecepatan sedimen dengan φ yang lebih rendah. Kecepatan rata-rata setiap sedimen adalah Quartz dengan u = 10.627, Yellow Sand dengan u = 7.437, dan Rice dengan u = 2.1178 pada waktu t = 1.
-
4 KESIMPULAN DAN SARAN
Pada simulasi yang telah dilakukan dapat disimpulkan bahwa, semakin tinggi nilai sudut geser tanah δ maka kecepatan longsor akan tinggi juga, begitu sebaliknya. Jika nilai sudut internal tanah φ besar maka kecepatan akan mengecil. Tetapi δ lebih berpengaruh terharap kecepatan longsor, sehingga jika nilai δ dan φ tinggi maka kecepatan longsor tetap tinggi meskipun lebih rendah dari sedimen yang memiliki nilai φ yang rendah. Kecepatan rata-rata setiap sedimen adalah Quartz dengan u = 10.627, Yellow Sand dengan u = 7.437, dan Rice dengan u = 2.1178 pada waktu t = 1.
Pustaka
Audusse, E., Bouchut, F., Bristeau, M.-O., Klein, R., and Perthame, B. t. (2004). A fast and stable well-balanced scheme with hydrostatic reconstruction for shallow water flows. SIAM Journal on Scientific Computing, 25(6):2050–2065.
Bouchut, F. (2004). Nonlinear stability of finite Volume Methods for hyperbolic conservation laws: And Well-Balanced schemes for sources. Springer Science & Business Media.
Drucker, D. C. and Prager, W. (1952). Soil mechanics and plastic analysis or limit design. Quarterly of applied mathematics, 10(2):157–165.
Gunawan, P. H. (2015). Numerical simulation of shallow water equations and related models. PhD thesis, Universite´ Paris-Est.
Hutter, K., Wang, Y., and Pudasaini, S. P. (2005). The savage–hutter avalanche model: how far can it be pushed? Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 363(1832):1507– 1528.
Mungkasi, S. and Roberts, S. G. (2012). Analytical solutions involving shock waves for testing debris avalanche numerical models. Pure and applied geophysics, 169(10):1847–1858.
Pudasaini, S. P. and Hutter, K. (2007). Avalanche dynamics: dynamics of rapid flows of dense granular avalanches. Springer Science & Business Media.
Soenarmo, S. H., Sadisun, I., and Saptoharto-no, E. (2008). Kajian awal pengaruh intensitas curah hujan terhadap pendugaan potensi tanah longsor berbasis spasial di kabupaten bandung, jawa barat. Jurnal Geo-aplika, 3(3):133–141.
Sumiyanto, S., Pamudji, G., and Susanto, H. A. (2005). Prediksi sudut gesek internal tanah berdasarkan sudut dilatasi pada uji geser langsung. Dinamika Rekayasa, 1(1):16–20.
Tai, Y.-C., Noelle, S., Gray, J., and Hutter, K. (2002). Shock-capturing and front-tracking methods for granular avalanches. Journal of Computational Physics, 175(1):269– 301.
93
Discussion and feedback