LAJU PERTUMBUHAN BAKTERI S. Aerous MELALUI PENDEKATAN PERSAMAAN DIFERENSIAL
on
E-Jurnal Matematika Vol. 6 (3), Agustus 2017, pp. 183-187
DOI: https://doi.org/10.24843/MTK.2017.v06.i03.p164
ISSN: 2303-1751
LAJU PERTUMBUHAN BAKTERI S. Aerous MELALUI PENDEKATAN PERSAMAAN DIFERENSIAL
Nurdeni1§, Witri Lestari2, dan Seruni3
1Program Studi Pendidikan Matematika, FTMIPA, Universitas Indraprasta PGRI [Email: nurdeni@unindra.ac.id]
2Program Studi Pendidikan Matematika, FTMIPA, Universitas Indraprasta PGRI [Email: witrilestari.unindra@gmail.com]
3Program Studi Pendidikan Matematika, FTMIPA, Universitas Indraprasta PGRI [Email : taso8060@gmail.com]
§Corresponding Author
ABSTRAK
Penelitian ini bertujuan untuk membuat model laju pertumbuhan bakteri S. Aerous melalui pendekatan persamaan diferensial. Jenis penelitian ini adalah riset dan pengembangan (Research and Deveopment). Penelitian model riset dan pengembangan merupakan penelitian yang bertujuan untuk memperoleh suatu sistem pengembangan pengetahuan di suatu tempat yang kemudian divalidasi dan dikembangkan untuk diterapkan pada tempat-tempat yang lain. Subjek penelitian ini adalah bakteri S. Aureus, teknik pengumpulan data yang digunakan dalam penelitian ini adalah proses laboratorium dimana melihat pertumbuhan laju bakteri tersebut. Adapun teknik analisis datanya adalah dengan pendekatan model persamaan diferensial. Berdasarkan hasil pengamatan, hasil uji laju pertumbuhan bakteri S. Aerous di laboratorium terlihat jelas bahwa laju perkembangan atau pertumbuhannya meningkat, hal ini menunjukkan bahwa bakteri khususnya bakteri S. Aerous ini mempunyai pertumbuhan yang sangat pesat. Hal ini dibuktikan dengan beberapa model persaman pertumbuhan bakteri yaitu : Populasi bakteri pada setiap waktu adalah :
N (t) =
1,3
1 + 11,589e-0-3 8 7 t
Kata Kunci: Laju pertumbuhan, Bakteri S.Aureus, persamaan differensial
-
1. PENDAHULUAN
Berkaitan dengan gejala atau fenomena alam, orang sering memerlukan model matematik dari masalah yang dihadapi. Banyak permasalahan matematik dari gejala alam yang model matematikanya dapat diformulasikan dalam bentuk persamaan diferensial orde-1. Selanjutnya dari model matematik yang diperoleh ini solusinya dicari dengan metode yang sesuai. Pemodelan matematika ini digunakan untuk merepresentasikan dan menjelaskan sistem-sistem fisik atau problem dalam dunia nyata dan dalam pernyataan matematika, sehingga diperoleh pemahaman dari problem dunia real ini menjadi lebih tepat (Widowati dan Sutimin, 2007: 1).
Aplikasi matematika dapat diterapkan dalam banyak disiplin ilmu seperti fisika, ilmu biologi dan kedokteran, teknik, ilmu sosial dan politik, ekonomi, bisnis dan keuangan, juga problem-problem jaringan komputer. Disiplin ilmu yang akan diterapkan adalah ilmu biologi dan matematika khususnya mikrobiologi yang akan berhubungan dengan persamaan diferensial.
Secara umum langkah-langkah untuk menyelesaikan masalah persamaan diferensial adalah : (1) Membentuk model matematis dari permasalahan, (2) Menentukan solusi umum, (3) Menggunakan kondisi awal untuk menentukan solusi khusus, (4) Menggunakan informasi selanjutnya, dan (5) Pemeriksaan
hasil yang diperoleh, dimana dengan pola perkembangan ilmu matematika kita bisa menduga model persamaan diferensial yang tepat untuk perkembangan mikroorganisme sesuai dengan data histori yang berisi data pertumbuhan terhadap waktu. Setiap organisme yang mengalami pertumbuhan ditandai dengan penambahan jumlah sel atau pembesaran ukuran sel dari organisme tersebut. Penambahan jumlah sel atau pembesaran ukuran sel tersebut dapat dilihat dari data pertumbuhan setiap organisme. Terkait dengan pertumbuhan organisme, banyak hal yang mempengaruhi laju pertumbuhan dari setiap organisme (Hasan, 2001:3).
Persamaan diferensial dapat berhubungan dengan mikrobiologi sebagai disiplin ilmu biologi dan matematika. Salah satu contoh persamaan diferensial yang berhubungan dengan mikrobiologi adalah perkembangan bakteri, misalnya bakteri S. Aureus yang merupakan salah satu bakteri yang dapat merusak kekebalan tubuh manusia. Banyak model matematika telah dikembangkan untuk tujuan memprediksi pertumbuhan bakteri (Teleken, et al., 2011).
Penelitian ini akan dilakukan untuk mengaplikasikan model pengukuran persamaan diferensial terhadap laju perkembangan bakteri S. Aureus. Persamaan diferensial sering muncul dalam model matemtika yang mencoba menggambarkan keadaan kehidupan nyata. Banyak hukum-hukum alam dan hipotesa-hipotesa dapat diterjemahkan kedalam persamaan yang mengandung turunan melalui bahasa matematika. Dalam kehidupan sehari-hari, banyak fenomena yang dalam menyelesaikannya menggunakan persamaan diferensial orde satu.
-
2. DATA DAN METODE
Data yang diperoleh adalah hasil pengukuran bakteri S. Aureus di laboratorium dengan menggunakan UV.
Jenis penelitian ini adalah riset dan pengembangan (Research and Development). Penelitian model riset dan pengembangan
merupakan penelitian yang bertujuan untuk memperoleh suatu sistem pengembangan pengetahuan di suatu tempat yang kemudian divalidasi dan dikembangkan untuk diterapkan pada tempat-tempat yang lain.
Penelitian ini dirancang untuk dua tahap. Pada tahap pertama menguji coba model pengukuran laju perkembangan bakteri melalui konsep persamaan diferensial dan tahap kedua mengaplikasikan model pengukuran laju perkembangan bakteri melalui konsep persamaan diferensial.
Subjek penelitian ini adalah bakteri S. Aureus, teknik pengumpulan data yang digunakan dalam penelitian ini adalah proses lab dimana melihat perkembangan laju bakteri tersebut. Adapun teknik analisis datanya adalah memakai salah satu model Persamaan Differensial.
-
3. HASIL DAN PEMBAHASAN
Berdasarkan hasil penelitian hubungan waktu dengan nilai optical density dinyatakan dalam tabel 1.
Apabila N(t) adalah populasi bakteri pada waktu t, maka laju pertumbuhan populasi bakteri adalah
dN(t)
= R N(t) atau N(t) = R dt N(t)dt
R adalah laju reproduksi, dan umumnya bergantung pada populasi bakteri pada waktu t, jadi R = f(N(t)). Selanjutnya R diasumsikan linier, maka f(N(t)) = a – bN(t) yang berarti untuk media yang terbatas maka laju reproduksi
adalah 0 dan terjadi ketika N = .
Laju populasi dengan laju reproduksi f(N(t))
dN(t)
adalah = ( a – bN(t))N(t)
dt
(1)
Tabel 1. Hubungan Waktu dengan Nilai Optical Density
|
Waktu |
Nilai Optical Density | ||
|
Tabung 1 |
Tabung 2 |
Nilai Tengah | |
|
0 |
0,099 |
0,097 |
0,098 |
|
1 |
0,172 |
0,173 |
0,1725 |
|
2 |
0,267 |
0,267 |
0,267 |
|
3 |
0,368 |
0,362 |
0,365 |
|
4 |
0,44 |
0,438 |
0,439 |
|
5 |
0,531 |
0,531 |
0,531 |
|
6 |
0,696 |
0,697 |
0,6965 |
|
7 |
0,729 |
0,73 |
0,7295 |
|
8 |
0,83 |
0,833 |
0,8315 |
|
9 |
0,896 |
0,898 |
0,897 |
|
10 |
0,91 |
0,91 |
0,91 |
|
11 |
0,994 |
0,99 |
0,992 |
|
12 |
1,162 |
1,163 |
1,1625 |
|
13 |
1,199 |
1,197 |
1,198 |
|
14 |
1,092 |
1,092 |
1,092 |
|
15 |
1,182 |
1,179 |
1,1805 |
|
16 |
1,201 |
1,207 |
1,204 |
|
17 |
1,284 |
1,285 |
1,2845 |
|
18 |
1,288 |
1,288 |
1,288 |
|
19 |
1,299 |
1,296 |
1,2975 |
|
20 |
1,299 |
1,3001 |
1,29955 |
|
21 |
1,299 |
1,299 |
1,299 |
|
22 |
1,298 |
1,298 |
1,298 |
|
23 |
1,297 |
1,296 |
1,2965 |
|
24 |
1,297 |
1,297 |
1,297 |
|
25 |
1,297 |
1,297 |
1,297 |
Persamaan 1 adalah persamaan diferensial orde 1 yang dinamakan persamaan logistic dari
dN(t) persamaan 1 apabila
0, laju
pertumbuhan disebut dalam keadaan seimbang, dN(t)
Sehingga jika = 0, maka N = 0 atau N =
dt
a
. Solusi persamaan diferensial 1 didapat
dengan metode pemisahan perubah sebagai berikut:
dN(t)
(a - bN(t))N(t)
dt
(2)
Integralkan kedua didapat
dN(t)
∫ (a - bN(t))N(t)
ruas persamaan 2,
=∫dt
— ln∣N∣ - — ln∣a - bN∣ = t + c aa
dengan syarat awal N(0) = No didapat c =
— ln∣No∣ - — ln∣a - bNol sehingga solusi aa
persamaan diferensial dengan syarat awal
adalah
N
No
a - bNo a - bN
= eat
⇔ N(t) = —
1 +
a
b
a - bNo Λ
—----Ie
bNo j
(3)
-at
a
populasi maksimal bakteri dalam media,
berdasarkan data hasil pengamatan pada tabel 1
a
= 1, 299 ~ 1,3 b, ,
Selajutnya untuk menaksir parameter a, dan b berdasarkan data hasil pengamatan, Terlebih dahulu mengubah bentuk persamaan 3.
• n i a - bNo misalkan k = , sehingga
bNo
persamaan 3 menjadi
1 3
⇔ N(t) =--
1 + ke-at
⇔ N(t) + N(t)ke-at = 1,3
⇔ N(t)ke-at = 1,3 - N(t)
logaritma kedua ruas persamaan terakhir
⇔ ln N(t)ke
-at
= ln1,3 - N(t)∣
⇔ ln∣k∣ - at = ln
1,3 — N(t)
N(t)
metode kuadrat terkecil maka parameter a dan ln k
dengan membuat pasangan data
dan waktu jam t , serta
Tabel 2. Perhitungan Parameter a, dan ln (k)
dimana:
ln∣k∣ = 2,45 → k = 11,589
-a = -0,387 → a =0,387
Jadi populasi bakteri pada setiap waktu adalah
N (t) =------ 0≡ (4)
1 +11,589e
Untuk nilai t = 0, 1, 2, .... 25, maka populasi
bakteri berdasarkan solusi persamaan diferensial (persamaan 4), mendekati nilai data hasil pengamatan lihat grafik 2.
Regression Summary for Dependent Variable: OBS (Spreadsh R= ,95881683 R²= ,91932972 Adjusted R²= ,91596846 F(1,24)=273,51 p<,00000 Std.Error of estimate: ,89567
|
N=26 |
Beta |
Std.Err. of Beta |
B |
Std.Err. of B |
t(24) |
p-level |
|
Intercept |
-0,958817 |
0,05797 |
2,45147 -0,387334 |
0,34141 0,023421 |
7,1804 -16,5381 |
0,00000 0,00000 |
|
T |
Gambar 2. Grafik Data Hasil Pengamatan dan Pemodelan Persamaan Diferensial
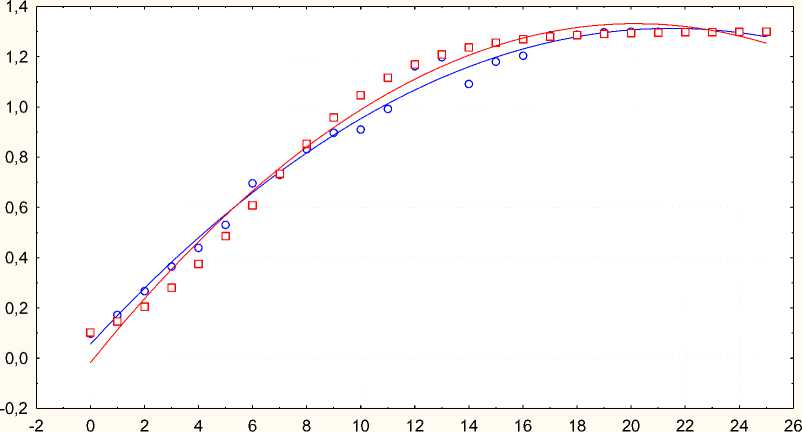
T
Populasi Bakteri Berdasarkan Data Sampel
Populasi Bakteri Berdasarkan Solusi Persamaan diferensial
-
4. SIMPULAN DAN SARAN
Simpulan
Dilihat dari hasil uji bakteri di laboratorium terlihat jelas bahwa laju perkembangan atau pertumbuhannya meningkat, hal ini menunjukkan bahwa bakteri khususnya bakteri S. Aerous ini mempunyai pertumbuhan yang sangat pesat. Jadi populasi bakteri pada setiap waktu adalah :
N (t) =
1,3
1 +11,589e ~0≈3s7
Saran
Lebih dalam lagi dipelajari uji bakteri dilihat dari setiap faktornya yang mempengaruhi pertumbuhan atau
DAFTAR PUSTAKA
Hasan, Oskar, 2001. Studi Tentang Beberapa Model Pertumbuhan.Bogor. Fakultas Matematika dan Ilmu Pengetahuan Alam IPB.
Teleken, T.J., W.S. Robazza, and G. Almeida. 2011. Mathematical modelling of microbial growthin milk. Cience. Technol. Aliment. 31(4):34-41.
Widowati dan Sutimin. 2007. Buku Ajar Pemodelan Matematika. Semarang. FMIPA Diponegoro.
perkembangan laju bakteri khususnya bakteri S.
Aerous dan lebih jauh lagi aplikasikan dengan beberapa solusi yang ada selain menggunakan persamaan diferensial.
187
Discussion and feedback