PENENTUAN CADANGAN PREMI DENGAN METODE PREMIUM SUFFICIENCY PADA ASURANSI JIWA SEUMUR HIDUP JOINT LIFE
on
E-Jurnal Matematika Vol. 5 (3), Agustus 2016, pp. 98-102
ISSN: 2303-1751
PENENTUAN CADANGAN PREMI DENGAN METODE PREMIUM SUFFICIENCY PADA ASURANSI JIWA SEUMUR HIDUP JOINT LIFE
Ni Putu Mirah Permatasari1§, I Nyoman Widana2, Kartika Sari3
1Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: mirahpermataa@gmail.com] 2Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: nwidana@yahoo.com] 3Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: sari_kaartika@yahoo.co.id] §Corresponding Author
ABSTRACT
The aim of this research was to get the formula of premium reserves through the premium sufficiency method. Premium reserve is the amount of fund that is collected by the insurance company in preparation for the claim’s payment. Premium sufficiency method is gross premium calculation. To construct that formula, this research used Tabel Mortalitas Indonesia (TMI) 2011, interest rate 2.5% and cost of alpha 0.05%. Based on simulation result in men premium reserve value of age 1 of 56 years propotional with insured periods, but after56 years enhancement of premium reserve value.
Keywords: Joint Life Insurance, Premium Reserve, Premium Sufficiency
Asuransi jiwa seumur hidup adalah asuransi yang memberikan perlindungan mulai dari awal disepakatinya kontrak sampai meninggal dunia (Sembiring, 1986). Berdasarkan banyaknya tertanggung asuransi jiwa dibedakan menjadi 2, yaitu asuransi jiwa tunggal dan asuransi jiwa kumpulan. Asuransi jiwa Joint Life adalah asuransi jiwa yang menanggung 2 orang pemegang polis atau lebih (Futami [2]).
Salah satu metode perhitungan cadangan premi dengan perhitungan premi kotor adalah metode premium sufficiency. Premi kotor dihitung dengan melibatkan biaya yang diperlukan perusahaan (Futami, 1994).
Pada penelitian sebelumnya siregar (2014), telah melakukan perhitungan cadangan premi asuransi dwiguna joint life status last survivor dengan metode premium sufficienc. Sementara itu, sejauh ini peneliti belum menemukan penelitian mengenai perhitungan cadangan premi dengan metode premium sufficiency pada asuransi jiwa seumur hidup joint life. Oleh karena itu dalam penelitian ini dibahas perhitungan cadangan premi dengan metode
premium sufficiency pada asuransi jiwa seumur hidup joint life.
Selanjutnya dibahas konsep-konsep yang digunakan untuk menentukan formula cadangan premi.
Anuitas hidup adalah suatu anuitas yang pembayarannya dilakukan selama tertanggung masih hidup (Futami, 1993). Nilai sekarang anuitas awal dari anuitas seumur hidup untuk pemegang polis berusia X tahun dengan uang pertanggungan sebesar Rp.1,- dirumuskan sebagai (Futami, 1993):
̈X=1+vpx + V2 2Px+⋯+
^ω X ω-x-ιPx (1)
Persamaan (1) dapat digeneralisasikan untuk merumuskan nilai sekarang anuitas awal dari anuitas seumur hidup joint life pada pemegang polis berusia X tahun dan y tahun dengan uang pertanggungan sebesar Rp.1,- menjadi:
̈ ■xy =1+vpxy + V2 2Pxy+⋯
+ vω x , y ω-x-l,ω-y-lPxy (2)
Karena Pxy = ,y+ι , maka
^xy
^x =
I + v2 ⅛+l—⅛+2 lX lX
+⋯+
persamaan (2) dapat ditulis sebagai:
V
(8)
_ -1 i lχ+ι,y+ι 2 ΩΩ lχ+2,y+2 l
̈ ■xy =1+V ,+V299 , +⋯
ixy ixy
+
yω-x-l,ω-y-l ^⅛>, ^χy
Persamaan (3) dikalikan dengan
(3)
( v≡( )) ∖V2 ( x+y))
Persamaan (8) dapat digeneralisasikan untuk merumuskan premi tunggal asuransi jiwa seumur hidup joint life pada pemegang polis berusia X tahun dan y tahun dengan uang pertanggungan sebesar Rp.1,- diperoleh:
-
diperoleh:
λ iχy - lx+i,y+ι ^xy = ,
■xy
-
a =
ι ,
I X+1,y+ι - tX+ 2 ,y+2 +V --------:----------
V2( x+y ) ιxy
( V2 ( χ+y ) ^χy +
■xy
2 (x+y+2)ι
U LX+1,y+ι
( x+y+4 )
v bX+2,y+2
17ω-x,ω~yl } v tω,)
+
+⋯+
(4)
Selanjutnya karena ^xy = ( χ+y)×^xy , maka
persamaan (4) menjadi:
̈ χy = ( ^xy + ¾+l ,y+ι + ^χ+2 ,y+2 +
⋯+Dω, ω )
(5)
Persamaan
menjadi
A =
=
+⋯+ vω-x-l ,ω-y-l⅛, ^χy
(9)
■ ∙ (( x+y )
(9) dikalikan dengan ( ),
ι
V2( x+y ) ιxy
( V2 ( χ+y ) +1 (^xy
-
12(χ+y) +2 ( Z-V-L-I TJ-L-I
( ,y+ι
-
lχ+2,y+2)+⋯+vω x ,ω y^ω,ω) (10)
Karena ^xy = + Dχ+ι,y+ι + Dχ+2,y+2 +
⋯+ , , maka persamaan (5) menjadi:
.. __ ^xy
̈ χy (6)
uxy
Sedangkan untuk pemegang polis berusia
X+t tahun dan y+t tahun maka persamaan (6)
Karena Cχy = ( χ+y )+ × ^χy , maka
persamaan (10) menjadi:
^xy = ( Cχ ,y+ Cχ+ι,y+ι + Cχ+2,y+2 +
uX,y
⋯+Cω ,ω)
(11)
menjadi:
̈x+t, =
Nχ+t,y+t D x+t,y+t
(7)
Premi adalah sejumlah uang yang wajib dibayarkan oleh tertanggung kepada perusahaan sesuai dengan kontrak yang telah disepakati. Premi yang dibayarkan sekaligus disebut premi tunggal sedangkan premi yang dibayar berkala setiap tahun disebut premi tahunan (Futami, 1993
Perhitungan premi tunggal asuransi jiwa seumur hidup untuk pemegang polis berusia X tahun dinotasikan Ax dan dirumuskan sebagai (Futami, 1993):
Selanjutnya karena ^xy = + , + ^χ+2 ,y+2+⋯+C(ι> ,ω, maka persamaan (11) dapat ditulis sebagai:
A Mxy
^xy = υxy
(12)
Sama halnya dengan nilai anuitas hidup, untuk pemegang polis berusia X+t dan pemegang polis berusia y+t persamaan (12) menjadi:
A _ Mχ+t,y+t
Aχ+t,y+t = ^x+t ,y+t
(13)
Premi tahunan asuransi jiwa seumur hidup untuk pemegang polis berusia X tahun yang
dibayarkan pada awal tahun dinotasikan dengan Pχ dan dirumuskan sebagai
px = ̈J (14)
Persamaan (14) dapat digeneralisasikan untuk merumuskan premi tahunan asuransi jiwa seumur hidup joint life bagi pemegang polis berusia X tahun dan y tahun untuk uang pertanggungan sebesar Rp.1,- dibayarkan di akhir tahun menjadi:
R = xy (15)
∙^∙y
uxy
Selanjutnya, berdasarkan persamaan (6) dan persamaan (12), maka persamaan (15) menjadi:
P Mχy rχy = lNxy
(16)
Pada penelitian ini data yang digunakan adalah data sekunder yang bersumber dari artikel sebagai hasil penelitian siregar (2014).
Langkah yang dilakukan adalah menghitung nilai dari tabel mortalitas joint life berdasarkan Tabel Mortalitas Indonesia (TMI) 2011, selanjutnya menghitung nilai dari tabel komutasi joint life dengan tingkat bunga 2,5 %, lebih lanjut lagi dapat dilakukan perhitungan cadangan premi dengan metode premium sufficiency melalui simulasi dari peserta asuransi jiwa seumur hidup joint life.
Untuk memudahkan perhitungan, dalam penelitian ini digunakan program Software Microsoft Excel
Sebelum memperoleh formula cadangan premi pada asuransi jiwa seumur hidup joint life maka terlebih dahulu ditentukan premi kotor pada asuransi jiwa seumur hidup joint life. Formula Premi Kotor pada Asuransi JIwa Seumur Hidup Joint Life diperoleh:
p- ∗= { pχy ̈ +r } (17)
Karena berlaku persamaan (6) dan persamaan (16) maka persamaan (17) dapat ditulis sebagai:
R∗ = \ { Mxy + θDχy + y } (18)
y (^xy ^xy )
Selanjutnya formula cadangan premi dengan metode Premium Sufficiency pada asuransi jiwa seumur hidup Joint Life diperoleh:
tVxy = ,y+t-(Rχyax+t,y+t +
÷ ) ax+1,y+t (19)
u-xy∕
Karena berlaku persamaan (7), (13) dan (16) maka persamaan (19) menjadi:
tVxy = (Mχ+t,y+t-(Mxy + ^^xy ) ⅛ , Z±£)(22)
ux+1,y+t ∖ nxy /
Terdapat dua orang pemegang polis yang mengikuti asuransi jiwa seumur hidup joint life pada salah satu perusahaan asuransi jiwa. Usia pemegang polis mulai mengikuti asuransi jiwa adalah usia (X)=35 tahun dan (y)=30 tahun. Pembayaran premi dilakukan setiap tahun selama pemegang polis masih hidup. Uang pertanggungan sebesar Rp,10.000.000,-. Asuransi jiwa berakhir jika pemegang polis berusia X tahun atau y tahun meninggal dunia.
Berdasarkan Tabel 4.1 dapat dilihat apabila salah satu dari pemegang polis berusia X=35 dan pemegang polis berusia y=30 tahun meninggal 1 tahun kemudian maka nilai cadangan premi pada asuransi jiwa seumur hidup joint life adalah Rp. 110313.07683 , selanjutnya setelah 2 tahun nilai cadangan preminya adalah Rp. 273801.78611 dan demikian seterusnya.
Selanjutnya, jika dibuat grafik hubungan antara nilai cadangan premi dengan peningkatan tahunya berikut dapat dilihat grafik seperti pada gambar 1.
Tabel 4.1 Nilai Cadangan Premi dengan Metode Premium Sufficiency pada Asuransi Jiwa Seumur Hidup Joint Life untuk pemegang polis berusia % = 35 dan berusia y = 30
|
Jangka Waktu (t) |
tv (Rp) |
Jangka Waktu (t) |
tv (Rp) |
|
1 |
110313.077 |
39 |
6912912.050 |
|
2 |
273801.786 |
40 |
7069925.861 |
|
3 |
440395.614 |
41 |
7223596.827 |
|
4 |
610221.357 |
42 |
7373892.167 |
|
5 |
783041.369 |
43 |
7520010.182 |
|
6 |
958633.930 |
44 |
7661075.859 |
|
7 |
1136439.253 |
45 |
7796204.888 |
|
8 |
1316448.851 |
46 |
7925524.377 |
|
9 |
1498751.755 |
47 |
8048302.702 |
|
10 |
1683030.698 |
48 |
8165640.620 |
|
11 |
1869076.058 |
49 |
8278009.997 |
|
12 |
2056463.750 |
50 |
8385413.361 |
|
13 |
2244726.723 |
51 |
8487491.066 |
|
14 |
2433512.339 |
52 |
8582241.210 |
|
15 |
2622651.547 |
53 |
8669300.067 |
|
16 |
2811643.855 |
54 |
8749207.294 |
|
17 |
2999894.468 |
55 |
8822046.964 |
|
18 |
3186997.953 |
56 |
8887723.504 |
|
19 |
3372994.306 |
57 |
8950377.397 |
|
20 |
3557948.972 |
58 |
9007644.887 |
|
21 |
3741955.145 |
59 |
9059546.376 |
|
22 |
3925073.372 |
60 |
9105350.379 |
|
23 |
4107219.367 |
61 |
9145277.128 |
|
24 |
4288409.864 |
62 |
9187062.764 |
|
25 |
4468813.378 |
63 |
9228862.006 |
|
26 |
4648579.511 |
64 |
9268968.912 |
|
27 |
4827950.663 |
65 |
9305747.216 |
|
28 |
5007109.043 |
66 |
9335079.000 |
|
29 |
5186142.108 |
67 |
9360645.234 |
|
30 |
5364872.609 |
68 |
9379281.401 |
|
31 |
5543029.516 |
69 |
9400886.154 |
|
32 |
5720447.231 |
70 |
9423381.729 |
|
33 |
5897192.740 |
71 |
9444757.346 |
|
34 |
6072200.435 |
72 |
9465328.422 |
|
35 |
6246007.313 |
73 |
9486105.975 |
|
36 |
6417804.370 |
74 |
9512996.958 |
|
37 |
6587333.684 |
75 |
9584489.499 |
|
38 |
6752183.723 |
76 |
0 |
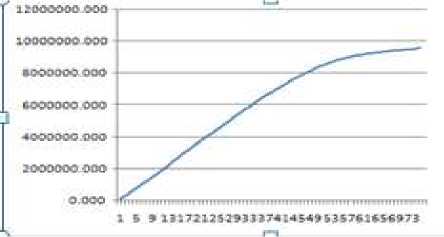
Gambar 1. Plot Hubungan antara Peningkatan Nilai Cadangan Premi dengan Periode Asuransi Jiwa.
Berdasarkan gambar 1, peningkatan nilai cadangan premi dari tahun ke 1 sampai tahun ke 56 proposional dengan peningkatan tahun, akan tetapi setelah tahun ke 56 peningkatan nilai cadangan premi mulai lambat.
Penelitian ini bertujuan untuk mendapatkan formula cadangan premi pada asuransi jiwa seumur hidup joint life. Metode yang digunakan untuk menentukan formula tersebut adalah metode premium sufficiency, yaitu metode perhitungan premi kotor. Pada penelitian ini menggunakan Tabel Mortalitas Indonesia (TMI) 2011, tingkat suku bunga sebesar 2,5% dan biaya alpha (a') = 0.05%. Hasil penelitian ini adalah berupa formula cadangan premi untuk asuransi jiwa seumur hidup joint life bagi pemegang polis berusia x tahun dan y tahun. Berdasarkan hasil simulasi, dapat dilihat pada grafik 1, peningkatan nilai cadangan premi dari tahun ke 1 sampai tahun ke 56 proposional dengan peningkatan tahun, akan tetapi setelah tahun ke 56 peningkatan nilai cadangan premi mulai lambat.
DAFTAR PUSTAKA
Futami, T., 1993. Matematika Asuransi Jiwa Bagian I. Herliyanto G, penerjemah. Tokyo (JP): Oriental Life Insurance Cultural
Development Center. Terjemahan dari: Seime Hoken Sugaku Gekan ("92 Revision).
_____,1994. Matematika Asuransi Jiwa Bagian 2. Herliyanto G, penerjemah. Tokyo (JP): Oriental Life Insurance Cultural Development Center. Terjemahan dari: Seime Hoken Sugaku Gekan ("92 Revision).
Siregar, M. T. 2014. Cadangan Asuransi Dwiguna Last Survivor dengan Metode Premium Sufficiency. JOM FMIPA , 447456.
Sembiring, R.K., 1986. Buku Materi
PokokAsuransi I. Jakarta: Universitas
Terbuka, Depdikbud.
Biro Pusat Aktuaria (Independent and
Trusted).,2012.Tabel Mortalita Taspen
2012. Jakarta: PT.Taspen,
https://ml.scribd.com/doc/211956752/TMT-2012, diakses tanggal 20 Juli 2015.
102
Discussion and feedback