PERAMALAN JUMLAH KUNJUNGAN WISATAWAN AUSTRALIA YANG BERKUNJUNG KE BALI MENGGUNAKAN MODEL TIME VARYING PARAMETER (TVP)

E-Jurnal Matematika Vol. 5 (3), Agustus 2016, pp. 117-125

ISSN: 2303-1751

PERAMALAN JUMLAH KUNJUNGAN WISATAWAN AUSTRALIA

YANG BERKUNJUNG KE BALI MENGGUNAKAN MODEL TIME VARYING PARAMETER (TVP)

I Putu Gede Dian Gerry Suwedayana^1§, I Wayan Sumarjaya², Ni Luh Putu Suciptawati³

¹Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: [email protected]] ²Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: [email protected]] ³Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: [email protected]] ^§Corresponding Author

ABSTRACT

The purpose of this research is to forecast the number of Australian tourists arrival to Bali ( Vt ) using Time Varying Parameter (TVP) model based on inflation of Indonesia (^lt) and exchange rate AUD to IDR ( ^21) from January 2010 – December 2015 as explanatory variables. TVP model is specified in a state space model and estimated by Kalman filter algorithm. The result shows that the TVP model can be used to forecast the number of Australian tourists arrival to Bali because it satisfied the assumption that the residuals are distributed normally and the residuals in the measurement and transition equations are not correlated. The estimated TVP model is ̂=201.8253^lt + 8.903399%2t. This model has a value of mean absolute percentage error (MAPE) is equal to 1.77% dan root mean square percentage error (RMSPE) is equal to 2.3418%. The number of Australian tourists arrival to Bali for the next five periods is predicted: 87,534; 86,708; 88,864; 90,651; and 88,077 (January - May 2016).

Keywords: time varying parameter model, state space model, Kalman filter, Australian tourists arrival to Bali

• 1.    PENDAHULUAN

Peramalan merupakan suatu proses untuk meramalkan sesuatu yang akan terjadi pada masa yang akan datang berdasarkan data pada masa lalu dengan menggunakan teknik atau cara tertentu (Siswanto, 2007). Peramalan ini dibuat sedemikian hingga dapat meminimumkan pengaruh ketidakpastian terhadap objek yang diramal. Pengaruh ketidakpastian ini bisa menjadi penyebab kesalahan ramalan (forecast error) yang biasanya diukur dengan mean absolute percentage error (MAPE), root mean squared percentage error (RMSPE), dan lain-lain.

Model ekonometrika merupakan suatu model yang sering dijumpai dalam peramalan. Salah satu contoh model ekonometrika adalah model Time Varying Parameter (TVP). Model TVP merupakan suatu model yang ditetapkan ke dalam suatu model state space dan diduga

dengan algoritma Kalman filter. Model state space ini mampu merepresentasikan variabel yang tidak teramati untuk ikut masuk ke dalam model dan diperkirakan bersama dengan model yang tampak. Tentu saja hal ini mampu mengurangi pengaruh ketidakpastian dalam peramalan. Selain itu pula penggunaan metode Kalman filter memberikan estimasi dengan cara yang dapat meminimumkan mean squared error sehingga memungkinkan mendapatkan hasil estimasi yang optimal (Welch & Bishop, 2001).

Model TVP sebagai suatu model ekonometrika tidak hanya dapat digunakan untuk memodelkan fenomena-fenomena ekonomi semata, namun juga dapat digunakan sebagai metode alternatif dalam memodelkan kunjungan wisatawan dan menghasilkan ramalan yang lebih akurat dibandingkan metode lainnya seperti Engle-Granger ECM, Wickens-Breusch ECM, Johansen vector error correction

model (VECM), autoregressive distributed lag model (ADLM), vector autoregressive (VAR), dan no-change model (Witt & Song, 2000). Selain itu, penelitian yang dilakukan oleh Song, et. al (2008), menunjukkan bahwa TVP memberikan akurasi yang paling akurat dalam peramalan jangka pendek (tiga periode ke depan) dibandingkan dengan model statistik regresi, Johansen Maximum Likelihood-ECM, Reduced ADLM, TVP, vector autoregressive (VAR), seasonal autoregressive integrated moving average (SARIMA), dan naïve. Dengan demikian model TVP dapat menjadi rekomendasi model untuk melakukan peramalan jumlah kunjungan wisatawan ke Bali.

Bali merupakan salah satu primadona daerah tujuan wisata di Indonesia yang mampu mendatangkan wisatawan domestik maupun mancanegara. Hal ini disebabkan daya tarik Bali yang memukau wisatawan, seperti budaya, adat istiadat, kesenian yang beraneka ragam, serta keindahan alamnya (Sri, 2013). Data statistik menunjukkan bahwa wisatawan Australia sebagai wisatawan mancanegara dengan jumlah kunjungan tertinggi (Dinas Pariwisata Provinsi Bali, 2016). Peramalan kunjungan wisatawan Australia ke Bali dipandang perlu dilakukan mengingat pariwisata di Bali berkontribusi besar dalam kehidupan masyarakat Bali dan juga berperan penting dalam meningkatkan Produk Domestik Regional Bruto (PDRB) Provinsi Bali.

Faktor kondisi ekonomi merupakan suatu faktor yang dipandang mempunyai pengaruh yang signifikan terhadap kunjungan wisatawan. Nilai tukar mata uang Australia terhadap rupiah dan inflasi yang terjadi di Indonesia merupakan pemberi andil dalam faktor ekonomi tersebut.

Model TVP dengan Kalman filter tidak membutuhkan asumsi bahwa data harus bersifat stasioner atau independen (Guo,1990). Dengan demikian, ketidakstasioneran data yang mungkin terjadi dari perubahan nilai tukar mata uang dan inflasi dari waktu ke waktu tersebut dapat diabaikan.

Kemungkinan yang dapat terjadi bila nilai mata uang negara Indonesia melemah terhadap mata uang Australia, maka wisatawan Australia merasakan murahnya berbelanja di Indonesia

(Wijaya, 2011). Sedangkan inflasi yang terjadi di Indonesia dapat menjadi representasi kenaikan harga seluruh komoditi termasuk di sektor pariwisata. Dengan demikian nilai tukar mata uang dan inflasi yang terjadi di Indonesia dapat memengaruhi jumlah kunjungan wisatawan Australia ke Bali.

Penelitian ini bertujuan untuk memodelkan jumlah wisatawan Australia yang berkunjung ke Bali menggunakan model TVP dan memprediksi jumlah wisatawan Australia yang berkunjung ke Bali. Peramalan jumlah kunjungan wisatawan Australia ke Bali dilakukan berdasarkan inflasi yang terjadi di Indonesia dan nilai tukar (kurs) AUD terhadap IDR.

• 2.    METODE PENELITIAN

Jenis data yang digunakan dalam penelitian ini adalah data sekunder. Data sekunder yang digunakan berupa data kunjungan wisatawan Australia ke Bali (y_t) yang diperoleh dari Dinas Pariwisata Provinsi Bali, inflasi yang terjadi di Indonesia (x₁₁), dan kurs AUD terhadap IDR (x₂ t) yang diperoleh dari Bank Sentral Republik Indonesia (BI) pada situs www.bi.go.id. Tahapan-tahapan analisis data dalam model TVP adalah sebagai berikut.

• 1.    Identifikasi Model TVP

Model TVP dinyatakan dalam bentuk state space sebagai berikut [12].

Persamaan pengukuran:

y_t -χ∣β_t+u_t ,                (1)

dan persamaan transisi:

βt = Φβt- 1 + Rt ^t ,              (2)

dengan y_t merupakan vektor Txl dari variabel terikat, x_t merupakan matriks Txk dari variabel-variabel penjelas, β_t merupakan vektor k x 1 dari parameter yang diketahui yang disebut sebagai state vector, Φ merupakan matriks transisi berukuran k × k, R_t merupakan matriks input yang menentukan struktur ragam dari persamaan transisi berukuran k × T, u_t merupakan vektor sisaan berukuran Txl dengan nilai tengah 0 dan matriks kovarians

Ht , dan e_t merupakan vektor sisaan T×1 dengan nilai tengah 0 dan matriks kovarians Qt.

Pada persamaan transisi, matriks Φ yang digunakan adalah matriks identitas, sehingga persamaan transisi menjadi random walk:

β_t = + R_te_t (3)

Dari persamaan pengukuran dan persamaan transisi, terdapat dua asumsi tambahan. Asumsi yang pertama bahwa vektor awal βo memiliki mean bo dan matriks kovarians Pq . Asumsi yang kedua, tidak terdapat korelasi antara sisaan dari u_t dan ^et dalam persamaan pengukuran dan persamaan transisi. Matriks ^xt , H_t , R^, dan Qt juga diasumsikan non-stokastik.

• 2.    Estimasi Menggunakan Algoritma Kalman Filter

Secara umum, estimasi menggunakan algoritma Kalman filter dapat dibagi menjadi tiga tahap, yaitu initial state, predict state, dan updates state. Tahap initial state dimulai dengan memberkan nilai awal ^O dan Pq . Jika state vector ^q dan matriks kovarians Pq tidak diketahui sebelumnya, maka Dq dan matriks kovarians Pq dapat diasumsikan nilainya dengan menggunakan metode diffuse priors. Prosedur pengoperasian metode diffuse priors adalah dengan memberikan nilai awal yang besar terhadap matriks kovarians P, saat nilai awal untuk koefisien dari variabel penjelas dipilih secara acak (Witt & Song, 2000). Nilai awal dari Pq ditetapkan sama dengan κl , dengan κ merupakan suatu nilai yang besar yang berhingga dan I merupakan matriks identitas berukuran k×k . Kisaran nilai κ berada anatara 10² dan 10⁷ (Casals, et al, 2000).

Tahap predict state, estimasi dimulai dari t-1, kemudianb_t |t —1 dan P_t |t —1 dapat dihitung dari persamaan berikut (lihat Witt & Song, 2000).

b_t|t-i=Φb_t-ι , (4)

P_t | =ΦPt-IΦ ′+RtQtRt′ . (5)

Setelah memperoleh nilai bt|t ^—1 dan P_t | 1 , selanjutnya dapat diduga nilai yt berdasarkan informasi pada t-1 sebagai berikut.

• ̂t| t-l =      | t-l .(6)

Prediction error dari yt dapat dihitung dengan rumus

n=    - ̂t| t-l .(7)

dan mean squared error (MSE) dari Vt diperoleh dari rumus

Ft =     |t-ι^xt′+ ∏t .(8)

Tahap updates state, pada saat suatu amatan awal ( t-1) diperoleh, maka penduga state vector dapat diperbarui. Proses updates state ini dapat dituliskan sebagai berikut.

b_t =   |t-i + P_t |t-l^xt′F_t~¹ (yt-Φb_t |t-i),(9)

dan

Pt =   | t-l ^- Pt | t-ι^χ_t′F_t ^lχ_tPt| t-i .   (10)

Proses pembaruan tersebut, merupakan proses pembaruan dengan menggunakan Kalman gain ( Kt). Proses Kalman gain tersebut termuat dalam persamaan bt dan P_t , yaitu

Kt =   |t-ι^xt′F_t~¹ .                 (11)

• 3.    Kriteria Peramalan

Kriteria yang digunakan untuk menguji ketepatan ramalan adalah mean absolute percentage error (MAPE) dan root mean square percentage error (RMSPE). Sebagai suatu kriteria dalam menguji ketepatan model,    MAPE    dan    RMSPE

merepresentasikan model yang dibuat bahwa semakin kecil nilai MAPE dan RMSPE, maka semakin baik model yang digunakan. MAPE dan RMSPE dapat dituliskan sebagai berikut:

_∑m^| ≤t ^|

∑t=0

MAPE ₌      ,          (12)

RMSPE =√ ^∑ Z₀ ⁽ ‘i ) ,  (13)

dengan m merupakan banyak data pada periode yang digunakan, e_t merupakan galat dari peramalan, dan Y_t merupakan nilai sebenarnya dari variabel jumlah kunjungan wisatawan Australia.

• 4.    Uji Diagnostik

Uji diagnostik dilakukan untuk mengetahui sisaan dari model berdistribusi normal dan tidak terdapat korelasi antara sisaan pada persamaan pengukuran dan sisaan pada persamaan transisi. Untuk mengetahui sisaan berdistribusi normal dilakukan dengan uji Kolmogorov-Smirnov. Pengujian ini dilakukan karena penggunaan Kalman filter bergantung pada asumsi sisaan data berdistribusi normal (Bernard, et al, 2010). Hipotesis dalam pengujian ini adalah sebagai berikut.

Hq : Sisaan berdistribusi normal

Hγ : Sisaan tidak berdistribusi normal

Statistik uji Kolmogorov-Smirnov adalah

D =sup_x|N(x)-N₀ (x)|      (14)

dengan N(x) menyatakan fungsi fre kuensi kumulatif yang dihitung dari data sampel, Nq (X) menyatakan fungsi distribusi frekuensi kumulatif distribusi normal, dan sup_x merupakan nilai maksimum dari |N(x)-Nq (X)| untuk semua x. Keputusan Hq ditolak apabila ^hit >      , atau nilai

p-value< a, dengan      CC adalah tabel

Kolmogorov-Smirnov pada kuantil (1-a).

Model TVP mengasumsikan tidak terdapat korelasi antara sisaan pada persamaan pengukuran dan persamaan transisi. Untuk melihat suatu tidak terdapat korelasi antara sisaan pada persamaan pengukuran dan persamaan transisi digunakan koefisien korelasi Pearson. Hipotesis pengujian ini adalah sebagai berikut.

Hq :    =0 (tidak terdapat korelasi antaraX

dan Y),

H^ :    ≠0 (terdapat korelasi antaraX dan

y).

Statistik uji yang digunakan adalah

^hitung = ^y= ^√ —                (15)

√ 1 ^rxy

dengan

⁼

________n^∑ ^^xt^γj- ^∑ ‰Xj ^∑i=ι ^γi________

√(n^∑7=ι^χι² (∑7=ι^χι)²)(n^∑F=I ^yI² (∑F=I ^yI)²)

(16)

dan n menyatakan banyaknya observasi pengamatan. Keputusan Hq ditolak apabila | t hitung|>ta n-2atau р-value<a.

2;

• 5.    Peramalan

Peramalan m periode kedepan untuk b, P , dan y dapat diperoleh dengan menggunakan persamaan berikut.

bτ+m|T=Φbτ+m-ι ,(17)

^T+m |

^Φ Pτ+m-ι|TΦ ′+Pτ+mQτ+mPτ+m′ ,(18)

̂T+m|T⁼             |T .(19)

• 3.    HASIL DAN PEMBAHASAN

Identifikasi Model TVP

Pada tahap ini terlebih dahulu dilakukan plot data jumlah kunjungan wisatawan Australia ke Bali, inflasi yang terjadi di Indonesia dan kurs AUD terhadap IDR bulan Januari 2010 –

Desember 2015. Langkah ini dilakukan untuk menunjukan secara deskriptif bahwa data yang dianalisis adalah data yang bersifat time varying (berubah-ubah) bergantung pada waktu. Hasil plot data jumlah kunjungan wisatawan Australia ke Bali, inflasi yang terjadi di Indonesia, dan kurs AUD terhadap IDR secara berturut-turut dapat dilihat pada Gambar 1, Gambar 2 dan Gambar 3.

W ISATAWAN

110,000

100,000

90,000

80,000

70,000

60,000

50,000

40,000

30,000

2010     2011     2012     2013    2014    2015

Gambar 1. Plot Data Jumlah Kunjungan Wisatawan Australia ke Bali

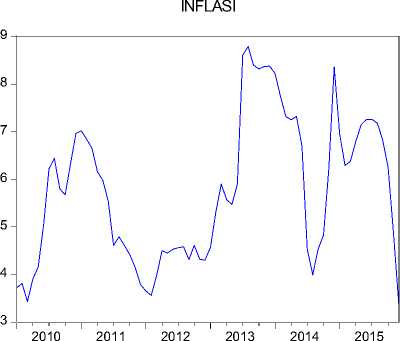
Gambar 2. Plot Data Inflasi di Indonesia

KURS

11,200

10,800

10,400

10,000

9,600

9,200

8,800

8,400

8,000

7,600

Gambar 3. Plot Data Kurs AUD terhadap IDR

Hasil plot data jumlah kunjungan wisatawan Australia ke Bali, inflasi yang terjadi di Indonesia dan kurs AUD terhadap IDR bulan Januari 2010 – Desember 2015 menunjukkan bahwa variabel yang digunakan bersifat time varying. Dengan demikian maka variabel-

2010     2011     2012     2013     2014     2015

variabel tersebut relevan digunakan dalam model TVP.

Spesifikasi model TVP dari kunjungan wisatawan Australia dalam bentuk state space dapat dinyatakan sebagai berikut.

Persamaan pengukuran:

Vt ⁼       + β2t^x2t + u_t           (20)

Persamaan transisi:

βit ⁼      + Sit                     (21)

dengan i=1 dan 2.

Persamaan pengukuran mendefinisikan hubungan antara variabel kunjungan wisatawan Australia (y_t) dengan variabel penjelasnya yaitu inflasi yang terjadi di Indonesia (^xU ) dan kurs AUD terhadap IDR ( %2t).   Sedangkan

persamaan transisi menggambarkan pergerakan dari parameter yang berubah-ubah setiap waktu. Misalkan bit dan P_t secara berturut-turut merupakan state vector dan kovarians yang menunjukkan penduga optimal dari βit .

Estimasi Parameter

Estimasi maximum likelihood dengan menggunakan bantuan Eviews 6 diperoleh kovarians dari persamaan pengukuran yaitu bit = 1,713811 dan kovarians persamaan transisi dari state vector b It dan ^2t yaitu:

0,000469     0

Qt^=*   0      1,721011⁺

berdasarkan Tabel 1 berikut.

Tabel 1. Nilai Kovarians dengan Estimasi Maximum Likelihood

Nilai Struktural Kovarians
	State Vector 1	State Vector 2	Persamaan pengukuran
State Vector 1	0,000469	0,000000	0,000000
State Vector 2	0,000000	1,721011	0,000000
Persamaan pengukuran	0,000000	0,000000	1,713811

Berdasarkan nilai kovarians Ht dan Qt , dilakukan estimasi dengan menggunakan algoritma Kalman filter untuk memperoleh state vector dan kovarians dari βt . Tahap initial state dimulai dengan memberikan nilai awal ^O dan

P₀. Pada program Eviews 6, state vector bι₀ diberikan nilai awal 0 untuk i = 1 dan 2 serta matriks kovarians P₀ diasumsikan nilainya dengan menggunakan metode diffuse priors yaitu *θ 0+ dengan κ = 10⁶. Hasil estimasi Kalman filter dengan menggunakan program Eviews 6 ditunjukkan pada Tabel 2.

Tabel 2. Hasil Estimasi Model State Space dengan Algoritma Kalman Filter

	State Akhir	Statistik Uji z	p-value
State Vector 1	201,8253	0,182985	0,8548
State Vector 2	8,903399	6,534689	0,0000

Berdasarkan Tabel 2 diperoleh hasil state vector b₁₁ = 201,8253 dan state vector b2 t = 8,903399. Dengan demikian, estimasi model TVP kunjungan wisatawan Australia ke Bali dapat dinyatakan sebagai berikut.

y_t = 201,8253%_{1 t} + 8,903399%_{2 t} . (22)

Nilai b_{1 t} = 201,8253 mengindikasikan jika inflasi yang terjadi di Indonesia meningkat 1% maka jumlah kunjungan wisatawan Australia akan meningkat sebesar 201,8253 ≈ 202 orang dengan nilai kurs AUD terhadap IDR diasumsikan konstan. Namun, inflasi tersebut menghasilkan nilai p-value (0,8548) > α (0,05), dengan demikian nilai inflasi tersebut tidak berpengaruh secara signifikan terhadap jumlah kunjungan wisatawan Australia ke Bali. Sedangkan nilai b_{2 t} = 8,903399 berarti jika kurs AUD terhadap IDR meningkat 1 rupiah maka akan meningkatkan jumlah kunjungan wisatawan Australia sebesar 8,903399 ≈ 9 orang dengan inflasi yang terjadi di Indonesia diasumsikan konstan. Nilai kurs AUD terhadap IDR menghasilkan nilai p-value (0,0000) < α (0,05), hal ini berarti menguatnya nilai tukar AUD terhadap IDR berpengaruh secara signifikan terhadap jumlah kunjungan wisatawan Australia ke Bali.

Estimasi dengan algoritma Kalman filter tersebut menghasilkan matriks kovarians akhir β yaitu:

1216468,  -405,64461

^t = [-405,6446   1,856278 J'

SV1F

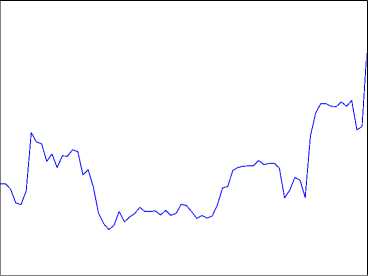
2010    2011     2012    2013    2014    2015

Plot Data State Vector

Berdasarkan estimasi dengan menggunakan algoritma Kalman filter diperoleh state vector dari bulan Januari 2010 sampai bulan Desember 2015 pada gambar 4 dan gambar 5. Langkah ini dilakukan untuk menunjukan secara deskriptif bahwa data state vector yang dianalisis masih mengandung parameter yang cenderung bersifat time varying (berubah-ubah) bergantung pada waktu.

800

600

400

200

0

-200

-400

Gambar 4. Plot Data State Vector 1 Bulan Januari 2010 - Desember 2015

10

8

6

4

2

0

Gambar 5. Plot Data State Vector 2 Bulan Januari 2010 - Desember 2015

Gambar 4 menunjukkan bahwa state vector b i t yang dilambangkan dengan SVlF tersebut mempunyai pergerakan yang cenderung berubah dari waktu ke waktu atau bersifat time varying. Sedangkan state vector b2 _t yang dilambangkan dengan SV2F ditunjukkan pada Gambar 5 mempunyai pergerakan yang cenderung berubah dari waktu ke waktu atau bersifat time varying.

SV2F

AyWwM

2010    2011     2012     2013    2014    2015

Kriteria Peramalan

Kriteria yang digunakan untuk menguji ketepatan ramalan dari estimasi model TVP adalah mean absolute percentage error (MAPE) dan root mean square percentage error (RMSPE). Diperoleh nilai ∑^l ^| ^^| = 1,27437 ^γt 2

dan ∑^l (I ) = 0,03948 dengan m=72.

Dengan demikian diperoleh nilai MAPE dan RMSPE sebagai berikut.

_∑m| ^t |

∑t=iγ. 1.2 743 7    __..

MAPE ₌      = ^,    = 0,0177 = 1,77%,

RMSPE⁼√ ^1∑  ₍I⁾ =√₇¹₂(0,03948)

= 0,023418 = 2,3418%.

Nilai ini mengindikasikan tingkat kesalahan yang dapat terjadi pada peramalan kunjungan wisatawan Australia menggunakan model TVP. Hal ini berarti semakin kecil nilai MAPE dan RMSPE maka semakin baik model yang digunakan. Nilai MAPE = 1,77% dan RMSPE = 2,3418% berada di bawah nilai 10%, hal ini berarti estimasi model tersebut sangat akurat dalam melakukan peramalan (Zhang, et. al, 2015).

Uji Diagnostik

Uji diagnostik dilakukan untuk mengetahui sisaan dari model berdistribusi normal dan tidak terdapat korelasi antara sisaan pada persamaan pengukuran dan sisaan pada persamaan transisi. Untuk mengetahui sisaan berdistribusi normal dilakukan dengan uji Kolmogorov-Smirnov. Hipotesis dalam pengujian ini adalah sebagai berikut.

Hq : Sisaan berdistribusi normal,

H^ : Sisaan tidak berdistribusi normal.

Berdasarkan data residual model TVP dan berdasarkan persamaan (14), hasil uji Kolmogorov-Smirnov bisa dilihat pada Tabel 3.

Tabel 3. Hasil Uji Kolmogorov-Smirnov

Uji Kolmogorov-Smirnov	Dhit	р-value
Sisaan Pengukuran	0,084	0,200

Berdasarkan tabel Kolmogorov-Smirnov pada kuantil 0,95 dengan nilai        ⁼

0,15755 dan berdasarkan Tabel 3 tampak bahwa sisaan dari model TVP memiliki nilai Dhi_t(0,084) < Stable, yang dipertegas lagi dengan nilai p-value = 0,200 > 0,05. Oleh karena itu, tidak terdapat cukup bukti untuk menolak Hq . Dengan demikian, dapat disimpulkan bahwa model TVP memiliki sisaan yang berdistribusi normal.

Untuk melihat tidak terdapatnya korelasi antara sisaan pada persamaan pengukuran dan persamaan transisi digunakan koefisien korelasi Pearson. Hipotesis pengujian ini adalah sebagai berikut.

Hq :      =0, untuki=1 dan 2 (tidak terdapat

korelasi antara u_t dan ^eit ),

H^ :      ≠0 (terdapat korelasi antara u_t dan

Si_t).

Tabel 4. Hasil Analisis Koefisien Korelasi Pearson

		Sisaan State Vector 1	Sisaan State Vector 2
Sisaan pengukuran	Korelasi Pearson	-0,04	0,114
	р-value	0,739	0,339

Hasil korelasi Pearson bisa dilihat pada Tabel 4. Luaran tersebut menghasilkan nilai korelasi Pearson antara sisaan persamaan pengukuran (resid) dengan persamaan transisi ^eU (esv1) sebesar -0,040. Dengan demikian dapat dicari statistik uji yang digunakan, yaitu:

t .    - ^rJUSit √n-2   -0,040√72 - 2

t hitung ⁼ √1-      ⁼ √1 - (-0,040)⁵

√1-

= -0,33493

Nilai | t hitung|=0,33493<to, ;     =

2 ;

2,6479, hal ini berarti tidak terdapat cukup bukti untuk menolak hipotesis Hq . Dengan demikian dapat disimpulkan bahwa tidak terdapat korelasi antara sisaan pada persamaan pengukuran dengan sisaan pada persamaan transisi ^lt .

Selain itu, luaran tersebut menghasilkan nilai korelasi Pearson antara sisaan persamaan

pengukuran (resid) dengan persamaan transisi ^2t (esv2) sebesar 0,114. Dengan demikian dapat dicari statistik uji yang digunakan, yaitu:

t .    - ^t^t √n-2   0.114√72 - 2

^hitung ⁼ √1-     ⁼√1-(0.114)

√1-

= 0.960051

Nilai | ^hitung |=0,960051<to, ;     =

2 ;

2,6479, hal ini berarti tidak terdapat cukup bukti untuk menolak hipotesis Hq . Dengan demikian dapat disimpulkan bahwa tidak terdapat korelasi antara sisaan pada persamaan pengukuran dengan sisaan pada persamaan transisi β2t.

Jadi, model TVP memiliki sisaan yang berdistribusi normal dan tidak terdapat korelasi antara sisaan persamaan pengukuran dan persamaan transisi, sehingga model layak untuk digunakan. Oleh karena itu, model TVP yang terdapat pada persamaan (22) dapat digunakan untuk melakukan peramalan jumlah kunjungan wisatawan Australia ke Bali.

Peramalan dengan Model TVP

Berikut hasil ramalan kunjungan wisatawan Australia yang berkunjung ke Bali estimasi model TVP pada persamaan (22) dari bulan Januari 2016-Mei 2016.

Tabel 5. Peramalan Jumlah Kunjungan Wisatawan Australia ke Bali dengan Model TVP

Bulan	Inflasi* (Xit)	Kurs* (x2t)	Peramalan Wisatawan AUS ( ̂ )	Jumlah Wisatawan AUS (yt)**
Jan-16	4,14	9.737,67	87.534	87.893
Peb-16	4,42	9.638,56	86.708	68.269
Mar-16	4,45	9.880,05	88.864	86.748
Apr-16	3,6	10.100,00	90.651	93.040
Mei-16	3,33	9.817,05	88.077	92.977

Sumber:

* Data inflasi dan kurs: Bank Sentral Indonesia (2016)

**Data jumlah wisatawan Australia: Dinas Pariwisata Provinsi

Bali (2016)

• 4.    KESIMPULAN DAN SARAN

Berdasarkan hasil dan pembahasan yang telah dipaparkan sebelumnya, diperoleh estimasi model TVP jumlah kunjungan wisatawan

Australia yang berkunjung ke Bali dengan variabel penjelas inflasi yang terjadi di Indonesia dan kurs AUD terhadap IDR sebagai berikut.

̂ = 201,8253Xit + 8,903399X_2t .

Model tersebut memiliki nilai MAPE = 1,77% dan RMSPE = 2,3418%. Nilai-nilai tersebut menunjukkan nilai MAPE dan RMSPE yang lebih kecil dari 10% yang berarti tingkat keakuratan model sangat baik dalam melakukan peramalan. Peramalan jumlah kunjungan wisatawan Australia yang berkunjung ke Bali lima periode ke depan yaitu dari bulan Januari-Mei 2016 diperoleh hasil secara berturut-turut, yaitu 87.534, 86.708, 88.864, 90.651, dan

88.077 wisatawan Australia.

Saran untuk penelitian selanjutnya yaitu diharapkan untuk dapat menggunakan spesifikasi persamaan transisi yang lainnya seperti:

βt = -Φ (βt-ι ^-μ)+Rte_t

dengan V^t- merupakan nilai tengah dari βt . Sehingga nantinya dapat dibandingkan hasil yang diperoleh dengan penelitian ini yang menggunakan spesifikasi persamaan transisi berupa random walk.

DAFTAR PUSTAKA

Bank Sentral Indonesia. 2016. Kalkulator Kurs.

Diakses     4     Juni     2016,     dari

http://www.bi.go.id/id/moneter/kalkulator-kurs/Default.aspx

_______.  2016. Data Inflasi. Diakses 4 Juni 2016, dari http://www.bi.go.id/id/moneter /inflasi/data/Default.aspx

Bernard, J.-T., Dufour, J. M., & Khalaf, L. 2010. An Identification-Robust Test for Time Varying Parameter in the Dynamics of Energy   Prices.   Journal of Applied

Econometrics, Volume 27, Issue 4, pp. 603624.

Casals, J., Jerez, M., & Sotoca, S. 2000. Exact Smoothing for Stationary and Nonstationary Time Series. International Journal of Forecasting, Volume 16, No. 1, pp. 59-69.

Dinas Pariwisata Provinsi Bali. 2016. Kedatangan Wisatawan Mancanegara yang Langsung ke Bali Berdasarkan Kebangsaan Setiap Bulan. Diakses 26 Maret 2016, dari www.disparda.baliprov.go.id

Guo, L. 1990. Estimating Time-Varying Parameter by the Kalman Filter Based Algorithm: Stability and Convergence. IEEE Transactions on Automatic Control, Volume 35, No. 2, pp. 141-147.

Siswanto. 2007. Operations Research. Jakarta: Erlangga.

Song, H., Smeral, E., Li, G., & Chen, J. L. 2008. Tourism Forecasting:   Accuracy of

Alternative Econometric Models Revisited. WIFO Working Papers.

Sri, A. A. P. 2013. Faktor-Faktor yang Memotivasi Perempuan Sebagai Pengelola Pondok Wisata di Kelurahan Ubud, Kecamatan Ubud, Kabupaten Gianyar. Jurnal Analisis Pariwisata. Volume 13, No. 1, pp. 1-118.

Welch, G., & Bishop, G. 2001. An Introduction to the Kalman Filter. Siggraph 2001 Course 8.

Wijaya, I N. 2011. Pengaruh Jumlah Wisatawan Mancanegara, Lama Tinggal dan Kurs Dolar Amerika Terhadap Penerimaan Produk Domestik Regional Bruto Industri Pariwisata Kabupaten Badung Tahun 19972010. Tesis S2 Program Studi Kajian Pariwisata. Denpasar: Universitas Udayana.

Witt, S. F., & Song, H. 2000. Advances in Tourism Research:  Tourism  Demand

Modelling and Forecasting:  Modern

Econometric Approaches. New York, USA: Routledge.

Zhang, T., Wang, K., & Zhang, X. 2015. Modeling and Analyzing the Transmission Dynamics of HBV Epidemic in Xinjiang, China. Journal PLOS One. Volume 10, No. 9, pp. 1-14.

125