PENERAPAN METODE FUZZY AHP DALAM PENENTUAN SEKTOR YANG BERPENGARUH TERHADAP PEREKONOMIAN PROVINSI BALI
on
E-Jurnal Matematika Vol. 5 (2), Mei 2016, pp. 59-66
ISSN: 2303-1751
PENERAPAN METODE FUZZY AHP DALAM PENENTUAN
SEKTOR YANG BERPENGARUH TERHADAP PEREKONOMIAN PROVINSI BALI
Tjokorda Gde Agung Friska Adnyana§1, G. K. Gandhiadi2, Desak Putu Eka Nilakusmawati3
-
1Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: cokfriska55d.excel@gmail.com] 2Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: gandhiadigk@yahoo.com] 3Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: nilakusmawati@unud.ac.id]
§Corresponding Author
ABSTRACT
The aim of this research is to apply Fuzzy Analytic Hierarchy Process method to determine the dominant sectors of economy Bali Province. This research used survey data from respondents who understand about economy of Bali Province and Gross Regional Domestic Product (GRDP). The research variables consist of criteria and sub-criteria. The criteria consist of primary sector, secondary, and tertiary, while the sub-criteria consist of 9 sectors of the GRDP. Data processing is done by calculating the weighted average and arrange them into pairwise comparison matrices. Furthermore, the consistency ratio is checked. If consistency ratio less than 0.100 (CR < 0.1), the elements of matrices is changed into triangular fuzzy scale and processed with synthetic extent to get the priority. Based on the result of research, the economy of Bali are dominated by tertiary sector in sector group, agriculture and forestry in sub-primary group, manufacturing industry in subsecondary group, and trade, hotel and restaurant in sub-tertiary group..
Keywords: Economy, Sector, Fuzzy Analytic Hierarchy Process
dikembangkan teori lebih lanjut yaitu metode Fuzzy Analytic Hierarchy Process.
Fuzzy Analytic Hierarchy Process adalah metode Analytic Hierarchy Process (AHP) yang dikembangkan dengan teori logika fuzzy, khususnya triangular fuzzy. Langkah penyelesaian masalah dengan metode Fuzzy AHP hampir sama dengan metode AHP. Hanya saja metode Fuzzy AHP mengubah skala AHP ke dalam skala triangular fuzzy untuk memperoleh prioritas. Selanjutnya, menurut Chang [2] data yang telah diubah tersebut diproses lebih lanjut dengan extent analysis.
Pada penelitian ini penulis mencoba menerapkan metode Fuzzy AHP pada kasus perekonomian Provinsi Bali. Penerapan metode fuzzy AHP digunakan untuk mengetahui sektor-sektor yang berkontribusi dominan terhadap perekonomian Provinsi Bali.
Adapun komponen perekonomian Bali terdiri atas sektor dan subsektor. Sektor
merupakan pengelompokan ekonomi menurut aktivitas yang terdiri dari sektor primer, sektor sekunder dan sektor tersier. Sektor primer terdiri atas tiga subsektor yaitu (1) pertanian dan kehutanan, (2) peternakan dan perikanan, dan (3) pertambangan dan penggalian. Sektor sekunder terdiri atas tiga subsektor yaitu (1) industri pengolahan, (2) listrik, gas dan air bersih, dan (3) konstruksi. Sektor tersier terdiri atas empat subsektor yaitu (1) perdagangan, hotel dan restoran, (2) pengangkutan dan komunikasi, (3) keuangan, persewaan dan jasa perusahaan, dan (4) jasa-jasa.
Saaty & Kearns [5] menjelaskan bahwa terdapat tiga prinsip dasar dalam metode AHP, yaitu dekomposisi, perbandingan penilaian, dan sintesis prioritas. Dekomposisi adalah langkah memecah atau membagi masalah menjadi suatu struktur hirarki. Struktur tersebut terdiri dari tiga tingkat yaitu tingkat pertama (tujuan), tingkat kedua (kriteria) dan tingkat ketiga (alternatif).
Selanjutnya, perbandingan penilaian dilakukan dengan membandingkan kriteria secara berpasangan dan diukur dengan skala perbandingan dari 1 sampai dengan 9. Bobot penilaian yang diperoleh kemudian disusun ke dalam matriks perbandingan berpasangan dan dilakukan proses sintesis untuk memperoleh nilai masing-masing kriteria. Nilai masing-masing kriteria didapat dengan menghitung vektor prioritas (vektor eigen) dari matriks perbandingan berpasangan.
Misalkan terdapat sebanyak n kriteria (^l , ^2 ,…,A∏) dengan —(i=1,2,…,n, = Wj
-
1,2,…,n) adalah bobot perbandingan berpasangan, maka dapat disusun matriks perbandingan berpasangan seperti Tabel 1.
Tabel 1. Matriks Perbandingan Berpasangan
|
A2 | ||||
|
j4ι |
W1 W1 |
W1 W2 |
W1 Wn | |
|
W2 W1 |
W2 W2 |
W2 W„ | ||
|
^n |
Wn W1 |
Wn W2 |
Wn Wn | |
|
Sumber: Saaty & Kearns (1985) | ||||
Selanjutnya dilakukan pengujian untuk mengetahui kekonsitenan dari penilaian. Pengujian konsistensi matriks berukuran n×n diperoleh dengan persamaan berikut (Saaty & Kearns [5])
=( ^nax -n)
= (n-1) (1)
dengan, CI = Rasio penyimpangan (deviasi) konsistensi (consistency index)
^max = Nilai eigen terbesar dari matriks berordo n
n = Banyak kriteria
Batas ketidakkonsistenan (inconsistency) ditentukan dengan menggunakan Rasio Konsistensi (CR), yaitu perbandingan indeks konsistensi (CI) dengan nilai random index (RI) yang diperlihatkan pada Tabel 2. Nilai ini bergantung pada n. Dengan demikian, Rasio Konsistensi dirumuskan sebagai berikut (Saaty & Kearns [5])
CI
CR = (2)
CR = Consistency Ratio
RI = Random Index
Tabel 2. Nilai Random Index (RI)
|
N |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
RI |
0. 00 |
0. 00 |
0. 52 |
0. 89 |
1. 11 |
1. 25 |
1. 35 |
1. 40 |
1. 45 |
1. 49 |
Sumber: Saaty & Vargas (2001)
Bila matriks pairwise comparison mempunyai nilai CR < 0.100 maka ketidakkonsistenan pendapat dari pengambil keputusan dapat diterima, dan apabila nilai tidak terpenuhi maka penilaian harus diulang.
Saat kondisi konsisten terpenuhi maka dilanjutkan dengan pembobotan skala triangular fuzzy number (Tabel 3).
Tabel 3. Skala AHP dan Triangular Fuzzy Number
|
Skala AHP |
Skala Fuzzy |
Invers Skala Fuzzy |
Keterangan |
|
1 |
(1,1,1) |
(1,1,1) |
Sama Penting |
|
2 |
(1,2,3) |
(13,12,1) |
Skala antara sama dan sedikit lebih penting |
|
3 |
(2,3,4) |
(14,13,12) |
Sedikit lebih penting |
|
4 |
(3,4,5) |
111 (5,4,3) |
Skala antara sedikit lebih dan lebih penting |
|
5 |
(4,5,6) |
111 (6,5,4) |
Lebih penting |
|
6 |
(5,6,7) |
111 (7,6,5) |
Skala antara lebih dan sangat penting |
|
7 |
(6,7,8) |
111 (8,7,6) |
Sangat penting |
|
8 |
(7,8,9) |
111 (9,8,7) |
Skala antara sangat dan mutlak lebih penting |
|
9 |
(8,9,9) |
111 (9,9,8) |
Mutlak lebih penting |
Sumber: Hsu, et al (2010)
V (Si ≥ S2 )
Chang [2] menjelaskan langkah-langkah metode Fuzzy AHP sebagai berikut
-
1) Menghitung nilai fuzzy synthetic extent
j-i i-ij=ι
dengan
∑ Mgi=(∑1I ,∑mj,∑Uj )
dan ⨂ merupakan operator dot product. Sedangkan untuk memperoleh nilai [∑ F=I ∑l=JMgi] dilakukan operasi penjumlahan untuk keseluruhan bilangan triangular fuzzy Mg.( =1,2,…,m) yaitu:
∑∑ =
i=ιj=i
Jadi
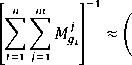
∑F=I ∑ "
-
2) Menghitung perbandingan tingkat kemungkinan antara bilangan fuzzy
Untuk dua bilangan triangular fuzzy ∙S"ι =( ^i , m1 , U1 ) dan $2=( ^2 , m2 , U2 ) dengan tingkat kemungkinan ( 1^l ≥ ¾ ) dapat didefinisikan oleh persamaan berikut:
⎧111111111111, jika m1 ≥ JU2
00000000000, jika I2 ≥ U1
I2 - U1 (4)
, lainnya
(ITl1 - U1)-(^2 - I2 )
-
3) Menghitung tingkat kemungkinan untuk bilangan fuzzy
Tingkat kemungkinan bilangan fuzzy didefinisikan sebagai berikut
d’ (A)=minV(Si ≥ Sk) (5)
k=1,2,…,n;k≠i
Sehingga diperoleh vektor bobot
W'=(d’ (A1), d’ (A2),…,d’ (An)) T
-
4) Menormalisasi vektor bobot
Vektor bobot yang masih dalam bentuk bilangan fuzzy selanjutnya dinormalisasi dengan persamaan
d(Ai)
d'( di )
∑l=ld'(Ai)
(6)
,∑r=1 ∑7m=1
,∑r=1 ∑T=A
untuk i=1,2,…,n
Penelitian ini menggunakan data berupa data primer. Data diperoleh melalui survey dengan menyebarkan kuesioner kepada 50 orang responden. Responden berasal dari beberapa instansi yaitu kantor Badan Pusat Statistik (BPS) Provinsi Bali, BPS Kabupaten/Kota di Bali, Badan Perencanaan
Pembangunan Daerah (Bappeda) Provinsi Bali, dan akademisi dari Fakultas Ekonomi Universitas Udayana dengan teknik pengambilan sampel yang digunakan adalah purposive sampling. Adapun langkah-langkah penelitian ini adalah sebagai berikut:
-
1. Merata-ratakan hasil dari masing-masing
kriteria untuk memperoleh bobot yang akan dibentuk ke dalam matriks perbandingan berpasangan.
-
2. Menyusun matriks untuk masing-masing
kelompok.
-
3. Menghitung nilai eigen maksimum dan
menguji konsistensi.
-
4. Jika hasil uji konsistensi memenuhi < 0.100, maka bobot diubah ke dalam skala triangular fuzzy (Tabel 3).
-
5. Apabila tidak terpenuhi < 0.100 maka penilaian diulang dengan perbaikan perbandingan berpasangan.
-
6. Menghitung nilai fuzzy synthetic extent menggunakan persamaan (3).
-
7. Membandingkan nilai fuzzy synthetic extent dengan persamaan (4).
-
8. Mengambil nilai minimum dari perbandingan nilai fuzzy synthetic extent menggunakan persamaan (5).
-
9. Menormalisasi vektor bobot dengan persamaan (6) untuk memperoleh kriteria prioritas.
Berdasarkan permasalahan diperoleh struktur hirarki (Gambar 1)
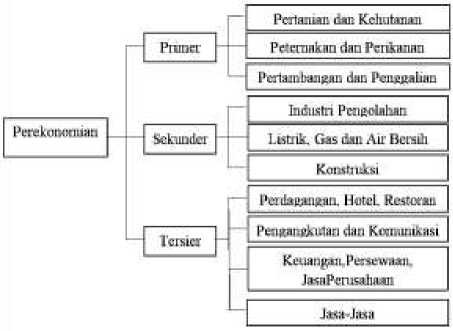
Gambar 1. Struktur Hirarki Perekonomian
Selanjutnya kriteria dalam satu kelompok dibandingkan secara berpasangan dan diberi bobot penilaian. Pada penelitian ini, dengan mengadopsi skala kepentingan yang dijelaskan oleh Saaty [6] didefinisikan skala tingkat dominan dan variabel penelitian sebagai berikut Tabel 4. Skala Tingkat Dominan
|
Tingkat Dominan |
Definisi |
|
1 |
Sama dominan |
|
3 |
Sedikit dominan |
|
5 |
Cukup dominan |
|
7 |
Lebih dominan |
|
9 |
Mutlak lebih dominan |
|
2,4,6,8 |
Nilai diantara dua pilihan yang berdekatan |
Tabel 5. Variabel Penelitian
|
No |
Kriteria |
Variabel |
|
1 |
Primer |
P |
|
2 |
Sekunder |
S |
|
3 |
Tersier |
T |
|
4 |
Pertanian dan Kehutanan |
SP1 |
|
5 |
Peternakan dan Perikanan |
SP2 |
|
6 |
Pertambangan dan Penggalian |
SP3 |
|
7 |
Industri Pengolahan |
SS1 |
|
8 |
Listrik, Gas, Air Bersih |
SS2 |
|
9 |
Konstruksi |
SS3 |
|
10 |
Perdagangan, Hotel, Restoran |
ST1 |
|
11 |
Pengangkutan dan Komunikasi |
ST2 |
|
12 |
Keuangan, Persewaan dan Jasa Perusahaan |
ST3 |
|
13 |
Jasa-jasa |
ST4 |
Data bobot yang diperoleh selanjutnya dirata-ratakan dan dibulatkan ke bobot AHP. Hasil bobot yang telah dirata-ratakan disajikan pada Tabel 6.
Sebagai penjelasan Tabel 6:
-
■ Bobot rata-rata Primer: Sekunder adalah 3.4420, hasil ini menyatakan bahwa reponden menilai sektor primer berkontribusi sedikit dominan dibandingkan sektor sekunder, dengan bobot AHP adalah 3.
-
■ Bobot rata-rata Pertanian, Kehutanan : Peternakan, Perikanan adalah 3.3468, hasil ini menyatakan bahwa reponden menilai pertanian dan kehutanan berkontribusi sedikit dominan dibandingkan peternakan dan perikanan, dengan bobot AHP adalah 3
Tabel 6. Hasil Penilaian Responden
|
No |
Perbandingan Kriteria |
Bobot Rata-rata |
Bobot AHP | ||||||||
|
1 |
Primer : Sekunder |
3.4420 |
3 | ||||||||
|
2 |
Primer : Tersier |
0.4833 |
1/2 | ||||||||
|
3 |
Sekunder : Tersier |
0.2317 |
1/4 | ||||||||
|
Subsektor Primer | |||||||||||
|
4 |
Pertanian, Kehutanan : Peternakan, Perikanan |
3.3468 |
3 | ||||||||
|
5 |
Pertanian, Kehutanan : Pertambangan, Pengg. |
6.3800 |
6 | ||||||||
|
6 |
Peternakan, Perikanan : Pertambangan, Pengg. |
5.4800 |
5 | ||||||||
|
Subsektor Sekunder | |||||||||||
|
7 |
Industri Pengolahan : Listrik, Gas, Air |
5.7900 |
6 | ||||||||
|
8 |
Industri Pengolahan : Konstruksi |
3.0273 |
3 | ||||||||
|
9 |
Listrik, Gas, Air : Konstruksi |
0.3223 |
1/3 | ||||||||
|
Subsektor Tersier | |||||||||||
|
10 |
Perd., Hotel, Rest : Pengangkutan, Kom. |
7.0950 |
7 | ||||||||
|
11 |
Perd., Hotel, Rest : Keu., Persewaan, Jasa Per. |
7.0067 |
7 | ||||||||
|
12 |
Perd., Hotel, Rest : Jasa-Jasa |
6.1862 |
6 | ||||||||
|
13 |
Pengangkutan, Kom. : Keu., Persewaan, Jasa Per. |
2.6566 |
3 | ||||||||
|
14 |
Pengangkutan, Kom. : Jasa-Jasa |
1.3164 |
1 | ||||||||
|
15 |
Keu., Persewaan, Jasa Per. : Jasa-Jasa |
1.4383 |
1 | ||||||||
|
Dengan mengambil bobot AHP pada Tabel 6 disusun matriks perbandingan berpasangan sebagai berikut PST a= 1 3 1/2 = [1/3 1 1/4] T 241 SP 1 SP 2 SP 3 b=1 136 = 2 [1/3 1 5] SP3 1/6 1/5 1 SS 1 SS 2 SS 3 C-SS1 163 = 2 [1/6 1 1/3] SS3 1/3 3 1 ST 1 ST2 ST3 ST4 ST1 1 7 76 D= 2 1/7 1 3 1 ST3 1/7 1/3 1 1 ST4 1/6 1 1 1 Masing-masing matriks diuji | |||||||||||
|
P |
S |
T | |||||||||
|
P |
1.0000 |
3.0000 |
0.5000 | ||||||||
|
S |
0.3333 |
1.0000 |
0.2500 | ||||||||
|
T |
2.0000 |
4.0000 |
1.0000 | ||||||||
|
Jumlah |
3.3333 |
8.0000 |
1.7500 | ||||||||
|
Langkah 2: menormalkan matriks dengan cara membagi elemen dengan jumlahan di masing-masing kolom. Hasil ditunjukkan oleh Tabel 7. Langkah 3: menjumlahkan elemen dalam satu baris, kemudian membaginya dengan banyak kriteria dari matriks A(n=3). Hasil ini merupakan vektor prioritas dari matriks tersebut. Tabel 7. Perhitungan Vektor Prioritas | |||||||||||
|
konsistensinya menggunakan persamaan (2). Sebelumnya akan dicari terlebih dahulu nilai ^maksimum dari masing-masing matriks. Adapun langkah-langkahnya sebagai berikut (Parapat [4]): Langkah 1: menjumlahkan elemen dalam satu kolom. PST a= 1 3 1/2 = [1/3 1 1/4] T 241 |
P |
S |
T |
Jumlah |
Vektor Prioritas | ||||||
|
P |
0.3000 |
0.3750 |
0.2857 |
0.9607 |
0.3202 | ||||||
|
S |
0.1000 |
0.1250 |
0.1429 |
0.3679 |
0.1226 | ||||||
|
T |
0.6000 |
0.5000 |
0.5714 |
1.6714 |
0.5571 | ||||||
|
Langkah 4: Berikutnya ^maksimum dicari menggunakan persamaan = λx . Nilai X adalah vektor prioritas yang diperoleh pada penghitungan | |||||||||||
Langkah 3.
Pertama dihitung nilai Ax diperoleh
1.0000 3.0000
Ax = [0.3333 1.0000
2.0000 4.0000
=
0.9667
0.3687
1.6881
0.5000
0.2500
1.0000
][0.3202
0.1226
0.5571
… (a)
Selanjutnya dihitung λx diperoleh
λx =
0.3202
0.1226
0.5571
Kemudian Ax =
0.9667 0.3202
[0.3687] = Λ [0.1226]
1.6881 0.5571
0.3202 0.9667
λ [0.1226] = [0.3687]
0.5571 1.6881
Nilai ^■maksimum diperoleh dengan membagi hasil (a) dengan vektor prioritas. Hasil tersebut selanjutnya dijumlahkan dan dibagi dengan banyak kriteria (n)
0.9667 0.3202 0.9667/0.3202
λ=[0.3687]:[0.1226] =[0.3687/0.1226]
1.6881 0.5571 1.6881/0.5571
3.0186 [3.0065
3.0299
Berdasarkan uji konsistensi diketahui bahwa matriks A,B,C dan D konsisten. Langkah berikutnya matriks yang berbobot skala AHP diubah ke dalam skala triangular fuzzy number (TFN). Adapun skala TFN yg digunakan adalah skala pada Tabel 3, sehingga diperoleh
=
3.0186 + 3.0065 + 3.0299
3
3.0183
Berikutnya, dihitung nilai indeks konsistensi
( CI) dengan persamaan (1) sehingga diperoleh
^max -n n-1
3.0183 - 3
3-1
= 0.0092
Berdasarkan Tabel 2, untuk n=3 maka
RI = 0.52, sehingga
Berikutnya dilakukan proses synthetic dengan langkah-langkah sebagai berikut:
1) Menghitung nilai fuzzy synthetic extent
Pertama akan dihitung ∑j=l^gi, yaitu dengan menjumlahkan tiap-tiap bilangan fuzzy dalam setiap baris.
Matriks A
CI
RI
0.0092
0.52
= 0.0176
Untuk matriks A diperoleh CR < 0.1000, hal ini berarti penilaian yang diperoleh dari responden adalah konsisten.
Pada matriks B,C dan D dilakukan pengujian konsistensi dengan langkah dan proses yang sama. Hasil pengujian terdapat pada Tabel 8.
|
P |
S |
T |
Ʃ | |||||||||
|
l |
m |
u |
1 |
m |
u |
1 |
m |
u |
Ʃ1 \ |
Ʃm |
Ʃu I | |
|
P |
1 |
1 |
1 |
2 |
3 |
4 |
1 3 |
1 2 |
1 |
10 3 |
9 2 |
6 |
|
S |
1 4 |
1 3 |
1 2 |
1 |
1 |
1 |
1 5 |
1 4 |
1 3 |
29 20 |
19 12 |
11 6 |
|
T |
1 |
2 |
3 |
3 |
4 |
5 |
1 |
1 |
1 |
5 |
7 |
9 |
Tabel 8. Hasil Uji Konsistensi
|
Matriks |
^max |
CI |
CR |
Keterangan |
|
B |
3.0952 |
0.0476 |
0.0915 |
Konsisten |
|
C |
3.0183 |
0.0092 |
0.0176 |
Konsisten |
|
D |
4.1623 |
0.0541 |
0.0608 |
Konsisten |
Kemudian menghitung nilai [∑F=i ∑ T=I M9i ] dengan menjumlahkan keseluruhan tiap-tiap bilangan fuzzy pada baris dan kolom.
|
Ʃ1 \ |
Ʃm \ |
Ʃu I | |
|
P |
3.3333 |
4.5000 |
6.0000 |
|
S |
1.4500 |
1.5833 |
1.8333 |
|
T |
5.0000 |
7.0000 |
9.0000 |
|
ƩƩ |
9.7833 |
13.0833 |
16.8333 |
|
⎡ (1,1,1) |
(2,3,4) |
(13,12,1)⎤ | ||
|
a=⎢⎢⎢ |
111 (4,3,2) |
(1,1,1) |
(15,14,13)⎥⎥ | |
|
⎣ (1,2,3) |
(3,4,5) |
(1,1,1) ⎦ | ||
|
(1,1,1) |
(2,3,4) |
(5,6,7) | ||
|
= |
⎢⎢⎡(14,13,12) |
(1,1,1) |
(4,5,6) |
⎥⎥ |
|
⎢111 ⎣(7,6,5) |
111 (6,5,4) |
(1,1,1)⎦ |
⎥ | |
|
(1,1,1) |
(5,6,7) |
(2,3,4) | ||
|
c= |
⎢⎢⎡(17,16,15) |
(1,1,1) |
111 (4,3,2) |
⎥⎥ |
|
⎣⎢(14,13,12) |
(2,3,4) |
(1,1,1) ⎦ |
⎥ | |
|
(1,1,1) |
(6,7,8) |
(6,7,8) |
(5,6,7) | |
|
⎢111 ⎢(8,7,6) |
(1,1,1) 111 |
(2,3,4) |
(1,1,1)⎥⎥ | |
|
D= |
⎢111 ⎢(8,7,6) |
(4,3,2) |
(1,1,1) |
(1,1,1)⎥ |
|
⎢111 ⎣(7,6,5) |
(1,1,1) |
(1,1,1) |
(1,1,1)⎦⎥ |
Sehingga diperoleh nilai [∑F=ι ∑ 7=1 M9t ]
adalah (
111
16.8333 , 13.0833 ,9.7833
).
Menggunakan persamaan (3) dihitung nilai fuzzy synthetic extent, diperoleh
Si=(3.3333,4.5000, 6.0000)
111
⊗(16.8333, 13.0833,9.7833)
=(0.1980, 0.3439,0.6133)
S2 =(1.4500, 1.5833,1.8333)
⊗(
111
16.8333, 13.0833, 9.7833
=(0.0861,0.1210, 0.1874)
S3 =(5.0000, 7.0000,9.0000)
⊗(
111
16.8333, 13.0833, 9.7833
=(0.2970,0.5350, 0.9199)
-
2) Menghitung tingkat kemungkinan fuzzy synthetic.
Dari nilai fuzzy synthetic yang telah dihitung pada langkah sebelumnya, maka diperoleh perbandingan tingkat kemungkinan
V(Si ≥ S2) = 1.0000
V(Si ≥ S3 )
0.2970 - 0.6133
= (0.3439 - 0.6133) - (0.5350 - 0.2970)
= 0.6234
V(S2 ≥ Si) = 0.0000
V(S2 ≥ S3) = 0.0000
V(S3 ≥ Si) = 1.0000
V(S3 ≥ S2) = 1.0000
Setelah nilai fuzzy synthetic
dibandingkan, selanjutnya diambil nilai minimumnya. Menggunakan persamaan (7) diperoleh
d' (P)=minV( Si ≥ S2 , S3 )
=min(1.0000, 0.6234)
= 0.6234
d' (S)=minV(S2 ≥ Si , S3 )
=min(0.0000, 0.0000)
= 0.0000
d' (T)=minV( S3 ≥ Si , S2 )
=min(1.0000,1.0000)
= 1.0000
-
3) Menormalisasi vektor bobot.
Diperoleh vektor bobot untuk matriks A dalam bilangan fuzzy
W’ (A)=(d’ (P), d’ (S), d’ (T)) T
W’ (A) =(0.6234, 0.0000, 1.0000 )T
Selanjutnya vektor bobot dinormalisasi menggunakan persamaan (9), diperoleh
0.6234
d(P) = 0.6234 + 0.0000 + 1.0000 = 0.3840
0.0000
d(S) = 0.6234 + 0.0000 + 1.0000 = 0.0000
1.0000
d(T ) = 0.6234 + 0.0000 + 1.0000 = 0.6160 Jadi vektor bobot untuk matriks A adalah W(A)=(0.3840,0.0000,0.6160)T.
Langkah dan proses yang sama dilakukan pada matriks B,C dan D untuk memperoleh vektor bobot. Hasil penghitungan adalah sebagai berikut
|
Matriks B | |||
|
d(SP1) |
d(SP2) |
d(SP3) | |
|
W(B) |
0.7187 |
0.2813 |
0.0000 |
|
Matriks C | |||
|
d(SS1) |
d(SS2) |
d(SS3) | |
|
W(C) |
0.9535 |
0.0000 |
0.0465 |
Matriks D
|
d(ST1) |
d(ST2) |
d(ST3) |
d(ST4) | |
|
W(D) |
1.0000 |
0.0000 |
0.0000 |
0.0000 |
Selanjutnya hasil ini dicocokan dengan data ekonomi Provinsi Bali yang ada, yaitu data Produk Domestik Regional Bruto (PDRB) Tahun 2013.
Tabel 9. Data PDRB Tahun 2013
|
Sektor |
Share* |
|
Primer |
6417.93 |
|
Sekunder |
5543.20 |
|
Tersier |
22826 |
|
PDRB |
34787.96 |
|
Pertanian dan Kehutanan |
3210.03 |
|
Peternakan dan Perikanan |
2945.49 |
|
Pertambangan dan Penggalian |
262.41 |
|
Industri Pengolahan |
3437.55 |
|
Listrik, Gas dan Air Bersih |
557.47 |
|
Konstruksi |
1558.18 |
|
Perdagangan, Hotel dan Restoran |
11181.37 |
|
Pengangkutan dan Komunikasi |
3854.63 |
|
Keuangan, Persewaan dan Jasa Perusahaan |
2544.37 |
|
Jasa-jasa |
5246.46 |
Sumber : Bali Dalam Angka (2014)
Keterangan : *Share dalam miliar rupiah
Dari hasil pencocokan antara hasil perhitungan Fuzzy AHP dengan data PDRB Provinsi Bali diketahui bahwa terdapat kesamaan pada komponen yang paling dominan dari masing-masing kelompok. Hasil yang diperoleh tersebut menyatakan bahwa terdapat kesamaan informasi antara data yang diperoleh melalui persepsi dan data distribusi PDRB Provinsi Bali Tahun 2013.
Data PDRB Provinsi Bali Tahun 2013 menunjukkan bahwa pada kelompok sektor komponen yang memiliki distribusi tertinggi adalah sektor tersier dengan distribusi sebesar 22826 miliar, hal serupa terjadi pada hasil hitung menggunakan metode fuzzy AHP, diperoleh tingkat dominan sektor tersier (T) sebesar 0.6160.
Pada kelompok subsektor, data PDRB menunjukkan bahwa komponen sub tersier yaitu perdagangan, hotel, dan restoran adalah komponen yang paling dominan di kelompoknya, hal serupa terjadi pada penghitungan fuzzy AHP, diperoleh tingkat dominan perdagangan, hotel, dan restoran (ST1) sebesar 1.0000.
Pada kelompok sub sekunder, data PDRB menunjukkan bahwa industri pengolahan adalah komponen yang paling dominan di kelompoknya, hal serupa terjadi pada penghitungan fuzzy AHP, diperoleh tingkat dominan industri pengolahan (SS1) sebesar 0.9535. Pada kelompok sub primer, data PDRB menunjukkan bahwa pertanian dan kehutanan adalah komponen yang paling dominan di kelompoknya, hal serupa terjadi pada penghitungan fuzzy AHP, diperoleh tingkat dominan pertanian dan kehutanan (SP1) sebesar 0.7187. Hal ini berarti persepsi yang diberikan sesuai dengan kondisi ekonomi yang terjadi di Provinsi Bali.
Pada penelitian ini dapat disimpulkan bahwa dengan menerapkan metode Fuzzy Analytic Hierarchy Process diperoleh hasil bahwa menurut aktivitasnya komponen yang berkontribusi dominan pada perekonomian Provinsi Bali adalah sektor tersier. Pada
kelompok subsektor primer komponen yang berkontribusi dominan adalah pertanian dan kehutanan. Pada kelompok subsektor sekunder komponen yang berkontribusi dominan adalah industri pengolahan. Pada kelompok subsektor tersier komponen yang berkontribusi dominan adalah perdagangan, hotel, dan restoran.
Saran yang dapat diberikan kepada peneliti yang akan menerapkan metode fuzzy AHP adalah mencoba untuk mengurangi selang skala penilaian dan menggunakan skala triangular fuzzy number dengan beda I, m, dan u yaitu 0.5. Hal ini bertujuan untuk memperoleh nilai vektor prioritas yang lebih besar dari nol. Hasil nol yang diperoleh pada penelitian ini kemungkinan disebabkan oleh interval nilai yang cukup jauh antara variabel yang dibandingkan. Interval yang cukup jauh akan mengakibatkan jarak yang jauh pada nilai fuzzy synthetic. Dampaknya adalah ketika membandingkan dua nilai synthetic, antara nilai synthetic tidak beririsan sehingga tidak terdapat nilai perpotongan ( d). Akibatnya, perbandingan nilai synthetic bernilai nol.
DAFTAR PUSTAKA
-
[1] BPS, 2014. Bali Dalam Angka 2014.
Denpasar: BPS Provinsi Bali.
-
[2] Chang, Da-Yong, 1996. Applications of the Extent Analysis Method on Fuzzy AHP. European Journal Of Operational Research, pp. 649-655.
-
[3] Hsu, Yu-Lung, Lee, Cheng-Haw. & V.B.
Kreng, 2010. The application of Fuzzy Delphi Method and Fuzzy AHP in lubricant regenerative technologi selection. Expert System with Application, pp. 419-425
-
[4] Parapat, D. J., 2009. Model Penentuan Prioritas Dalam AHP Melalui Koefisien Korelasi, Thesis. Medan: Pascasarjana Universitas Sumatera Utara.
-
[5] Saaty, T. L. & Kearns, K. P., 1985.
Analytical Planning The Organization of Systems. Pergamon Press
-
[6] Saaty, T. L. & Vargas, L. G., 2001.
Models, Methods, Concepts & Applications of the Analytic Hierarchy Process. New York: Springer Science + Business Media.
66
Discussion and feedback