ANALISIS MODEL REGRESI NONPARAMETRIK SIRKULAR-LINEAR BERGANDA
on
E-Jurnal Matematika Vol. 5 (2), Mei 2016, pp. 52-58
ISSN: 2303-1751
ANALISIS MODEL REGRESI NONPARAMETRIK SIRKULAR-LINEAR BERGANDA
Komang Candra Ivan§1, I Wayan Sumarjaya2, Made Susilawati3
1Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: candraivankomang@gmail.com]
-
2Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: sumarjaya@gmail.com] 3Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: susilawati.made@gmail.com]
§Corresponding Author
ABSTRACT
Circular data are data which the value in form of vector is circular data. Statistic analysis that is used in analyzing circular data is circular statistics analysis. In regression analysis, if any of predictor or response variables or both are circular then the regression analysis used is called circular regression analysis. Observation data in circular statistic which use direction and time units usually don’t satisfy all of the parametric assumptions, thus making nonparametric regression as a good solution. Nonparametric regression function estimation is using epanechnikov kernel estimator for the linier variables and von Mises kernel estimator for the circular variable. This study showed that the result of circular analysis by using circular descriptive statistic is better than common statistic. Multiple circular-linier nonparametric regressions with Epanechnikov and von Mises kernel estimator didn’t create estimation model explicitly as parametric regression does, but create estimation from its observation knots instead.
Keywords: Circular Data, Circular Regression, Circular-Linier Nonparametric Regression
Dalam beberapa kasus penelitian, peneliti terkadang harus melakukan pengukuran terhadap data yang bersatuan waktu atau derajat arah yang nilai-nilainya berulang secara periodik. Sebagai contoh penelitian tentang arah migrasi hewan menghasilkan data pengamatan yang bersatuan arah. Kumpulan data pengamatan yang bersatuan arah disebut data berarah. Jika penelitian arah migrasi hewan dilakukan pada jarak migrasi tertentu, maka data pengamatan memiliki besaran vektor. Jika pengamatan tersebut digambarkan dalam besaran vektor, maka data pengamatan disebut data sirkular (Jammalamadaka & SenGupta[1]).
Data sirkular tidak memiliki nilai minimum dan maksimum dan data awalnya sama dengan data terakhir yaitu data pada arah 0 radian sama dengan data pada arah 2pπ radian untuk P bilangan bulat positif. Analisis statistika yang digunakan untuk menganalisis data sirkular adalah analisis statistika sirkular.
Dalam analisis regresi, jika salah satu atau keduanya dari variabel prediktor atau variabel respons adalah data sirkular, maka analisis regresi yang digunakan disebut analisis regresi sirkular.
Data pengamatan pada statistika sirkular yang bersatuan arah atau waktu memiliki kecenderungan tidak memenuhi asumsi-asumsi yang mendasari uji parametrik terutama sisaan harus berdistribusi normal. Regresi nonparametrik bisa menjadi alternatif dalam penelitian, karena penggunaan uji nonparametrik berlandaskan asumsi yang umum dan tidak memperhatikan asumsi kenormalan galat. Estimasi fungsi dalam regresi nonparametrik menggunakan teknik smoothing. Estimator kernel adalah salah satu teknik smoothing yang paling umum digunakan (Wand & Jones [7]).
Penelitian ini membahas penggunaan regresi nonparametrik sirkular-linear berganda antara variabel respons linear dengan variabel prediktor sirkular dan linear.
Data sirkular adalah data yang nilai-nilainya berulang secara periodik dengan responnya bukan skalar tetapi angular atau berarah sehingga dikategorikan sebagai data berarah (Jammalamadaka & SenGupta [1]). Pengukuran data sirkular biasanya dalam satuan derajat 0 sampai 360 atau dalam satuan radian dari 0 radian sampai 2 radian.
Menentukan arah rata-rata untuk data sirkular dilakukan dengan memperlakukan data sirkular dalam vektor unit dan
Menurut Mardia dalam Nurhab [2] mendefinisikan ragam sampel sirkular adalah
=1- =1- ̅
n
dengan adalah panjang vektor resultan
=‖ ‖=√ + ,0≤ ≤1.
dan adalah panjang rata-rata dari vektor resultan dengan 0≤ ̅≤1. Nilai ragam yang semakin kecil menandakan data semakin
menggunakan arah dari vektor resultannya (Jammalamadaka & SenGupta [1]). Arah rata-rata sirkular ( ) diperoleh dari
(
arctan
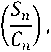
π
2,
Cn >0 , Sn ≥ 0
Cn = 0, Sn >0
^^^^I θ =
arctan I — ' Cn
+ π,
V
arctan I — ' Cn
+ 2π,
tidak terdefinisi,
Cn <0
Cn ≥ 0 , Sn <0
Cn = 0 , Sn = 0
dengan(Cn, Sn) adalah fungsi cosinus dan
fungsi sinus yang diperoleh dari
Cn = ∑F=ιcosθt, i = 1,2,...,n
Sn = ∑y=ιsinθi,i = 1,2,...,n
Median data sirkular menurut Mardia
dalam Otieno [3] menyatakan bahwa median sampel θ dari data sampel sirkular θi, θ2,..., θn adalah titik P pada keliling lingkaran yang memiliki sifat:
-
1. Diameter PQ dengan Q adalah anti-median membagi lingkaran menjadi dua bagian, yang setiap bagiannya memiliki jumlah pengamatan sama banyak.
-
2. Sebagian besar data pengamatan berada disekitar titik P dibandingkan di titik Q.
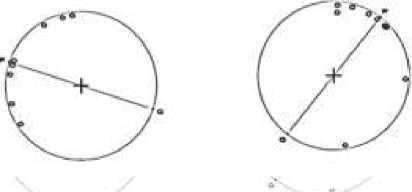
Gambar 1. Median Sirkular untuk Data Genap dan
Data Ganjil
terkonsentrasi menuju suatu titik tertentu.
Regresi sirkular-linear yaitu analisis regresi dengan variabel prediktor sirkular dan variabel responnya linear. Menurut SenGupta dan Ugwuowo [5], model regresi sirkular linear antara variabel respons linear Y dan variabel prediktor sirkular θ adalah
Yi = β0 + Ai cos ω(θ — θ0) + £j
dengan β0 dan Ai adalah parameter yang belum diketahui nilainya, θ0 adalah sebuah acrophase, dan ^i adalah komponen galat acak. Sedangkan, ω adalah frekuensi angular.
Statistika nonparametrik adalah statistika bebas sebaran yang digunakan dengan mengabaikan asumsi-asumsi yang harus dipenuhi pada statistika parametrik. Dalam statistika nonparametrik bentuk kurva yang kurang mulus dapat dipermulus dengan menggunakan teknik smoothing. Salah satu teknik smoothing yang umum digunakan adalah estimator kernel K(C) pada pemanfaatannya dilakukan pada setiap titik data (Sukarsa & Srinadi [6]).
Estimator kernel merupakan pengembangan dari estimator histogram. Salah satu fungsi kernel yaitu kernel epanechnikov yang memiliki bentuk
K(%)=⅛-%2)∕(∣%∣≤1)
4
dengan T4 adalah fungsi indikator untuk suatu himpunan A yaitu
Ta(x) =
(i ,x∈a ,0,x∉a
Kernel von Mises adalah kernel sirkular orde kedua (second-order circular kernel) yang memiliki bentuk
κκ (θ)= ( ) exp[ κ cos(θ)],0≤θ
( )
dengan θ adalah variabel prediktor sirkular, K adalah parameter konsentrasi (concentration parameter) dan Iq (K) adalah fungsi Bessel termodifikasi orde nol,
Iq (k)=⅛ ∫ ехр[κ cos(Φ)] d φ.
Parameter Bandwidth disebut juga parameter pemulusan (smoothing) yang memiliki peran seperti lebar interval pada histogram. Parameter bandwidth akan mengontrol kemulusan kurva regresi yang diestimasi. Metode yang dapat digunakan yaitu metode Cross-Validation (CV) yang didefinisikan sebagai berikut
CV(ℎ Q,…,ℎ2, *1 ,…,K2)=∑F=I( Yt - ̂ -i (ιi))2
dengan ̂ -i (k ) adalah penduga leave-one-out dengan menghilangkan k.
Bentuk umum model regresi sirkular-linear berganda adalah (SengGupta & Ugwuowo [4])
Yi = +∑KiPlXl +A cos ω(θi - θo)+εi
dengan Yi adalah variabel respons linear, M adalah nilai rataan, β adalah koefisien regresi, ^i adalah variabel prediktor linear, A adalah amplitudo, ω adalah frekuensi angular, Pi adalah variabel prediktor sirkular yang menentukan periode T, Θq adalah acrophase dan εi adalah komponen galat acak.
Kemudian Qin [4] mengasumsikan bentuk model regresi nonparametrik sirkular-linear berganda dengan bentuk
Yi = ( Li)+εi ,i=1,2,…․,n
dengan Yi adalah variabel respons skalar, m(Li ) adalah fungsi regresi, (Li)=(xiT,ΘiT)T, xiT dan Θ i masing-masing adalah d1 dimensi linear dan ^2 dimensi sirkular, serta εi adalah variabel acak berdistribusi IID (Independent
and Identically Distributed) dengan rataan nol
dan ragam unit dan bebas dari Li .
Misalkan y=(Yi , Y2,…,Yn )
sebagai
vektor variabel respons,
=
1
1
( Xl -X) τ sin(Θ 1-Θ)T
( Xn -x) τ sin(Θ n -Θ)T
sebagai desain matriks, dan
Wi = {Khc (Li -l),…,Khc (Ln -l)}
sebagai bobot matriks, dengan l adalah sampel acak dari fungsi densitas peluang bersama f(I)=fx (x) fe (θ ) dan Khc adalah fungsi linear–sirkular
K∏c (Li -l)=Kh (Xi -x)․ Kc (Θ i-θ)
=√K… ∏ICK( )(ℎ (⅞ -
xi))․∏P = I Kκp (Θip - θv ) dengan K( hJ) adalah kernel linear standar dan
Kjcp adalah kernel sirkular orde kedua. Penduga kernel kuadrat terkecil linear lokal dari m(l) diperoleh dari masukan pertama dari vektor
̂ =argmina ,β∑i=i{ Yi -a- Pt (Li -
l)}2 Khc (Li -l)
=(L1tW1L1) 1LlτWly.
Dengan demikian penduga kernel kuadrat terkecil linear lokal dari m(l ) adalah ̂(l;H,C)=eιτ (L1tW1L1) 1LlrWly dengan eι adalah vektor berukuran (d1 + ^2 + 1) × 1 dengan nilai 1 pada masukan pertama dan yang lainnya 0.
Vektor dari nilai yang diduga (fitted values) ̂=( ̂(Li),…,( ̂(K)) adalah ̂=L(LitW1L1)~1LlτWly
Jenis data yang digunakan dalam penelitian ini adalah data sekunder. Data sekunder ini berupa data per hari curah hujan, data per hari temperatur maksmimum, data per hari temperatur minimum, data per hari kecepatan angin, dan data per hari arah angin pada tahun 2006–2010 yang diperoleh dari National Climatic Data Center–National
Oceanic and Atmospheric Administration (NCDC-NOAA) Amerika Serikat yang diunduh dari http://www.ncdc.noaa.gov.
Data yang diperoleh dalam penelitian ini dianalisis menggunakan metode regresi nonparametrik sirkular-linear berganda dengan bantuan software R dan software MATLAB R2009a. Langkah-langkah yang dilakukan untuk mencapai tujuan penelitian ini adalah sebagai berikut:
-
1. Membuat analisis deskriptif statistika untuk masing-masing peubah bebas.
-
a) Representasi grafis data linear dengan histogram dan grafis data sirkular dengan diagram pancar.
-
b) Menghitung ukuran pemusatan data untuk masing-masing peubah linear dan peubah sirkular.
-
c) Menghitung keragaman data untuk
masing-masing peubah linear dan
peubah sirkular.
-
2. Melakukan analisis regresi nonparametrik sirkular-linear berganda, yaitu dengan membangun model
Yi = m(Lj) + εi ,i = 1,2, .„,n
-
3. Mengestimasi kurva regresi nonparametrik dengan estimator kernel. Estimasi kernel variabel linear menggunakan estimasi segitiga (triangle), dan estimasi kernel variabel sirkular menggunakan estimasi von Mises.
-
4. Interpretasi kurva regresi nonparametrik
Gambaran umum data yang diolah menggunakan software R dapat dilihat pada tabel 1. Hasil analisis deskripif variabel sirkular arah angin dengan menggunakan statistika deskriptif secara umum, menghasilkan arah angin minimum yaitu 0,17 radians, arah angin maksimum yaitu 6,28 radians, median arah angin yaitu 3,66 radians, rata-rata arah angin yaitu 3,46 radians, dan keragaman data arah angin yaitu 3,09.
Tabel 1. Statistika Deskriptif Data Curah Hujan, Data Temperatur Maksimum, Data Temperatur Minimum, Data Kecepatan Angin, dan Data Arah Angin.
|
Variabel |
Ringkasan Statistik | ||||||
|
Min |
Maks |
Median |
Rata-rata |
Varians |
Skewness |
Kurtosis | |
|
Curah Hujan (mm) |
0,00 |
152,90 |
0,00 |
2,42 |
53,43 |
8,0127 |
119,597 |
|
Temperatur Maksimum (0C) |
-18,80 |
36,70 |
16,70 |
15,33 |
141,61 |
-0,3605 |
2,03832 |
|
Temperatur Minimum (0C) |
-29,90 |
25,60 |
5,00 |
4,461 |
112,60 |
-0,3368 |
2,35443 |
|
Kecepatan Angin (mps) |
0,20 |
12,20 |
3,70 |
3,940 |
3,15 |
2,3544 |
0,722019 |
|
Arah Angin (radians) |
0,17 |
6,28 |
3,66 |
3,46 |
3,09 | ||
Hasil analisis deskriptif variabel sirkular arah angin dengan menggunakan statistika sirkular dapat dilihat pada tabel berikut.
Tabel 2. Statistika Deskriptif Data Arah Angin.
|
Variabel |
N |
Min |
Maks |
Median |
Mean |
Varians |
|
Arah Angin |
1812 |
0,17 |
6,28 |
1,57 |
1,44 |
0,84 |
adalah 0.84. Keragaman yang dihasilkan lebih kecil yang berarti semakin baik. Perbedaan kedua hasil penghitungan median dan rata-rata data arah angin akan lebih mudah dideskripsikan dengan bantuan grafik. Plot data arah angin dapat dilihat pada Gambar 2.
Dengan statistika sirkular, menghasilkan perbedaan nilai median data arah angin adalah 1,57 radians, rata-rata data arah angin adalah 1,44 radians, dan keragaman data arah angin
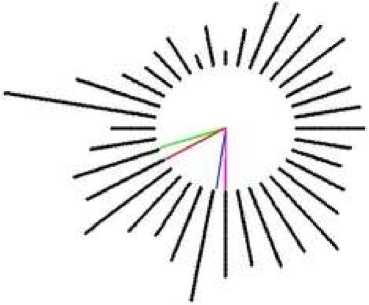
Gambar 2. Plot Data Sirkular
Arah rata-rata dan median arah angin yang dihitung dengan menggunakan statistika secara umum masing-masing ditunjukkan oleh garis hijau untuk arah rata-rata (3,46 radians) dan garis cyan untuk median (3,66 radians). Sedangkan, arah rata-rata dan median arah angin yang dihitung dengan menggunakan statistika sirkular masing-masing ditunjukkan oleh garis biru untuk arah rata-rata (4,58 radians) dan garis ungu untuk median (4,71 radians). Jika dilihat dari bentuk diagram pencar, maka plot data arah angin tersebut lebih terkonsentrasi ke arah Selatan atau ke arah 4,58. Radians dan 4,71 radians.
Pendugaan fungsi nonparametrik m(Li ) menggunakan estimator kernel yaitu dengan estimasi kernel Epanechnikov untuk variabel temperatur maksimum, temperatur minimum, kecepatan angin, dan estimasi kernel von Mises untuk variabel sirkular. . Untuk memperoleh estimasi fungsi nonparametrik yang optimal, dilakukan pendugaan kurva regresi nonparametrik dengan bandwidth yang optimal. Pemilihan bandwidth yang optimal ditentukan berdasarkan kriteria nilai CV yang minimum.
Nilai bandwidth yang optimal untuk masing-masing variabel dapat dilihat pada tabel 3.
Tabel 3. Nilai Bandwidth untuk Masing-masing Variabel.
|
Variabel |
Kernel |
Bandwidth |
|
Temperatur Maksimum |
Epanechnikov |
8,381633 |
|
Temperatur Minimum |
Epanechnikov |
13,98827 |
|
Kecepatan Angin |
Epanechnikov |
0,6 |
|
Arah Angin |
von Mises |
6,422491 |
Setelah diperoleh nilai bandwidth yang optimal untuk masing-masing variabel berdasarkan kriteria CV minimum, kemudian dilakukan estimasi model regresi nonparametrik dengan estimator kernel Epanechnikov dan estimator kernel von Mises, yaitu menghitung ̂(I;H,C). Fungsi linear-sirkular K H C(Li -I) yaitu
Khc (Li -I) =0,0503*1
- (0,35(Klι - *ι))2+
×*1-(0,27(Xi2 - *2))2+ ×*1-(1,29( ⅞ - ^3 ))2+ ×I[|0,35(Xil - Xi)|≤1] ×I[|0,27(Xi2 - X2)|≤1] ×I[|1,29(Xi3 - X3)|≤1] × exp[6,42cos(Θa- θι)]
Selanjutnya, dengan bantuan software MATLAB R2009a diperoleh nilai dugaan untuk masing-masing parameter yaitu
̂
⎛ ̂ ⎞
⎜ ̂ ⎟
⎝ ̂̂ ⎠
2․5487
⎛-0․6575⎞ 0․7733
3․5731 ⎝-0․3067⎠
Dengan demikian, pendugaan kernel
kuadrat terkecil linear lokal dari m(I) adalah
̂(I;H,C)=eι (LlτWlLl) ∖τWly
=(1 0 0 0 0)
2․5487
⎛-0․6575⎞ 0․7733
= 2․5487.
3․5731 ⎝-0․3067⎠
Plot nilai y dan ̂ terhadap hari dapat dilihat pada gambar berikut.
1α1-1-------i—--—r—
ICC ■
S ■
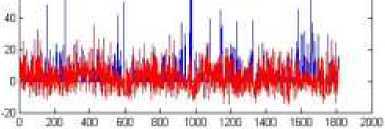
Gambar 3. Plot y dan ̂ Terhadap Hari Untuk Semua Data Amatan
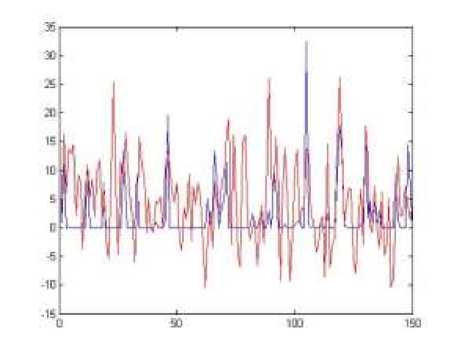
Gambar 4. Plot y dan ̂ Terhadap Hari Untuk 150 Data Amatan Pertama
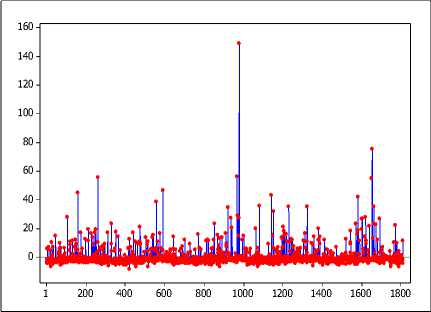
Gambar 5. Plot Residual Terhadap Hari Untuk Semua Data Amatan
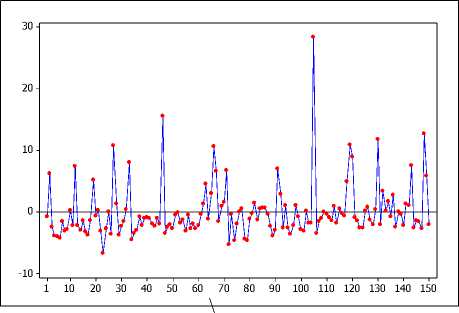
Gambar 6. Plot Residual Terhadap Hari Untuk 150
Amatan Pertama
Pada Gambar 3 dan Gambar 4, plot y ditunjukkan oleh garis warna biru, sedangkan plot ̂ ditunjukkan oleh garis merah. Plot y dan ̂ menunjukkan banyak nilai ̂ yang tidak sesuai dengan nilai y sebenarnya yang mengindikasikan estimasi model yang diperoleh kurang baik. Plot sisaan (residual) pada Gambar 5 dan Gambar 6 menunjukkan banyak nilai sisaan yang berada jauh dari garis sisaan = 0.
Penghitungan dengan statistika sirkular menghasilkan arah rata-rata dan median data sirkular masing-masing yaitu 4,58 radians dan 4,71 radians, sedangkan penghitungan dengan statistika deskriptif secara umum menghasilkan arah rata-rata dan median masing-masing yaitu 3,46 radians dan 3,66 radians. Jika dilihat dari bentuk diagram pencar, maka plot data arah angin lebih terkonsentrasi ke arah Selatan atau ke arah 4,58 radians dan 4,71 radians.
Regresi nonparametrik sirkular-linear berganda dengan estimator kernel epanechnikov dan von Mises tidak menghasilkan model estimasi secara eksplisit seperti regresi parametrik melainkan estimasi dari titik-titik amatan.
Fungsi kernel linear-sirkular ^HC (Li -l) yang diperoleh adalah sebagai berikut:
Khc (Li -l) = 0,0503
-
* 1 - (0,35(Xii - *1))2+
-
* 1 - (0,27(Xi2 - *2 ))2+
-
* 1 - (1,29(¾ - ^3 ))2+
I[|0,35(Xil - Xi)|≤1]
I[|0,27(Xi2 - *2)|≤1]
I[|1,29(Xi3 - X3)|≤1] ехр[6,423cos(Θil - θl)]
Penanganan terhadap data yang mengandung pencilan (outlier) masih belum dibahas dalam penelitian ini, sehingga penelitian selanjutnya dapat lebih
menyempurnakan dengan menerapkan suatu metode untuk mengatasi pengaruh pencilan. Selain itu, pembahasan regresi sirkular tidak hanya pada regresi sirkular-linear saja, tetapi masih terdapat dua pembahasan yang tidak kalah penting juga yaitu regresi sirkular-sirkular dan regresi linear-sirkular, sehingga penelitian lebih lanjut dapat melakukan pengembangan pada kedua regresi tersebut.
DAFTAR PUSTAKA
-
[1] Jammalamadaka, S. R. dan SenGupta, A. (2001). Topics in Circular Statistics. Singapore : World Scientific Publishing.
-
[2] Nurhab, M. I. (2014). Analisis Regresi Sirkular(2)-Linier Berpangkat m. Tesis Magister. Bogor : Institut Pertanian Bogor.
-
[3] Otieno, B. S. (2002). An Alternative Estimate of Preferred Direction for Circular Data. Dissertation. Virginia
Polytechnic Insitute. Virginia.
-
[4] Qin, Xu. (2011). A Nonparametric Circular-Linear Multivariate Regression Model with Its Application to Wind Energy. International Mathematical Forum, 6, 2615-2624.
-
[5] SenGupta, A. dan Ugwuowo, F. I. (2006). Asymmetric Circular-Linear Multivariate Regression Models with Applications to Environmental Data. Environmental and Ecological Statistics, 13, 299-309.
-
[6] Sukarsa, I.K.G., dan Srinadi, I.G.A.M.. (2012). Estimator Kernel Dalam Model Regresi Nonparametrik. Jurnal
Matematika, 2, 1693-1394.
-
[7] Wand, M.P. dan Jones, M.C. (1995). Kernel Smoothing. New York : Chapman & Hall.
58
Discussion and feedback