PERHITUNGAN NILAI BETA DARI BEBERAPA SAHAM UNGGULAN DI INDONESIA DENGAN MENGGUNAKAN METODE GARCH

E-Jurnal Matematika Vol. 5 (2), Mei 2016, pp. 67-75

ISSN: 2303-1751

PERHITUNGAN NILAI BETA DARI BEBERAPA SAHAM UNGGULAN DI INDONESIA DENGAN MENGGUNAKAN METODE GARCH

Ni Kadek Puspitayanti^§1, Komang Dharmawan², I Putu Eka N. Kencana³

• ¹Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: [email protected]]

• ²Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: [email protected]]

• ³Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: [email protected]] ^§Corresponding Author

ABSTRACT

The objective of investment in the capital market is to acquire dividends and capital gain. The fact proves that the advantage of investation risky assets is uncertain . This is because of the difficulty in analyzing and predicting Return and stock losses due to factors that affect the movement of the stock price , such as economic factors , political , social , and security. The model can be used by investors in predicting stock returns expected that Generalized Autoregressive Conditional Heteroscedaticity (GARCH). In this study calculations beta value of some leading stocks in Indonesia by using Generalized Autoregressive Conditional Heteroscedaticity (GARCH) are presented . The data used this search is secondary data covering daily data sampled 5 shares of PT Unilever Indonesia Tbk , PT Indosat Tbk , PT Indofood Sukses Makmur Tbk , PT Telkom Indonesia Tbk , PT Holcim Indonesia Tbk. From the results described fifth beta value of these shares using the method GARCH beta greater than the market in the period from 23 September 2013 until 24 September 2014.

Keywords: Beta, Capital Gain, Dividen, GARCH, return

• 1.    PENDAHULUAN

Investasi dibedakan menjadi dua yaitu investasi riil (gedung, kendaraan, mesin, tanah) dan investasi finansial (saham pada pasar modal). Tingkat pendapatan yang diharapkan dari investasi saham tergantung dari bagaimana sikap investor dalam menghadapi risiko. Pada umumnya investor bersifat menghindari risiko, walaupun sebagian ada yang berani mengambil risiko. Investor akan mempertimbangkan tingkat penghasilan yang diharapkan (expeted return) atas investasinya untuk periode tertentu pada masa yang akan datang terhadap risiko (risk) yang akan mungkin ditanggung.

Pasar modal menyediakan banyak sekali informasi yang tersedia bagi para investor. Informasi merupakan kebutuhan yang mendasar bagi para investor dalam mengambil keputusan. Seorang investor harus memiliki perencanaan investasi yang efektif agar memperoleh keuntungan di pasar modal. Perencanaan ini meliputi pertimbangan keputusan yang diambil

untuk mengalokasikan dana yang dimiliki dalam bentuk aktiva tertentu dengan harapan mendapat keuntungan ekonomis di masa mendatang. Salah satu bentuk investasi yang dilakukan investor adalah membeli saham, dengan harapan akan memperoleh return baik berupa dividen maupun capital gain.

Dalam pelaksanaan investasi, para pemilik modal (investor) sangat membutuhkan informasi yang jelas, wajar, dan tepat waktu sebagai dasar pertimbangan dalam proses pengambilan keputusan. Salah satu informasi yang dibutuhkan oleh investor (baik investor ritel maupun investor institusional) adalah informasi tentang tingkat pengembalian (return) dan risiko investasi. Metode yang digunakan untuk mengestimasi beta dengan varians adalah metode Generalized Autoregressive Conditional Heteroscedaticity (GARCH). Nilai beta yang telah diperoleh dengan metode GARCH dapat digunakan untuk estimasi sensivitas pengembalian saham beta yang akan

datang sehingga dapat digunakan oleh investor sebagai bahan pertimbangan untuk membuat keputusan investasi.

• 2.    METODE PENELITIAN

Data yang digunakan dalam penelitian ini adalah data sekunder yang bersifat kuantitatif. Data sekunder adalah data yang diambil tidak dari sumber langsung dan merupakan pengumpulan dari pihak lain. Sedangkan data yang bersifat kuantitatif adalah data yang berupa angka yang bisa dihitung atau dioperasikan. Data dalam penelitian ini diakses melalui internet.

• A.    Mencari Tingkat Pengembalian (Return)

Return saham adalah keuntungan yang di peroleh dari kepemilikan saham investasi yang dilakukan. Perhitungan return saham menggunakan metode konvensional sebagai berikut:

R_i, =  ^{, t}- ^- - ^, -             (1)

,t-ι

dengan , adalah return saham i pada periode t,  , adalah indeks saham i pada periode t , dan

, adalah indeks saham i pada periode t-1.

Pada analisis sekuritas umumnya menggunakan metode natural logarithm ratio, dimana hasil dari keuntungan yang diharapkan tidak terlalu besar dibandingkan metode konvensional. Metode natural logarithm ratio di formulasikan sebagai (Husnan [5])

R_i ^,t =ln ( S₁,^,h )                 (2)

Penggunaan metode natural logarithm ratio digunakan agar dalam analisis statistika perhitungan return tidak bisa.

• B.    Fungsi ACF dan PACF

Fungsi autokorelasi digunakan untuk meng ukur ketergantungan bersama (mutual dependen) antara nilai-nilai suatu runtun waktu yang sama pada periode waktu yang berlainan.

^∑t=l ⁽h - ̅)(Zt+k - ̅)

^∑t=l⁽Z_t - ̅) ²

(3)

dengan nilai Pk berkisar antara -1 sampai 1. Untuk fungsi PACF diberikan sebagai berikut

^∅ kk

_P* -∑/=I¹ ∅̂k-l ^, jPk-j

1-∑k-l ∅^̂

• 1-     ∅   ,JpJ

dengan  ∅^̂ k j = ∅^̂k-l,j-∅kk ∅^̂k-l,k-j  untuk

j=1,2,3,…,k-1.

• C.    Uji Ljung Box

Pada Uji Ljung Box akan dilakukan pengujian terhadap data apakah mempunyai unsur autokorelasi atau tidak.

• a.    Menetapkan hipotesis

Hq : data tidak berautokorelasi

Hy : data memiliki autokorelasi

• b.    Menghitung uji statistik Ljung-Box ^m ∕ ^2 \

LB =⁽ⁿ+2)∑( ~_n - ~_k )    (5)

k=i '      '

dengan LB menyatakan statistik Ljung Box, n menyatakan banyaknya data pengamatan, ̂ k merupakan taksiran autokorelasi, dan m adalah panjang lag.

• c.    Daerah penolakan

Kriteria uji dilakukan jika Ho ditolak jika LB >%a _;d f atau p-value < 0.

Apabila Hq ditolak maka akan dipilih Hy yang berarti data berautokorelasi.

• D.    Uji ARCH LM

Uji ARCH LM dilakukan untuk melihat kehadiran unsur heteroscedasticity atau efek GARCH.

• a.    Menetapkan hipotesis

Hq : homoscedasticity, tidak ada efek ARCH-GARCH

Hy : heteroscedasticity, terdapat efek ARCH-GARCH

• b.    Menghitung nilai statistik uji ARCH LM

  U=(n-m)R²         (6)

  
  

R² merupakan koefisien determinasi, n banyaknya data dan m panjang lag.

• c.    Daerah penolakan

Kriteria uji dilakukan apabila tolak H₀ jika >>xa,m atau p-value <α, maka akan dipilih H₁ yang berarti ada efek ARCH-GARCH pada data

• E.    Peramalan dengan model Generalized

Autoregressive Conditional

Heteroskedasticity (GARCH)

Model ARCH pada umumnya digunakan untuk memperkirakan volatilitas yang diperkenalkan oleh Engle pada tahun 1982 di mana ε_t tidak saling berkorelasi. Residual (ε_t) mengikuti model ARCH (q) yang dimodelkan sebagai

^εt — tj_tZt

terhadap perubahan pengembalian pasar. Perhitungan beta sangat penting dilakukan untuk mengetahui berapa besar risiko saham tersebut. Saham dengan nilai β>1 memiliki risiko lebih tinggi dari risiko pasar, sebaliknya saham dengan nilai < 1 memiliki risiko lebih rendah dari risiko pasardan sedangkan saham dengan nilai β=1 menunjukkan bahwa risiko saham sama dengan risiko pasar. Risiko sistematis merupakan risiko yang berasal dari kondisi ekonomi dan kondisi pasar secara umum, dimana risiko ini tercermin dari nilai betanya.

G. Perbandingan Nilai Beta saham Unggulan.

Melakukan perbandingan nilai beta pasar saham unggulan.

^t — ω + β₁⅛ ₁ + - + β_qε_t²- _q

• 3.    HASIL PENELITIAN DAN DISKUSI

q

^σt² = ^ + ∑βi ^t-i i=i

(7)

dengan β₁, ...,βi, dan ω merupakan parameter konstan. Bollerslev mengembangkan model ARCH menjadi model GARCH di mana residual ( ε _t) mengikuti model GARCH (p,q) dengan    merupakan orde ARCH dan

merupakan orde dari GARCH yang dapat dimodelkan sebagai

^εt ^{— σ}t^zt

σ_t² — ω + α₁σ_t²_{- 1} + —+ a_pσ--_p + β₁ε_t²_{- 1} + ••• + ^β q^εt-q

Untuk GARCH  (p, q) variansnya dapat

dirumuskan sebagai berikut:

p             q

σ_t² = ^ω + ∑ ^ai ^σ-~i + ∑ ^^i2t2-i

7=1           1=1

(8)

• A.    Tingkat Pengembalian (Return)

Menentukan nilai return dari data historis penutupan tiap-tiap saham dengan menggunakan metode Metode natural logarithm ratio di formulasikan sebagai (Husnan [5]).

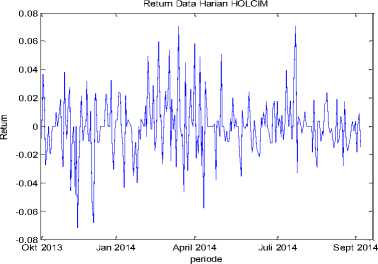
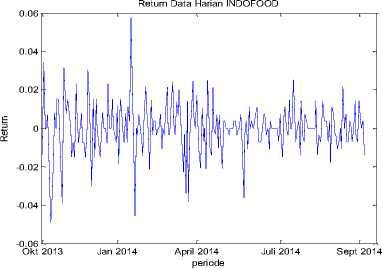
Berikut adalah plot data return tiap-tiap saham

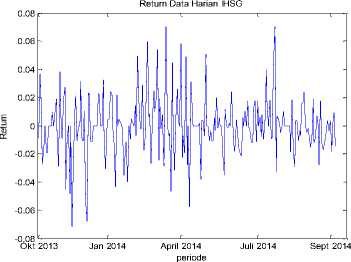
dengan α₁,a ₂ , ...,aj adalah nilai parameter ke i. dari GARCH dan σ_t²_{- 1},σ_t²_{- 2} ,.,σ_t²_{- i} adalah nilai varians ke .

F. Perhitungan Nilai Beta Saham Unggulan

Menghitung Nilai Beta tiap-tiap saham menggunakan GARCH. Beta merupakan ukuran sensitivitas pengembalian saham

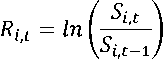
• B.    Generalized Autoregressive Conditional Heteroskedasticity (GARCH)

Penggunaan model GARCH yang digunakan dalam meramalkan model data yang bersifat acak dan volatilitasnya tidak konstan perlu memerhatikan langkah-langkah sebagai berikut, yaitu tahap pra-estimasi dengan melakukan uji terhadap autokorelasi data. Dengan melihat residual kuadratpada data

akan dilihat bahwa data berautokorelasi atau tidak stasioner pada Tabel 3.1

Saham IHSG
Uji Ljung Box Residual Kuadrat p     Qstat   CV 0.8902  0.0191  3.8415 0.4882  4.4382 11.0705 0.5478  7.8649 16.9190 0.6150 10.9504 22.3620 0.4553 16.9866 27.5871 0.2917 24.0278 32.6706	UJI ARCH Residual Kuadrat p     Qstat   CV 0.8893  0.0194  3.8415 0.6545  3.2959 11.0705 0.5554  7.7908 16.9190 0.6177 10.9175 22.3620 0.3708 18.2900 27.5871 0.4755 20.7301 32.6706
Holcim
p     Qstat   CV 0.1474  2.0987  3.8415 0.6533  3.3035  11.0705 0.2409 11.5335 16.9190 0.0489 22.4399 22.3620 0.0270 29.9122 27.5871 0.0249 35.4959 32.6706	p     Qstat   CV 0.1506  2.0660  3.8415 0.6461  3.3509  11.0705 0.1794 12.6440 16.9190 0.1303  18.7741 22.3620 0.1141 24.2014 27.5871 0.1949 26.3086 32.6706
Indofood
p     Qstat   CV 0.0042  8.2058  3.8415 0.0036 17.5508 11.0705 0.0005 29.6503  16.9190 0.0025 31.9264 22.3620 0.0129 32.5277 27.5871 0.0443 33.1801 32.6706	p     Qstat   CV 0.0045  8.0710  3.8415 0.0014  19.7588  11.0705 0.0007 28.7490 16.9190 0.0000 43.4200 22.3620 0.0159 31.8022 27.5871 0.0267 35.2250 32.6706
Indosat
p     Qstat   CV 0.0029  8.8761  3.8415 0.0050 16.7279 11.0705 0.0056 23.2624 16.9190 0.0178 25.8593 22.3620 0.0175 31.4599 27.5871 0.0314 34.5793 32.6706	p     Qstat   CV 0.0031  8.7417  3.8415 0.0349  11.9923  11.0705 0.0794 15.4465 16.9190 0.2293  16.3781 22.3620 0.3581  18.4982 27.5871 0.4690 20.8368 32.6706
Unilever
p     Qstat   CV 0.3604  0.8363  3.8415 0.5933  3.7004 11.0705 0.8039  5.3380 16.9190 0.9509  5.8658 22.3620 0.9684  7.9103 27.5871 0.9579 11.2400 32.6706	p     Qstat   CV 0.3624  0.8296  3.8415 0.6282  3.4682 11.0705 0.6991  6.4020  16.9190 0.9078  6.8877 22.3620 0.9370  9.1022 27.5871 0.9097 12.9704 32.6706
Telkom
p     Qstat   CV 0.1801  1.7965  3.8415 0.0933  9.4230 11.0705 0.1932 12.3718 16.9190 0.4219 13.3404 22.3620 0.4126 17.6286 27.5871 0.5590 19.4072 32.6706	p     Qstat   CV 0.1811  1.7883  3.8415 0.1224  8.6826 11.0705 0.1391  13.5552  16.9190 0.2821  15.4161 22.3620 0.2041 21.5155 27.5871 0.2649 24.5991 32.6706

Dari Tabel 3.1 dapat dilihat bahwa berdasarkan Uji Ljung-box residual kuadrat dan uji ARCH LM terhadap nilai dugaan residual kuadratnya diperoleh bahwa nilai Q lebih besar dari Critical Value (CV) atau nilai P lebih kecil dari a = 0,05 yang mengindikasikan tolak H₀ atau terima H₁ yang artinya nilai dugaan residual kuadrat IHSG berautokorelasi atau

tidak stasioner dan terdapat efek ARCH-GARCH pada data return IHSG sehingga memungkinkan peramalan menggunakan model GARCH. Penentuan model GARCH dapat dilihat dari plot ACF dan PACF residual kuadrat pada Gambar berikut

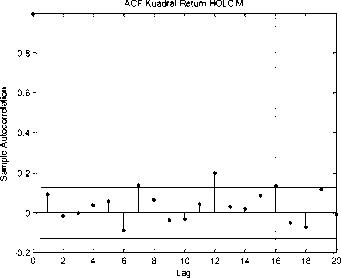
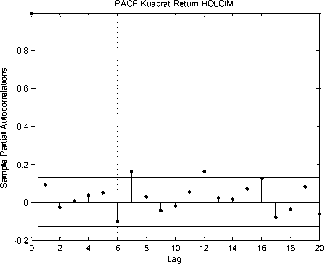
Peramalan dengan model GARCH akan dilakukan dengan mengestimasi parameterparameter model GARCH untuk memperoleh model GARCH yang terbaik. Beberapa model GARCH yang dapat dibentuk berdasarkan plot ACF dan PACF residual kuadrat IHSG dapat dilihat pada Tabel 3.2

Tabel 3.2. Model GARCH

Model	GARCH (1,1)	GARCH (1,2)	GARCH (2,1)	GARCH (2,2)
K	2e-007 [0.1055]	2e-007 [0.1083]	2e-007 [0.1040]	2e-007 [0.0620]
G1	0,9708 [27,5780]*	0.96969 [28.3250]*	0.97033 [0.3450]	0.081502 [0.5776]
G2			0.00048781 [0.0002]	0.86447 [5.7269]
A1	0,023387 [1.3407]		0.023371 [0.3581]
^2		0.024336 [0.3641]
AIC	-1.5792	-1.5776	-1.5772	-1.5772
BIC	-1.5654	-1.5603	-1.5599	1.5564

diketahui hasil estimasi koefisien model

GARCH     IHSG, dimana peramalan

menggunakan model GARCH (1,1) paling baik dibanding model GARCH yang lainnya. Hal ini dapat dilihat dari uji AIC dan BIC yang memberikan nilai minimum pada peramalan model GARCH (1,1). Sehingga model GARCH (1,1) pada IHSG adalah

Gt = 0,0000002 + 0,9708^σt-l

+ 0,023387 ^εt-ι

dengan ^σt adalah ramalan nilai variansi periode t, ^εt-ι adalah nilai residual periode t-1 , dan ^σt-ι adalah nilai variansi periode t-1 .

Tabel 3.3. Estimasi Parameter Model GARCH pada Holcim

Model	GARCH (1,1)	GARCH (1,2)	GARCH (2,1)	GARCH (2,2)
K	1.7014e-005 [1.5564]	1.6979e-005 [1.2872]	2.5803e-005 [1.4442]	2.58e-005 [1.3279]
G1	0.89166 [22.8302]*	0.89176 [17.2216]*	0.084879 [0.7989]	0.084899 [0.6078]
G2			0.74043 [6.4438]*	0.74041 [5.9838]*
A1	0.069975 [2.6688]*	0.069968 [1.8117]*	0.11548 [3.0235]*	0.11548 [2.8273]*
^2
AIC	-1.1838	-1.1818	-1.1842	-1.1822
BIC	-1.1700	-1.1645	-1.1669	-1.1615

Keterangan: tanda […]^∗ menunjukkan T-Stat > T-tab pada

a = 0,05

Berdasarkan Tabel 3.3 diketahui hasil estimasi koefisien model GARCH IHSG, dimana peramalan menggunakan model GARCH (1,1) paling baik dibanding model GARCH yang lainnya. Hal ini dapat dilihat dari uji AIC dan BIC yang memberikan nilai minimum pada peramalan model GARCH (1,1). Sehingga model GARCH (1,1) pada Holcim adalah

Ot =0,0017014 + 0.89166 Ot- + 0.069975 ^εt-ι dengan ^σt adalah ramalan nilai variansi periode t, ^εt-ι adalah nilai residual periode t-1 , dan of-t adalah nilai variansi periode t-1 .

Tabel 3.4 menunjukkan hasil estimasi koefisien model GARCH IHSG, dimana peramalan menggunakan model GARCH (1,1) paling baik dibanding model GARCH yang lainnya. Hal ini dapat dilihat dari uji AIC dan BIC yang memberikan nilai minimum pada peramalan model GARCH (1,1). Sehingga model GARCH (1,1) pada Indofood adalah

Gt = 0,0019365 + 0.76183 ^σt-l

+ 0.1268 ^εt-ι

dengan ^σt adalah ramalan nilai variansi periode t, ^εt-ι adalah nilai residual periode t-1 , dan ^σt-ι adalah nilai variansi periode t-1 .

Tabel 3.4. Estimasi Parameter Model GARCH pada Indofood

Model	GARCH (1,1)	GARCH (1,2)	GARCH (2,1)	GARCH (2,2)
K	1.9365e-005 [1.8892]*	1.9376e-005 [1.6658]*	5.5137e-007 [0.3238]	5.4817e-007 [0.3016]
Gi	0.76183 [7.4772]*	0.76187 [6.3123]*
G2			0.93618 [29.8967]*	0.93622 [27.0843]*
A1	0.1268 [2.2788]*	0.1267 [1.8563]*	0.051026 [2.7831]*	0.051015 [2.6557]*
^2
AIC	-1.4122	-1.4102	-1.4202	-1.4182
BIC	-1.3984	-1.3929	-1.4029	-1.3975

Keterangan: tanda […]^∗ menunjukkan T-Stat > T-tab pada

a = 0,05

Tabel 3.5 Estimasi Parameter Model GARCH pada Indosat

Model	GARCH (1,1)	GARCH (1,2)	GARCH (2,1)	GARCH (2,2)
K	1.7467e-005 [3.1300]*	1.7527e-005 [2.4390]*	1.745e-005 [2.9998]*	3.2945e-005 [3.0310]*
Gi	0.76615 [21.1240]*	0.76538 [14.0916]*	0.76632 [2.4319]*
G2				0.54682 [4.7066]*
Ar	0.18938 [4.6456]*	0.18823 [3.1080]*	0.18925 [3.1159]*	0.16089 [3.0757]*
^2		0.0017844 0.0267		0.21993 3.1189*
AIC	-1.3358	-1.3338	-1.3338	-1.3325
BIC	-1.3219	-1.3165	-1.3165	-1.3117

Keterangan: tanda […]^∗ menunjukkan T-Stat > T-tab pada a = 0,05

dengan melihat Tabel 3.5 diketahui hasil

estimasi koefisien model GARCH IHSG, dimana peramalan menggunakan model GARCH (1,1) paling baik dibanding model GARCH yang lainnya. Hal ini dapat dilihat dari uji AIC dan BIC yang memberikan nilai minimum pada peramalan model GARCH (1,1). Sehingga model GARCH (1,1) pada Indosat adalah

Gt = 0,0017467 + 0.76615 Gt-I

+ 0.18938 ^εt-ι

dengan ^σt adalah ramalan nilai variansi periode t, ^εt-l adalah nilai residual periode t-1 , dan Gt-I adalah nilai variansi periode t-1 .

Tabel 3.6. Estimasi Parameter Model GARCH

pada Unilever

Model	GARCH (1,1)	GARCH (1,2)	GARCH (2,1)	GARCH (2,2)
K	2e-007 [0.0602]	2e-007 [0.0588]	2e-007 [0.0365]	2e-007 [0.0291]
Gi	0.98736 [40.2778]*	0.98733 [39.5789]*	0.058022 [0.3352]	0.060979 [0.2575]
G2			0.91594 [5.5444]*
Ar	0.0088373 [0.8683]	0.0088629 [0.2168]	0.019531 [1.2163]	0.019494 [1.1531]
^2
AIC	-1.3305	-1.3285	-1.3293	-1.3273
BIC	-1.3167	-1.3112	-1.3120	-1.3065

Keterangan: tanda […]^∗ menunjukkan T-Stat > T-tab pada

a = 0,05

dengan melihat Tabel 3.6 diketahui hasil estimasi koefisien model GARCH IHSG, dimana peramalan menggunakan model GARCH (1,1) paling baik dibanding model GARCH yang lainnya. Hal ini dapat dilihat dari uji AIC dan BIC yang memberikan nilai minimum pada peramalan model GARCH (1,1). Sehingga model GARCH (1,1) pada Unilever adalah

Gt =0,0000002+0.98736^σt-l + 0.0088373 ^εt-l

dengan ^σt adalah ramalan nilai variansi periode t, ^εt-l adalah nilai residual periode t-1 , dan ^σt-l adalah nilai variansi periode t-1 .

Tabel 3.7. Estimasi Parameter Model GARCH pada Telkom

Model	GARCH (1,1)	GARCH (1,2)	GARCH (2,1)	GARCH (2,2)
K	5.5684e-005 [1.4115]	0.0001346 [2.4351]*	5.5735e-005 [1.1287]	0.00015687 [2.1471]*
Gi	0.70715 [3.9479]*	0.28013 [1.1288]	0.70696 [0.9094]
G2				0.16534 [0.7245]
Ar	0.091605 [1.8646]*	0.057514 [0.9304]	0.091648 [1.0747]	0.066124 [1.1147]
^2		0.19186 [2.5018]*		0.21945 [2.8288]*
AIC	-1.2848	-1.2869	-1.2828	-1.2857
BIC	-1.2710	-1.2696	-1.2655	-1.2649

Keterangan: tanda […]^∗ menunjukkan T-Stat > T-tab pada

a = 0,05

Berdasarkan Tabel 3.7 diketahui hasil estimasi koefisien model GARCH Telkom, dimana peramalan menggunakan model GARCH (1,1) paling baik dibanding model GARCH yang lainnya. Hal ini dapat dilihat dari uji AIC dan BIC yang memberikan nilai minimum pada peramalan model GARCH (1,1). Sehingga model GARCH (1,1) pada Telkom adalah

Ot =0,0055684 +0.70715^σt-ι + 0.091605^εt-ι

dengan ^σt adalah ramalan nilai variansi periode t, ^εt-l adalah nilai residual periode t-1 , dan ^σt-ι adalah nilai variansi periode t-1 .

Tahap selanjutnya dalam peramalan menggunakan model GARCH setelah dilakukan estimasi dan diperoleh model terbaik adalah melakukan uji Ljung-Box terhadap residual kuadrat yang distandarisasi (Z^ ) dan uji ARCH terhadap residual yang distandarisasi (Z^ )dari model yang diperoleh.

Tabel 3.8 Uji Ljung-Box Residual IHSG Setelah Estimasi

Saham IHSG
Uji Ljung Box p     Qstat   CV 0.6403  0.2184  3.8415 0.4525  4.7082 11.0705 0.7405  5.9942 16.9190 0.7448  9.3659 22.3620 0.7453  12.8633 27.5871 0.5220 19.9888 32.6706	Uji ARCH LM p     Qstat   CV 0.5686  0.3250  3.8415 0.7462  2.6992 11.0705 0.9209  3.8514 16.9190 0.9689  5.2649 22.3620 0.9829  7.0463 27.5871 0.4331 21.4276 32.6706
Holcim
p      Qstat CV 0.4028  0.6998  3.8415 0.7425  2.7238 11.0705 0.2749 11.0116 16.9190 0.4845 12.5334 22.3620 0.2785 19.9177 27.5871 0.3430 23.0190 32.6706	p      Qstat CV 0.3571  0.8481  3.8415 0.8591  1.9271  11.0705 0.4521  8.8409 16.9190 0.6879 10.0742 22.3620 0.7698 12.4877 27.5871 0.9047 13.1105 32.6706
Indofood
p     Qstat   CV 0.9654  0.0019  3.8415 0.7755  2.5064 11.0705 0.7646  5.7505 16.9190 0.9198  6.6379 22.3620 0.9796  7.2788 27.5871 0.9914  8.6974 32.6706	p     Qstat   CV 0.8629  0.0298  3.8415 0.9973  0.3167 11.0705 1.0000  0.4884 16.9190 1.0000  0.6235 22.3620 1.0000  0.6771 27.5871 1.0000  0.8404 32.6706
Indosat
p     Qstat   CV 0.9453  0.0047  3.8415 0.8803  1.7677 11.0705 0.9007  4.1586 16.9190 0.9649  5.4156 22.3620 0.9755  7.5368 27.5871 0.9938  8.2950 32.6706	p     Qstat   CV 0.8651  0.0289  3.8415 0.9978  0.2909 11.0705 0.9999  0.5631  16.9190 1.0000  0.8041 22.3620 1.0000  1.0305 27.5871 1.0000  1.3315 32.6706

Unilever
p	Qstat	CV	p	Qstat	CV
0.4731	0.5146	3.8415	0.9920	0.0001	3.8415
0.9380	1.2703	11.0705	0.8499	1.9946	11.0705
0.9824	2.4434	16.9190	0.9793	2.5583	16.9190
0.9953	3.5152	22.3620	0.9975	3.1171	22.3620
0.9945	5.7876	27.5871	0.9997	3.6389	27.5871
0.9934	8.3720	32.6706	0.9994	6.0715	32.6706
Telkom
p	Qstat	CV	p	Qstat	CV
0.5588	0.3418	3.8415	0.6534	0.2016	3.8415
0.4850	4.4616	11.0705	0.2047	7.2209	11.0705
0.4820	8.5278	16.9190	0.2216	11.8544	16.9190
0.6921	10.0229	22.3620	0.4975	12.3711	22.3620
0.6575	14.1348	27.5871	0.7093	13.3963	27.5871
0.7435	16.4557	32.6706	0.8305	14.8476	32.6706

dengan melihat Tabel 3.8 dapat dilihat bahwa berdasarkan Uji Ljung-box residual kuadrat yang distandarisasi ( ^t) dan uji ARCH LM terhadap nilai dugaan residual kuadratnya diperoleh bahwa nilai Q lebih kecil dari Critical Value (CV) atau nilai P lebih besar dari a = 0,05 yang mengindikasikan tolak Hq atau terima Hy yang artinya nilai dugaan residual kuadrat IHSG sudah tidak berautokorelasi atau stasioner dan sudah tidak terdapat efek ARCH-GARCH dalam residual.

• C.    Perhitungan Nilai Beta Saham Unggulan

Tabel 3.9. Nilai beta pasar dari saham unggulan.

Nama Saham	Nilai Beta Saham	Variansi
IHSG	0.0092	8.3931e-005
HOLCIM	0.0208	4.3457e-004
INDOFOOD	0.0133	1.7749e-004
INDOSAT	0.0161	2.5803e-004
UNILEVER	0.0153	2.3389e-004
TELKOM	0.0169	2.8402e-004

Berdasarkan Tabel 3.9 terlihat bahwa perhitungan beta pasar berada dalam kelompok β<1 dimana saham unggulan memiliki risiko lebih rendah dari risiko pasar. Nilai beta tertinggi dimiliki oleh saham HOLCIM dengan β = 0.0208 dengan risiko saham sebesar 4.3457e-004. Hal ini sesuai dengan asumsi bahwa semakin besar nilai beta suatu saham maka semakin tinggi tingkat risiko saham tersebut dan semakin besar pula pengembalian yang diberikan saham tersebut.

Tabel 3.10. Nilai Beta Pasar dari Saham Unggulan Menggunakan Model GARCH.

Nama Saham	Nilai Beta Saham	Variansi
HOLCIM	0.3107	0.0965
INDOFOOD	0.1808	0.0327
INDOSAT	0.2881	0.0830
UNILEVER	0.1041	0.0108
TELKOM	0.2086	0.0435

Berdasarkan Tabel 3.10 terlihat bahwa perhitungan beta pasar berada dalam kelompok β<1 dimana saham unggulan memiliki risiko lebih rendah dari risiko pasar. Nilai beta tertinggi dimiliki oleh saham HOLCIM dengan β = 0.3107 dengan risiko saham yang ditanggung sebesar 0.0965. Hal ini sesuai dengan asumsi bahwa semakin besar nilai betasuatu saham maka semakin tinggi tingkat risiko saham tersebut dan semakin besar pula pengembalian yang diberikan saham tersebut.

D. Perbandingan Nilai Beta Saham Unggulan

Beta Pasar Saham Unggulan
Nama Saham	Nilai Beta	Variansi
HOLCIM	0.0208	4.3457e-004
INDOFOOD	0.0133	1.7749e-004
INDOSAT	0.0161	2.5803e-004
UNILEVER	0.0153	2.3389e-004
TELKOM	0.0169	2.8402e-004

Beta Pasar Saham Model GARCH
Nama Saham	Nilai Beta	Variansi
HOLCIM	0.3107	0.0965
INDOFOOD	0.1808	0.0327
INDOSAT	0.2881	0.0830
UNILEVER	0.1041	0.0108
TELKOM	0.2086	0.0435

Pada tabel di atas terlihat bahwa nilai beta menggunakan model GARCH lebih besar dibandingkan beta pasar saham unggulan. Semakin besar nilai beta yang diperoleh maka saham tersebut semakin baik digunakan dalam berinvestasi. Selain beta nilai variansi atau risiko juga sangat penting dalam melakukan investasi saham. Terlihat bahwa variansi model GARCH lebih besar dibandingkan beta pasar saham unggulan. Semakin besar risiko yang dihadapi oleh investor maka semakin besar keuntungan yang diperoleh.

• 4.    KESIMPULAN DAN SARAN

Berdasarkan uraian dan analisisnya, dapat diambil kesimpulan saham-saham unggulan pada periode 23 September 2013 sampai 24 September 2014 memperoleh β<1 dimana saham unggulan memiliki risiko lebih rendah dari risiko pasar. Dan berdasarkan perhitungan beta pasar saham unggulan dan diperoleh nilai beta menggunakan model GARCH lebih besar dibandingkan dibandingkan nilai beta pasar.

Dari penelitian di atas maka saran yang dapat penulis berikan adalah untuk investor yang berminat untuk melakukan investasi dengan menanam modalnya di bursa saham namun bukan bertujuan untuk spekulasi semata, sangat penting untuk melakukan analisa terhadap kinerja saham tersebut terlebih dahulu sehingga dapat mengetahui tingkat risiko dan tingkat pengembalian dari masing-masing saham dan untuk penelitian selanjutnya selain model GARCH dapat digunakan metode lain dalam pehitungan beta saham seperti metode CAPM dan juga lebih banyak lagi jenis saham yang dibandingkan nilai β, misalnya indeks sektoral atau indeks LQ45.

DAFTAR PUSTAKA

• [1]    Agus Sartono. 1999. Manajemen

Keuangan.edisi 3. BPFE UGM.

• [2]    Ang, R. 1997. Pasar Modal Indonesia. Media SoftIndonesia. Jakarta.

• [3]    Bollerslev, T.et all. 1986. Glosary to ARCH (GARCH). Volatility and Time Series 8,137-164.

• [4]    Francis, Jack Clark. Wiley Finance, Volume 795. Modern Portofolio Theory+WS. Foundations, Analysis, and New Developments. Wiley, p. 311.

• [5]    Husnan, Suad. 1998. Dasar-dasar Teori Portofolio. UPP AMP YKPM. Yogyakarta.

• [6]    Hwang. SY., Basawa, I.V. Stationarity and Moment Structure for Box Coxtransformed Threshold GARCH(1,1) Processes. Journal Statistics and Probability Letters, 68 (20040, 209) A, S220.

• [7]    Jogiyanto, Hartono 1998. Teori Portofolio dan Analisis Sekuritas.edisi ketiga. BPFE. Yogyakarta.

• [8]    Jogiyanto, Hartono 2000. Teori Portofolio dan Analisis Investasi. edisi keempat. BPFE. Yogyakarta.

• [9]    Luenberger, D.G. 1998. Investment Science.Oxford University Press. New York.

• [10]    Riyanto, B. 1999. Dasar-dasar Pembelanjaan Perusahaan. BPFE. Yogyakarta.

• [11]    Sawidji, Widoatmojo. 1996. Cara Sehat Investasi di Pasar Modal. Jakarta: Jurnalindo Aksan Grafika.

• [12]    Weston, J. Fred dan Thomas E. Copeland. 1995. Manajeman Keuangan Jilid I, Edisi Keempat, Bina Aksara-Jakarta.

75