PENERAPAN METODE BOOTSTRAP RESIDUAL DALAM MENGATASI BIAS PADA PENDUGA PARAMETER ANALISIS REGRESI

E-Jurnal Matematika Vol. 3 (4), November 2014, pp. 130-137

ISSN: 2303-1751

PENERAPAN METODE BOOTSTRAP RESIDUAL DALAM MENGATASI BIAS PADA PENDUGA PARAMETER ANALISIS REGRESI

Ni Made Metta Astari^§1, Ni Luh Putu Suciptawati², I Komang Gde Sukarsa³

¹Jurusan Matematika, Fakultas MIPA - Universitas Udayana [Email: [email protected]] ²Jurusan Matematika, Fakultas MIPA - Universitas Udayana [Email: [email protected]] ³Jurusan Matematika, Fakultas MIPA - Universitas Udayana [Email: [email protected]] ^§Corresponding Author

ABSTRACT

Statistical analysis which aims to analyze a linear relationship between the independent variable and the dependent variable is known as regression analysis. To estimate parameters in a regression analysis method commonly used is the Ordinary Least Square (OLS). But the assumption is often violated in the OLS, the assumption of normality due to one outlier. As a result of the presence of outliers is parameter estimators produced by the OLS will be biased. Bootstrap Residual is a bootstrap method that is applied to the residual resampling process. The results showed that the residual bootstrap method is only able to overcome the bias on the number of outliers 5% with 99% confidence intervals. The resulting parameters estimators approach the residual bootstrap values OLS initial allegations were also able to show that the bootstrap is an accurate prediction tool.

Keywords: regression analysis, outlier, biases, bootstrap residuals

• 1.    PENDAHULUAN

Analisis statistik yang bertujuan untuk menganalisa suatu hubungan linier antara peubah bebas (x) dan peubah tak bebas (y) dikenal dengan analisis regresi. Istilah regresi pertama kali dikembangkan oleh Sir Francis Galton di akhir abad ke-19.

Analisis regresi linier sederhana merupakan analisis regresi yang melibatkan hanya satu peubah bebas dan satu peubah tak bebas [1]. Model untuk analisis regresi linier sederhana dapat dituliskan sebagai berikut:

^ ⁼ ^O + βl^i + ^εi           (1)

Untuk menduga parameter dalam analisis regresi, metode yang umum digunakan adalah Metode Kuadrat Terkecil (MKT). MKT dapat digunakan apabila asumsi-asumsi pada analisis regresi terpenuhi. Salah satu asumsi penting yang harus dipenuhi adalah asumsi kenormalan.

Namun sering kali asumsi kenormalan tersebut dilanggar pada data yang mengandung pencilan.

Pencilan merupakan suatu data amatan yang ekstrim [1]. Pencilan tidak dapat dibuang diabaikan, karena mungkin pencilan tersebut memberikan informasi penting yang tidak bisa diberikan oleh data lainnya. Akibat dari adanya pencilan adalah penduga parameter yang dihasilkan oleh MKT akan bersifat bias. Bias pada penduga parameter akan mengakibatkan penduga yang dimiliki kehilangan sifat Best Linear Unbiased Estimator (BLUE).

Bootstrap merupakan metode simulasi berbasis data yang digunakan dalam pendugaan parameter dan penyusunan selang kepercayaan tanpa perlu mengetahui distribusi populasi dari sampel yang dimiliki. Metode bootstrap pertama kali diperkenalkan oleh Efron pada tahun 1979. Nama bootstrap sendiri diambil

dari sebuah frase “ to pull oneself up by one’s bootstraps” yang berarti berdiri di atas kaki sendiri [2]. Pendekatan pada bootstrap ini menggunakan metode pengambilan sampel berulang (resample).

Berdasarkan karakteristik metode bootstrap yang merupakan metode simulasi berbasis data dan tanpa mengetahui distribusi populasi dari sampel yang dimiliki, penulis ingin mengetahui apakah metode bootstrap residual mampu dalam mengatasi bias pada penduga parameter akibat adanya pencilan pada bagian bawah gugus data pada analisis regresi linier.

• 2.    TINJAUAN PUSTAKA

  • 2.1.    Metode Kuadrat Terkecil

Metode Kuadrat Terkecil (MKT) atau Ordinary Least Square (OLS) adalah salah satu metode yang paling umum digunakan dalam analisis regresi yang bertujuan untuk meminimumkan kuadrat kesalahan ε_i sehingga nilai regresinya mendekati nilai yang sesungguhnya. MKT merupakan metode yang digunakan untuk mendapatkan penduga yang baik bagi parameter regresi Pq dan Pl [1].

Agar menjadi penduga yang baik maka penduga MKT harus memiliki ukuran tingkat akurasi penduga parameter, yaitu [1]:

• a.    Bersifat linier n ⅛ι y∕<_r^_r

Selang kepercayaan untuk ^O b₀ + t(l — a∕2∙,n — 2)s{b₀}

• 2.3.    Bootstrap Residual

Bootstrap residual merupakan metode simulasi berbasis data yang proses resamplingnya diterapkan pada residual yang dihasilkan oleh model analisis regresi [2].

Sampel bootstrap residual didefinisikan sebagai suatu sampel acak berukuran n yang

∧

diambil       dari       F ,       misalkan

e* = (e^e*,...,e*) , atau dapat dinyatakan

sebagai berikut[2]:

P →(ep⅛.....e;) = e*     (2)

Langkah-langkah dalam bootstrap residual sebagai berikut [3]:

• 1 .Menentukan nilai ¥ dari penduga parameter yang dihasilkan oleh MKT. Y diperoleh dengan perhitungan

Y = ⅛ + ⅛.       (3)

• 2 .Menentukan model regresi linier sehingga

menghasilkan residual. Nilai residual diperoleh dengan menghitung selisih antara Y_i dan Y yaitu,

e = Y_i-Y.            (4)

• 3 .Mengambil n sampel acak dengan pengembalian dari e₁,e₂,..._re_nsehingga menghasilkan e* = (⅛e.....<).

• 4 .Menghitung nilai bootstrap untuk Y*

  
  
  

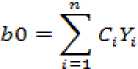
dengan menambahkan e* sehingga menghasilkan:

Y* = β₀+β₁X+e*     (5)

• b.    Tidak bias

«w=&

^{^o) ⁼ Pq

• c.    Selang Kepercayaan Penduga Parameter

Selang kepercayaan untuk A₁

b_i + t(l — a/2; n — 2)s{⅛₁}

• 5. Menghitung koefisien regresi untuk sampel bootstrap Y* dengan X sehingga diperoleh P''.

• 6. Ulangi langkah 2, 3, dan 4 sesuai dengan jumlah replikasi yang diinginkan.

• 3.    METODE PENELITIAN

Penelitian ini diawali dengan membangkitkan data simulasi dengan parameter regresi $& dan Pl sehingga membentuk model regresi linier sederhana.

Data simulasi terdiri dari satu peubah bebas dan galat yang kemudian digunakan untuk menentukan peubah tak bebas. Peubah bebas dibangkitkan sesuai model regresi linier sederhana. Membangkitkan data simulasi dilakukan dengan bantuan program R-2.15.3

Langkah-langkah membangkitkan data simulasi univariat adalah sebagai berikut:

• a. Menentukan peubah bebas ( X ) sebanyak 60 amatan, berupa 60 bilangan asli pertama, yaitu 1,2,3,...,60.

b.Membangkitkan nilai sisaan ( ε ) yang berdistribusi normal dengan rataan 0 dan ragam 1. Nilai sisaan yang dibangkitkan berukuran 60.

• c. Menentukan hubungan dari peubah tak bebas dan peubah bebas yaitu y = ⅛ + ⅛x + _s . Nilai parameter yang digunakan adalah Po — ^ dan Pi = ^, dan 5 .

d.Menentukan nilai-nilai Y dari bentuk hubungan pada langkah ( c ).

Pembangkitan data sisaan yang mengandung pencilan pada data simulasi dibagi menjadi 3 kelompok, yaitu 5%, 10%, dan 15% adalah sebagai berikut:

• a. Pembangkitan data sisaan yang mengandung pencilan sebesar 5% , yaitu dengan jumlah data 5% dari 60 data, rataan 5 dan standar deviasi 0,1.

b.Pembangkitan data sisaan yang mengandung pencilan sebesar 10% , yaitu dengan jumlah data 10% dari 60 data, rataan 5 dan standar deviasi 0,1.

• c. Pembangkitan data sisaan yang mengandung pencilan sebesar 15% , yaitu dengan jumlah data 15% dari 60 data, rataan 5 dan standar deviasi 0,1.

Data simulasi kemudian diuji asumsi kenormalannya dengan uji Anderson-Darling, dan dengan diagram pencar untuk melihat kembali pencilan yang telah dibangkitkan dengan bantuan program R-2.15.3. Nilai p-value pada Uji Anderson-Darling akan dibandingkan dengan α sebesar 0,05.

Hipotesis yang digunakan adalah:

^o : data mengikuti sebaran normal

^l : data tidak mengikuti sebaran normal Keputusan menolak ¾ jika p-value lebih kecil dari α.

Selanjutnya penduga parameter Pq dan Pl pada data simulasi akan diduga dengan MKT dan untuk melihat bias dari penduga parameter, akan diuji dengan selang kepercayaan 95% dan 99%. Pendugaan parameter Pq dan Pl akan diduga kembali dengan metode bootstrap residual dengan resampling sebanyak 250, 500, 1.000, 5.000, 10.000, 50.000, 75.000, dan 100.000 kali. Bias dari penduga parameter akan diuji dengan seang kepercyaan bootstrap, dan asumsi kenormalannya akan diuji kembali dengan uji Anderson-Darling. Hasil dari pendugaan dengan kedua metode tersebut kemudian akan dianalisa dan dibandingkan.

• 4. HASIL DAN PEMBAHASAN

• A.    Membangkitkan Data Simulasi

Dalam penelitian ini data yang digunakan adalah data simulasi yang dibangkitkan dengan bantuan program R-2.15.3. Data yang dibangkitkan adalah data univariat yaitu dengan peubah tak bebas (Y) dan peubah bebas (X) sehingga bentuk hubungannya seperti pada persamaan (1) sebagai berikut:

Y_i = β₀ + β₁X_i+ε_i

dengan E_i adalah nilai sisaan yang berdistribusi normal dengan ragam 1 dan rataan 0. Peubah bebas (X) yang dibangkitkan merupakan nilai konstanta yang ditentukan nilainya dan dalam penelitian ini nilai peubah bebas (X) bernilai: 1,2,3,…,60. Peubah tak bebas (Y) diperoleh dengan terlebih dahulu memisalkan nilai parameternya. Nilai parameter yang digunakan adalah ft Q = 2 dan Pl = 1, 3, dan 5. Dari nilai yang diketahui yaitu dari peubah bebas (X) dan parameternya maka diperoleh nilai untuk peubah tak bebas (Y) sesuai dengan bentuk hubungan pada (1). Data awal adalah nilai dari peubah tak bebas (Y), peubah bebas (X) dan sisaan (E_i ) merupakan data awal yang belum mengandung pencilan.

Simulasi pada data kemudian dilakukan dengan memasukkan pencilan sebesar 5%, 10%, dan 15% pada data awal yang tidak mengandung pencilan. Nilai pencilan yang

digunakan pada penelitian ini diperoleh dengan memasukkan nilai sisaan dari sebaran normal dengan rataan 5 dan standar deviasi 0,1 (N(5;0,1)) ke dalam kelompok data sisaan awal dari sebaran data normal dengan ragam 1 dan rataan 0 (N(0,1)).

Data yang telah dibangkitkan baik data awal tanpa pencilan maupun data yang telah mengandung pencilan, selanjutnya dianalis menggunakan diagram pencar dengan bantuan program R-2.15.3. Tahapan ini dimaksudkan hanya untuk memeriksa kembali apakah data simulai mengandung pencilan atau tidak. Pada diagram pencar, adanya pencilan akan ditunjukkan dengan adanya data amatan yang tidak berada pada garis regresi. Nilai yang akan dianalisis adalah nilai variabel x dan y sebelum dan sesudah dimasukkan pencilan.

• B.    Hasil Pengujian Asumsi Kenormalan dengan Uji Anderson-Darling dan Pendugaan Parameter A dengan MKT

Tabel 1. Hasil Pengujian Asumsi Kenormalan dengan Uji Anderson-Darling

⅛iffl⅛	Alpha (α)	p-value	⅛≡
⅛p∙	0,05	0,4151	Noimal
P.5%	0,05	0,0001542	Iislafciiomial
P.10%	0,05	6,635e-07	Mnomial
P.15%	0,05	1,61M8	Miiomial
⅛P.	0,05	02094	Nornial
P.5%	0,05	l,849e-05	Mnomial
P.10%	0,05	2,115e-07	Miiomial
P.15%	0,05	2,09M9	Miiomial
⅛P∙	0,05	0,5039	Nornial
P.5%	0,05	⅛H	Mnomial
P.10%	0,05	2,O87e-O7	Mnomial
P.15%	0,05	4J48e-10	Mnomial

Sesuai hasil uji kenormalan dengan Uji Anderson-Darling, dapat dilihat pada tabel 1 bahwa pada data dengan nilai parameter ^l =1, $1=3, dan β₁=5, data tanpa pencilan memiliki p-value yang lebih besar dari nilai α sebesar

0,05, ini menunjukkan bahwa data awal tanpa pencilan mengikuti sebaran normal. Sedangkan pada data dengan nilai βl=1, βl=3, dan βl=5, data yang memiliki pencilan sebesar 5%, 10%, dan 15%, memiliki nilai p-value yang lebih kecil dari α sebesar 0,05, ini menunjukkan bahwa data yang mengandung pencilan tidak mengikuti sebaran normal.

Berdasarkan Tabel 2 dapat dilihat bahwa pada data simulasi dengan nilai βl=1, βl=3, dan β₁ =5 untuk data tanpa pencilan, nilai parameter βl terkandung di dalam selang kepercayaan 95% dan 99%. Hal ini berarti penduga parameter regresi yang dihasilkan oleh MKT tidak mengalami bias. Di lain pihak untuk data berpencilan 5% pada βl=1 dan βl=3, penduga parameter tidak bias pada selang kepercayaan 99%. Pada data berpencilan 10% dan 15%, selang kepercayaan yang dihasilkan tidak memuat nilai parameter, sehingga penduga parameter βl yang dihasilkan mengalami bias.

Tabel 2. Pendugaan Parameter dengan MKT

Mah p⅛		⅛⅛≡ffl^		⅛⅛j≡99%
		⅛	ta,WW	Iepwcayaan	⅛JJJM
⅛p.	0,998	0,984-1,0127	M⅛s	0,979-1,017	MBias
P.5%	0,976	0,956 -0,996	Bias	0,949 - 1,003	MBias
P.10%	0,956	0,933 -0,979	Bias	0,925 -0,986	Bias
P.15%	0,940	0,915-0,965	Bias	0,907-0,973	Bias
⅛P∙	2,996	2,979-3,013	MBias	2,974-3,019	MBias
P.5%	2,973	2,951 -2,995	Bias	2,944-3,002	MBias
P.10%	2,951	2,927-2,975	Bias	2,919-2,983	Bias
P.15%	2,934	2.909 -2.959	Bias	2,900-2.967	Bias
⅛P∙	4,999	4,981-5,016	MBias	4,976-5,022	MBias
P.5%	4,969	4,948 -4,990	Bias	4,941 -4,997	Bias
P.10%	4,951	4,927-4,974	Bias	4,919-4,982	Bias
P.15%	4,932	4,908-4,957	Bias	4,900 -4,965	Bias

• C.    Pendugaan Parameter A dengan Metode Bootstrap Residual dan Uji Asumsi Kenormalan dengan Uji Anderson-Darling

Berdasarkan Tabel 3 data simulasi dengan nilai Pl=1, pada data berpencilan 5%, selang kepercayaan 95% dan 99% yang dihasilkan metode bootstrap residual memuat nilai parameter Pl sehingga penduga yang dihasilkan tidak mengalami bias. Di lain pihak data berpencilan 10% dan 15% dengan jumlah resampling yang sama, penduga parameter yang dihasilkan mengalami bias.

Tabel 3. Pendugaan Parameter A. = 1 dengan Bootstrap Residual

M⅛ p.encihη		⅛⅛3≡9i!i		⅛⅛a99!i
			⅛Λ		Kstsaiigii
			=250
P.5%	0,976	0,949- 1,004	WBiis	0,941-1,012	WBias
P.10%	0,956	0,927-0,985	Bias	0,918-0,994	Bias
Pli∖	0,934	0,906-0,963	Bias	0,897 4),972	Bias
			=500
P.5%	0,976	0,949-1,003	WBias	0,940-1,011	WBias
P.10%	0,956	0,926- 0,984	Bias	0,917-0,993	Bias
P.15%	0,934	0,905 - 0,961	Bias	0,897-0,969	Bias
B=LOOO
P.5%	0,976	0,948- 1,003	WBias	0,940-1,011	WBias
P.10%	0,956	0,927- 0,985	Bias	0,918-0,994	Bias
P.15%	0,934	0,905 - 0,961	Bias	0,896 -0,970	Bias
B=5,000
P.5%	0,976	0,949-1,002	WBias	0,940-1,010	WBias
P.10%	0,956	0,926-0,985	Bias	0,916-0,994	Bias
P.15%	0,934	0,906 - 0,962	Bias	0,897-0,970	Bias

B=10.000
P.5%	0,976	0,948-1,002	WBias	0,940 - 1,010	WBias
P.10%	0,956	0,926- 0,986	Bias	0,916-0,995	Bias
P.15%	0,934	0,906 -0,962	Bias	0,897-0,970	Bias
B=50.000
P.5%	0,976	0,949-1,002	WBias	0,940 - 1,011	WBias
P.10%	0,956	0,926-0,985	Bias	0,916-0,995	Bias
P.15%	0,934	0,906 - 0,961	Bias	0,898-0,970	Bias
B=75.000
P.5%	0,976	0,949-1,002	WBias	0,940- 1,011	WBias
P.10%	0,956	0,926-0,986	Bias	0,917-0,995	Bias
P.15%	0,934	0,9068-0,9619	Bias	0,898-0,970	Bias
B=100.000
P.5%	0,976	0,949-1,002	WBias	0,940 -1,011	WBias
P.10%	0,956	0,926- 0,986	Bias	0,917-0,995	Bias
P.15%	0,934	0,906 - 0,961	Bias	0,897-0,970	Bias

Pada Tabel 4 dapat dilihat bahwa pada data simulasi dengan pencilan 5% setelah diresampling dengan metode bootstrap residual, selang kepercayaan 99% yang dihasilkan memuat nilai parameter sehingga dapat disimpulkan bahwa penduga parameter yang dihasilkan tidak bias. Pada data simulasi berpencilan 5% pada selang kepercayaan 95% dan pada data berpencilan 10% dan 15% pada selang kepercayaan 95% dan 99% menghasilkan penduga parameter yang bias.

Pada Tabel 5 dapat dilihat bahwa pada data simulasi dengan pencilan 5%, selang kepercayaan 99% yang dihasilkan oleh metode bootstrap residual memuat nilai parameter sehingga penduga parameter yang dihasilkan tidak bias.

Tabel 4. Pendugaan Parameter β₁ = 3 dengan Bootstrap Residual

MA f,ffl⅛		Sdang Upsrcayaaa95 %		Sdang Upsrcayaan 99%
		Sdang Upsrcayaaa	Sstsrangan	Sdang Upsrcayaan	Ketsrangan
B-250
P.5%	2,970	2,946-2,995	Bias	2,938-3,OO3	Ttdak Bias
P.10%	2,951	2,925-2,976	Bias	2,917-2,984	Bias
P.15%	2,934	2,910-2,959	Bias	2,903-2,966	Bias
B=500
P.5%	2,970	2,947-2,994	Bias	2,940-3,001	MikBias
P.10%	2,951	2,924-2,978	Bias	2,916-2,986	Bias
P.15%	2,934	2,908-2,960	Bias	2,900-2,968	Bias
B=LOOO
P.5%	2,970	2,945-2,994	Bias	2,937-3,002	MakBias
P.10%	2,951	2,924-2,977	Bias	2,915-2,985	Bias
P.15%	2,934	2,907-2,961	Bias	2,899-2,969	Bias
B=5.000
P.5%	2,970	2,946-2,995	Bias	2,938-3,002	Bkbias
P.10%	2,951	2,925-2,977	Bias	2,916-2,986	Bias
P.15%	2,934	2,907-2.961	Bias	2,899-2,970	Bias
B=10.000
P.5%	2,970	2,946-2,995	Bias	2,938-3,002	Makbias
P.10%	2,951	2,925- 2,978	Bias	2,916-2,986	Bias
P.15%	2,934	2,908- 2,961	Bias	2,899-2,969	Bias
B=50,000
P.5%	2,970	2,946 -2,995	Bias	2,938-3,002	Makbias
P.10%	2,951	2,924-2,977	Bias	2,916-2,986	Bias
P.15%	2,934	2,908-2,961	Bias	2,899- 2,969	Bias
B=75.000
P.5%	2,970	2,946- 2,994	Bias	2,938-3,002	Makbias
P.10%	2,951	2,925- 2,977	Bias	2,916-2,986	Bias
P.15%	2,934	2,908- 2,961	Bias	2,899-2,969	Bias
B=100.000
P.5%	2,970	2,946-2,994	Bias	2,938-3,002	Makbias
P.10%	2,951	2,925-2,977	Bias	2,916-2,986	Bias
P.15%	2,934	2,908-2,961	Bias	2,899-2,969	Bias

Tabel 5. Pendugaan Parameter βι = 5 dengan Bootstrap Residual

Wah p.eιxc⅛an		⅛⅛ ⅛ ⅛≡≡	J«J5% ta.W®	⅛⅛ ⅛ Kepeicayaaii	ιy≡w% taw®
			3=250
P.5%	4,970	4,944-4,996	Bias	4,935-5,005	Makbias
P.10%	4,951	4,924-4,979	Bias	4,916-4,988	Bias
P.15%	4,932	4,906-4,958	Bias	4,898-4,966	Bias
			3=500
P.5%	4,970	4,944-4,996	Bias	4,936- 5,004	Makbias
P.10%	4,951	4,923-4,976	Bias	4,915-4,985	Bias
P.15%	4,932	4,907-4,959	Bias	4,899-4,967	Bias
B=L000
P.5%	4,970	4,946-4,995	Bias	4,938-5,003	Makbias
P.10%	4,951	4,924-4,978	Bias	4,915-4,986	Bias
P.15%	4,932	4,905-4,958	Bias	4,897-4,967	Bias
			= 5.000
P.5%	4,970	4,945-4,995	Bias	4,937-5,003	Makbias
P.10%	4,951	4,923-4,9'9	Bias	4,914-4,988	Bias
P.15%	4,932	4,905-4,960	Bias	4,896-4,968	Bias
B=10.000
P.5%	4,970	4,945-4,995	Bias	4,937-5,003	M⅛bias
P.10%	4,951	4,923-4,979	Bias	4,914-4,987	Bias
P.15%	4,932	4,905-4,959	Bias	4,897-4,968	Bias
B=50.000
P.5%	4,970	4,944-4,995	Bias	4,936-5,003	Makbias
P.10%	4,951	4,923-4,979	Bias	4,914-4,988	Bias
P.15%	4,932	4,905-4,959	Bias	4,896-4,968	Bias
P.5%	4,970	4,944-4,995	Bias	4,936-5,003	Makbias
P.10%	4,951	4,923-4,979	Bias	4,914-4,988	Bias
P.15%	4,932	4,905-4,959	Bias	4,896-4,968	Bias
B=75.000
P.5%	4,970	4,945-4,995	Bias	4,937-5,003	Mak bias
P.10%	4,951	4,923-4,979	Bias	4,914-4,987	Bias
P.15%	4,932	4,905-4,959	Bias	4,896-4,968	Bias
B=100.000
P.5%	4,970	4,945-4,995	Bias	4,937-5,003	Makbias
P.10%	4,951	4,923-4,979	Bias	4,914-4,987	Bias
P.15%	4,932	4,905-4,959	Bias	4,896-4,968	Bias

Data simulasi yang telah diresampling dengan metode bootstrap residual, asumsi kenormalannya diuji dengan Uji Anderson-Darling.

Tabel 6. Pengujian Asumsi Kenormalan pada Data yang Telah Diresampling dengan Uji Anderson-Darling

⅛ijffl⅛	Alpha (α)	p-valus	⅛≡
Λ=ι
P.5%	0,05	0,000'996	WswmI
P.10%	0,05	0,02893	WjwmI
P.15%	0,05	0,05444	Nomial
Λ=3
P.5%	0,05	0,002637	Wiiiomial
P.10%	0,05	0,01204	Wiiiomial
P.15%	0,05	0,06061	Nornial
Λ=5
P.5%	0,05	0,003931	Wiiiomial
P.10%	0,05	0,01703	Wiiiomial
P.15%	0,05	0,01663	Wiiiomial

Berdasarkan Tabel 6 dapat dilihat bahwa pada data simulasi berpencilan 15% dengan β₁ = 1 dan P₁ = 3, nilai –p-value yang dihasilkan lebih besar dari alpha (α) 0,05 sehingga dapat disimpulkan bahwa data menyebar normal. Pada data berpencilan 5% dan 10% p-value lebih kecil dari alpha (α) 0,05 sehingga dapat disimpulkan data tidak mengikuti sebaran normal. Pada data simulasi dengan nilai Pl = 5, data simulasi dengan pencilan 5%, 10%, dan 15% tidak menyebar normal.

• D.    Menganalisa dan Membandingkan Hasil Pendugaan Parameter A dengan MKT dan Metode Bootstrap Residual

Berdasarkan Tabel 3, 4, dan 5 dapat dilihat bahwa penduga parameter yang dihasilkan oleh metode bootstrap residual tidak berbeda jauh dengan penduga parameter yang dihasilkan oleh MKT. Hal ini juga dapat menunjukkan bahwa metode bootstrap residual merupakan penduga yang akurat untuk menduga parameter regresi.

Penduga parameter yang dihasilkan oleh MKT dan bootstrap residual sama-sama menghasilkan penduga parameter yang bias pada data berpencilan 10% dan 15%. Dapat dilihat pada data simulasi dengan nilai Pl = 1 bahwa data dengan pencilan 5% pada selang kepercayaan 95%, penduga parameter yang

dihasilkan menjadi tidak bias pada resampling ke 250 sampai 100.000. Pada data simulasi dengan nilai Pl = 5, data dengan pencilan 5% pada selang kepercayaan 99%, penduga parameter yang dihasilkan oleh bootstrap residual menjadi tidak bias. Hal ini menunjukkan bahwa metode bootstrap residual hanya mampu mengatasi bias pada penduga parameter pada data dengan pencilan sebesar 5%.

Selang kepercayaan yang dihasilkan oleh metode bootstrap residual cenderung stabil. Dapat dilihat pada selang kepercayaan 95% dan 99% yang dihasilkan tidak ada perubahan yang signifikan walaupun telah diresampling sampai 100.000 kali. Hanya saja selang kepercayaan yang dihasilkan metode bootstrap residual memiliki kisaran selang yang lebih lebar dari MKT.

Pada MKT uji kenormalan dilakukan pada sisaan yang dihasilkan oleh model regresi, di dapat kesimpulan bahwa pada data simulasi dengan nilai Pl = 1, Pl = 3, dan Pl = 5, data tanpa pencilan menyebar normal sedangkan data dengan pencilan 5%, 10%, dan 15% tidak menyebar normal. Setelah mengalami proses bootstrap, data simulasi diuji kembali kenormalannya dengan uji Anderson-Darling. Hasil yang didapat tidak berbeda jauh dengan uji kenormalan pada MKT, hanya saja pada data berpencilan 15% pada Pl = 1 dan Pl = 3, data mengikuti sebaran normal. Hal ini dikarenakan sampel yang berasal dari populasi yang menyebar normal, setelah mengalami proses resampling yang terus-menerus dilakukan mengakibatkan asumsi kenormalan pada data terpenuhi.

• 4. SIMPULAN DAN SARAN

Dari hasil yang diperoleh dapat disimpulkan bahwa jumlah pencilan yang hanya 5% dari jumlah data setelah diresampling dengan bootstrap residual mampu menghasilkan penduga parameter dan selang kepercayaan yang mendekati pendugaan awalnya, sehingga penduga yang dihasilkan menjadi tidak bias. Pada penduga parameter

untuk data dengan pencilan 10% dan 15% yang terletak pada gugus bawah data, bias pada penduga parameter tidak dapat teratasi.

Saran yang dapat diberikan pada penelitian ini yaitu pada data simulasi yang digunakan, pencilan dibangkitkan dengan data sisaan, pada penelitian selanjutnya pencilan dapat dibangkitkan pada peubah bebas dan dengan menggunakan analisis regesi linier berganda, regresi logistik, dan analisis regresi lainnya. Pada penelitian ini, bias penduga parameter disebabkan oleh adanya pelanggaran asumsi kenormalan akibat pencilan. Penelitian selanjutnya mengamati bias yang disebabkan pelanggaran asumsi-asumsi lainnya.

DAFTAR PUSTAKA

• [1]    Neter, J., Wasserman, W. & Kutner,

M.H., 1997. Model Linear Terapan Buku

• I:    Analisis Regresi Linear Sederhana.(Terjemahan Bambang Sumantri). 3rd ed. Bandung: Jurusan Statistika FMIPA-IPB.

• [2]    Efron, B. & Tibshirani, R.J., 1993. An Introduction to the Bootstrap. New York: Chapman & Hall , Inc.

• [3]    Sungkono, J., 2013. Resampling Bootstrap pada R. Magistra No.84 Th.XXV Juni 2013, pp.47-54.

137