PERAMALAN KUNJUNGAN WISATAWAN MENGGUNAKAN MODEL ARMAX DENGAN NILAI KURS DAN EKSPOR-IMPOR SEBAGAI FAKTOR EKSOGEN
on
E-Jurnal Matematika Vol. 3 (4), November 2014, pp. 138-145
ISSN: 2303-1751
PERAMALAN KUNJUNGAN WISATAWAN MENGGUNAKAN MODEL ARMAX DENGAN NILAI KURS DAN EKSPOR-IMPOR SEBAGAI FAKTOR EKSOGEN
Putu Ika Oktiyari Laksmi§1, Komang Dharmawan2, Luh Putu Ida Harini3
-
1Jurusan Matematika, Fakultas MIPA - Universitas Udayana [Email: ikaoktiyari@gmail.com]
-
2Jurusan Matematika, Fakultas MIPA - Universitas Udayana [Email: dharmawan.komang@gmail.com]
-
3Jurusan Matematika, Fakultas MIPA - Universitas Udayana [Email: ballidah@gmail.com] §Corresponding Author
ABSTRACT
Forecasting is science to estimate occurrence of the future. This matter can be conducted by entangling intake of past data and place to the next period with a mathematical form. This research aims to estimate the number of foreign tourists visiting Bali models using autoregressive moving average exogenous (ARMAX). The data used in this study is the number of tourists in Australia and the number of tourists in the RRC as a variable Y, and foreign currency exchange rate AUD, Chinese Yuan, and Export Import as the X factor from the period July 2009 to July 2014. In the analysis can be obtained in the best ARMAX models of the number of tourists in Australia is ARMAX(1,2,2) and the best model of the number of tourists in the RRC does not exist because the data for the ARMAX model parameters tourists no significant RRC.
Keywords: forecasting, ARMAX model, and the number tourists.
Penelitian yang akan dilakukan dipilih data Australia dan RRC sebagai objek penelitian menggingat Australia dan RRC adalah dua negara yang penduduknya paling banyak berwisata ke Bali (BPS [2]). Sehingga penulis akan melakukan penelitian tentang memodelkan jumlah wisman yang berkunjung ke Bali dengan model ARMAX dan menambahkan faktor eksogen nilai tukar mata uang asing AUD dan Cina Yuan (CNY) serta faktor eksogen ekspor-impor. Setelah mendapatkan model ARMAX dilakukan peramalan (forecasting).
-
2.1. Definisi Runtun Waktu (Time Series)
Runtun waktu didefinisikan sebagai kumpulan observasi atau amatan yang dibuat secara beruntun (sequentially) atau berurutan sepanjang waktu (Peter & Davis [3]).
-
2.2. Definisi Kestasioneran
Suatu proses stokastik (J7t) disebut stasioner lemah (weakly stasionary) jika mean dari Yt dan kovarians antara γt dan ^t- k bebas dari waktu. Dengan kata lain:
-
(1) z(Yt) = μ yakni mean dari γt bebas dari waktu,
-
(2) Coυ{YtlYt^ = γk yakni kovarians antara Yt dan ^t- k bebas dari waktu untuk masing-masing lag ⅛ [4].
-
2.3. Konsep Kestasioneran
Pada penelitian ini data yang digunakan harus stasioner, karena untuk menghindari hasil regresi palsu. Untuk menstasionerkan data ada dua yaitu dengan melakukan differencing dan uji unit root Augmented Dickey Fuller (ADF). Uji Dickey-Fuller adalah menguji apakah suatu time series merupakan proses random walk atau bukan[5]. Secara umum rumus differencing dapat ditulis sebagai berikut:
Cl-B/, d≥l
Dan untuk rumus ADF secara umum sebagai berikut:
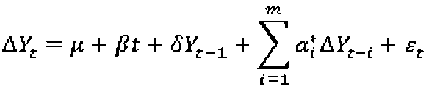
pp
dengan δ = ∑φ - 1 dan ai = -∑φj , st i=1 j=1
adalah komponen error, dan m = p — 1
adalah panjang lag.
-
2.4. Identifikasi Model
Dalam metode time series, untuk mengidentifikasi model dari data yang akan diramalkan adalah dengan menggunakan fungsi Autocorrelation Function (ACF) dan fungsi Partial Autocorrelation Function (PACF). ACF adalah suatu proses yang stasioner baik dalam rata-rata maupun varians[6]. Autokorelasi parsial (PACF) digunakan untuk mengukur keeratan hubungan antar pengamatan suatu time series yaitu zt dan Zt+k(Wei [6]).
-
2.5. Model ARMAX
Salah satu model runtun waktu yang dapat dipandang sebagai perluasan dari model runtun waktu ARMA adalah yang disebut sebagai model ARMAX, yakni model ARMA dengan variabel exogen (Rosadi [7]).
Secara umum, bentuk model
ARMAX(p> q> r'} sebagai berikut: p qr
Zt =∑φpZt-p -∑θqεt-q +∑γrxt-r +εt t =1 t =1 t =1
Dalam prakteknya, koefisien (Φp^q>Yr) diperkirakan dengan metode estimasi maksimum likelihood.
-
2.6. Estimasi Parameter
Dalam estimasi parameter model pada penelitian ini menggunakan metode penduga kemungkinan maksimum (maximum likelihood estimator). Metode kemungkinan maksimum (maximum likelihood estimator) merupakan suatu metode yang mengarah ke penduga yang memiliki sifat sampel besar.
Misal mempunyai n pengamatan adalah
^ I^ 2 xn yang masing-masing mempunyai suatu pdf f(xi>^. Fungsi likelihood adalah
suatu fungsi dari G yaitu
i ce)=f (.χ1, &)... f{xn, θ)=y^f(,xi,θ). i=l
Jika 0 adalah anggota suatu selang terbuka dan C^ terdiferensial dan mempunyai
suatu nilai maksimum pada selang tersebut, maka MLE adalah suatu penyelesaian dari persamaan maksimum likelihood
= 0
Beberapa nilai dari θ yang memaksimumkan ^®) juga akan memaksimumkan log likelihood i(⅛, maka untuk perhitungan yang cepat, sebagai bentuk alternatif dari persamaan maksimum likelihood adalah
-Iogl(G) = O as
-
2.7. Uji Kenormalan Residual
Uji normalitas residual metode OLS secara formal dapat dideteksi dari metode yang dikembangkan oleh Jarque-Bera (J-B).
Uji statistik dari JB ini menggunakan perhitungan skwenes atau kepencongan dan kurtosis. Adapun rumus uji statistk JB adalah sebagai berikut:
s2 (K-3)2'
JB = n — + -----— j
6 Ξ4
-
2.8. Definisi Peramalan
Definisi peramalan adalah memperkirakan besarnya atau jumlah sesuatu pada waktu yang akan datang berdasarkan data pada masa lampau yang dianalisis secara ilmiah khususnya menggunakan metode statistika (Sudjana [8]).
Keakuratan peramalan dapat menggunakan rumus, nilai tengah kesalahan kuadrat atau Mean Square Error (MSE) yaitu
m Sc —-----—----------
n n
Dan Tingkat kesalahan peramalan rata-rata atau Average Forecasting Error Rate (AFER) yaitu yn ⅛→k∣ ⅛=ι X
AFER =-------5--(100%)j n
Dengan mencari nilai MSE dan AFER yang minimum (Bowerman & Koehler [9]).
dan PACF; (4) Melakukan estimasi dan uji signifikansi parameter model ARMAX(p, q,r) dengan uji maximum likelihood estimator; (5) Melakukan diagnostic checking, yang meliputi uji residual white noise dengan uji Ljung-Box; (6) Melakukan seleksi model untuk menentukan model terbaik dengan menghitung nilai AIC dan BIC; (7) Setelah mendapatkan model terbaik maka akan dilakukan peramalan jumlah wisman yang berkunjung ke Bali dengan melihat keakuratan peramalan dengan nilai MSE dan AFER yang minimum.
-
A. Hasil Penelitian dengan Model ARMAX
Pada mencari model terbaik dari model ARMAX dapat dilakukan dengan langkah-langkah sebagai berikut: melakukan plot data, selanjutnya menguji kestasioneran data, menentukan orde ARMAX, melakukan estimasi parameter dari model ARMAX dengan uji maximum likelihood estimator, melakukan diagnostic checking, mencari model terbaik dari nilai AIC dan BIC yang minimum, dan melakukan peramalan.
A.1 Plot Data
Plot data dilakukan secara visual untuk melihat adanya tren, komponen musiman, stasioner, non-stasioner dalam variansi. Plot data deret waktu pada jumlah wisman Australia dan RRC serta kurs AUD dan kurs CNY dan ekspor-impor dapat dilihat dari plot series atau grafik. Sebagai contoh dilakukan plot data jumlah wisman.
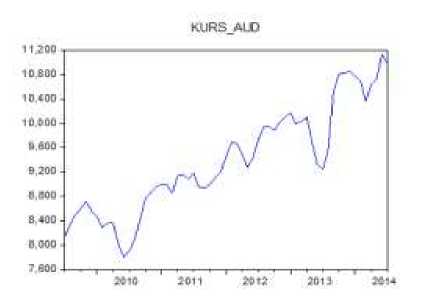
Gambar 1. Plot data wisman Australia
Berdasarkan hasil plot data jumlah wisman dari Gambar 1. di dapat jumlah wisman Australia tidak stasioner dalam mean karena adanya tren naik. Tren naik ditandai dengan adanya bentuk kenaikan data dalam perubahan waktu. Dan adanya pengaruh musiman ditandainya ada pengulangan data setiap tahun.
Dari plot data jumlah wisman Australia mengalami pasang surut sepanjang bulan Juli 2009 sampai Juli 2014, namun jumlah wisman Australia yang tertinggi terjadi pada bulan Juli 2014 sebesar 94.605 dan jumlah wisman Australia yang terendah terjadi pada bulan Februari 2010 sebesar 33.559.
A.2 Uji Stasioner Data
Setelah melakukan plot data, terlihat data tidak stasioner karena adanya tren naik dan musiman (seasonal) pada data. Maka dilakukan uji stasioner data untuk menghindari hasil regresi palsu. Untuk melihat kestasioneran data dapat dilihat melalui plot ACF dan PACF, sebagai contoh dilakukan pada data jumlah wisman Australia.

Gambar 2. Plot ACF dan PACF
Berdasarkan korelogram ACF dan PACF pada Gambar 2 data jumlah wisman Australia tidak stasioner, karena terlihat bahwa plot autokorelasi berada diluar garis Bartlett (garis putus-putus) dan nilai probabilitas yang lebih kecil dari 5% (0.05) yang berarti terima ^l yang menunjukan bahwa data jumlah wisman Australia tidak stasioner . karena data tidak stasioner maka data di differencing menggunakan persamaan
^Z t - Zt ^t-‰
(1)
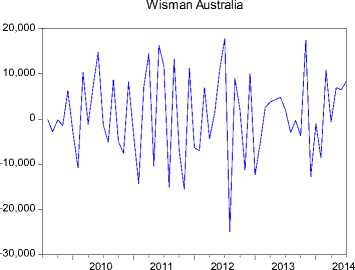
Gambar 3. Plot differencig
Plot data wisman yang telah stasioner pada Gambar 3 dapat dilihat sudah stasioner karena meannya bernilai diantara nol.
Selain menggunakan differencing untuk melihat stasioneran data, dapat juga dilakukan dengan uji unit root ADF( augmented Dickey Fuller) dengan persamaan m
ΔFt = μ + /?t + ¾.1 + V α*ΔKt^ + ⅛
i=l (2)
Tabel 1. Uji Uji Kestasioneran Variabel Pada Level
|
Hj |
Yarstd |
AEf |
⅛tta≡n |
JtatetdKS |
Eerxtfin |
|
1. |
Wianan AUD |
4,42233 |
•3,436509 |
0,0040 |
Sssmr |
|
γA,i≡3 RRC |
■5,662165 |
-3,436509 |
0,0001 |
Ssscter | |
|
j. |
Ers AUE1 |
4.54DS82 |
-3,437345 |
0,0030 |
Sssmer |
|
4 |
EjxsCNY |
-5,MP4? |
-3,437345 |
0,0006 |
Sssmer |
|
Ekspor |
4 64327 |
■1910860 |
0.0004 |
Sssmer | |
|
6 |
tata |
-9925051 |
-1910860 |
0.0000 |
Sssizter |
Terlihat dari Tabel 1 bahwa nilai statistik uji ADF data wisman Australia sebesar -4.442233 yang lebih kecil dari nilai kritis £1 = 0.05, sehingga hipotesis nol ditolak, atau data differensi dari data wisman Australia sudah stasioner ( tidak mengandung unit root). Karena semua variabel sudah stasioner maka tahap selanjutnya menentukan orde ARMAX dengan uji ACF dan PACF.
A.3 Menentukan Orde ARMAX(p, q,r)
Setelah semua variabel wisman Australia, wisman RRC, Kurs AUD, dan Kurs CNY stasioner. Selanjutnya dilakukan penentuan orde ARMAX, dengan cara melihat
plot ACF dan PACF dengan persamaan
_rk -Σ‰⅞-Γ)(⅛-z)
Pk r0 ∑j=i(zt-z)2 (3)
_ Pk - ∑J=1 Φk-l,]Pk-j φkk~ i-p-ι⅛ o
1 ⅛-=ι Ψk-ι,jPj (4)
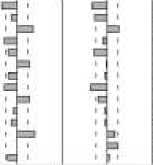
Plot ACF dan PACF dapat dilihat pada
Gambar 4.
DQlv WW14 TWTH «1» 8∏μ∣ JMMIHM’W HtXiaadreiamMuii W
WficuiiMatm fmm CiaraMloi AC FaC O-SLal Fios
1 -fl 347 -0 347 7 WtG OOW 2 -OTM -0»» BTOJ QGIJ 3 03B 0264 17 M2 C CO) 4 -OZtBJ -OOM 7) ID OdOO β 0»K 8 3« HMi OQOO a QMT -OOD D IAt OOOJ 7 82M 4 0« 34191 0 0« a 82*3 -0 372 30*34 QOW 9 02W -O »9*5 *»049 OOW
IQ OOM OKI M‘21 QOW 11 -Q 123 -O QAO 47 ∏3 Q OW 12 0 421 OHO 81484 COW 13 -OOM 0 254 614M OCW 14 0 207 OOW MM7 GOW
Gambar 4. Plot ACF dan PACF
Dilihat dari plot ACF dan PACF data hasil diffrencing pada Gambar 4 tampak bahwa terdapat pola musiman, tetapi pada penelitian ini lebih menekankan pada model ARMAX. Dari analisis plot data ACF terpotong pada lag (1,3) dan plot PACF terpotong pada lag (1,2). Untuk memodelkan data menurut parsimony (kesederhanaan) dari model (yakni model yang baik adalah model yang memiliki parameter yang sedikit), sehingga didapatkan kandidat model ARMA C1'1), ARMA (1,Ξ), ARMA C2'1), dan ARMA (2,ξ). Dan untuk orde ARMAX dimasukan faktor eksogen kurs AUD dan ekspor. Berarti model ARMAX (U,2), ARMAX (½2), ARMAX (2j1^ dan ARMAX (2,2,2).
Begitu juga untuk plot ACF dan PACF untuk jumlah wisman RRC (Gambar 5).
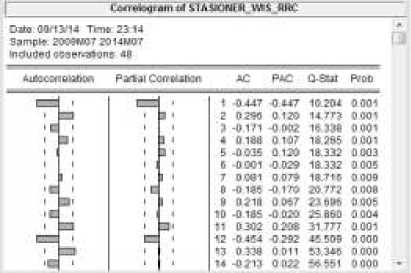
Gambar 5. Plot ACF dan PACF Jumlah
Wisman RRC
Untuk data wisman RRC tidak jauh berbeda dari penjelasan data wisman Australia. Berdasarkan plot ACF dan PACF pada Gambar 5 dapat dilihat plot ACF terpotong pada lag (1,2) dan plot PACF terpotong pada lag (1). Sehingga model ARMA yang didapat ARMA(i,i), ARMAC1'2), ARMAC2'1) dan ARMAC2'2). Seperti halnya pada data wisman
Australia, data wisman RRC juga terdapat pengaruh musiman juga, tetapi karena pada penelitian ini lebih menekankan model ARMAX maka didapatkan model ARMAX dengan faktor eksogen kurs CNY dan data impor. Jadi model ARMAX yang didapat ARMAX (U,2), ARMAX (½2), ARMAX (2,1,2) dan ARMAX (2,2,2).
A.4 Melakukan Estimasi Parameter Model
ARMAX(p, Qfr)
Berdasarkan plot ACF dan PACF didapat orde untuk estimasi model ARMAX. Akan dilakukan estimasi parameter untuk model wisman Australia ARMAX(1,1,2)
Deoendent Vanaole Lisman Australia IJetnc-O LeastSquaaes
Dale 1OΛ6rl4 Time 21 50
Samtχe(adιusteσ) 2OO9<1O9 2014M07
Jnauded ODserrakons 59 alter aφusimenu Corrvergence achieved aΛef 17 iterations UA Backeast 2009U08
|
VartatMe |
Coefficient |
SSd E nor |
Pros | |
|
C |
823 2827 |
267 486 7 |
3 077848 |
0 0033 |
|
DkURS AUD |
-4 390337 |
4 671138 |
-O 939886 |
O 3515 |
|
DEKSPCR |
0 000241 |
0 000143 |
1 68 58 3 3 |
0 0976 |
|
AR(I) |
0 467474 |
O 129948 |
3 597 399 |
0 0007 |
|
UAiIJ |
-0 954118 |
0 023419 |
-41 15824 |
OOOOO |
|
Rsquared |
0 281882 |
Mean dependent war |
834 1525 | |
|
Adjusted Rsquared |
0 2 28589 |
S O dependent ear |
9464 496 | |
|
SE ofreg∣essιon |
8312131 |
Akaire indo entenon |
20 96976 | |
|
Sum squared resid |
3 7 3E→9 |
ScfiMrarc cπtendn |
21 14582 | |
|
Log McekhOdd |
-613 6079 |
Hannan Qumn enter |
21 03849 | |
|
F statute |
5299151 |
DuroinAVatson stat |
2 039176 | |
|
ProtnF 3*3tlS⅛C I |
0001128 | |||
|
Gambar 6. Estimasi Model | ||||
Hasil uji ditunjukan oleh Gambar 6 didapat nilai parameter konstanta dengan Prob = 0,0033 < 0,05, maka j^Q ditolak yang berarti bahwa konstanta signifikan dalam model ARMAX(1,1,2). Untuk uji parameter AR(1) didapat nilai Prob = 0,0007 < 0,05, maka ^r∣) ditolak yang berarti bahwa AR(ι) signifikan dalam model ARMAX(1,1,2). Selanjutnya akan diuji untuk parameter MA(!) dengan nilai prob = 0,0000 < 0,05, maka j^Q ditolak yang bearti MA(!) signifikan dalam model
ARMAXCU,O. Begitu juga akan diuji untuk parameter kurs AUD dengan nilai prob= 0,3515 > 0,05, maka j^∣J diterima yang berarti kurs AUD tidak signifikan dalam model ARMAX(1,1,2). Uji parameter untuk ekspor dengan nilai prob = 0,0976 > 0,05, maka ^∣Jditerima yang berarti ekspor tidak signifikan dalam model ARMAX(1,1,2).
Oeperoefrt vanaNe «sman RRC
Uelhod Leis? Souares
Date 1006-14 Time 23 03
Swπ0β busied 2009M09 2014M07
IACJoded WitMtoflS 59 MK Jd1Ul-VnKrtl
Cccr.eιgfrnct achieved Mw 3 Heratons UA Sacrtast 2O09M08
|
VanaNe |
CoeOoent |
SM Enw |
I-SUHto |
Prob |
|
C |
0 031503 |
0 057434 |
0 548-15 |
0 5356 |
|
OKURS.CNY |
OOOOSV |
0 001576 |
05373« |
05933 |
|
UPOR |
-SiJE-IO |
1036-« |
•0 594202 |
05549 |
|
*R(1) |
OOMSOO |
2159323 |
0000116 |
09999 |
|
IW(I) |
0 002500 |
2155917 |
0 000116 |
09999 |
|
R-Sduired |
0 008591 |
Utan MptflOtfttvar |
0 021031 | |
|
A⅜>⅛<> R-PduarK |
∙0W4W7 |
SO Oecendertrar |
O 362732 | |
|
SE OfiKTHMO |
O 3 7 4 33 8 |
Mtaut ices Cflttnon |
0 953465 | |
|
Sum squared resid |
7 565769 |
Scheanoteoon |
1 129528 | |
|
109 IilCHhOOd |
-23 12722 |
Hannah-Qunfl enter |
1022193 | |
|
F-Stttstc |
0116931 |
Ourtrn-AatSDn stat |
2521669 | |
|
Pto&J-staHto) |
0 975940 | |||
Gambar 7. Estimasi Parameter
Hasil uji ditunjukkan oleh Gambar 4.11 didapat nilai parameter konstanta dengan Prob = 0,5856 > 0,05, maka JZa diterima yang berarti bahwa konstanta tidak signifikan dalam model ARMAXCU⅛ Untuk uji parameter AR(ι) didapat nilai Prob = 0,9999 > 0,05, maka Ha diterima yang berarti bahwa ARCO tidak signifikan dalam model ARMAXCU⅛ Selanjutnya akan diuji untuk parameter MACO dengan nilai prob = 0,9999 > 0,05, maka Ha diterima yang bearti MAco tidak signifikan dalam model ARMAXCu⅛ Begitu juga akan diuji untuk parameter kurs CNY dengan nilai prob = 0,5933 > 0,05, maka H ∣J diterima yang berarti kurs CNY tidak signifikan dan data impor dengan nilai Prob = 0,5549 > 0,05, maka J/ ∣J diterima berarti data impor tidak signifikan pada model ARMAXCU⅛
A.5 Melakukan Diagnostic Checking
Untuk melakukan diagnostic checking, selain menggunakan kriteria uji t untuk parameter atau koefisien hasil estimasi, maka
analisis selanjutnya adalah dengan melakukan uji Q-Ljung-Box dan plot ACF dan PACF. Asumsi-asumsi yang diperlukan dalam analisis runtun waktu sebagai berikut:
-
a. Tidak ada autokorelasi dalam residual,
-
b. Model bersifat homoskedastisitas (variabel residual konstan),
-
c. Residual bersifat normal.
Uji asumsi untuk jumlah wisman Australia di ringkas dalam Tabel 2.
Tabel 2. Perbandingan Model Wisman Australia Berdasarkan Asumsi
|
Modd |
NotAutokonias |
Hoπκiħdastisias |
NonnaHas |
|
ARMAX Ci, W |
Terpaiihi |
Terpauhi |
T≡tfeιu±: |
|
ARMAX (U2t |
Terpauhi |
Terpauhi |
Terpenuhi |
|
ARMAX (2,L2) |
Terpauhi |
Terpauhi |
TapentL |
|
ARMAX (2,2,2) |
Terpauhi |
Tiiak Urpeaiu |
TapenitL |
Berdasarkan Tabel 2 didapat semua model ARMAX dari data wisman Australia memenuhi asumsi uji diagnostic checking.
Selanjutnya dilakukan uji asumsi untuk jumlah wisman RRC. Dapat dilihat pada Tabel 3 dibawah ini,
Tabel 3. Perbandingan Model Wisman RRC Berdasarkan Asumsi
|
Modd |
NunAutokcrdasi |
Homtikedsstisxas |
NomEHas |
|
ARMAX (LL2) |
T etpeπuL |
Tidak Terpauhi |
TapenuL |
|
ARMAX (L2Λ |
Tapewii |
Tifet Terpauhi |
TapenuL |
|
ARMAX (2. U) |
Tapeniuti |
Tidak Terpaiihi |
TapenuL |
|
ARMAX (2,2,2) |
T etpenuL |
Tidak Terpaiihi |
TapenuL |
Berdasarkan Tabel 3 didapat semua model ARMAX data wisman RRC memenuhi asumsi nonautokorelasi dan asumsi normalitas.
A.6 Pemilihan Model Terbaik
Dari estimasi model sementara yaitu model wisman Australia dan wisman RRC baik digunakan untuk memprediksi model selanjutnya karena dalam uji diagnostic checking semua asumsi terpenuhi.
Pemilihan model terbaik dapat dilihat dalam Tabel 4 untuk jumlah wisman Australia.
Tabel 4. Perbandingan Model Berdasarkan Kebaikan Model Wisman Australia
|
ARMAX(LU) |
ARMAXiUJO |
ARMAXiJ.lJI |
ARMAX(JJi) | |
|
823.2827 (0,0033) |
0.015831 (0.0133) |
PPMlW (0.155 J) |
1046.125 (OJ 503) | |
|
4I |
0,4674 74 01.0007) |
0,4 WHO (0.0036) |
- | |
|
«1 |
-0.03628 7 (D1SlOSj |
0.513927 IO1DSSfi | ||
|
*1 |
-OW i 18 (0.0000) |
-0,41(700 (0,0043) |
- | |
|
O1SSfTTD (0.0000) |
•0.7MJ» (0,00025) | |||
|
A |
^,1MJΠ (B,3515) |
-SJtE-OJ (0.15W> |
-4,126668 (0.3507) |
-5,32769? (O1JtlO) |
|
T1 |
0.0002«! (0,0976) |
X74E-O0 (0.2537) |
0.00016(1 (0,2682) |
0.000316 (O1MM) |
|
i» |
JJJEiO? |
0.960333 |
4J6E*O9 |
4.45EMB |
|
AiC |
JOJtm |
-I.I1OM4 |
JLOtMO |
21.1*605 |
|
NC |
21.14582 |
OJMMJ |
21.2761)3 |
21.34567 |
Dengan demikian terlihat bahwa model ARMAX(1,2,2) merupakan model terbaik untuk data jumlah wisman Australia karena uji koefisien signifikan dan semua asumsi untuk uji residual terpenuhi dan memiliki nilai AIC dan BIC minimum sebesar -1,110644 dan -0,934582.
Untuk model wisman RRC perbandingan model terbaiknya diringkas pada Tabel 5 sebagai berikut:
Tabel 5. Perbandingan Model Berdasarkan Kebaikan Model Wisman RRC
|
ARMAX(LU) |
ARMAX(Lli) |
AFtnmiT; |
AJtMAXiJJJ) | |
|
C |
0,031503 (0.5856) |
0,0)15(71 (0.5840) |
0.021198 (0,5935) |
0,031298 (0,5933) |
|
0.00 2500 (O4PPW) |
O1OOBOO (O1Mtt) | |||
|
«f |
0.001500 (0,9867) |
0,002500 (0,9999ι | ||
|
93 |
0.00 2500 (O1PPPP) |
0,001500 (0,9867) | ||
|
»« |
O1CVJSriC 10,9865) |
0,002500 (0,9999ι | ||
|
⅝ |
0.00084 7 (0.5933) |
0,004? (0,5976) |
0,000850 (0,6004) |
0,000850 (0,5966) |
|
-6.12E-JD (0.5549) |
-6,l4E∙iO <0,55M) |
-4.1 SE-LO (0,5568) |
-6,17E∙IO {0.555Ii | |
|
JSW |
7.565749 |
7.560545 |
7,560410 |
7,555421 |
|
NC |
0,05 3465 |
O1K 2774 |
0,972773 |
0,972113 |
|
BJC |
1.129528 |
I.IW3J7 |
1.150393 |
1.149733 |
Dengan demikian terlihat bahwa model ARMAX untuk data wisman RRC tidak ada yang signifikan, berarti untuk model ARMAX data wisman RRC tidak ada.
A.7 Melakukan Peramalan
Langkah terakhir dalam analisis runtun waktu adalah menentukan peramalan atau proyeksi untuk periode selanjutnya. Dalam
pembahasan ini akan diproyeksi rata-rata jumlah wisman untuk 12 periode kedepan dan hasil peramalannya, dapat dilihat pada Tabel 6.
Tabel 6. Hasil Peramalan Model ARMAX
(1,2,2) Untuk Data Wisman Australia.
|
PeriCGi Sekanna; |
EiiL Psfamalzi |
Data Penode Sebemmrrra |
Itsi dual |
⅛eadual |
|
.∙⅛BS∏h 2014 |
91830.43 |
71701 |
20129,43 |
3,29 |
|
Swsnibe 2014 |
92861.40 |
71408 |
21453,4 |
3.51 |
|
Ofcobe 2014 |
93903,95 |
67680 |
26223 95 |
4,29 |
|
Xcvanter 2014 |
94958.21 |
85151 |
9807.21 |
1.60 |
|
Dssembe 2014 |
9602433 |
72336 |
23688.3 |
3.88 |
|
Jinnari 2015 |
9710236 |
71288 |
25814,36 |
4,23 |
|
Februan 2015 |
98192,52 |
62678 |
35514,52 |
5,82 |
|
Mret 2015 |
99294,92 |
73509 |
25785,92 |
4 |
|
April 2015 |
100409.7 |
72831 |
27578.7 |
4.52 |
|
.Mei 2015 |
101537,0 |
79808 |
21729 |
3,56 |
|
Jua 2015 |
102676,9 |
86292 |
16384,9 |
2,68 |
|
Joli 2015 |
103829,7 |
94605 |
9224,7 |
1,51 |
|
AFFF. |
0,76 | |||
|
MSE |
104743032,1 |
Dari nilai hasil peramalan pada Tabel 4.6 dapat disimpulkan bahwa dari hasil analisis menggunakan model runtun waktu ARMAXC½Ξ) ini peramalan yang dihasilkan mengalami kenaikan untuk 12 periode ke depan. Dari bulan Agustus 2014 sampai bulan Juli 2015 dengan nilai AFER sebesar 7,06 persen. Untuk plot data setelah dilakukan peramlan selama 12 periode ke depan yaitu
110,000
100,000
90,000
80,000
70,000
60,000
50,000
40,000
30,000
wisman Australia
2010 2011 2012 2013 2014 2015
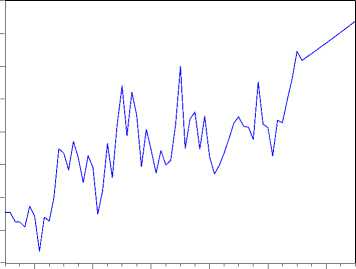
Gambar 8. Plot Setelah Peramalan
Dari Gambar 8 setelah melakukan peramalan dari model ARMAX(1,2,2) didapat terjadi peningkatan jumlah penumpang dari bulan Agustus 2014 sampai bulan juli 2015.
Selanjutnya peramalan model ARMAX untuk data RRC tidak ada, karena tidak terdapat koefisien parameter dari model ARMAX RRC
yang signifikan. Jadi tidak dapat dilakukan proses peramalan untuk model ARMAX untuk wisman RRC.
Berdasarkan hasil dan pembahasan yang telah diuraikan pada bab sebelumnya, maka diperoleh simpulan sebagai berikut:
-
1. Model peramalan ARMAX untuk data wisman Australia di dapatkan model ARMAX(W). Model ARMAX(W) dipilih berdasarkan nilai AIC dan BIC yang paling minimum diantara model ARMAX yang lai. Dan untuk model ARMAX data wisman RRC tidak ada, karena koefisien parameter untuk model ARMAX wisman RRC tidak ada yang signifikan.
-
2. Hasil peramalan yang didapat dari model ARMAX(W) untuk wisman Australia, terjadi peningkatan jumlah wisman dari bulan Agustus 2014 sampai bulan Juli 2015 untuk model ARMAX(W) dengan nilai AFER sebesar 0,76 dan nilai MSE sebesar 104743032,1.
Untuk penelitian selanjutnya dapat menggunakan variabel yang lain seperti variabel yang memengaruhi kedatangan wisatawan ke Bali selain variabel kurs dan ekspor-impor dengan menggunakan model ARMAX.
DAFTAR PUSTAKA
-
[1] Makridakis, S., Wheelwright, S. C., & McGee, V. E. 1999. Metode Aplikasi Peramalan.2nd ed. Tanggerang : Binarupa Aksara.
-
[2] Badan Pusat Statistika. 2007. Perkembangan Pariwisata Bali Januari 2007 .1st ed. Denpasar: Badan Pusat Statistika Provinsi Bali.
-
[3] Peter, B. J., & Davis, A. R. 2002. Introduction to Time Series and Forecasting. New York: Springer
-
[4] Tsay, R. 2002. Analysis of Financial Time Series. (W. John, & I. Sons, Eds.) New York: Finansial Econometrics.
-
[5] Widarjono, A. P. 2013. Ekonometrika Pengantar dan Aplikasinya. Yogyakarta: UPPT STIM YKPN.
-
[6] Wei, W. W.S.2006. Time Series Analysis: Univariate and Multivariate Methods. 2nd ed.. New Jersey: Pearson Prentice Hall.
-
[7] Rosadi, D. 2011. Ekonometrika & Analisis Runtun Waktu Terapan . Yogyakarta: Andi.
-
[8] Sudjana. 1986. Metode Statistika . Bandung: Tarsito.
-
[9] Bowerman, o'connel, & Koehler. 2005. Forecasting Time Series and Regression An Aplied Approach. United States of Amerika.
145
Discussion and feedback