SOME NEW RESULTS OF A FRACTIONAL VON BERTALANFFY MODEL

E-Jurnal Matematika Vol. 12(3), Agustus 2023, pp. 194-199

DOI: https://doi.org/10.24843/MTK.2023.v12.i03.p419

ISSN: 2303-1751

SOME NEW RESULTS OF A FRACTIONAL VON BERTALANFFY MODEL

Avan Al-Saffar^1§

¹Department of statistics, Collage of Administration & Economics, University of Duhok, Iraq [[email protected]]

^§Corresponding Author

ABSTRACT

In this article, we review the deterministic and perturbed Von Bertalanffy model that has been developing to discuss the existence and uniqueness results of the model. The key research issues are highlighted, and the results and interpretations are summarized. We investigate the effects of changing some of the system's control parameters through numerical simulations. We resolve the Von Bertalanffy ordinary differential equation of fractional order. The analytical solution is obtained.

Keywords:  Ordinary differential equation, periodic fluctuations, growth model, fractional

derivative, existance and uniqueness.

1. INTRODUCTION

In 1838, Von Bertalanffy presented the Von Bertalanffy model as an organism growth model. This model demonstrates how the tumor's volume changes in relation to the surface area and with cell death. This model, in Vaidya's opinion, accurately forecasts the progression of human tumors (Vaidya (1982)). The Von Bertalanffy ordinary differential equation is written as follows:

dv

— = K (L∞-v)       (1)

dt

where t is time, v is length (or some other measure of size), K is the growth rate and L∞, termed 'L infinity' in fisheries science, is the asymptotic length at which growth is zero.

The solution, for a given initial condition v(0) = v₀, is:

v(t) = L∞- (L∞ - vo)e^-κt        (2)

Eq. (1) presents a sigmoidal curve for v(t) and can model human's height and mass, a fish community, a rabbit (see Zwietering (1990); Waliszewski (2003) and references therein), diverse malicious tumors (Laird (1964); Laird (1965)). For processing biological systems and researching ecology, the traditional Von Bertalanffy system is helpful.

Research has been done to convert deterministic growth models to their stochastic counterparts because deterministic models are in fact insufficient to explain the dynamical process of population expansion (Shabana (2019) and references therein). Researchers have expanded the Von Bertalanffy model in numerous investigations (Lee (2020); Garcia (1983); Konig (2019)). On the other hand, the only models that have been extended to their stochastic counterpart to date are the logistic and Gompertz models (Shabana (2019) and references therein); Al-Saffar (2017); Al-Saffar (2020)).

By changing the most important parameters that reflect the presence of noisy behavior, deterministic models can be converted into their stochastic equivalent. The intrinsic growth rate parameter K is perturbed so that the mathematical model in the form of stochastic Von Bertalanffy emerge.

A modulation in the model parameters is examined using fractional derivatives. The fractional operators are increasingly taken into account in biological system modeling due to its interesting advantages in analyzing complex evolution and behaviour patterns linked to memory or fractals. (Wang (2009); Ahmed (2007); Kilicman (2018); Ishak (2022); Ishak

(2023)). There have been many revisions and modifications of the Von Bertalanffy equation (1) discussed, but it is difficult to see a fractional version of this differential equation.

The system in Eq. (1) has one steady state v* = L_m. v can represent the population of any species of interest (e.g. tumor, rabbit, bacteria, etc). For a constant K > 0,v reaches L_m as t → ∞ regardless of the initial value of v(t = 0) = v₀. Finding the numerical and analytical answer to Equation (1) is convenient. One intriguing feature of the Von Bertalanffy equation is that the population will display an equilibrium solution at v = L_m, as we can see from Fig. (1) which is a constant, unchanging point in time. As a result, the population will stop growing, unlike how it would if K or v were 0. This illustrates that the partial derivative with respect to time is equal to zero for a variety of initial conditions. ^^ = 0∙

For the model in (2), where v₀ is the initial value of v at (t = 0). We show the typical time history of v(t) for different values of ω and v₀ in Fig. (1).

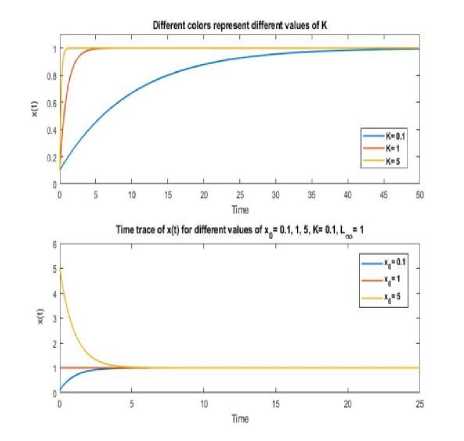
For L_m = 1, v₀ = 0.1, the upper panel from figure (1), it is obvious that the solution show a stable grow at L_m = 1 for different values of the parameter growth K with only a difference which is the time that the system spent as an initial transient, also, this indicates that for higher values of K, the length (or any other sizemeasure) of the organism will reach the asymptotic length faster which leads the population to stop expanding early. Whereas in the lower panel where we fix the value of K and change the initial condition, we observe a similar behaviour.

2.

VON BERTALANFFY MODEL WITH A PERIODIC MODEULATION

Different growth populations have been frequently modeled using deterministic Von Bertalanffy models. By modulating the growth rate parameter K, the Von Bertalanffy equation with periodic modulation is formed as follows:

dv

— = (a + β cos ω t) (L_m — v) at

(3)

In the case of a periodic fluctuation (a + β cos(ωt)) is included in the growth rate parameter, where a is a constant growth, β and ω are the amplitude and frequency of the modulation, respectively. The analytical solution to Eq. (3) can be found in the following form:

v(t) = Lm- (Lm — v0)e^-at-⅛ ^sin(^{ω t})    (4)

where v₀ represents v’s initial value at t = 0. The perturbed model is appropriate for providing study of the growth of populations and expansion.

• 3.    PRELIMINARIES

We present these preliminary results in order to explore the presence and uniqueness of the initial value solution for the the following fractional representation of the Von Bertalanffy differential equation has been taken into consideration.

• ^cD^pv(t) = (a + β cos(ω t)) (L_m — v) (5) with p ∈ (0,1) and D^p represents the Caputo fractional derivative, with v(0) = 0, Where

• ^cD^p, denotes the Caputo differential operator of order p,0 < p < 1,a, β, ω, L_m are parameters, t ∈ [0,T]. Let's review some fundamental definitions of fractional calculus that will be useful for this study.

Definition 3.1. (Agarwal, (2011)

The Caputo derivative of fractional order p is defined as follows for a continuous function g: [0,∞) → ft:

• 1    (^t

^CDP(t)= _l^ pβ(

• — sΓ^-p-' g^ι (s)ds,

n — 1 < p < n,n = [p] + 1, where the integer component of the real number p is denoted by [p].

Definition 3.2. (Ishak, (2020)) The Riemann-

Liouville fractional integral of order p is defined

by

Fftf) =

1 C^t

—fi^ — sy^-1^,

p > 0

Proof. Let A ⊂ Θ be bounded, then ∀ t ∈ [0,T],v ∈ A, there exists a positive constants ξ₁,ξ₂ such that |v(t)| ≤ ξ₁ and | cos(ω s) ≤ ξ₂, thus, we have:

|(n v)(t)|≤

assuming the integral is available.

1 t τ<pd^(f-s)p-1|

+ β cos(ωt))(L_m

a

— v)|ds

Theorem 3.1. (Ishak, (2020)).

Assuming that x is a Banach space, Ω is an open bounded subset of x with θ ∈ Ω, and T: Ω → x is a fully continuous operator, then the following conditions hold:

||Tu|| ≤ |u||,   ∀ u ∈ ∂Ω

Then T has a fixed point in Ω.  □

Lemma 3.1. (Ahmad (2011))

For p > 0, the universal solution of the fractional differential equation is ^c D^pv(t) = 0, is donated by:

v(t) = c₀ + c₁t + —+ c_n-1t^n-1 where c_i ∈ R,i = 1,2, ∙ n — 1, n = [p] + 1.

□

The following can be derived from lemma (3.1): l^pcD^pv(t) = v(t) + c₀ + c₁t + c₂t² + ∙∙∙

+ c_n-1t^n-1

for some c_l ∈ R,i = 1,2,∙∙∙n — 1.

Rewrite the problem (5) as:

1 ^tt

v⁽t) = —— I ⁽t — s)^p-1ρ(t, v(t))ds, v⁽0) ^r(P)Jo

=0

where

ρ(t,v(t)) = (a + β cos(ω t)) (L∞ — v), and ρ(a, β, ω, t, L∞, v(t)) = (a +

β cos(ω t)) (L∞ — v)

1   ^,t

≤^∖ (t — s)^p-¹(|aL_∞| ^r(p) 0q

— a|v(s)|

+ βL∞ cos(ωs) |

— β| cos(ωs)||v(s)|)ds

4. EXISTENCE RESULTS

Let Θ = C([0,T],R) stands for the Banach space of all continuous functions from [0,T] → R endowed with the norm defined by:

||v|| = sup∣v(t)∣,t ∈ [0,T]

Define an operator Π: Θ → Θ as:

(Πv)(t) =

1 C^l

Γ(P) J₀ ^{(t - s}^^p-1ρ(^{s, v(s))ds},

Observe that the operator Π must have a fixed point in order for the equation in (5) to have a solution.

Lemma 4.1.

The operator Π: Θ → Θ is completely continuous.

^aL∞

_—

aξ1 + βL∞ξ2

Γ(p)

—

_—

s) ¹ ds

βξξfi^,(t

0

(aL_∞—aξ1 + βL_∞ξ2—βξ1ξ2t^p

“           Γ(p + 1)

This suggests that |(n v)(t)| is limited, furthermore, for t₁, t₂ ∈[0,T],we have

|(Πv)(t2) — (∏v)(t1)|

1    f^t2

≤w)∖₀ ^(t2

— s)^p-1|ρ(s, v(s))|ds

^aL∞

—

—

1

Γ(p)

∖∖t1 0

— sf^{p 1}|ρ(s, v(s))|ds

aξ1+βL∞ξ2

Γ(p)

—

—

βξ1ξ2

s)'^{p 1}ds

— ∫^t(t1 0

_—

s)^{p 1}ds]

_< (aL∞ — aξ1 + βL∞ξ2 — βξ1ξ2)(tP — tP)

Γ(p + 1)

The Ascoli-Arzela theorem states that Π: Θ → Θ is entirely continuous since the right-hand side of the inequality above goes to zero regardless of

v ∈ Θ as t₂ → t₁.

Theorem 4.1.

Let

ρ(a, β, ω, t, L∞, v(t)): [0, ∞] × [0, ∞] × [0, ∞] × [0, T]×[0,∞]×R → R

and

_ι ρ(a,β,ω,t,L∞,v(t)) _n

lιm-------------------= 0

v→0         v

then problem (5) has at least one solution.

Proof. Since

_ι ρ(a,β,ω,t,L∞,v(t)} _n

lim-------------------= 0

v→0         V

2t^pM r >-------

^ Γ(p + 1)

then there exists a constant e > 0 such that ∣ρ(a, β, ω, t, L∞, v(t))∣ ≤ μ∣v∣ for 0 < |v| < e where μ> 0 and

t^p

Γ(p + 1∕≤¹

Define B = v ∈ Θ: ∣∣v∣∣ < e and take v ∈ Θ such that ||v|| ⊂ e that is v ∈ ∂B by Lemma (4.1), we know that Π is completely continuous and

we show that ΠB_r ⊂ B_r where B_r = v ∈ C[0,T]: ∣∣v∣∣ ≤ r, for v ∈ B, we have:

∣(∏v)(t)∣

≤ max [ I

0

^t (t - s)^p-

1

≤ max [-_π Γ(p)

Γ(p)

∫^t(t

0

1

- ∣ρ(a, β, ω, s, L∞, v(s))∣ds]

_-

_-

s)? ¹ ∣ρ(a,β,ω,s,L∞,v(s))

ρ(a,β, ω,s,L∞,0) + ρ(a,β,ω,s,L∞,0)∣ds]

(Πv)(t)

1 C^t

≤T(p)j (^t - s) ∣ρ(a,β,ω,s,L∞,v(t))∣ds∣

≤⅛∙t---

B∣∣v∣∣t^p     _{l    l}

⅛⅛≤ l∣v∣l

Γ(p + 1)    ^{1   1}

≤ FT> J (t-s)^{p 1} ∣ρ(a,β,ω,s,L∞,v(s)) ^γ(p).∕o                I

- ρ(a,β,ω,s,L∞,0)∣ds

1

⁺ γ(P)

∫ (t-s)^{p 1} ∣ρ(a,β,ω,s,L∞,0)∣ds]

Lrt^p      Mt^p     t^p(Lr + M)

<--1--< —------- < r

≤ Γ(p + 1) Γ(p + 1) ≤ Γ(p + 1)  ≤

Thus we have ∣∣∏v(t)∣∣ ≤ ∣∣v∣∣, v ∈ ∂B, Since the operator Π has at least one fixed point according to theorem (3.1), it follows that the problem (5) has at least one solution.

For v,y ∈ (C[0,1],R) and for t ∈ [0, T], we obtain:

∣∣(Πv)(t) - (Πy)(t)∣∣

Theorem 4.2. Assume that

ρ(a,β,ω,t,L∞,v(t)): [0,∞] × [0,∞] × [0,∞] × [0, T] × [0, ∞] × R → R

is jointly continuous function satisfying the following condition:

∣∣ρ(a,β,ω, t,L∞,v(t)) -

ρ(a, β, ω, t, L∞, y(t))∣ ∣ ≤L∣∣v-y∣∣,

∀ t ∈ [0,T],a ∈ [0,∞],β ∈ [0,∞],ω

∈ [0,∞],L∞ ∈ [0,∞],v,y

∈ R

≤ max

Γ ^t(t - s)^{p-1 1} o^(PΓ

∣ρ(a,β,ω,s,L∞,v(s))

- ρ(a,β,ω, s,L∞,y(s))∣ds

_< L∣^|v -y^||t^p

^- Γ(p + 1)

≤ B∣∣v-y∣∣

With

Where

Lt^p B =------

Γ(p + 1)

As B < 1, Π is contraction. Thus, the contraction mapping principle leads to the theorem's conclusion.

0.5Γ(p + 1) ≤     t?

then problem (5) has a unique solution.

Proof. Setting

sup             ρ(a,β,ω,t,L∞,0)

'∙ ∙,∙ ^

t∈[0,T],a∈[0,∞],∕3∈[0,∞],ω∈[0,∞],L∞∈[0,∞]

= M

and selecting

5. CONCLUSION

This article's goal is to examine the dynamics of the deterministic, stochastic, and fractional Von Bertalanffy model in order to ascertain how changing parameter values impact population behavior. The impacts of various beginning conditions and K are taken into consideration. After an initial transient, the model continues to behave in the same way throughout time. This indicates that if the length

growth rate of organisms rises, the length (or any other size-measure) of the organism will reach the asymptotic length more quickly, which will cause the population to cease increasing early.

We demonstrated the existence of the solution and its uniqueness using the Banach's fixed point theorem after solving the fractional Von Bertalanffy differential equation with periodic modulation.

The Von Bertalanffy deterministic model has been extended to stochastic setting by perturbing the growth rate parameter K to include (a + β cos ω t).

It will be interesting to investigate different models using similar methods in the future.

REFERENCES

Vaidya, Vinay G., and Frank J. Alexandro Jr. "Evaluation of some mathematical models for tumor growth." International journal of bio-medical computing 13, no. 1 (1982): 19-35.

M. H. Zwietering, I. Jongenburger, F. M.

rombouts and K. Van't riet, ‘’Modeling of the bacterial growth curve’’, App. and Enviro. Microbiology, (56) (1990), 18751881.

P.  Waliszewski, and J. Konarski, ‘’The

Gompertzian curve reveals fractal properties of tumor growth), Chaos, Solitons and Fractals (16) (2003), 665-674.

A. K. Laird, ‘’Dynamics of tumour growth’’, Br. J. Cancer, (18) (1964), 490.

A. K. Laird, ‘’Dynamics of tumour growth: comparison of growth rates and extrapolation of growth curve to one cell’’, Br. J. Cancer, (19) (1965), 278-291.

Tabassum, Shabana, Norhayati Binti Rosli, and Mazma Sayahidatul Ayuni Binti Mazalan. "Mathematical modeling of cancer growth process: a review." In Journal of Physics: Conference Series, vol. 1366, no. 1, p. 012018. IOP Publishing, 2019.

Lee, Laura, David Atkinson, Andrew G. Hirst, and Stephen J. Cornell. "A new framework for growth curve fitting based on the von Bertalanffy Growth Function." Scientific reports 10, no. 1 (2020): 7953.

Garcia, Oscar. "A stochastic differential equation model for the height growth of forest stands." Biometrics (1983): 1059-1072.

E. Konig, Cabezas, H. and A. L. Mayer, ‘’Detecting dynamic system regime boundaries with Fisher information: the case of ecosystems’’, Clean Techn Environ Policy, (21) (2019).

A. AL-Saffar and E. Kim, ‘’Sustainable theory of a logistic model-Fisher information approach’’, Math. Biosciences, (285) (2017), 81-91.

Al-Saffar, Avan, and Eun-jin Kim. "Fisher information approach to understand the Gompertz model." Mathematics in Applied Sciences and Engineering (2020): 1-11.

Y. Wang, S. Liu, H. Li, D. Wang, ‘’On the spatial Julia set generated by fractional Lotka-Volterra system with noise’’, Chaos, Solitons & Fractals, 128(2009), 129-138.

E. Ahmed, A. S. Elgazzar, On fractional order differential equations model for nonlocal epidemics, Physica A: Statistical Mechanics and its Applications 379(2007), 607-614.

A. Kilicman, A fractional order SIR epidemic model for dengue transmission, Chaos, Solitons \& Fractals 114 (2018), 55-62.

Ahmad, B. and Ntouyas, S., A four-point nonlocal integral boundary value problem for fractional differential equations of arbitrary order, Electronic Journal of Qualitative Theory of Differential Equations, (22), pp. 1-15, 2011.

Ishak, Faraj Y. "Mixed Boundary Value Problem for Nonlinear Fractional Volterra Integral Equation." Jurnal Matematika MANTIK 8, no. 2 (2022): 89-98.

Ishak, Faraj Y. "Existence and uniqueness solution for fractional volterra equation with fractional anti-periodic boundary conditions.’’ Palestine Journal of Mathematics 12, no. 1 (2023).

Agarwal, Ravi P., and Bashir Ahmad. "Existence theory for anti-periodic boundary value problems of fractional differential equations and inclusions." Computers & Mathematics with Applications 62, no. 3 (2011): 12001214.

Ishak, F. Y., Existence Solution for Nonlinear System of Fractional Integrodifferential Equations of Volterra Type with Fractional Boundary Conditions, Jurnal Matematika MANTIK, 6(1), pp. 1-12, 2020.

Ishak, F. Y., Existence, uniqueness and stability solutions for new nonlinear system of integro-differential equations of Volterra type, E-Jurnal Matematika, 9(2), pp.109116, 2020.

199

2