A Practical Analysis of the Fermat Factorization and Pollard Rho Method for Factoring Integers
on
LONTAR KOMPUTER VOL. 12, NO. 1 APRIL 2021
DOI : 10.24843/LKJITI.2021.v12.i01.p04
Accredited Sinta 2 by RISTEKDIKTI Decree No. 30/E/KPT/2018
p-ISSN 2088-1541
e-ISSN 2541-5832
A Practical Analysis of the Fermat Factorization and Pollard Rho Method for Factoring Integers
Aminudina1, Eko Budi Cahyonoa2
aDepartment of Informatic, University of Muhammadiyah Malang Tlogomas Street 246 Malang, Indonesia 1aminudin2008@umm.ac.id (corresponding author) 2ekobudi@umm.ac.id
Abstract
The development of public-key cryptography generation using the factoring method is very important in practical cryptography applications. In cryptographic applications, the urgency of factoring is very risky because factoring can crack public and private keys, even though the strength in cryptographic algorithms is determined mainly by the key strength generated by the algorithm. However, solving the composite number to find the prime factors is still very rarely done. Therefore, this study will compare the Fermat factorization algorithm and Pollard rho by finding the key generator public key algorithm's prime factor value. Based on the series of test and analysis factoring integer algorithm using Fermat's Factorization and Pollards' Rho methods, it could be concluded that both methods could be used to factorize the public key which specifically aimed to identify the prime factors. During the public key factorizing process within 16 bytes – 64 bytes, Pollards' Rho's average duration was significantly faster than Fermat's Factorization.
Keywords: Factorization, Fermat's Factorization, Pollard's Rho.
Information security is a major challenge in an era of information flood like today. The cryptology method can be one of the solutions used to secure this information [1]. Cryptology consists of two parts, namely cryptography and cryptanalysis. The main task of cryptography is to hide data using specific algorithms, while cryptanalyst is a method for investigating the security of a cryptographic system by finding weaknesses in codes, ciphers, protocols, or key management schemes.[2]. Usually, cryptanalysis refers to analyzing and solving the keys used to perform the encryption and decryption processes. Therefore, cryptanalysts are needed to test the robustness of the encryption algorithm. There are several mathematical approaches in testing the robustness of cryptographic algorithms, including discrete logarithms and factorization. In this study, the factorization method is used to break numbers into smaller numbers [3]. This factorization method is used for the RSA algorithm to generate public and private keys
There are several methods that can be used to factor the composite number into prime numbers, namely Fermat's factorization and Pollard rho. Fermat factorization looks for the factor of an odd number by utilizing the property of an odd number which can be expressed as the difference of 2 squares from another number [4]. In contrast, the pollard rho method integrates a polynomial function in a modulo n (the number to be factored) and a seed (generator number) [5]. The importance of the two algorithms is that if they can return two large prime factors of modulus processing, it can be ascertained that the public and private keys can be found [6]. Thus, this integer factorization problem has a significant impact on the security of the public-key cryptography system. The research conducted by Chinniah et al. created a factorization method that aims to find composite number factors resulting from two different prime numbers [7]. Then Li et al. researched the implementation of algorithms with a mathematical model used for factoring integers. The results of this study were a comparison between Pollard's Rho and SpSqAlgorithm based on execution time. [8]. This study aimed to analyze Fermat's Factorization and Pollards' Rho due to vulnerability by factorizing the prime factors. Furthermore, the purpose is to figure out the receiving the factorization attack by comparing the factorization time between both methods.
The ultimate goal of the proposed research is to discover an opportunity to extend the previous study to contribute in the area of cryptanalysis and cryptography.
The following section is the attack method as the technique of factorization. p and q can be easily found using Fermat's Factorization with the following steps [6]:
The variable of k on equation (1) is the value of square root n. The variable of k2 on equation (2) is the value of the perfect square. The variable of h2 on equation (4) is the ultimate value of the perfect square. The variable of p and q on equation (5) is the sought prime. Figure 1 shows the pseudocode of Fermat's factorization.
Input : value public key (n)
Output: p and q
for k from ceil (sqrt (n)) to n h square = k * k-n
if p > 1 and p < n do
h = sqrt (hSquared)
p = k + h
q = k – h
Figure 1. Flowchart Fermat's Factorization Algorithm
The input value of n is used to get factorization from values p and q. The n value will be checked to include square root or not. After knowing k is the square root, it is processed again whether q is greater than n. Subsequently, the calculations can be done if the value k is greater than the value n. If it has a greater value, it proceeds by calculating the result of k by performing square root.
Conversely, the calculation is continued by adding 1 to the value k. After obtaining the square root value of n, we find p and q values depicted in equation (8) to get the p and q values. The flowchart of Fermat's Factorization is shown in Figure 2.
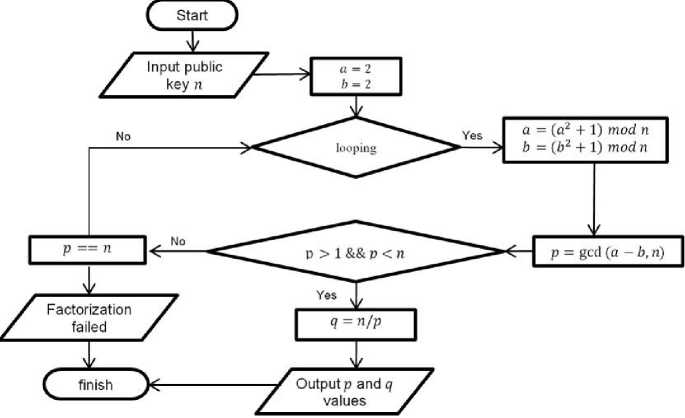
Figure 2. Flowchart of Fermat's Factorization Algorithm
Figure 5 represents the factorization steps using Fermat's factorization method that have already been explained through a flow chart.
Pollard's Rho factorization method calculates the factorization n with polynomial modulo n iteration. This algorithm is based on several mathematical concepts, such as integer factorization[9]. The following procedure explains the steps of Pollard's Rho algorithm as a method of factorization [2]:
-
a. Input a value that are going to be factorized value n
-
b. a = 2,b = 2. (5) c. a = a2 + 1 (mod n),b = b2 + 1 (mod n) (6) d. p = gcd(a — b,n). (7) e. p ≠ 1 and p ≠ n. (8) f. 1 <p <n, q = n/p (9)
The a and b variable on equation (5) is the first step of factorization. The a2 and b2 variable on equation (6) is the value that has been square root from the previous result. The p variable on equation (7) is the prime produced by equation gcd (the greatest divisor), and the n variable is the prime of the public key. The q variable on equation (8) is the prime generated from the division of variable n and variable q. Figure 3 shows pseudocode pollard's Rho in detail.
Input : value public key (n) Output: p and q values initialization a=2,b=2;
while (true) a=(a2 + 1(mod n))
b=(b2 + 1(mod n))
count p = (a - b), gcd (n); print (p);
loop (a,b);
if p > 1 and p < n than
count q = (n/p);
print (q);
Figure 3. Pollard's Rho Algorithm
The first step in the pollards' rho method gets the public key value n to be factored into p and q values. The next step is calculating the p value, which must fulfill the equation p > 1 dan p <n. If it does not fulfill the equation, it is recalculated from the beginning. If the p value has been found, then the q value can be calculated.
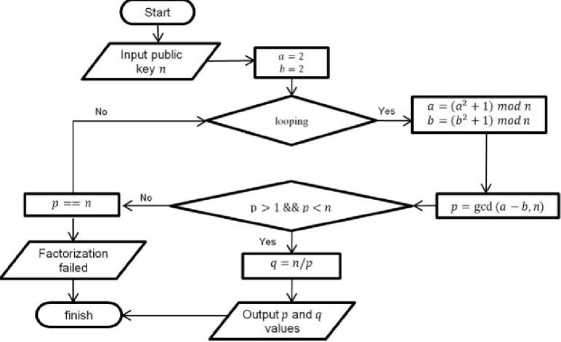
Figure 4. Flowchart of Pollard's Rho
Figure 7 represents the factorization steps using Pollard's Rho method that have already been explained through a flow chart.
The testing scenario was conducted by running the program and inserting the various number of public keys that have been generated and compiled using n = p < q <2p which finally created the public key n. Then the generated key was factorized by using Fermat's Factorization and Pollard's Rho method for obtaining the p and q values and figuring out the duration of factorization. The public key pairs were created within a range from 16 to 64 bytes complying with the equation n = p < q <2p.
To increase the security in public key so that it can be concluded afterward the characteristic of the strong public key that can withstand the attacks of factorization mainly by using the Fermat's Factorization and Pollard's Rho. The test results of Fermat's factorization method are presented in Table 1 and Table 2, while Pollard's Rho's test results are shown in Tables 3 and 4. The second column shows the public key n factorized to obtain the value of p and q. The following columns present the digit length of n, the found value of p and q, duration of factorization, and success rate of key public factorization.
The experiment of Fermat's Factorization algorithm used the public key n that was normally widely distributed. However, this test used the generated public key n with the equation n = p < q <2p to make it difficult to find the value of p and q. Fermat's factorization was used to factorize the public key n to find the value of p and q. The test results are illustrated in Table 1 and Table 2 below:
Table 1. Testing Result Fermat's Factorization on 16 Untuk 32 Bytes Key Generation
|
No |
Public Key n |
Length of Public Key n |
P |
q |
Execution Time (ms) |
Succes s Rate (%) |
|
1. |
2916425411 |
10 /16 bytes 14 |
65357 |
44623 |
561 ms |
100 % |
|
2. |
1175270081425 9 |
343051 7 |
3425927 |
2 ms |
100 % | |
|
3. |
1341849068550 433 |
16 |
393584 47 |
3409303 9 |
18497 ms / 18,497 d |
100 % |
|
4. |
4172366223726 |
17 |
209763 |
1989077 |
13207 ms / |
100 % |
|
2923 |
919 |
17 |
13,207 d | |||
|
5. |
4325011719545 |
18 |
779594 |
5547769 |
1640872 ms / |
100 % |
|
94013 |
677 |
69 |
27,34786667 m | |||
|
6. |
8763301721976 902561 |
19 |
344668 3453 |
2542531 637 |
6688088 ms /1,857802222 jam 6162 ms / 6,162 |
100 % |
|
7. |
4980853165476 |
20/ 32 |
707853 |
7036556 |
100 % | |
|
5413631 |
bytes |
7649 |
719 |
d |
In Table 1, Fermat's Factorization method succeeded in finding the value of p and q. This showed the attack's susceptibility caused by Fermat's Factorization method, proven by a 100% success rate. The prime factors of public key n were still easily obtained through the test. The test used Fermat's Factorization within 32-64 bytes key generation.
|
Table |
2. Testing Result Fermat's Factorization on 32 Untuk 64 Bytes Key Generation | ||||
|
N o. |
Public Key n |
Length of Public Key of n |
p q |
Execution Time (ms) |
Succes s Rate (%) |
|
1. |
2936653455160738453027 |
22 |
- - |
469 m 4 s / 7,81667 h |
0 % |
|
2. |
52891073208710727120157 |
23 |
- - |
383 m 34 s / 6,38333 h |
0 % |
|
3. |
147307994954025982922977 1 |
25 |
- - |
385 m 40 s / 6,41667 h |
0 % |
|
4. |
123693524037686594532150 77 |
26 |
- - |
517 m / 8,61667 h |
0 % |
|
5. |
268889892902937863375973 328747 |
30 |
- - |
540 m 5 s / 9 h |
0 % |
|
6. |
568396900241882051501949 76305169 |
32 |
- - |
967 m 38 s / 16,1167 h |
0 % |
|
7. |
205777995053692340932379 163614957396549 |
38/ 64 bytes |
- - |
30357 s / 5,05 h |
0% |
In Table 2, Fermat's factorization method did not find the value of p and q. This was considered secure from Fermat's Factorization attack, proven by a 0% success rate in which the prime factors of public key n were not found.
Fermat's factorization is used to identify the factors of public key n (the value of p and q) by factorizing the value of the public key. The test of Fermat's Factorization algorithm showed a 100% success rate in finding the value of p and q at 16 - 32 bytes key generation, even though the key public generation has fulfilled the equation n = p < q < 2p used to complicate the identification of the prime factors through Fermat's Factorization. Meanwhile, the key generation on variant above 32 – 64 bytes showed a 0% success rate.
The second test applied Pollards' Rho method to factorize the public key n to identify the prime factors' values on variant above 32 – 64 bytes. The duration of factorization was also investigated. The test results are presented in Table 3 and Table 4 below :
|
Table 3. Testing Result Pollard's Rho on 16 Until 32 Bytes Key Generation | ||||||
|
No |
Public Key n |
Length of Public Key n |
p |
q |
Executio n Time (ms) |
Success Rate (%) |
|
1. |
2916425411 |
10/16 bytes |
44623 |
65357 |
8892 ms / 8,892 d |
100 % |
|
2. |
1175270081425 9 |
14 |
3425927 |
3430517 |
7394 ms / 7,394 d |
100 % |
|
3. |
1341849068550 |
16 |
3935844 |
3409303 |
9843 ms / |
100 % |
|
433 |
7 |
9 |
9,843 d | |||
|
4. |
4172366223726 |
17 |
1989077 |
2097639 |
8564 ms / |
100 % |
|
2923 |
17 |
19 |
8,564 d | |||
|
5. |
4325011719545 94013 |
18 |
5547769 69 |
7795946 77 |
5148 ms / 5,148 d |
100 % |
|
6. |
8763301721976 |
19 |
2542531 |
3446683 |
8440 ms / |
100 % |
|
902561 |
637 |
453 |
8,44 d | |||
|
7. |
4980853165476 |
20/ 32 |
7078537 |
7036556 |
28704 ms |
100 % |
|
5413631 |
bytes |
649 |
719 |
/ 28,704 | ||
In Table 3, the Pollards' Rho method succeeded in solving the public key n so that the prime factors (p and n) were still identifiable. This proved by the 100% of prime factors from the
established public key n using a variant of 16 - 32 bytes. This happened since the method easily factorized the key. If a prime n is the product of two contiguous numbers (p, q), then n = p.q with p ≥p > 0,p q is not really big, and both of p and q) are even, then p and q are easily identified by Pollard's Rho method and eventually accelerate the factorization process.
Table 4. Testing Result Pollard's Rho on 32 Until 64 Bytes Key Generation
|
No. |
Public Key n |
Public Key |
V |
(I |
Execution Time (ms) |
Success Rate (%) |
|
1. |
29366534551607384530 27 |
22 |
49865 64726 7 |
58891313 281 |
27737 ms / 27,737 d |
100% |
|
2. |
14730799495402598292 |
25 |
11043 88782 |
13338418 |
108280 ms / |
100% |
|
29771 |
851 |
24921 |
1,80466667 m | |||
|
3. |
12369352403768659453 |
26 |
34822 18272 |
35521473 |
224082 ms / |
100% |
|
215077 |
409 |
48653 |
3,7347 m | |||
|
4. |
26888989290293786337 |
30 |
53122 50579 49433 |
50616944 |
6003859 ms / |
100% |
|
5973328747 |
5283459 |
1,667738611 h | ||||
|
5. |
56839690024188205150 |
32 |
80319 78041 |
70766739 |
24835270 ms / 6,8986861111 h |
100% |
|
194976305169 |
99680 9 - |
80804041 | ||||
|
6. |
20577799505369234093 2379163614957396549 |
38 |
- |
1,194 m 34 s / 19,9 h |
0% |
In Table 4, the Pollards' Rho method was still able to solve the factors of public key n on variants below 64 bytes. Meanwhile, the method could not identify the factors of key public n on variant at above 64 bytes. It was proved by the 0% success rate indicating that the value of p and q of the public key prime factors were not found. These test results proved that the success of public key generation fulfilling the equation n = p < q < 2p used above 64 bytes variant was still secured.
The analysis on the comparison of public key n factorization duration during the attack using Fermat's Factorization and Pollard's Rho showed varieties of durations and key length. The two methods with the fastest rate in the factorizing public key under 64 bytes can be depicted from the results. The duration comparison using 16 – 64 bytes prime length parameter on each test is presented in Figure 8. Figure 8 shows that along with the public key's growth, the factorization process from both methods spending more time and resources. The highest point for the length of public-key n in Fermat's Factorization reached 32 digits, while the highest point in Pollards' Rho reached 38 digits. In terms of the factorizing the public key n within 16 – 64 bytes, Pollard's Rho generated faster duration (7129203,29 milliseconds or 118,82005483332 minutes or 1,980334247222 hours) than Fermat's Factorization (15871956,36 milliseconds or 264,532606 minutes or 4,4088767666667 hours. More information can be obtained if a higher specification is provided.
Comparison of Algorithm Duration
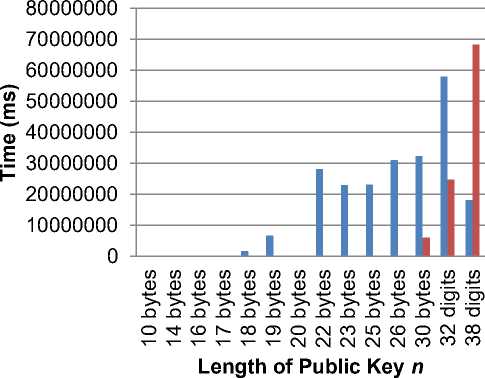
■ Fermat's Factorization
■ Pollards' Rho
-
Figure 8. Comparison Duration on the Factorization
Based on the series of test and analysis factoring integer algorithm using Fermat's Factorization and Pollards' Rho methods, it could be concluded that both methods could be used to factorize the public key which specifically aimed to identify the prime factors (p and q). During the public key n factorizing process within 16 bytes – 64 bytes, Pollards' Rho's average duration was significantly faster than Fermat's Factorization. Pollard's Rho performed factorization only in 7129203,29 milliseconds or 118,82005483332 minutes or 1,980334247222 hours, while Fermat's Factorization was accomplished in 15871956,36 milliseconds or 264,532606 minutes or 4 hours.
References
-
[1] A. Aminudin, A. F. Helmi, and S. Arifianto, “Analisa Kombinasi Algoritma Merkle-Hellman Knapscak dan Logaritma Diskrit pada Aplikasi Chat,” Jurnal Teknologi Informasi dan Ilmu Komputer, vol. 5, no. 3, pp. 325–334, 2018.
-
[2] P. P. Thwe, M. Htet, Y. C. City, and I. Technology, "Extended Pollard's Rho Factorization Algorithm For Finding Factors In Composite Number," Journal of Science, Engineering and Education, pp. 232–235, 2020. doi: 10.13140/RG.2.2.34889.16485
-
[3] A. Aminudin, G. P. Aditya, and S. Arifianto, "RSA algorithm using key generator ESRKGS to encrypt chat messages with TCP/IP protocol," Jurnal Teknologi dan Sistem Komputer, vol. 8, no. 2, pp. 113–120, 2020, doi: 10.14710/jtsiskom.8.2.2020.113-120.
-
[4] K. Chiewchanchairat, P. Bumroongsri, and S. Kheawhom, "Improving Fermat factorization algorithm by dividing modulus into three forms," KKU Engineering Journal, vol. 40, no. March, pp. 131–138, 2016, doi: 10.14456/kkuenj.2016.127.
-
[5] C. L. Duta, L. Gheorghe, and N. Tapus, "Framework for evaluation and comparison of integer factorization algorithms," Proceeding 2016 SAI Computing Conference, pp. 1047–1053, 2016, doi: 10.1109/SAI.2016.7556107.
-
[6] K. Somsuk, "The new integer factorization algorithm based on Fermat's Factorization Algorithm and Euler's theorem," International Journal of Electrical and Computer Engineering, vol. 10, no. 2, pp. 1469–1476, 2020, doi: 10.11591/ijece.v10i2.pp1469-1476.
-
[7] P. Chinniah and A. Ramalingam, "An Integer Factorization Method Equivalent to Fermat Factorization," International Journal of Mathematics And its Applications, vol. 6, no. 2, pp. 107–111, 2018.
-
[8] J. LI, "Algorithm Design and Implementation for a Mathematical Model of Factoring Integers," IOSR Journal of Mathematics, vol. 13, no. 01, pp. 37–41, 2017, doi: 10.9790/5728-
1301063741.
-
[9] S. Sarnaik, R. Bhakkad, and C. Desai, "Comparative study on Integer Factorization algorithm-Pollard's RHO and Pollard's P-1," in 2015 2nd International Conference on Computing for Sustainable Global Development (INDIACom), 2015, pp. 677–679.
40
Discussion and feedback