PENGGUNAAN ALGORITMA GORTZEL UNTUK DETEKSI FREKUENSI DTMF BERBASIS PROCESSOR DSP TMS320C31
on
Penggunaan Algoritma Gortzel …
Putra Sastra
PENGGUNAAN ALGORITMA GORTZEL UNTUK DETEKSI FREKUENSI DTMF BERBASIS PROCESSOR DSP TMS320C31
Nyoman Putra Sastra
Staf Pengajar Program Studi Teknik Elektro – Universitas Udayana
Intisari
Algoritma Gortzel yang diturunkan dari DFT (Discrete Fourier Transform), dapat digunakan untuk mendeteksi frekuensi dengan bantuan processor DSP TMS320C31. Algoritma Gortzel mendeteksi frekuensi dengan tingkat keberhasilan pendeteksian sangat tergantung pada jumlah cuplikan (N), semakin banyak jumlah cuplikan maka semakin akurat pendeteksian frekuensi tersebut. Akan tetapi semakin banyak jumlah N, maka proses iterasinya menjadi lebih kompleks, sehingga waktu yang diperlukan untuk melakukan pendeteksian semakin lama. Untuk itu perlu dipilih jumlah N yang digunakan agar waktu yang diperlukan sesingkat mungkin.
Kata Kunci: Algoritma Gortzel, DSP, Frekuensi DTMF
Pengolahan Sinyal digital atau digital signal processing (DSP) adalah suatu sistem pengolahan sinyal menggunakan teknologi solid state yang mulai populer pada tahun 1960. Perkembangan DSP selanjutnya adalah mulai digunakannya teknologi medium scale integrated (MSI) dan large scale integrated (LSI) circuit sebagai bagian dari programmable signal processors yang diimplementasikan untuk aplikasi realtime signal processing.
Perkembangan DSP terus berlanjut dengan digunakannya teknologi very large scale integrated (VLSI) circuit dan very high speed integrated circuit (VHSIC) yang menyediakan berbagai kemampuan untuk membangun arsitektur distributed signal processor.
DSP dewasa ini banyak digunakan untuk aplikasi pemrosesan sinyal secara real-time, yaitu pengolahan sinyal input untuk menghasilkan sinyal output dengan delay minimum. Contoh dari penggunaan aplikasi realtime yaitu untuk keperluan navigasi, radar dan komunikasi.
Transformasi Fourier adalah suatu transformasi yang mengubah suatu sinyal dari domain waktu ke domain frekuensi. Suatu sinyal dalam domain waktu dapat diubah menjadi sinyal dalam domain frekuensi dengan menggunakan persamaan dasar:
'
X (ω )= ∫ X (t) e - 'wtdt (1)
-∞
dengan suatu metode dimana mesin dapat melakukan komputasi tersebut. Pendekatan yang digunakan adalah dengan menggunakan suatu Transformasi Fourier Diskrit
∞
X (ω )= ∑ X (n). e - w (2)
n =-∞
Frekuensi X(ω) dicuplik (sampling) secara periodik dengan jarak dω . radian antara cuplikannya. Karena X(ω) berulang secara periodik dengan periode 2π maka yang diperlukan hanya cuplikan yang terdapat pada frekuensi dasar. Misalkan kita gunakan N cuplikan pada interval 0 ≤ ω < 2π dengan jarak dω =2n/N maka N adalah jumlah sample dalam domain frekuensi, dan sesuai dengan persamaan 2 pada ω= 2nk/N kita dapatkan:
Xt~k × X(n).e ■ /N k=0,1,2--., N-I (3)
j TV } ’
V1' ∕ n=-∞
Pada akhirnya deret x(n) dalam durasi finit dengan panjang L, contoh x(n)=0, .untuk n < 0 dan n ≥ L mempunyai transformasi Fourier sebagai berikut.
X(k) ≡ X(—k 1 = LTx(n).eπ/N
IN J n=0
L-Iftuntuk k=0,1,2^,N-1 (4)
X(k) =∑ χ (n WN
dimana WN = e-'2π / N
Untuk menghitung suatu transformasi Fourier dengan perangkat keras digital, persamaan 1 harus didekati
3. ALGORITMA GORTZEL
Algoritma Gortzel diturunkan dari transformasi Fourier Diskrit (DFT) sebagai berikut :
£ kn k=0,1,2,..., N-1 (5)
X(k) = ∑ x(n Wn
n=0
Selain digunakan menghitung DFT secara langsung, Algoritma Gortzel juga digunakan sebagai filter infinite impulse response (IIR). Penghitungan dilakukan secara rekursif. Bila informasi magnitude saja yang diperlukan, perkalian kompleks dapat dihindari. Sebuah filter dapat diturunkan dari DFT sebagai berikut:
yk(n) = wk(n)-exp(-j2^k/n).wk(n-1) (13)
Dengan kondisi inisialisasi wk(-1)=wk(-2)=0.
Persamaan rekursifnya diiterasi untuk n = 0,1,…,N, tetapi untuk persamaan berikutnya hanya dihitung satu kali saja yaitu pada n=N. Tiap iterasi memerlukan satu buah perkalian real dan dua buah penjumlahan. Konsekuensinya untuk deret input real x(n), algoritma ini memerlukan N+1 perkalian jadi bukan saja X(k) tetapi juga nilai dari X(N-k).
Kedua persamaan ini dapat digambarkan sebagai berikut.
y(n) = x(n)*h(n)
N-1
∑ x(m^h(n - m)
m=0
N-1
∑ x (m)-e
m=0
(—j 2 πk (nm)) / N
(6)
dimana filter :
- j 2πkn
h(n) = e n u (n) (7)
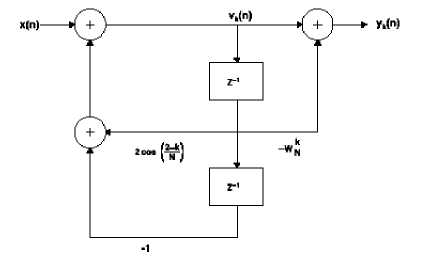
Gambar 1 Filter Gortzel untuk menghitung DFT
jika ditransformasi-Z-kan diperoleh:
H (z) =
1
- j 2 πk
(8)
1 - e n . Z
untuk menghindari perkalian kompleks maka filter di atas dikalikan konjugat kompleks polenya, sehingga dihasilkan persamaan sebagai berikut:
Hk (z) =
ι - wN. z -1_________
1 - 2cos(2π.k/N).z 1 + z ξ
(9)
Filter ini akan mengevaluasi DFT pada frekuensi yang sesuai dengan anggota deret k.
Untuk implementasi pada filter IIR, maka:
W(z) X(z)
akan diperoleh persamaan perbedaan sebagai berikut.
wk(n) = 2 cos (2^k/N).
dan
-
4. TMS320C3X DSP STARTER KIT (DSK)
DSP Starter Kit (DSK) dibuat dengan biaya rendah (low-cost) dan bentuknya sederhana (simple) tetapi unjuk kerja yang tinggi, misalnya untuk membuat program aplikasi dengan menggunakan TMS320C3x DSP real-time processing.
DSK mempunyai prosesor TMS320C31 pada boardnya dan berkecepatan tinggi (full-speed) dalam pengujian kode TMS320C3x. DSK juga memberi kebebasan untuk membuat board tambahan, membuat perangkat lunak sendiri pada host PC, download perangkat lunak ke DSK dan menjalankan perangkat lunak pada DSK board. DSK juga menyediakan debugger dengan windows-oriented. Adapun spesifikasi DSK ini adalah sebagai berikut.
-
□ Menggunakan TMS320C31 floating point Digital Signal Processing yang telah distandardisasi untuk industri.
-
□ Dapat melakukan satu buah intruksi dalam 40 ns, 50 MFLOPS, 25 MIPS. Sehingga dapat dikembangkan untuk mengolah sinyal lebih dari satu kanal.
Menggunakan antarmuka paralel port printer yang dapat dihubungkan dengan host PC dan TMS320C31 ini dapat berkomunikasi dengan program yang dibuat pada PC dengan menggunakan bahasa Assembler dan bahasa
-
□ Dapat digunakan untuk mengolah sinyal digital dan analog. Sinyal analog diolah melalui rangkaian antarmuka analog yang menggunakan TLC32040. Rate analog to digital converter (DAC) dapat diubah-ubah dengan range dinamik 14-bit pada 20.000 samples/s. Mempunyai filter rekonstruksi output dan menggunakanan switched-capasitor anti aliasing pada input filternya.
-
□ Untuk pengolahan sinyal yang memerlukan intsruksi panjang maka DSK dapat diekspansi dengan cara menambahkan daugtherboards berisi RAM atau ROM.
-
□ Standar RCA plug connector untuk input/output analog dapat dihubungkan langsung ke mikrofon dan speaker.
-
□ Mempunyai XDS510 emulator connector
-
□ Mempunyai Expansion connector.
Selain menggunakan filter analog, deteksi frekuensi secara real time dapat menggunakan Processor DSP yang menggunakan algoritma tertentu. Dalam penelitian processor DSP akan digunakan untuk mendeteksi DTMF (Dual Tone Multifrekuensi) pada R2 Signalling. Algoritma yang digunakan adalah Algoritma Gortzel.
Frekuensi cuplikan yang digunakan adalah 8 kHz. Harga ini dipilih karena pencuplikan yang dilakukan oleh PCM adalah 8 kHz, sehingga bila prototipe ini dikembangkan untuk mengakses kanal digital perangkat lunak ini lebih mudah diimplementasikan. Langkah pertama adalah mencari harga N sehingga didapatkan harga k yang sesuai Diperoleh harga k untuk masing-masing frekuensi yang berturutan minimal berbeda satu angka. Untuk percobaan I, orde filter yang digunakan N = 91, untuk harga k, dapat dilihat pada 1 sebagai berikut.
Sebelum algoritma pendeteksian dimulai, input sinyal dicuplik 91 kali dan disimpan dalam memori yang berisi 91 tempat memori. Harga koefisien, cos (2^k/N) dan sin(2^k/N), di-pre-store dalam lokasi memori yang mempunyai 16 tempat memori. Sehingga ada dua buah operasi pemanggilan penambahan pada bagian rekursif dari fungsi filter di atas. Diperlukan dua buah memori yang mengakses untuk melakukan pemanggilan ini.
Satu set koefisen, sinus dan cosinus, digunakan untuk menghitung sebuah frekuensi DTMF R2. Program ini selalu melakukan pergeseran memori pada saat menghitung harga v1 yang baru. Variabel keadaan, v1 dan v2, diinisialisasi dengan harga nol. Ketika harga v1 yang baru dihitung, v1 yang lama akan digeser ke lokasi memori v2. Karena ini merupakan operasi rekursif maka masing-masing variabel keadaan bergantung pada harga sebelumnya. Dengan kata lain
tidak boleh ada instruksi yang dihilangkan atau diabaikan. Operasi rekursif ini diulang sesuai dengan jumlah sample, 91 kali (N). Operasi rekursif terakhir digabung dengan bagian non-rekursifnya.
Tabel 1 Harga k untuk N = 91
|
Frekuensi (Hz) |
k |
|
540 |
6 |
|
660 |
8 |
|
780 |
9 |
|
900 |
10 |
|
1020 |
12 |
|
1140 |
13 |
|
1380 |
16 |
|
1500 |
17 |
|
1620 |
18 |
|
1740 |
20 |
|
1860 |
21 |
|
1980 |
23 |
Penghitungan energi menggunakan persamaan 13. X(k) dikalkulasikan terpisah antara bagian real dan imajinernya. Energi didapat dengan cara menjumlahkan kuadrat dari bagian real dan imajinernya (disebut dengan |X(k)|2). Energi dari frekuensi DTMF R2 yang pertama dibandingkan dengan energi maksimum yang telah diinisialisasi dengan harga nol dan disimpan pada alamat memori. Energi yang lebih besar disimpan kembali pada alamat memori dengan indeksnya yang mengindikasikan frekuensi yang mempunyai energi yang lebih besar.
Kemudian variabel keadaan diinisialisasi lagi dengan harga nol, pointer direset ke sinyal input awal, dan penghitungan kedua dimulai lagi. Penghitungan ini diulang terus sampai energi yang terakhir dihitung. Ketika proses pembandingan ini berakhir maka diperoleh dua buah energi yang tertinggi dan indeksnya.
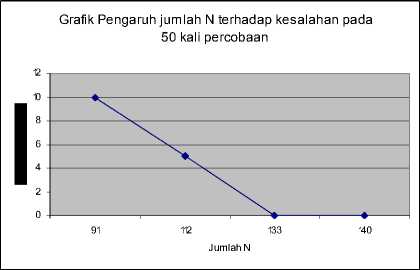
Pada percobaan dengan cuplikan (N) = 91 kali menghasilkan data energi pada 12 alamat memori yang mempunyai perbedaan nilai yang tidak terlalu besar. Kadang juga terjadi kesalahan pendeteksian akibat nilai energi dari frekuensi yang dikirim ternyata mempunyai nilai yang lebih kecil dari energi frekuensi yang tidak dikirim. Maka hasil dengan N=91 ini dapat dikatakan tidak akurat.
Karena hasil yang tidak akurat tersebut maka dilakukan beberapa kali percobaan dengan mengubah-ubah nilai N. Pendesainan ulang nilai N dilakukan sebanyak tiga kali, yaitu menggunakan N=112, N= 133,
dan N = 140. Hasil percobaan ini dapat dilihat pada tabel 2 sebagai berikut.
Tabel 2 Harga k untuk N = 112, 133 dan 140
|
Frekuensi (Hz) |
k | ||
|
N=112 |
N=133 |
N=140 | |
|
540 |
7 |
9 |
10 |
|
660 |
8 |
11 |
12 |
|
780 |
10 |
13 |
14 |
|
900 |
11 |
15 |
17 |
|
1020 |
13 |
17 |
19 |
|
1140 |
15 |
19 |
21 |
|
1380 |
17 |
23 |
24 |
|
1500 |
18 |
25 |
26 |
|
1620 |
20 |
27 |
28 |
|
1740 |
22 |
29 |
30 |
|
1860 |
23 |
31 |
33 |
|
1980 |
25 |
33 |
35 |
Dari percobaan pendeteksian frekuensi dengan algoritma Gortzel menggunakan processor DSP ini dapat disimpulkan beberapa hal.
-
1. Algoritma Gortzel dapat digunakan untuk mendeteksi frekuensi dimana tingkat keberhasilan pendeteksian sangat tergantung pada jumlah cuplikan (N), semakin banyak jumlah cuplikan maka semakin akurat pendeteksian frekuensi tersebut. Pada 50 kali percobaan, dengan jumlah N = 133 maka kesalahannya adalah 0.
-
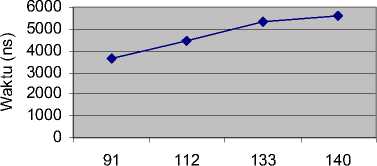
2. Semakin banyak jumlah N, maka proses iterasi yang dilakukan semakin banyak, sehingga waktu yang diperlukan untuk melakukan pendeteksian semakin lama. Untuk itu perlu dipilih jumlah N yang digunakan agar waktu yang diperlukan sesingkat mungkin.
[PRO96] Proakis, John G & Manolakis Dimitri G, “Digital Signal Processing”, Prentice Hall International, Inc, third edition, 1996.
[[SPRU163] “TMS320C3x DSP Starter Kit User’s Guide”, Texas Instruments Inc., Houston, 1996.
[LUD87] Ludeman, C Lonnie, “Fundamentals of Digital Signal Processing”, John Willey & Sons, Inc., 1987.
Gambar 2. Jumlah N vs. Kesalahan untuk 50 kali Percobaan
Grafik pengaruh jumlah N terhadap kecepatan proses perhitungan
Jumlah N
-
Gambar 3. Jumlah N vs. Kecepatan Proses Perhitungan
Teknologi Elektro
36
Vol.3 No.2 Juli – Desember 2004
Discussion and feedback