PERBANDINGAN PENGGUNAAN METODE OPTIMASI EXTENDED QUADRATIC INTERIOR POINT DENGAN NEURAL NETWORK UNTUK ECONOMIC DISPATCH PEMBANGKIT THERMAL DI BALI

Perbandingan Penggunaan Metode Optimasi …

Rukmi Sari Hartati, Sukerayasa

PERBANDINGAN PENGGUNAAN METODE OPTIMASI EXTENDED QUADRATIC INTERIOR POINT DENGAN NEURAL NETWORK UNTUK ECONOMIC DISPATCH PEMBANGKIT THERMAL DI BALI

Rukmi Sari Hartati, I Wayan Sukerayasa

Staf Pengajar Program Studi Teknik Elektro – Universitas Udayana

INTISARI

Makalah ini membahas alokasi pembebanan perbandingan penggunaan metode optimasi extended quadratic interior point dengan neural network untuk economic dispatch pembangkit termal di bali. Metode exstended quadratic interior point (EQIP) adalah metode deterministik yang merupakan pengembangan metode Karmakar oleh James A. Momoh dkk. dengan berdasarkan pada perbaikan kondisi awal sehingga bisa digunakan untuk menyelesaikan permasalahan pemrograman kuadratik (non linier). Metode jaringan Syaraf Tiruan model Hofield (HNN) adalah suatu metode kecerdasan buatan yang berdasarkan pada prinsip kerja jaringan saraf manusia, yang telah banyak digunakan sebagai metode alternatif untuk menyelesaikan permasalahan-permasalahan optimasi yang sulit dimana cara konvensional gagal untuk mencapai kecepatan, keakuratan atau efficiency. Dari hasil ujicoba pada sistem pembangkit termal dibali diperoleh hasil yang mendekati sama.

Kata kunci : Optimasi, extended quadratic interior point (EQIP), Jaringan saraf tiruan .

• 1.    Pendahuluan

Pemakaian Listrik secara komersiil sudah lebih dari seratus tahun yang lalu ( bulan januari di London dan bulan september 1882 di New York ). Sejak itu pemakaiannya terus meningkat. Tidak dapat dibantah bahwa listrik adalah bentuk energi yang saat ini merupakan penyokong kehidupan masyarakat yang sangat berarti; baik dari segi menunjang produktifitasnya, maupun unsur-unsur lain yang menyangkut kualitas hidupnya. Begitu besarnya peranan yang dimain kan oleh energi listrik ini maka konsekuensinya dituntut ketersediaan, kesinam bungan, dampak lingkungan yang bersih, kuantitas, dan kualitas yang tinggi, serta harga yang wajar

Dalam perencanaan, pengoperasian, dan pengontrolan sistem tenaga listrik muncul berbagai persoalan teknis maupun ekonomis, salah satunya diakibatkan oleh beban sistem yang dinamis. Di sisi lain energi listrik tidak dapat disimpan dalam jumlah banyak sehingga harus disediakan pada saat dibutuhkan oleh konsumen, akibatnya timbul persoalan dalam menghadapi kebutuhan daya listrik yang berubah dari waktu ke waktu. Apabila daya yang dikirim dari bus bus pembangkit lebih besar dari kebutuhan daya pada bus bus beban, maka akan timbul pemborosan daya. Sedangkan apabila daya yang dibangkitkan lebih rendah dari kebutuhan atau tidak memenuhi kebutuhan beban maka akan timbul pemadaman lokal pada bus bus beban, yang akan mengakibatkan kerugian pada konsumen.

Pada sistem pengoperasian tenaga listrik, komponen biaya operasi terbesar adalah biaya bahan bakar. Penghematan biaya bahan bakar dalam prosentase yang kecil akan memberi dampak yang besar dalam jumlah rupiah, mengingat besarnya jumlah biaya bahan bakar tersebut diatas. Oleh

karenanya efisien pemakaian bahan bakar sangat besar pengaruhnya terhadap penghematan biaya operasi.

Bali sangat terkenal sabagai salah satu tujuan wisata dunia, sampai saat ini sebagian pasokan tenaga listriknya masih tergantung dari Jawa melalui sistem interkoneksi Jawa-Bali lewat kabel laut yang hanya bisa dipakai dengan kapasitar sebesar 2 x 110 MW. Pembangkit yang beroperasi di Bali saat ini ada 9 unit PLTD dengan daya terpasang sebesar 65,7 MW, dan 4 unit PLTG dengan daya terpasang sebesar 125,5 MW, yang berlokasi di Pesanggaran. Satu unit PLTG berlokasi di Gilimanuk dengan daya terpasang sebesar 145 MW, yang merupakan pembangkit terbesar di Bali. Sehingga daya terpasang total setelah ditambah pasokan dari Jawa sebesar 556,2 MW, namun daya mampu sebesar 450 MW, hal ini disebabkan oleh derating kemampuan unit pembangkit. Beban puncak tertinggi mencapai 352 MW, pada tanggal 2 Oktober 2002. Apabila terjadi pemeliharaan unit pembangkit terbesar di Bali (145 MW), atau terganggunya kabel laut maka sistem kelistrikan di Bali akan mengalami kekurangan pasokan daya, sehingga akan terjadi giliran pemadaman listrik.

Upaya penanggulangan kekurangan daya sistem kelistrikan Bali, yang sudah dilakukan adalah penghematan daya di sisi pemakai (demand side management) yaitu dengan memasyarakatkan lampu hemat energi, sedangkan dari sisi suply yaitu menambah kapasitas pembangkitan. Disamping hal di atas penghematan biaya operasi terutama penghematan biaya bahan bakar sistem di Bali juga tidak kalah pentingnya untuk dilakukan. Salah satu bagian pengoperasian sistem tenaga listrik yang mengarah ke hal ini adalah penjadwalan pembangkitan daya secara ekonomis. Hal ini

merupakan suatu sistem untuk meminimumkan biaya operasi pada sistem tenaga listrik dengan cara mengoptimalkan pengalokasian pembang kitan daya antara generator-generator yang beroperasi pada sistem Bali serta menghasilkan suatu rencana operasi yang memenuhi persyaratan pengoperasian sistem tenaga listrik. Persyaratan tersebut terutama adalah daya yang dibangkitkan cukup untuk memasok beban dan rugi-rugi daya, tidak melanggar kendala sistem. Banyak teknik optimasi untuk pengalokasian pembangkitan daya antara generator-generator yang beroperasi agar optimal.

• 2.    Alokasi Pembebanan Ekonomis (Economic Dispatch)

Dalam sistem tenaga listrik, ada beberapa macam pembangkit tenaga (power plant), yaitu pembangkit tenaga thermal, pembangkit tenaga hidro, pembangkit tenaga nuklir dsb. Pembangkit thermal sendiri juga mempunyai beberapa perbedaan, sebagai contoh, perbedaan bahan bakar, harga maksimum dan minimum keluaran pembangkit, dsb. Salah satu karakteristik terpenting adalah biaya operasi. Biaya operasi masing-masing pembangkit berbeda, tidak hanya antar pembangkit, melainkan juga tergantung pada besarnya daya yang dibangkitkan. Dilain pihak, sistem tenaga listrik mempunyai beberapa pembangkit dengan karakteristik berbeda-beda. Dan pembangkit-pembangkit tersebut lokasinya jauh dari titik pusat beban, sehingga menyebabkan rugi-rugi transmisi yang besar, yang merupakan pengeluaran ekstra dari pembangkitan. Jadi, yang menjadi perhatian dalam hal ini adalah bagaimana menentukan jumlah daya yang harus dibangkitkan oleh masing-masing pembangkit dalam suatu sistem tenaga listrik sehingga dapat memenuhi jumlah kebutuhan beban dengan biaya minimum, dinamakan alokasi pembebanan ekonomis (Economic Load Dispatch).

Masalah alokasi pembebanan ekonomis dirumuskan untuk memperoleh kodisi optimal pembangkit dengan meminimalkan total biaya bahan bakar, yang dinyatakan sebagai [17,7,3]:

Biay^a _ operasi = i∑(a_i + ^bi^pGi + c_iP2 )

Rp/jam                      (1)

Kendala termasuk keseimbangan daya antara pembangkit dengan permintaan dan rugi-rugi daya [8]:

N

PD + PL = ∑ PG₁                 (2)

i=1

Penjadwalan daya aktif disyaratkan untuk memenuhi batas atas dan batas bawah pembangkit.

PGimin ≤ Pgi ≤ PG_imx              (3)

dengan

P_D    adalah total permintaan (MW)

P_L     adalah total rugi-rugi daya (MW)

P_Gi   adalah daya yang dibangkitkan oleh

pembangkit ke-i (MW)

a_i ,b_i ,c_i : Konstanta-konstanta pembangkit

P_Gimin : pembangkitan minimal unit i (MW)

P_{Gi max} : pembangkitan maksimal unit i (MW)

N : Jumlah unit pembangkit berputar

Beberapa metode yang telah berhasil digunakan untuk memecahkan permasalahan ini, baik metode konvensional dan kecerdasan buatan (artificial intelligent). Metode konvensional yang sudah dikenal antara lain metode Lagrange (Lagrangian Relaxation method), metode proyeksi gradien (gradient projection method), metode interior point, metode Generalize Reduce Gradient (GRG method), dsb. Metode optimasi dengan menggunakan Jaringan Syaraf Tiruan termasuk dalam metode kecerdasan buatan, dalam decade terakhir ini menjadi sangat penting dalam menyelesaikan permasalahan-permasalahan dalam sistem tenaga listrik, antara lain penjadualan unit-unit pembangkit (unit commitment), alokasi pembebanan ekonomis (economic load dispatch), peramalan beban (load forecasting), dsb.

• 3.    Metoda Optimasi Quadratic Interior Point

Metode Interior Point pertama diperkenalkan oleh Karmarkar adalah merupakan metode untuk menyelesaikan masalah pemrograman linier. Metode ini banyak digunakan dalam operasi penelitian (operation research) karena efisien, reliabel dan akurat. Metode ini kemudian dikembangkan oleh James A. Momoh dkk dengan berdasarkan pada perbaikan kondisi awal sehingga bisa digunakan untuk menyelesaikan permasalahan dengan pemrograman linier maupun kuadratik (non linier) yang dikenal dengan metode EQIP (Extended Quadratic Interior Point method). Yang paling penting dalam algoritma ini adalah titik start awal dapat ditentukan dahulu. Kemudian mencari solusi optimal dalam interior polytope yang didefinisikan oleh kendala-kendala sampai dicapai titik optimal. Dalam paper ini metode EQIP digunakan untuk menyelesaikan masalah optimasi alokasi pembebanan pada sistem kelistrikan Bali. Model quadratic interior point didefinisikan sebagai benkut [6, 10].

dengan

_ IrT' „

P = 21 XTQX + aT X                 (4)

min        max

b ≤ AX ≤ b

(5)

dimana :

X = variabel yang tidak diketahui (unknown) n-vektor

a = konstanta n-vektor

b^min,b^max = konstanta m-vektor

Q = matrik bujursangkar simetris

A = matriks koefisien mxn dengan m < n Programa linier dapat diperoleh dengan kasus khusus Q = 0.

Pada umumnya, dua m-vektor baru dibentuk yaitu S1 dan S2, dinamakan variabel slack, diperkenalkan untuk merubah kendala ketidaksamaan (5) menjadi bentuk persamaan :

permasalahan tidak mempunyai solusi atau solusinya menjadi tidak terbatas (unbounded).

Iterasi dimulai dengan suatu nilai awal yang

~0

memungkinkan X , algoritma proses optimasi menghasilkan nilai-nilai interior fisibel yang

~~  ~~

berurutan X , X ,........ X , X , ....sedemikian

sehingga

P = ¹ (X^~k+1)^TQ^~X^{~ k+1}+a^~TX^~k+1 < P =

k +12                                   k

1

(X^~k)^TQX ^k+a^~TX^k                      (14)

2

AX - S₁ = b ^miⁿ                    (6)

AX + S₂ = b ^max   S_bS₂ ≥ 0        (7)

Proses iterasi berhenti bila kriteria berhenti (stopping criterion) terpenuhi. Isi dari algoritma EQIP diberikan sebagai berikut:

~k                ~~ ~

Tentukan X sedemikian sehingga AX = b dengan ~k

X ≥ 0 untuk j = n+1,....,n+2m. Ketika kriteria ^j

berhenti tidak terpenuhi lakukan

sehingga bisa didefinisikan variabel baru :

f X y

X ∆

SS 1

IS 2 )

^,

Q∆l ^Qn×ⁿ

V⁰2m×n

0

n×2 m

On n

2 m×2 m

a ∆

a(nx1)

dan

_v ^a(2mx 1) ;

^,

min

^b(mx1)

= L^max

V b^{( mx} 1) )

b ∆

(8)

(9)

D_k :=diag[^~x₁^k,..., ^~x^kn+2m](15)

B := AD G_k : = QX ^k+ a(16)

KK

d : =D_tG_t w = ∖B B^t )1 B,d(17)

kk _{k kk} k_k

A ∆

A

(mxn)

V A (mxn)

I0

(mxm)   (mxm)

0/ I h ^χ

(mxm)    (mxm) )

(10)

dp := BTw - d(18)

kk k

γ: =min ∖dp^k ................,dp^k ]

L n + 1                 n + 2 m J

T:=(Dkdp^k)^T Q^~ (Dkdp^k)(20)

dengan I adalah matrik identitas mxm . Sehingga permasalahan optimasi quadratic (4) dan (5) mempunyai bentuk minimisasi sebagai :

min    P=₂¹X^TQX +a^~TX(11)

harus memenuhi kendala AX = b(12)

~

Xj ≥ 0, j = n+1, ... , n+2m(13)

β1 : =

β2 : =

1

, γ < 0,

^γ

kt k

(dp ) dp

T

β2 : = 10⁶, T ≤ 0

β1: = 10⁶, γ ≥ 0

, T > 0, ...................

(22)

(21)

β := min [β₁, β2],    d := Ddpk            (23)

xk

Masalah optimasasi quadratik yang diperlihatkan pada (11) - (13) di atas dengan mengasumsikan memiliki batas titik awal (bounded ~o

interior point) X . Jika tidak demikian maka

X ^{k + 1} := X ^k + β                      (24)

x

set k : = k+1, dimana k adalah jumlah iterasi.

Kriteria berhenti adalah perubahan relatif fungsi objektif pada setiap iterasi, yaitu

|Pk+1–Pk|/max{1,|Pk|} < є

atau perubahan relatif pada nilai interior yang memungkinkan pada setiap iterasinya

|X^~k+1-X^~k| < є

Untuk menjaga solusi dari masalah pada setiap iterasi agar selalu berada dalam daerah interior yang memungkinkan, algoritma EQIP memerlukan perhitungan dari nilai start awal titik interior yang ~     ~~   ^~

fisibel X yaitu AX = b dengan ~ ≥ 0 untuk j = ^j

n+1,....,n+2m.

Nilai awal yang memungkinkan dapat dihasilkan dengan memperkenalkan variabel buatan xs. EQIP akan menghasilkan nilai yang memungkinkan dengan meminimalkan x [11]: s

Minimize[xs](25)

Harus memenuhi kendala

~~~

AX +(b - Ae)x_s=b(26)

Hopfield (Hopfield Neural Network / HNN ) banyak digunakan dalam penelitian tentang alokasi pembebanan ekonomis. Metode ini akan diaplikasikan untuk menyelesaikan alokasi pembebanan untuk sistem kelistrikan Bali.

Dengan mengaplikasikan Hopfield Neural Network berdasarkan pada persamaan syaraf tiruan dinamis berikut:

dU

ⁱ

dt ^jVj +i

(28)

U_i adalah total input dari syaraf (neuron) i , dapat dinyatakan sebagai:

Ur = _l ∑_j TjVj ⁺ Ii

(29)

dengan

T_ij = bobot hubungan antara syaraf j dan syaraf i

I_i = ambang batas (threshold) neuron i

V_i adalah output dari syaraf i , dapat dinyatakan sebagai fungsi U_i sebagai V_i = g U_i) dengan g Ui) adalah fungsi tak linier pada syaraf yang merupakan fungsi sigmoid yang dinyatakan sebagai [2]:

~ ≥ Ountuk j = n+1,....,n+2m. x_s≥0          (27)

j

g (U_i) = (1 + tanh(λ Ui )/2               (30)

dengan e=(1,1,....,1)^T.

Sehingga bisa disimpulkan bahwa aplikasi dari EQIP meliputi :

~~     ~

• 1.    Formulasi matrik A, Q, a dan b dalam fungsi

objektif kuadratik dengan kendala linear.

• 2.    Menghitung nilai awal interior yang memungkinkan dari persamaan (25 – 27).

• 3.    Eksekusi algoritma EQIP hingga kriteria berhenti terpenuhi.

• 4.    Metode Optimasi Jaringan Syaraf Tiruan Model Hopfield (HNN)

Jaringan Syaraf Tiruan (Artificial neural networks) telah dipromosikan sebagai metode alternatif untuk menyelesaikan permasalahan-permasalahan sistem tenaga yang sulit dimana cara konvensional gagal untuk mencapai kecepatan, keakuratan atau efficiency [9]. Metode optimisasi dengan menggunakan Jaringan Syaraf Tiruan model

dengan λ adalah suatu konstanta

Fungsi sigmoid tersebut sebagai fungsi masukan keluaran dengan harga 0 atau 1 sebagai keluaran. Fungsi sigmoid ini merupakan fungsi monoton naik dalam batasan V .

Energi E dari didefinisikan sebagai [8]:

E(V)=--5∑∑TijViVj -∑IiVi             (31)

ij         i

Energi menunjukkan suatu status seberapa baik jaringan (network) tersebut memenuhi kendala pada permasalahan dimana jaringan didesain. Hal terpenting dalam menyelesaikan masalah optimasi adalah memformulasikan perhitungan yang sesuai untuk fungsi energi E(V) sehingga menghasilkan energi terendah yang akan menghasilkan nilai V yang optimal. Aplikasi metode ini untuk menyelesaikan masalah optimasi dapat dijelasakan sebagai berikut.

Secara umum disini dijelaskan tentang permasalahan non-linear programming [5]:

Meminimumkan f (x) = 12 xtPx + q^tx

(32)

Kendala

t

gi^x = si

t

^wi^x ≤ di

i = 1........n

or

wix ≥ di        i = 1.....m

Pertama, abaikan dulu kendala ketidaksamaan, kemudian dilakukan mapping ke Hopfield Neural Network Hubungkan variable x ke neuron output v dan fungsi energi berikut konvergen ke harga minimum [9]:

E = αF (v) + ∑ β_i[β_i (v )]2                 (33)

Disini fungsi F(v) dan G(v) menyatakan fungsi tujuan dan kendala kesamaan dan harus memenuhi beberapa kondisi yang disyaratkan oleh fungsi energi. Kendala kesamaan dihitung dengan menambahkan [ G(v) ]² ke E agar supaya minimisasi mismatch ke nol, kalau tidak solusi yang dihasilkan bisa terjadi kekurangan daya pembangkitan. Koefisien positif α dan β digunakan untuk menghitung derajad kepentingan relatif (bobot) dari fungsi kendala dan tujuan. Fungsi energi terdiri dari m kendala kesamaan yang ditambahkan ke fungsi tujuan, dan solusi konvergen bisa tidak merupakan global optimum.

Pemodelan alokasi pembebanan ekonomis dinyatakan dalam bentuk fungsi energi dalam Jaringan Syaraf Tiruan (Neural Network) sebagai:

(              } 2

E = (A / 2) I PD + PL - ∑ P_i I

k i J

+ (B / 2) ∑(a_i + b Pi + Ci P² )

i

(34)

Dengan A, dan B adalah faktor bobot (weight). Daya keluaran P_i dapat dinyatakan sebagai

Pi= gi (Ui )

Sehingga diperoleh hasil pemetaan dari alokasi pembebanan ekonomis ke jaringan syaraf tiruan dengan membandingkan koefisien-koefisien dari persamaan (1) dan (2) dengan persamaan (31), dan dengan menyatakan V_i sebagai P_i , diperoleh

Tii =- A — BCi

Tij = — A                                    (35)

Ii = A(PD + Pl ) - .5Bbi

Untuk menyelesaikan kendala ketidaksamaan, ada beberapa cara, diantaranya dengan menggunakan variable tambahan (slack variable). Disini kendala ketidaksamaan diselesaikan dengan memodifikasi fungsi sigmoid sebagai berikut :

^gi ^(Ui⁾ = ^(Pi max ^- Pi min ⁾

(36)

(1 + tanh( λU_i))∕2 + P_imin

Sehingga proses perhitungan menjadi :

∆ U i = {∑Tj + I_i }∆ t

= {^-A⁽j^Pj ^{- p}D ^{- p}l ) ^{- b(a}iPi ^{+ b}i ∕²M^{δt (37)}

Pi= gi (Ui)                                 (38)

= (Pimax — Pimin )(¹ + t^Ui))/ ² + Pimin

• 5.    Simulasi

Untuk penelitian ini diambil sampel pembebanan pembangkit berdasarkan pemakaian beban yang tercatat pada data PT. INDONESIA POWER UBP BALI pada tanggal 31 Desember 2003 pada pukul 18.00-22.00.

Saat sampel pembebanan diambil PLTG Gilimanuk dalam kondisi pemeliharaan rutin. Penjadwalan dilakukan hanya untuk pembangkit di Bali saja dengan asumsi bahwa beban yang ditanggung dalam penjadwalan ini adalah beban yang sebenarnya dikurangai pasokan dari Jawa. Beban dimaksud adalah beban pada bus pembangkit, sehingga dalam perhitungan tidak mengikutkan rugi rugi transmisi.

Berdasarkan data performance test sesudah inspection sentral PLTD dan PLTG Pesanggaran, kemudian dicari karakteristik input-output hanya pada unit-unit PLTD dan PLTG yang beroperasi dengan menggunakan metode regresi least square. Karakteristik Input-Output PLTD dan PLTG seperti dalam tabel 1.

Pembebanan pembangkit hasil simulasi dengan kedua metode telihat pada tabel 2.

Tabel 1: Karakteristik input-output pembangkit

No	Unit	Pimin (MW)	Pimaks (MW)	Konstanta pembangkit
				ai (Rp/MW2h)	bi (Rp/MWh)	ci (Rp/h)
1	PLTD-2	1,27	4,6	24874	332018	151525
2	PLTD-4	1,27	4,5	40150	263435	168869
3	PLTD-5	1,05	3,5	15056	365241	150111
4	PLTD-6	1,70	5,3	2248,4	430632	50789
5	PLTD-7	1,70	5,6	2344,9	444215	69563
6	PLTD-8	1,60	4,5	665,64	486647	85280
7	PLTD-9	1,60	4,5	3396	465586	125127
8	PLTD-10	3,00	10,5	835,46	281901	998167
9	PLTD-11	3,80	10,5	21889	10387	1761574
10	PLTG-1	5,00	19,4	6332	41009	9916321
11	PLTG-2	5,00	19,8	12672	324837	3318182
12	PLTG-3	10,00	39,5	1046	326584	7520323
13	PLTG-4	10,50	35	5779	177322	8907942
14	PLTG-Gilimanuk	40	129	1869	21993	34862722
Fi(Pi) =	aiPi 2 + biPi + ci

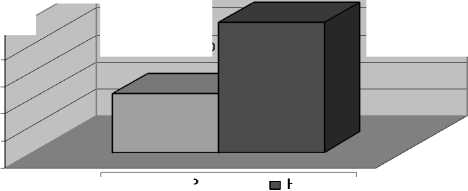
Tabel 2 Perbandingan hasil pembebanan metode EQIP dengan HNN

Total biaya

HNN, 433,815,909

EQIP, 431,176,790

434,000,000

433,000,000

432,000,000

431,000,000

430,000,000

429,000,000

I■ EQIP

HNN

UNIT	Pukul
	18.00		19.00		20.00		21.00		22.00
	EQIP	HNN	EQIP	HNN	EQIP	HNN	EQIP	HNN	EQIP	HNN
PLTD-2 (MW)	4,438	3,662	4,600	4,600	4,600	4,600	4,600	4,600	4,600	4,600
PLTD-4 (MW)	4,459	3,123	4,500	3,722	4,500	3,713	4,500	3,650	4,500	3,596
PLTD-5 (MW)	3,500	3,500	3,500	3,500	3,500	3,500	3,500	3,500	3,500	3,500
PLTD-6 (MW)	5,225	5,300	5,300	5,300	5,300	5,300	5,300	5,300	5,300	5,300
PLTD-7 (MW)	1,700	5,600	5,600	5,600	5,600	5,600	5,600	5,600	5,600	5,600
PLTD-8 (MW)	1,600	4,500	1,600	4,500	1,600	4,500	1,600	4,500	1,600	4,500
PLTD-9 (MW)	1,600	4,500	2,518	4,500	2,440	4,500	1,887	4,500	1,600	4,500
PLTD-10 (MW)	10,500	10,500	10,500	10,500	10,500	10,500	10,500	10,500	10,500	10,500
PLTD-11 (MW)	10,500	10,500	10,500	10,500	10,500	10,500	10,500	10,500	10,500	10,500
PLTG-1 (MW)	19,400	19,400	19,400	19,400	19,400	19,400	19,400	19,400	19,400	19,400
PLTG-2 (MW)	19,279	7,471	11,782	9,370	11,761	9,341	11,613	9,142	11,300	8,971
PLTG-3 (MW)	39,500	39,500	39,500	39,500	39,500	39,500	39,500	39,500	39,500	39,500
PLTG-4 (MW)	35,000	29,144	35,000	33,308	35,000	33,246	35,000	32,808	35,000	32,433
TOTAL (MW)	146,700	146,700	154,300	154,300	154,200	154,200	153,500	153,500	152,900	152,900
Beban (MW)	146,700	146,700	154,300	154,300	154,200	154,200	153,500	153,500	152,900	152,900

Gambar 1. Perbandingan total biaya

• 6.    Kesimpulan

Hasil pembebanan pembangkit selama lima jam menunjukkan bahwa kedua metode mem perlihatkan konsistensinya untuk tidak melanggar kendala dan memenuhi beban yang dibutuhkan.

Total biaya pembebanan selama lima jam, untuk metode EQIP lebih murah 0,6 % dari metode HNN.

• 7.    Daftar Pustaka

• [1]    Abe, Shigeo dkk., Solving Inequality Constrained Combinatorial Optimization Problems by the Hopfield Neural Networks, Neural Networks, Vol.5, pp. 663-670, 1992.

• [2]    Burchett, R.C., dkk., Developments in Optimal Power Flow, IEEE Transactions on Power Systems 1982, PAS-101, pp. 406-414.

• [3]    Duncan J. Glover and Mulukutla Sarma, Power System Analysis and Design: With Personal Computer Application, PWS-KENT Publishing Co., Boston, 1989.

• [4]    ommel, H.W. , and Tinney, W.F. , Optimal Power Flow Solutions, IEEE Transactions on Power Systems 1968, PAS-87, pp. 1866-1876.

• [5]    El-Hawary, M.E., Applications of artificial neural networks in electric power systems operational planning, Engineering Intelligent Systems, Vol. 7, no. 1, March 1999.

• [6]    Eiselt, H.A., G. Pederzoli, C.L.Sandblom, Continuous Optimization Models, Walter de Gruyter, Berlin, New York, 1987.

• [7]    Hadi Saadat, Power System Analysis, WCB McGraw-Hill Companies, New York, 1999.

• [8]    Park, J.H., dkk., Economic Load Dispatch for Piecewise Quadratic Cost Function Using Hopfield neural Networks, IEEE Transactions on Power Systems, Vol. 8, No. 3, August 1993.

• [9]    Lee, K.Y., Y.M Park, J.L.Ortiz, Fuel-cost minimization for both real-and reactive-power dispatches, IEE Proceedings, Vol. 131, Pt. C, No.3, May 1984.

• [10]    Momoh, J.A dkk., The Quadratic Interior Point Method Solving Power System Optimization Problems, IEEE Transactions on Power Systems, Vol. 9, No. 3, August 1994.

• [11]    Momoh, J.A dkk, Extension of The Interior Point Method, EPRI Proceeding1991, Advanced Maths for Power Systems, San Diego CA.

• [12]    Rosen, J.B., The Gradient Projection method for non-linear programming-Part I ‘Linear constraints, J. Soc. Indust. Appl. Math., 1960,3,pp. 181-217.

• [13]    Rukmi Sari Hartati & El-Hawary, M.E., Summary of Application of Hopfield Neural Network to Economic Load  Dispatch,

Proceeding of Canadian Conference of Electrical and Computer Engineering, Halifax, May 2000.

• [14]    Rukmi Sari Hartati, El-Hawary, M.E., New Approach for solving Optimization Problems in Economic Load Dispatch using Hopfield Neural Networks, Proceedings of CCECE 2000, May 710, 2000.

• [15]    Salgado, R. A. Bramaller, P. Aitchison, Optimal Power Flow solutions using the gradient projection method, part 1 and 2, IEE Proceedings, Vol. 137, Pt. C. No. 6, November 1990.

• [16]    Simon Haykin, Neural Networks, a comprehensive foundation, Second edition, Prentice Hall, Upper Saddle River, New Jersey, 1999.

• [17]    Sukerayasa, Rukmi Sari Hartati, Aplikasi Metode Optimasi Exstended Quadratic Interior dan Gradient Projection untuk Economik Dispatch Pembangkit Termal di Bali, Majalah Ilmiah Teknologi Elektro, Vol. 2 No. 2 Juli-Desember 2003, ISSN: 1693-2951.

• [18]    Wood, A.J. and Wollenberg, B.F, Power generation, operation, and control, Second edition, John Wiley & Sons New York, 1996.

Teknologi Elektro

32

Vol.3 No.2 Juli – Desember 2004