Jurnal Matematika Vol. 12, No.1, Juni 2022, pp. 11-19

Article DOI: 10.24843/JMAT.2022.v12.i01.p145

ISSN: 1693-1394

Pemodelan Lama Sekolah

di Kabupaten Gianyar dengan Pendekatan MARS

Luh Putu Safitri Pratiwi

Program Studi Sistem Informasi, Institut Teknologi dan Bisnis Stikom Bali e-mail: [email protected]

Abstract: MARS does not provide an assumption of a relationship between response variables and predictors, and is flexible in functional form. This study aims to obtain a model of the average length of schooling and want to know the factors that affect the length of schooling in Gianyar Regency. In selecting the best MARS model, a trial and error process is used to obtain the minimum GCV model. The results obtained by the MARS analysis with a GCV of 0.950 resulted in a combination of BF = 48, MO = 2 and MI = 3. The form of the equation

  • Yˆ= 7.836596+ 0.4805948 *BF - 0.6325919 *BF - 0.2208233 *BF .

With factors affecting the length of school, namely HDI (Human Development Index), RT expenditure per capita (thousands of rupiah), and AMH (literacy rate).

Keywords: GCV, lama sekolah, MARS

Abstrak: MARS tidak memberikan asumsi hubungan antara variabel respon dan prediktor, serta bersifat fleksibel dalam bentuk fungsional. Penelitian ini bertujuan mendapatkan model rata-rata lama sekolah dan ingin diketahui faktor-faktor yang mempengaruhi lama sekolah di Kabupaten Gianyar. Dalam pemilihan model MARS terbaik, digunakan proses trial and error hingga didapatkan model GCV minimum. Hasil yang diperoleh analisis MARS dengan GCV sebesar 0.950 menghasilkan kombinasi BF = 48, MO = 2 dan MI = 3. Bentuk persamaan

  • Yˆ= 7.836596+ 0.4805948 *BF - 0.6325919 *BF - 0.2208233 *BF .

Dengan faktor yang mempengaruhi lama sekolah yaitu IPM (Indeks Pembangunan Manusia), pengeluaran RT perkapita (ribu rupiah), dan AMH ( Angka Melek Huruf).

Kata Kunci: GCV, lama sekolah, MARS

  • 1.    Pendahuluan

Seseorang yang memiliki pendidikan tinggi memiliki peluang diterima pada suatu perusahaan akan semakin besar. Capaian rata-rata lama sekolah akan semakin tinggi apabila seseorang memiliki tingkat pendidikan yang tinggi (Widiatma, 2012). Beberapa kabupaten di Bali khususnya Kabupaten Gianyar rata-rata lama sekolah di tahun 2019 yakni sebesar 8,94 meningkat sebesar 9,04. Walaupun mengalami peningkatan,

pemerintah Kabupaten Gianyar tetap berupaya agar nilai dari rata-rata lama sekolah meningkat. Salah satu langkah yang dilakukan untuk meningkatkan rata-rata lama sekolah hingga mencapai target dari IPM Indonesia atau bahkan lebih tinggi serta dapat memberikan rekomendasi terhadap perbaikan mutu kurikulum ataupun metode pendidikan yaitu dapat dilakukan dengan melihat faktor-faktor yang berpengaruh terhadap rata-rata lama sekolahnya dengan menggunakan pendekatan MARS (Multivariate Adaptive Regression Spline). MARS masuk ke dalam keluarga regresi nonparametrik, dikarenakan tidak mengasumsikan bentuk hubungan fungsional antara variabel respon dan prediktor, dan fleksibel (Munoz dan Felicimo, 2004 dalam Jalaluddin, 2009).

Terdapat beberapa penelitian yang mengkaji mengenai penerapan rata-rata lama sekolah di Indonesia. Penelitian mengenai rata-rata lama sekolah pernah diteliti oleh Siskawati (2021) meneliti pengaruh rata-rata lama sekolah yang mempunyai pengaruh yang signifikan terhadap variabel tingkat pengangguran terbuka. Nitivijaya (2016) membagi beberapa varibel prediktor yang berpengaruh terhadap rata-rata lama sekolah dengan skala nominal, ordinal dan rasio. Adapun variabel prediktor ysng dimaksud jenis kelamin, status bekerja, status perkawinan, tingkat pendidikan kepala RT, jumlah ART, rata-rata pengeluaran RT perkapita sebulan (juta). Sedangkan Diana (2019) melakukan pemodelan rata-rata lama sekolah di Kabupaten Padang Pariaman dengan data jumlah SLTA, rata-rata jarak terhadap sekolah, dan persentase keluarga yang bekerja di bidang pertanian. Amanah (2021) berpendapat dalam penelitiannya bahwa rata-rata lama sekolah memiliki hubungan positif serta signifikan terhadap IPM, disamping berpengaruh terhadap IPM, rata-rata lama sekolah juga berpengaruh terhadap kemiskinan (Faritz dan Soejoto, 2020; Pradipta dan Dewi, 2020) serta dipengaruhi oleh angka putus sekolah (Sabrina, 2022).

Berdasarkan penelitian yang telah diuraikan, maka penelitian ini mengkaji pemodelan MARS dengan metode GCV yang diaplikasikan pada data lama sekolah di Kabupaten Gianyar.

  • 2.    Metode Penelitian

    2.1    Multivariate Adaptive Regression Spline (MARS)

MARS merupakan salah satu pendekatan regresi nonparametrik yang dikembangkan oleh Friedman (1991). Metode MARS sering digunakan di bidang ilmu komputer salah satunya jaringan syaraf tiruan (Hastie dan Tibshirani, 1990). Semua metode tersebut memiliki tujuan untuk menentukan model estimasi terbaik terhadap fungsi sesungguhnya. Metode ini merupakan pengembangan dari pendekatan Recursive Partioning Regression (RPR). Salah satu kelemahan RPR yaitu model yang dihasilkan tidak kontinu pada knot.

Salah satu kegunaaan MARS adalah untuk mengatasi kelemahan model RPR yang artinya diperoleh model kontinu pada knot (Hastie, 1990). Hal ini dilakukan untuk mengatasi keterbatasan RPR, antara lain menghasilkan fungsi basis menjadi :

Km

Bm (x) = ∏[skm ' (xv(k,m) - tkm )]+.

k=1

Kurva f (x) diperoleh melalui Penalized Least Square (PLS), yaitu kegunaannya untuk meminimumkan Persamaan (1): _n_                       b,2

Estimator model MARS dapat ditulis seperti Persamaan (2): MK

m =1

dengan

a0     = konstanta

M    = jumlah fungsi basis

K     = derajat interaksi

χv (k, m) = variabel prediktor

tkm     = nilai knot dari variabel prediktor xv(k,m)

Dengan menggunakan Persamaan (2), maka model MARS adalah : MKm

m=1     k=1

dengan, Bm (x) = ∏ [ Skm ■(Xv(k,m)  tkm )]■

k=1

  • 2.2 Metode Pemilihan Titik Knot yanng Optimal

Pemilihan titik knot optimal dalam regresi Spline truncated pada umumnya didasarkan pada metode Generalized Cross-Validation (GCV) (Wu &Zhang, 2006). Secara umum GCV didefinisikan:

1N

∑[ y- fM(xi)]2

LOF (. f m ) =


N i=1_________________

(4)


2

1 - C (M)

N

dengan:

dimana:

LOF = loss of function merupakan GCV minimum

C(M) = Trace[B(BTB)-1BT]+1 merupakan banyaknya parameter yang akan diestimasi ~

C (M) = C(M)+d.M ,dimana nilai d terbaik terdapat didalam batasan 2 ≤ d ≤ 4.

  • 2.3 Jenis dan Sumber Data

Data yang digunakan bersumber dari SUSENAS di Direktorat Diseminasi Statistik BPS Kabupaten Gianyar. Data memuat informasi tentang lama sekolah dan faktor-faktor yang mempengaruhi lama sekolah, dimana akan digunakan sebagai variabel penelitian.

Adapun gambaran umum variabel penelitian yang digunakan sebagai berikut:

  • a.  Y Lama Sekolah Penduduk Usia Sekolah

  • b.  Variabel prediktornya

  • X1  IPM (Indeks Pembangunan Manusia)

X2  Tingkat Pengangguran Terbuka (TPT)

X3

Penduduk Bekerja Menurut Lapangan Usaha sektor primer pertanian

X4  Pengeluaran RT perkapita (ribu rupiah)

X5  Persentase penduduk miskin

X6  Angka partisipasi sekolah

X7  APS (angka putus sekolah)

X8  Angkatan kerja 15+ yang bekerja

X9  Bukan angkatan kerja yang sekolah

X10 Banyaknya Guru Sekolah

  • X11  AMH (Angka Melek Huruf)

X12 Banyaknya Sekolah Menengah

Langkah-langkah dalam penelitian ini adalah:

  • 1.   Mengambil data SUSENAS di Direktorat Diseminasi Statistik BPS.

  • 2.    Mengumpulkan data keseluruhan variabel yang digunakan dalam pembentukan model.

  • 3.    Sebelum dilakukan pengolahan data, terlebih dahulu dilakukan pem-plot-an data variabel respon dengan setiap variabel-variabel prediktornya.

Untuk mendapatkan model lama sekolah di Kabupaten Gianyar dengan pendekatan MARS, diberikan Langkah- Langkah sebagai berikut:

  • 1.    Untuk memilih model terbaik digunakan proses trial and error hingga didapatkan

model GCV minimum. Langkah-langkahnya sebagai berikut:

  • a.   Memilih maksimum fungsi basis

  • b.   Memilih jumlah maksimum interaksi

  • c.    Setiap knot dipilih minimal jumlah pengamatan

  • 2.    Memperoleh hasil estimasi parameter.

  • 3.    Mendapatkan model terbaik dengan kriteria seperti pada langkah 1.

  • 4.    Memperoleh variabel yang memiliki pengaruh signifikan

  • 3.    Hasil dan Pembahasan

Scatterplot menunjukkan baik di variabel prediktor dengan variabel respon menunjukkan pola yang sulit diketahui hubungan antar variabel. Selain itu, dalam setiap variabel memiliki karakteristik yang berbeda tiap tahun, sehingga variabel prediktor tidak mampu dijelaskan menggunakan analisis deskriptif (Gambar 1). Ketidakjelasan pola hubungan ini maka digunakan pendekatan regresi nonparametrik dengan metode MARS.

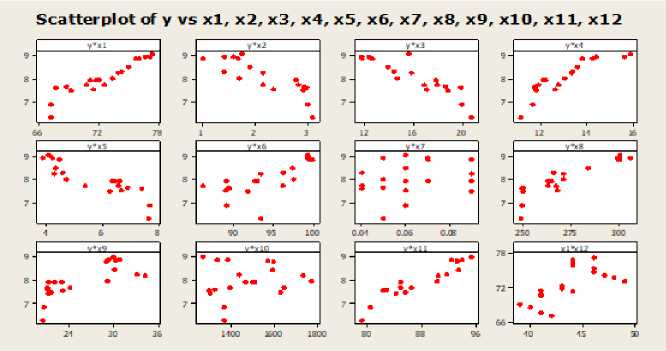
Gambar 1. Scatterplot Variabel Respon dengan Prediktor

  • 3.1    Multivariate Adaptive Regression Spline

Dalam penelitian ini, penulis menentukan fungsi basis 24, 36 dan 48, sesuai dengan Friedman (1991), yang menyarankan batasan fungsi basis antara 2- 4 kali banyaknya jumlah prediktor yaitu 12. Jumlah variabel prediktor dalam penelitian ini sebanyak 12 variabel. Sedangkan interaksi variabel yang ditentukan 1, 2 dan 3, serta minimum observasinya minimum jumlah pengamatan (MO) yaitu sebesar 0, 1, 2, dan 3. Nilai minimal observasi dicobakan dengan berbagai nilai kemungkinan, namun pada titik-titik tersebut diperoleh nilai GCV minimum. Pada tahap awal pembentukan model, dilakukan

kombinasi model dengan menentukan maksimum (BF) 24, 36 dan 48 maksimum interaksi (MI) 1, 2 dan 3 serta MO setiap knot sebesar 0, 1, 2, dan 3. Berikut hasil pemodelan BF, MI, dan MO pada Tabel 1.

Tabel 1. Hasil Pemodelan BF = 48, dan Kombinasi Nilai MI dan MO

BF

MO

MI

GCV

R-Square

(1)

(2)

(3)

(4)

(5)

1

0.565

0.794

48

0

2

0.505

0.729

3

0.513

0.745

1

0.709

0.476

48

1

2

0.686

0.674

3

0.735

0.418

1

0.511

0.741

48

2

2

0,345

0.949

3

0.340

0.950

1

0.400

0.900

48

3

2

0.401

0.899

3

0.435

0.811

Selanjutnya jika basis fungsi diperbesar BF = 48, terlihat hasil pengolahan pada Tabel 1. Dari hasil pengolahan terlihat bahwa nilai GCV sangat bervariasi untuk setiap kombinasi nilai MO dan MI yang berbeda. Nilai GCV minimum pada pengolahan BF=48 diperoleh pada saat MO=2 dan MI = 3 yaitu sebesar 0.340, dengan nilai R2 = 0.950. Berdasarkan parsimoni model dalam MARS yaitu didasarkan pada nilai GCV minimum maka model yang dihasilkan oleh kombinasi ini merupakan model yang terbaik untuk menerangkan hubungan antara lama sekolah dengan variabel-variabel prediktornya. Model pada kombinasi ini, menghasilkan nilai GCV = 0.340 dan R2 = 0.950,

Hasil pemilihan model terbaik pada rata-rata lama sekolah di Kabupaten Gianyar didapat kombinasi BF = 48, MO = 2 dan MI = 3 dengan nilai GCV terkecil adalah 0,340 dan model sebagai berikut

  • Yˆ= 7.836596+ 0.4805948 *BF - 0.6325919 *BF - 0.2208233 *BF

dengan

BF = max(0,X - 71.66)

BF = max(0,X - 12.122)

BF = max(0,85 - X )

Dari Persamaan di atas akan dilakukan proses eliminasi setelah fungsi basis digunakan. Terdapat empat fungsi basis yaitu, fungsi basis awal yaitu fungsi basis induk bernilai 7.836596. Selanjutnya, koefisien fungsi basis yang pertama bernilai 0,4805948. Hal ini berarti setiap perubahan fungsi basis satu satuan akan menaikkan nilai rata-rata lama sekolah di Kabupaten Gianyar sebesar 0,4805948 pada daerah dengan nilai baku IPM lebih dari 71,66. Nilai koefisien fungsi basis kedua yaitu -0,6325919 artinya setiap perubahan fungsi basis kedua satu satuan akan menurunkan nilai rata-rata lama sekolah sebesar 0,6325919 kali dari nilai fungsi basis. Pada daerah dengan nilai baku pengeluaran RT perkapita (ribu rupiah) lebih dari 12,122. Fungsi basis ketiga mempunyai koefisien -0,2208233 artinya setiap penurunan fungsi basis ketiga satu satuan akan menurunkan nilai rata-rata lama sekolah sebesar 0,2208233 kali. Pada daerah dengan nilai baku AMH kurang dari 0,85.

Sehingga variabel prediktor yangmempunyai pengaruh signifikan terhadap kasus rata-rata lama sekolah adalah (X1) IPM, (X4) pengeluaran RT perkapita (ribu rupiah), dan (X11), AMH.

  • 4.1    Kesimpulan

Hasil pemilihan model terbaik pada   rata-rata   lama sekolah di

Kabupaten Gianyar didapat kombinasi BF = 48, MO = 2 dan MI = 3 dengan model

  • Yˆ= 7.836596+ 0.4805948 *BF - 0.6325919 *BF - 0.2208233 *BF

dengan GCV minimum sebesar 0,340 dan variabel yang mempengaruhi kasus rata-rata lama sekolah adalah (X1) IPM, (X4) pengeluaran RT perkapita (ribu rupiah), dan (X11) AMH.

  • 4.2    Saran

Untuk penelitian selanjutnya perlu memasukkan variabel lain yang lebih bisa menjelaskan rata-rata lama sekolah yaitu menambah variabel-variabel sosial ekonomi lainnya.

Ucapan Terima Kasih

Ucapan terima kasih kepada ITB STIKOM Bali yang telah memberi dukungan pendanaan terhadap penelitian ini sehingga dapat diselesaikan dengan baik.

Daftar Pustaka

Amanah, S. (2021). Pengaruh Angka harapan Hidup, Harapan Lama Sekolah, Rata-Rata Lama Sekolah dan Pengeluaran per Kapita Terhadap Indeks Pembangunan Manusia di Provinsi Sumatera Barat. Sumatera Barat :Tugas Akhir, Universitas Andalas.

BPS Gianyar. (2020). Indeks Pembangunan Manusia (IPM) Kabupaten Gianyar Tahun 2020, BPS Kabupaten Gianyar

Diana, R. dan Rory. (2019). Estimasi Rata-Rata Lama Sekolah Tingkat Kecamatan di Kabupaten Padang Pariaman Dengan Metode Empirical Best Linear Unbiased Predictor. Seminar Nasional Official Statistics 2019: Pengembangan Official Statistics dalam mendukung Implementasi SDG’s.

Faritz, M., N. dan Soejoto, A. (2020). Pengaruh Pertumbuhan Ekonomi danRata-rata Lama Sekolah terhadap Kemiskinan di Provinsi Jawa Tengah. Surabaya. Jurnal Pendidikan Ekonomi Universitas Negeri Surabaya, Vol 08 No 01.

Friedman, J.H. (1991). Multivariate     Adaptive Regression Splines (with Dis

cussion), The Annals of Statistics, Vol 19, No 1, hal. 1-141.

Hastie, T., Tibshirani, R. (1990). GeneralizedAdditive Models. London: Chapman & Hall

Hastie, T., Tibshirani, R., dan Friedman, J.H. (2001). The Element of Statistical Learning: Data Mining, Inference, and Prediction. Springer series in Statistics, New York

Jalaluddin, M. (2009). Pemodelan Partisipasi Anak dalam Kegiatan Ekonomi di Sumatera Barat Menggunakan Regresi Logistik dan MARS. Surabaya: Tesis, Institut Teknologi Sepuluh Nopember.

Nitivijaya, M., Iriawan, N. dan Kuswanto, H. (2016). Pemodelan Angka Lama Sekolah Di Provinsi Papua Barat Dengan Pendekatan Model Mixture Survival Bayesian. Surabaya: Tugas Akhir, Institut Teknologi Sepuluh Nopember

Widiatma, N. (2012). Analisis Pengaruh PDRB,Agrishare,Rata-Rata Lama Sekolah dan Angka Melek Huruf terhadap Jumlah Penduduk Miskin di Indonesia. Semarang : Skripsi, Universitas Diponegoro.

Pradipta, S., A. dan Dewi, R., M. (2020). Pengaruh Rata- Rata Lama Sekolah Dan Pengangguran Terbuka Terhadap Kemiskinan, JUPE Vol 08 No 03, 109 -115.

Sabrina,R., Manurung, A. I., dan Sirait, B. A. (2022). Peningkatan Rata-Rata Lama Sekolah (RLS) dari Harapan Lama Sekolah (HLS) di Sumatera Utara. Jurnal Pendidikan Tambusai, Vol 6 No 1, 4784-4792

Siskawati, N., Surya, R.Z., dan Sudeska, E. (2021). Pengaruh Harapan Lama Sekolah, Rata – Rata Lama Sekolah Terhadap Tingkat Pengangguran Terbuka Di Kabupaten / Kota Provinsi Riau. Jurnal Selodang Mayang, 7(3), 173-177.

Wu, H. & Zhang, J. T. (2006). Nonparametric Regression Methods for Longitudinal Data Analysis. New York: John Wiley and Sons, Inc.

19